2019年前三季度江西城市经济发展能力分析

(江西农业大学 江西 南昌 330000)

经济发展一直都离不开四个必要条件：人口、产业、资源和交通，江西省作为一个有4600万人口的中部省份，坐拥中国最大的淡水湖鄱阳湖，周边地区多为山区、中部多为丘陵平原，在历史上就被当成是“鱼米之乡”，江西的地下贮藏着大量矿产资源和稀有金属，在近代工业起步时期发挥了重大作用，这些也带动了江西的经济发展。随着中部崛起战略的实施，近年来，江西省规模以上工业增加值增速持续稳居全国第一方阵。

目前，正值我国重点调整产业结构、优化产业格局之际，江西省作为近年来经济增速始终位于第一梯队的省份，不乏有学者对江西省经济发展能力做出分析，主要集中在以下方面：分析城镇化水平和经济发展的关系(徐展峰 2012)，农村消费潜力对江西经济发展的影响分析(万国京 2014)以及人才资源对江西经济发展的影响分析(闵芸芝，周明 2013)。目前江西省工业面临着稳增长与提质量的双重挑战，要实现江西省工业高质量跨越式发展，必须牢牢把握工业强省战略，针对各个城市不同的情况，因地制宜发展最佳产业，构建现代化产业体系，本文具体研究了江西省11个城市的经济发展能力。

一、分析过程

(一)变量选择

城市经济发展能力指标体系的构建除了考虑地方的经济总量之外，还要考虑到经济质量和经济效能，因此本文提取了8个变量，分别是城市、人口、2019年前三季度GDP、人均GDP、财政总收入、社会消费品零售总额、城镇和农村人均可支配收入，8个变量分别定义为V1-V8，选取的11个观测样本分别是江西省的11个地级市。

(二)数据描述性分析

在搜集好数据、选择好变量和模型之后，接下来就是将数据录入Stata软件中进行处理，得到最后的实证结果。第一步，在将数据从Excel导入Stata后，在Stata14的Command文本框中输入命令：summarize V2-V8，就能考察所有变量的统计特征，也就是数据的描述性统计结果。

从统计结果中可以得出江西省11个城市的各项经济指标的平均数、标准差、最小值以及最大值，可以看出江西各市间的经济发展水平差距较大，尤其体现在GDP和社会消费品零售总额水平上，省内GDP最高的南昌市是最低的鹰潭市的6.5倍，社会消费品零售总额最高的南昌市是最低的鹰潭市的9.5倍。那么我们具体分析一下江西省各市的GDP情况，在Command文本框中继续输入命令：summarize V3,detail，得到以下具体的GDP描述性统计结果：

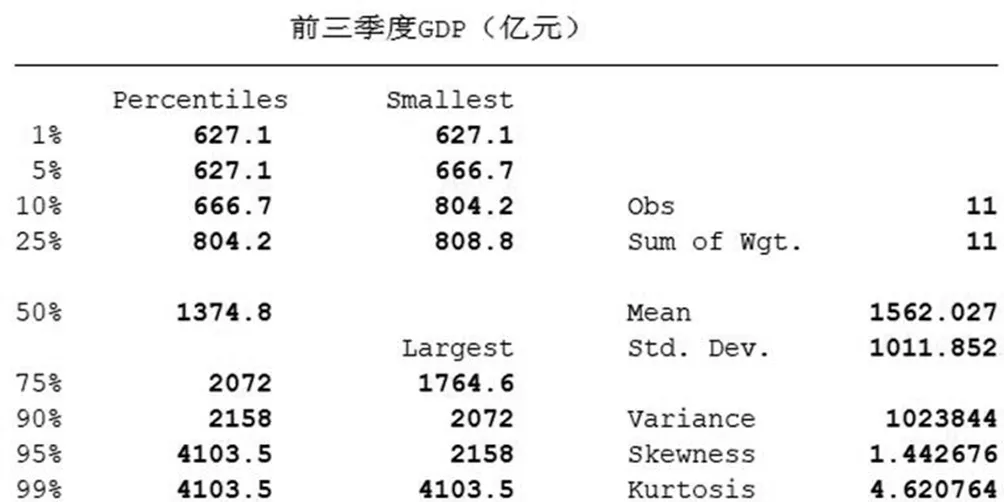
由图可以看出，GDP这一变量百分位数的第一个四分位数是804.2，第二个百分位数是1374.8；四个最小值分别为627.1、666.7、804.2、808.8；四个最大值分别为1764.6、2072、2158、103.5；均值为1562.027，标准差为1011.852，偏度为1.442676，为正偏态；峰度为4.620764，有一个比正态分布较短的尾巴。通过描述性分析可以看出，其它各个变量的所有数据都没有极端值和异常值，数据间的量纲差距也在可接受范围之内。

(三)数据相关性分析

接下来进行数据相关性分析，在Stata14的Command文本框中输入命令：pwcorr V2-V8,sidak sig star(0.01)，分析7个变量间相关性在置信水平为99%时是否显著。

由此分析可以得出GDP与财政总收入之间的相关系数为0.9869，与社会消费品零售总额之间的相关系数为0.9774，具有很强的相关性；财政总收入与社会消费品零售总额之间的相关系数为0.9484，具有很强的相关性；此外GDP与人口数的相关性较强，与人均GDP、城镇、农村人均可支配收入的相关性都较弱。

由上可以看出，江西省各市的经济发展水平并不是完全和人口成正相关的，总的来看省会南昌的各项经济数据都领先全省，但南昌人口只有554.6万，因此人均水平更是遥遥领先，赣州人口高达864万，GDP却只有南昌的一半，城镇、农村人均可支配收入也比南昌低很多，经济发展水平有待提高。

(四)数据回归分析

1.建立回归模型

考虑到GDP与人均GDP、城镇人均可支配收入和农村人均可支配收入变量间相关性较弱，本文把GDP作为因变量，把人口数、财政总收入和社会消费品零售总额作为自变量进行多重线性回归，在Command文本框中输入如下命令:sw regress V3 V2 V5 V6,pr(0.1)，得到如下结果：

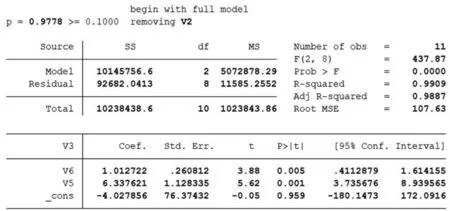
建立线性模型：V3=a*V2+b*V5+c*V6+u，即：GDP=a*人口数+b*财政总收入+c*社会消费品零售总额+u，式中a、b、c是未知的回归系数，u是随机误差项。

2.模型修正

模型经过一次剔除变量后得到最终结果，该模型V2变量的系数显著性P值高达0.9778，被剔除，之后得到最终回归模型。

从上述分析结果中看出模型的F值(2,8)=437.87，P值(Prob>F)=0.0000，说明该模型整体非常显著。模型可决系数(R-squared)是0.9959，模型修正可决系数(Adj R-squared)=0.9887，说明模型解释能力非常优秀。

在回归线性模型中变量V6的系数标准误是0.260812，t值为3.88，P值为0.005，系数比较显著，95%的置信区间为[0.4112879,1.614155]，同理可知V5的同类数据。常数项的系数标准误是76.37432，t值为-0.05，P值是0.959，系数是显著的，95%的置信区间为[-180.1473，172.0916]。

因此线性模型：V3=6.337621*V5+1.012722*V6-4.027856

即GDP=6.337621*财政总收入+1.012722*社会消费品零售总额-4.027856。

3.因变量拟合值的预测

因变量预测拟合值是根据自变量的值和得到的回归方程计算出来的，主要用来预测未来。在Command文本框中输入rvfplot后得到残差与拟合值的散点图。结果是残差并随着拟合值的大小的不同而不同，围绕0值上下随机波动，数据很可能是存在异方差。

4.异方差的检验

在Command文本框中输入estat imtest,white，得到怀特检验结果，可得P值=0.3497，拒绝原假设，不存在异方差。

(五)主成分因子分析

1.因子分析

在Command文本框中输入factor V2-V8,pcf，得出因子分析结果如下：

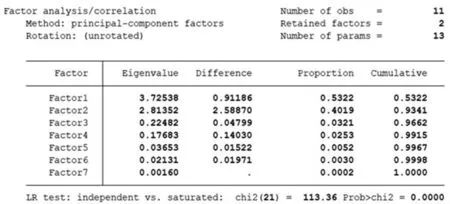
7个因子中只有2个因子特征值(Eigenvalue)大于1，选取这2个因子分别作为新的综合评价指标，LR检验的卡方值为113.36，P值(Prob>chi2)为0.0000，模型非常显著。第一个因子的特征值(Eigenvalue)为3.72538，方差贡献率(Proportion)为53.22%；第二个因子特征值为2.81352，方差贡献率为40.19%，前2个因子的累计方差贡献率(Cumulative)为93.41%，解释了原始数据的93.41%的信息。

2.因子结构旋转

采用最大方差正交旋转法对因子结构进行旋转，在Command文本框中输入rotate,再输入predict F1 F2，得出因子得分系数矩阵，由此写出主因子的表达式：

F1=0.23126*V2+0.27428*V3+0.01049*V4+0.27748*V5+26291*V6-0.07617*V7-0.03646*V8；F2=-0.24475*V2+0.01493*V3+0.31063*V4-0.01946*V5+0.05270*V6+0.27597*V7+0.32536*V8

3.KMO检验

在Command文本框中输入estat kmo进行KMO检验，判断数据是否适合进行因子分析，其取值范围是0～1，其中，0～0.5表示不可接受，0.5～1表示可以接受。检验得出总体(Overall)KMO的取值为0.5739，因子分析处于可以接受状态。

4.各城市综合得分

接下来依据提取的主因子对西藏各城市经济发展能力给出综合得分并进行排名。在Command中输入命令generate F=0.6147*F1+0.3307*F2可求出江西各城市经济发展能力的综合得分，其中F1、F2是在进行因子分析时候对提取的主因子保存的变量，系数是主因子的方差贡献率。可以得出各市综合得分：

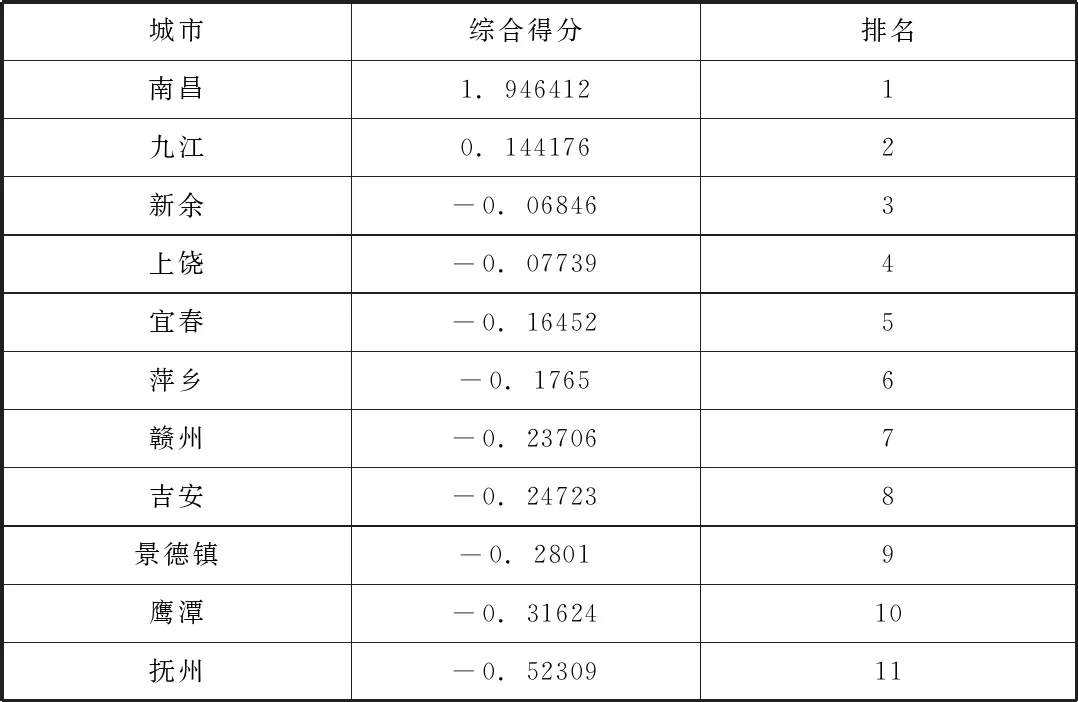
城市综合得分排名南昌1.9464121九江0.1441762新余-0.068463上饶-0.077394宜春-0.164525萍乡-0.17656赣州-0.237067吉安-0.247238景德镇-0.28019鹰潭-0.3162410抚州-0.5230911

二、结论与建议

经过主成分因子分析后，可以看出南昌作为江西的省会，各项经济指标明显领先全省，综合得分和两个主因子得分均是第一，属于省内的第一梯队城市。九江的综合得分仅次于南昌，但从各项指标和得分情况来看和南昌的差距较大，第三名新余和第四名上饶综合得分差距不大，都属于省内发展水平较好的城市。值得关注的是，赣州作为省内人口最多的城市，虽然目前经济发展水平不高，但从另一方面来讲，在人口红利逐渐消失的未来，人口资源将是一个城市发展最重要的资源，在这一点上赣州有着绝对的优势，未来务必要出台政策留住人才甚至吸引人才。

宜春、上饶、萍乡这个城市综合得分差距不大，这几个城市发展质量有待提高，经济总量和人均水平都属于较低的水平。萍乡、鹰潭和抚州由于人口较少，导致综合得分较低。这些城市的当务之急是优先发展第二产业，适当发展第三产业，总量提高了，人均水平自然也随之上涨

最后对提升江西省的整体综合经济发展能力提出以下建议：

1.首先要加强基础设施建设，完善交通网，为提高综合经济能力的发展提供保障。

2.坚持开放和创新的思想，重点解决发展不平衡、不协调、不可持续等突出问题，因地制宜发展特色产业，统筹兼顾，缩小贫富差距。

3.加强与国内其他城市的协同发展，积极整合省内、国内及国外的各种资源，资源共享从而发挥信息优势。

4.完善人才政策，经济发展离不开人才，南昌去年颁布的落户政策值得全省推广，江西要发展必须减少人才外流甚至吸引外省人才。