体声波磁电天线辐射性能的解析计算
彭春瑞,李君儒,钟 慧,任万春,高 杨
(1.电子科技大学 电子科学与工程学院,四川 成都 610054;2.重庆大学 光电工程学院,重庆 400044;3.西南科技大学 信息工程学院,四川 绵阳 621010)
0 引言
无线通信系统飞速发展,而天线作为无线电通信系统重要的前端器件,其在通信系统中的重要性与日俱增。天线不断向小型化、集成化及高性能化方向发展。传统的电小天线通过电流传导作用来辐射电磁波,当其辐射平面与接地平面距离过近时,由于在接地平面上产生了方向相反的镜像电流,削弱了天线辐射能力,从而导致天线辐射品质因数(Q)增大,阻抗匹配难,且其小型化也难以实现[1-2]。体声波磁电天线[3-4]利用磁电效应来辐射电磁波,其工作过程中不涉及电流的传导,从而在辐射机理上解决了因电流传导造成的辐射功率过低的问题,其辐射性能得到大幅提高。体声波磁电天线利用声波谐振原理可实现小型化,且在现有微机电系统(MEMS)制造工艺的基础上可实现量产,应用市场前景广阔。
然而,该天线的理论设计与评估方法还存在很多空白。目前更多是用时域有限差分法评估磁电天线,该方法对时间步长和空间步长有着严格的要求,不同器件的步长不同,求解过程相对复杂,且相对于解析法,数值计算误差较大[5-7]。因此,建立一套准确的天线性能分析模型尤为重要。YAO等[8]提出了一种天线辐射Q值的简化模型,但该模型做了很多近似相等的假设,导致计算结果严重失真。
本文在此模型基础上提出了一种新的体声波磁电天线辐射性能的解析计算方法,并利用该方法研究了交替多层结构天线的层数对其辐射性能的影响。
1 体声波磁电天线的工作原理
磁电(ME)效应[9](见图1)是材料在外磁场H作用下产生介电极化(正ME效应),或在外电场E作用下产生磁极化(逆ME效应)的特性,ΔM为磁极化增量。
磁电天线利用逆磁电效应来发射电磁波。图2为双层磁电天线工作原理。由图可知,在压电相两端加激励电压时,由于压电效应,压电材料会产生动态应变,而动态应变在压电相和压磁相的界面处连续传递,使压磁相产生动态磁通B,同时产生时变的孔径电场E0和H,进而向外部辐射电磁波。

图2 双层磁电天线工作原理
实际应用中,按照磁电天线的工作原理,可将其设计为不同功能层(压电层/磁致伸缩层)交替堆叠的磁电天线结构,如三层结构(压电层-磁致伸缩层-压电层)磁电天线、四层结构(压电层-磁致伸缩层-压电层-磁致伸缩层)磁电天线,以此类推。交替层数不同,天线的辐射性能也不同,需要从理论上找出最优解。
2 势能
从电磁场应变的本构方程[10]出发,推导出磁电天线势能的计算公式。
压电应变本构方程为
(1)
压磁应变本构方程为
(2)
式中:TE,TH为应力张量,下标E、H分别为在恒定电/磁场条件下测得;SE,SH为应变张量;E,H为电/磁场强度矢量;D,B为电/磁通密度矢量;μT,εT为无应力磁导率和介电常数;sE,sH为力学柔度常数;dE,dH为应变常数。
将式(1)、(2)改写为一维形式:
压电相:
(3)
(4)
压磁相:
(5)
(6)
式中:sB,sD为力学柔度常数,下标D,B分别为恒定电/磁通密度条件下测得;S,T分别为一维形式下的应变、应力张量;E,H分别为一维形式下的电/磁场强度矢量;D,B分别为一维形式下的电/磁通密度矢量。
显然,压电相与压磁相两种材料之间的应变场连续,应力场并不连续,但两种材料之间应力场分别服从正弦分布。假设压电相中的应力场为T1,压磁相中的应力场为T2。
分别对磁电天线的压电相和压磁相的势能进行计算。压电相的总势能是以机械应力形式的机械能和电场形式的电能储存的。压磁相的总势能是以机械应力形式的机械能和磁通量密度形式的磁能储存的。
因此,对于压电相的势能有:
(7)
压磁相的势能有:
(8)
为了方便计算,对于压电相取开路激励条件D=0,并代入式(3)、(4)可得
(9)
S=sDT1
(10)
式(7)可化简为
(11)
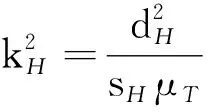
(12)
磁电天线的总势能为
WP=WPM+WPE=
(13)
将给定的应力场分布条件代入式(13),可分别计算出2~6层体声波磁电天线的总势能表达式,其结果如表1所示,表中,h为压电/压磁相厚度,A为压电/压磁相截面面积。

表1 2~6层磁电天线势能总和
以AlN和FeGaB为例[1],FeGaB的柔度系数约为AlN的4倍,即sH=4sD。由胡克定理可知,应变为应力与柔度系数的乘积,n=4。其归一化的势能结果如图3所示。磁电天线的总势能与其层数成正相关,且在2、3层结构之间的增幅最大。

图3 2~6层磁电天线归一化总势能
3 平均辐射功率
多层磁电天线的辐射过程是由外加在压电相的电流源激励起压电材料内部的垂直动态应变[11]。这种动态应变激励压磁相产生动态磁通,从而在压磁相的表面产生孔径电场。
天线的平均辐射功率为
(14)
法拉第电磁感应定律的一维形式:
|E|=ωh|B|
(15)
式中ω为角频率。
在弱磁场条件下,结合式(5)、(6)、(14)和(15)推导出在给定应力情况下的磁电天线的平均辐射功率为
(16)
将式(16)在压磁相的厚度范围内取均值可得
(17)
式中h1,h2为压磁相的厚度。
利用式(17)可分别计算出2~6层体声波磁电天线的平均辐射功率,其结果如表2所示。

表2 2~6层磁电天线平均功率
续表

层数平均功率表达式63T20ω2h2d2HA4η0


图4 2~6层磁电天线归一化辐射功率
4 归一化辐射品质因数
磁电天线的Q决定了其辐射性能的好坏,Q值越低,则辐射性能越好。
磁电天线的Q定义为
(18)


图5 2~6层磁电天线归一化辐射品质因数
5 结束语
该解析计算法解决了以往YAO等将压电层柔度系数与磁致伸缩层的柔度系数近似等价的计算问题,克服了只能计算2层结构磁电天线辐射性能参数的局限性。本文创新性地提出了利用正弦应力场分布计算交替多层结构磁电天线平均辐射功率的解析计算方法,从而计算出归一化辐射品质因数。
另外,通过上述解析计算结果可知,“压电层-磁致伸缩层-压电层”3层结构的磁电天线的平均辐射功率相对增幅最大,且品质因数为最小值,辐射性能最好。因此,3层堆叠结构的磁电天线是设计中的最优选,该研究成果对后续器件设计、仿真和制备具有重要指导意义。

