基于两阶段随机森林的螺丝锁附结果判别研究

邓 煜，李 明，周稻祥

(太原理工大学 大数据学院，太原 030024)

当代社会，手机由只能打电话发短信逐渐发展成为移动数字媒体终端，是人们日常生活的重要组成部分。因此，手机需求量急剧上升，仅2018年全国手机销量已过亿部。销量的激增对手机装配提出了更高的要求。目前，我国手机装配依然以人工装配为主，在手机装配生产线上，很大一部分操作就是螺丝锁附，工人依靠掌上型螺丝机进行螺丝锁附操作。人工操作在面对如此庞大的手机需求量时，问题频出，主要问题有以下几点：1) 工人技术水平参差不齐；2) 工作强度高导致的合格率下降；3) 工厂人力成本较大。因此，工业化、机械化生产是企业提高效率、降低成本的最佳选择，智能螺丝机开始在生产线中替代人工操作。

智能螺丝机在作业过程中，有一个步骤是对螺丝锁附结果进行判断，以帮助螺丝机进行后续操作。因此，判断螺丝锁附结果就成为智能螺丝机的核心要点。目前，大多数智能螺丝机都是根据生产经验对电批参数划分范围，将参数范围与螺丝类别进行对应。但由于相似类别的参数范围重叠部分较多，故容易导致智能螺丝机发生误判，整体判别准确率较低。本文首先尝试通过机器学习算法建立分类模型来对螺丝锁附结果进行判别，但螺丝锁附数据有着数量大、类别多、维度高且每条数据长度不定等特点，无法直接使用分类算法进行分析。针对这些问题，本文从锁附数据的物理特性(角度、扭矩、速度)出发，对锁附数据序列进行特征重构(如最大角度、最大扭矩等)；然后使用分类算法，如支持向量机[1-2]、随机森林[3-5]、K-近邻算法[6]、逻辑斯特回归[7]等进行分类。实验结果虽然比传统智能螺丝机使用的置信区间法准确率高，但仍未达到工业级别大规模生产所要求的准确率。

引起分类结果不理想的原因主要有以下几点：1) 经重构得到的特征优劣不一。由于是对原始数据进行特征重构，无法保证重构特征的有效性，有些无用的特征数据甚至会扰乱分类结果。因此需要对重构的特征进行筛选。2) 相似类别之间的误判问题依然没有得到有效的解决，仅凭借重构特征还不足以解决误判问题，需要新的特征和新的方法来提高判别准确率。

针对上述问题，本文提出了基于两阶段随机森林的螺丝锁附结果判别模型，在第一阶段中通过特征构造和基于随机森林的特征筛选方法处理数据；第二阶段将各物理特性的概率主成分分析方差作为特征进行聚类，以聚类生成的预分类簇区分相似类别与非相似类别数据，对各簇分别使用随机森林建立分类模型，汇总构成螺丝锁附结果判别模型。

1 预备理论

1.1 随机森林

随机森林[8]是Bagging的一个扩展变体，随机森林在以决策树为基的学习器上构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。对于基决策树的每个节点，先从该节点的属性集合中随机选择一个包含k个属性的子集，然后进行划分，其中参数k控制随机性的引入程度。正是由于随机性的引入，使得随机森林具有良好的性能，解决了决策树泛化能力弱的特点，且容易实现，计算开销小，准确率高，被誉为“代表集成学习技术水平的方法”。

基于决策树的构造原理，决策树中每个节点都是依据其特征重要度进行生成的，所以也能把决策树的构建看作为是一个特征选择的过程[9]。由BREIMAN[3]提出的基于随机森林的特征选择算法，通过在随机森林中加入高斯噪声，使得随机森林算法在兼备集成学习优点的同时具有更广泛的应用。若特征重要度高，则整体分类准确率下降明显；若特征不重要，则整体分类准确率无明显变化。

1.2 概率主成分分析

概率主成分分析(简称概率PCA)[10-12]是从概率的角度来对PCA进行分析的。

引入隐变量z及其分布P(z)，观察变量x是由z产生的，因此有条件分布P(x|z)，假设z服从0均值单位方差的高斯分布，则有：

z～N(0,I) .

(1)

x～N(μ,WWT+ψ) .

(2)

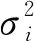
x～N(μ,WWT+σ2I) .

(3)

x=Wz+μ+σm.

(4)

(5)

2 智能螺丝机锁附结果判别模型

目前，智能螺丝机使用的置信区间法，是通过对角度、速度、扭矩3个物理特性划分置信区间来判断锁附类别。置信区间法在处理相似类别数据时经常发生误判，针对该问题，本文提出了基于两阶段随机森林的智能螺丝机锁附结果判别模型。

假设原始训练数据集为D，重构特征个数为n，最优特征个数为m，平衡数据集个数为p，生成的预分类簇个数为q.算法流程如图1所示。

图1 基于两阶段随机森林的螺丝锁附结果判别模型Fig.1 Discrimination model of screw locking results based on two-stage random forest

算法基本分为以下几个步骤：

1) 第一阶段。

a.对螺丝原始数据进行特征重构；

b.对数据集D进行欠采样，生成平衡数据集；

ReSamplingD={ReSamplingD1,ReSamplingD2,…,ReSamplingDp}

c.结合ReSamplingD使用随机森林进行特征筛选，得到一个最优特征子序列R=[r1,r2,…,rm].

2) 第二阶段。

a.对R中的特征按照所属物理特性重新进行排列，得到3个特征序列RA，RS，RT；

c.在各簇上分别建立分类模型，将分类模型汇总，得到螺丝锁附结果判别模型。

测试数据通过模型进行判别时，先计算与各预分类簇质心的欧式距离，确定所属簇，再通过簇内分类器确定锁附类别。

2.1 模型第一阶段

图2列出了螺丝锁附时常见类别的扭矩序列图，包括锁附OK，锁歪，浮高，滑牙，未锁入，空转等6种类别。针对螺丝锁附过程中产生的数据特性，本文对其物理特性进行如下的特征构造：1) 数据中的最大值，50%分位数；2) 均值，一阶差分绝对值的和以及方差；3) 不同锁附阶段中的特征构造1)，2).这些特征能够有效地刻画螺丝锁附过程中物理特性的波动变化，所以使用这些特征来代替原始数据。

本文对螺丝锁附数据采取随机森林变量选择方法进行特征筛选[13]，并使用后向搜索方法，将每次特征重要度最小的特征剔除，同时计算每次剔除后的模型分类准确率，将准确率最高的特征序列作为最优特征子序列。

由于实际生产中产生的各类锁附数据的数据量不同，导致数据不平衡[14-15]。传统机器学习算法在不平衡数据上具有偏向性，更倾向于数据量大的类别。因此本文基于Bagging算法的采样思想，尝试一种欠采样式[16-18]的平衡采样法，其基本思路如下：

图2 常见锁附类别扭矩序列图Fig.2 Common attached torque sequence diagram

1) 将多数类独立随机抽取若干子集，且子集数量和其他少数类数目基本相同。

2) 将少数类进行Bootstrap取样，得到和步骤1)中相同个数的子集。

3) 将各类子集重组最终得到平衡数据集

ReSamplingD={ReSamplingD1,ReSamplingD2,…,ReSamplingDp}.

通过平衡采样法多次构造得到不同的欠采样数据集可以反映不同的欠采样结果，这比单一欠采样得到的数据集包含更多的信息，本文尝试对训练数据进行多次欠采样，通过特征在ReSamplingD中各欠采样数据集中的综合表现来确定其特征重要度。

在得到平衡数据集后，开始计算特征的特征重要度。本文对特征添加高斯噪声，将添加前与添加后分类准确率变化值作为该特征的重要度(若某特征重要，添加噪声后，模型分类准确率将大幅下降，反之，模型分类准确率无明显变化)。记添加噪声前模型的分类准确率为Apre，添加噪声后的分类准确率为Ac，其中c代表第c个特征。在传统随机森林中，经常使用Out-of-Bag数据集(即OOB数据集)来测试随机森林的效果，但由于OOB数据集是随机产生的，会导致测试数据内部类别不平衡，无法有效度量模型效果，所以本文采用最常见的3-折交叉验证法对每一个生成的平衡数据集都进行交叉验证，则第c个特征的特征重要度(Feature Important,FIM)为：

(6)

式中：i代表第i个平衡数据集；k代表每个数据集第k次交叉验证；p代表ReSamplingD中数据集的个数。

在每次进行特征重要度排序后，剔除特征重要度最小的特征，并计算该次迭代的模型分类准确率，最终完成迭代后，将分类准确率最高时的特征子集作为最优特征子集。

2.2 模型第二阶段

传统判别方法中的误判现象，主要是由于相似类别之间分类效果较差造成的。因此，需要对相似类别单独建立分类模型，提高分类准确率。本文首先对各物理特性使用概率PCA方差进行描述，根据方差值使用K-Means算法进行聚类，得到若干预分类簇。每一个簇内都是类别相似性较高的数据，而簇与簇之间类别相似性较低。对各簇分别使用随机森林算法建立分类模型，增强分类器的分类性能。

实验初期进行聚类时，尝试过多种描述属性关系的方法(如距离相关系数，皮尔森相关系数等)，但聚类效果普遍较差，无法有效地将相似类别与非相似类别进行区分。经反复尝试，对螺丝数据提出了一种基于概率PCA方差的聚类方式。概率PCA是传统PCA概率化的方式，相对于传统PCA优点在于引入了方差σ2[19-20]。概率PCA曾被应用在图像处理的缺陷检测[21]中，通过对比样本图像与标准图像的σ2大小来判断是否为缺陷点。本文受此启发，将概率PCA中的σ2作为一种描述状态的特征，对螺丝锁附数据中的每个物理特性根据对应的重构特征(如角度中的最大角度，角度50%分位数等)都求得一个σ2作为特征值，然后使用K-Means算法对这些特征值进行聚类。

在使用K-Means算法进行聚类时，聚类效果通常是根据轮廓系数来决定的，但由轮廓系数确定的聚类结果在各簇之间存在类别混淆问题，本文希望簇与簇之间的类别尽量不重叠，故提出了一个类别错分率作为聚类效果的标准。记某类别共有s个样本，某簇含有该类别的样本最多，样本个数为t，那么认为其他簇中的该类别数据都是错误聚类的结果，则该类别数据的错误聚类样本数为s-t.将所有错误聚类样本数求和除以整体样本数得到类别错分率(Category Error,CE)，即：

(7)

式中：j为第j个类别；d为类别个数；l为总体样本个数。类别错分率越小，说明各簇中数据类别更集中，簇与簇之间的数据类别界限更清晰，当类别错分率为0时，说明簇与簇之间的数据没有发生类别混淆的情况。

3 实验结果与分析

本节首先对两阶段分别进行实验，验证其有效性，然后对本文的锁附结果判别模型进行实验分析，并与传统置信区间法及多种机器学习分类算法进行对比、评估。

3.1 模型评估标准

本文根据如表1所示的混淆矩阵，得到各类别的评价指标，即精确度、准确率、召回率和F值。精确度表示预测模型将所有样本正确预测的概率。召回率反应了预测模型对某一类的预测性能，值越大，代表这一类中越多的样本被预测正确。准确率是指预测为某类样本的正确数量占所有预测为该类样本数量的比例。F值是召回率和准确率的调和值，两者相互作用，一个量增加会引起另一个量减少。

在螺丝锁附数据中，各类别样本数相差过大，实际生产中对样本量小的类别，如锁歪、未锁入的情况更加重视。多分类问题中宏平均的计算方式对样本量少的类别更加敏感，本文利用宏平均的思想，在各类混淆矩阵上分别计算出准确率、召回率和F值，再求平均值，得到总体模型的准确率、召回率、F值。

表1 混淆矩阵Table 1 Confusion matrix

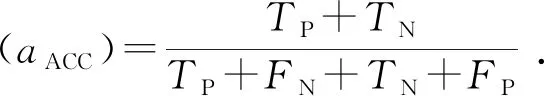
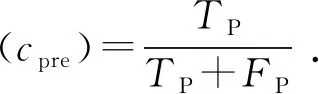
3.2 第一阶段实验

3.2.1数据处理

本文数据采集自实验室智能螺丝机，选用同一电批在相同参数下2018年3月到2018年7月采集的数据作为训练数据。用到的螺丝数据共4 612颗，其中锁附结果为OK的螺丝数为3 068颗，锁歪527颗，浮高286颗，滑牙208颗，未锁入336颗，空转187颗。每颗螺丝产生的数据是一个L×5的矩阵，L表示序列的长度，矩阵的第1列为序号，第2列为时间长度，每0.001 s记录一组数据，第3列为不同时间点的转角值，第4列为锁附螺丝过程中所用的扭矩值，第5列为螺丝旋转速度。电批在对螺丝进行锁附时，基本能分为两个阶段：第一阶段是电批吸附螺丝在螺孔上方认帽，此时螺丝会空转一段时间；第二阶段是电批下压，螺丝锁入螺孔。

如表2所示，本文针对螺丝锁附过程的3个物理特性：角度、速度、扭矩，提出了一些对分类有用的特征。

经过数据重构后，样本数据可用一个4 612×(15+1)的矩阵表示，其中，4 612为样本总数，15是特征个数，最后一列为分类标签，即螺丝锁附结果。

测试数据选用2018年7月-9月采集的数据进行验证。

表2 特征重构后的特征列表Table 2 Feature list after feature reconstruction

3.2.2特征筛选

使用节2.1中的欠采样法对训练集进行采样，共得到10个数据集。通过式(6)计算特征重要度并进行特征筛选，得到最优特征子序列如下：

{1,2,4,5,8,9,10,12,13}.

图3给出了每次迭代时模型的精确度，可以看出特征数为9时模型精确度最高，达到81.9%，高于未筛选时的72.6%.因此证明了特征筛选的有效性。

图3 特征个数与模型预测精确度Fig.3 Number of features and model prediction accuracy

3.3 第二阶段实验

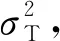
对于预分类簇的确定，本文曾尝试使用多种描述变量关系的特征进行聚类，如皮尔逊相关系数，距离相关系数，最大信息系数，但效果不佳，在不同簇上经常有类别混淆，对3.2.1中的数据进行实验，结果如表3所示。

表3 不同算法下的聚类效果Table 3 Clustering effects under different algorithms

由表3可知，类别错分率越小，各簇中数据类别越清晰，整体模型的判别精度也越高。在基于概率PCA方差进行聚类时，类别错分率最小，仅3.6%，此时判别模型精确度最高为93.8%，高于未进行预分类的81.9%，证明概率PCA方差对螺丝数据描述效果更好，能够帮助完成相似类别的聚类任务，从而提高整体模型判别精确度。

3.4 螺丝锁附结果判别模型实验

利用3.2.1中的训练集与验证集进行实验，判别结果如表4所示。由表可以看出，数据在预分类簇的基础上由各簇内部分类器进一步分类的螺丝锁附结果判别模型，在各类别上区分度较高，召回率和准确率均能保证在85%以上。整体精确度为93.8%，对螺丝数据有较好的判别效果。

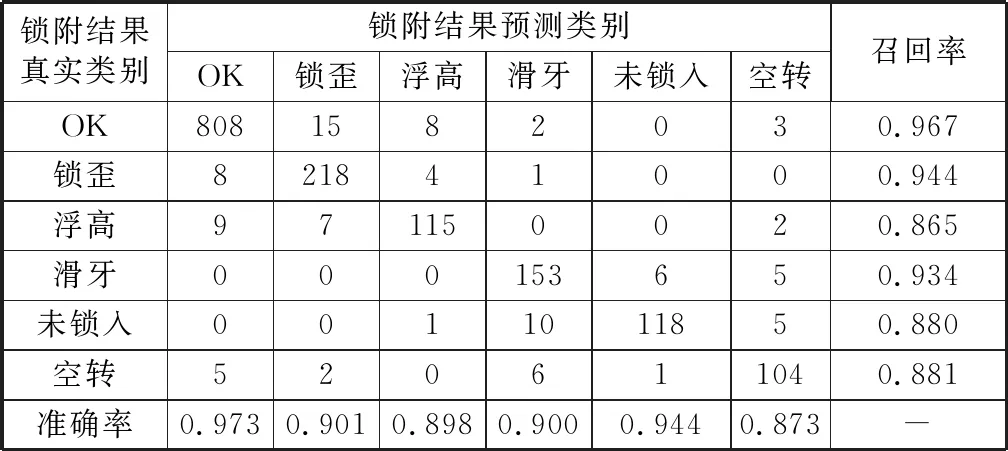
表4 螺丝锁附结果判别混淆矩阵Table 4 Confusion matrix of screw locking discrimination results

为检验本文算法各模块的有效性，对①特征重构；②未加入平衡数据集的特征筛选；③基于平衡数据集的特征筛选；④预分类簇进行验证，验证结果如表5所示。由表可得，各模块在对螺丝锁附结果判别上有明显的提升效果。

表5 不同模块下模型评估参数Table 5 Model evaluation parameters under different modules

为验证算法对螺丝锁附数据的普遍适用性，取同一电批不同月份采集的数据进行分析，结果如图4.由图4可得分类精确度均高于0.85，相较传统置信区间法精确度有很大提升，且普遍适用。

本文使用多组数据进行验证，将传统置信区间法，多种机器学习分类算法(数据仅进行特征重构)和本文模型的结果进行对比，取各组数据的平均结果，如表6.

由表6可得，本文提出的模型在准确率、召回率和F值上均高于其他方法，对螺丝数据有更好的判别效果。

图4 不同批次数据验证结果Fig.4 Different batch data verification results

表6 不同算法效果对比Table 6 Comparison of different algorithm effects

4 结束语

本文针对螺丝锁附结果判别中遇到的问题，提出了一种基于两阶段随机森林的螺丝锁附结果判别模型，第一阶段对原始数据进行特征重构，特征筛选，第二阶段对锁附数据使用基于概率PCA方差的K-Means算法进行相似类别聚类，并分别使用随机森林建立分类模型，加强分类器对相似类别的分类效果，最终汇总构成螺丝锁附结果判别模型。该模型在精确度、召回率等方面都优于目前智能螺丝机的置信区间法及多种机器学习分类方法，可以提高智能螺丝机的识别精度，降低生产成本。

在该模型的基础上，今后还可在锁附过程中进行动态预测，根据锁附曲线拟合程度对锁附结果进行预警，更高效地配合智能螺丝机完成螺丝锁附结果判断。