基于机器视觉的隧道衬砌裂缝图像分割处理算法研究

石 帅 王 睿 文思思 汤盈盈

(四川师范大学， 成都 610068)

隧道病害问题特别是隧道衬砌裂损问题严重威胁高速铁路的运营安全。受设计、施工以及复杂的使用环境等因素影响，隧道衬砌的混凝土结构会发生病害并影响其使用性及耐久性[1]。裂缝是混凝土结构常见的病害之一，当裂缝扩展到一定程度时，将导致混凝土受力状态发生改变，使结构破坏机率增大，同时还可能引发渗漏水、结构冻害等表观病害[2-3]。裂缝的开展状况是诊断、分析、评判已有隧道衬砌病态的重要依据之一。高速铁路隧道是一种在狭小空间内进行快速运载的复杂系统，空间的有限性决定了相应管理措施的难度和复杂性。受高速铁路运行密度及检修时间的限制，传统的隧道衬砌裂缝检测方法(人工肉眼检测或人工仪器检测)基本不可能完成检测任务。近年来，基于机器视觉检测的裂缝检测方法得到广泛应用，该方法的关键在于能从采集图像中准确提取病害信息，即对图像中的背景和裂缝进行分割提取，进而实现高效率、低影响的裂缝检测。图像分割越准确，对后续裂缝信息的提取越有保证。

图像分割(阈值分割)技术是指将图像中目标区域和背景区域分割开来的图像二值化技术[4]。至今已有多种阈值分割方法[5-7]。本文应用Otsu法、迭代法、最小误差法、最大熵阈值分割法4种常用方法对采集的裂缝图像进行分割，对各种算法处理效果的优劣进行系统分析。

1 图像阈值分割传统算法

1.1 Otsu法

Otsu法[8-10](最大类间方差法)运用聚类的思想，借助大津法求得的阈值进行图像二值化分割，即按灰度值把图像所有像素点分成两部分，使得两部分之间的灰度值差异最大，每个部分内部的灰度差异最小。方差是图像灰度分布均匀性的一种度量，背景和裂缝之间的类间方差越大，说明构成图像的两部分的差别越大；部分裂缝错分为背景或部分背景错分为裂缝都会导致两部分差别变小，使类间方差最大意味着错分的概率最小。该算法的运算步骤如下[11]：

(1) 设图像中有L个灰度等级，则图像中总的像素N和每个灰度值的概率pj,可由式(1)求得。

(1)

式中：nj——灰度值为j的数目。

(2) 任意在(0-L)灰度内选取一个灰度值T，将图像分成背景和裂缝两部分。令背景为 A部分，裂缝为B部分，则A和B两部分的灰度平均值GA、GB，可由式(2)求得。

(2)

(3) A部分占总像素的比例PA和B部分占总像素数的比例PB,可由式(3)求得。

(3)

图像总体灰度均值G=GAPA+GBPB。

(4)类间方差可由式(4)求得。

σ2=PA×(GA-G)2+PB×(GB-G)2

(4)

由此可知，最佳阈值T就是使σ2最大的灰度值。

1.2 迭代法

迭代法是一种通过迭代求出图像分割阈值，将图像与背景分开来的算法。迭代法求阈值时，先预设置一个阈值T，对图像中灰度值大于T的像素点求出灰度平均值TA，对图像中灰度值小于T的像素点求出灰度平均值TB，若|TA-TB|<Δ，则当前T即为最佳阈值，否则取T=(TA+TB)/2，重复上述操作。该算法的运算步骤如下[12]：

(1)整幅图像的平均灰度值，可由式(5)求得。

Tave=∑P/N

(5)

式中：Tave——平均灰度值；

∑P——图像中所有像素的灰度总和；

N——总像素数。

将Tave设置为初始阈值Tk,此时k=1。

(2)将图像分割成背景和目标两个部分，将灰度值大于TA的称为背景部分，将灰度值小于TA的称为目标部分。再求出两个区域的平均灰度值，分别为Tlow和Thigh。

(3)根据上述操作，求出新的阈值Tk+1=(Thigh+Tlow)/2，若Tk+1≠Tk，则用Tk+1代替Tk，返回第二步重新进行循环，并对k进行赋值，使k=k+1。循环直至Tk+1=Tk。

(4)将Tk+1作为最终阈值，进行二值化图像分割。

1.3 最小误差法

最小误差阈值法[13]假设图像裂缝和背景的灰度分布服从混合正态分布，通过函数选取最佳阈值，对图像进行二值化处理[14]。对于一幅大小为M×N的数字图像，用f(x,y)表示图像上坐标为(x,y)的像素点的灰度值，f(x,y)∈G=[0,1,…,L-1]。图像的一维直方图h(g)表示图像中各个灰度值出现的频数，故用一维直方图作为图像概率分布的描述。假设理想的灰度分布模型是混合正态分布：

(6)

式中：p(i)——子分布的先验概率；

p(g|i)——p(g)的二个子分布，分别服从均值为μi，方差为σi的正态分布。

任取一阈值T把图像分割成A、B两部分,该算法的运算步骤如下：

(1) 计算出图像两部分的灰度平均值PA、PB。

(7)

(2) 再计算图像两部分的灰度值期望μ和方差σ。

(8)

(3) 利用最小误差思想得到函数式(9),最佳阈值T即为使J(T)取最小值的T。

J(T)=1+2[PA(T)lnσA(T)+PB(T)lnσB(T)]-2[PA(T)lnP0(T)+PB(T)lnPB(T)]

(9)

(4) 通过对最佳阈值与灰度值进行比较，将图像二值化，得到最佳阈值像元归类方式为:

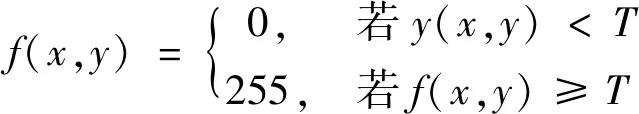
(10)

1.4 最大熵阈值分割法

熵是用来衡量一个分布的均匀程度，熵越大，说明分布越均匀。计算所有分割阈值下的图像总熵，找到最大的熵，将最大熵对应的分割阈值作为最终的阈值，图像中灰度大于此阈值的像素作为裂缝，小于此阈值的像素作为背景。最大熵阈值分割算法[15]的运算步骤如下：

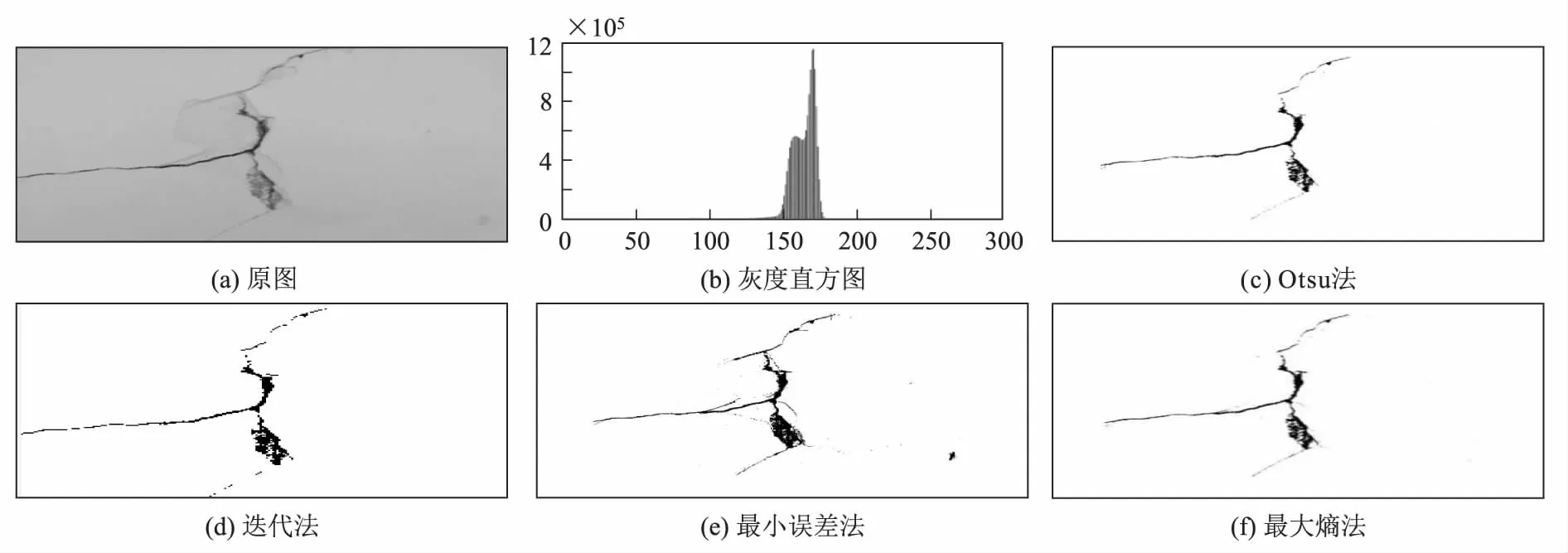
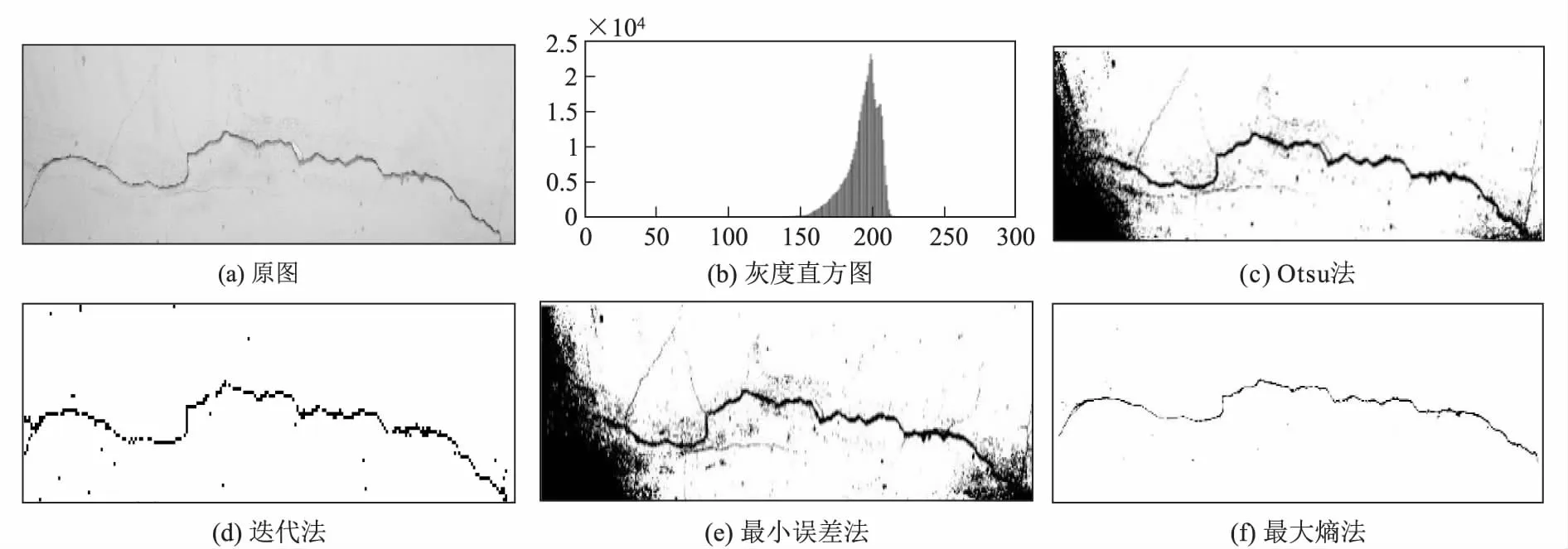
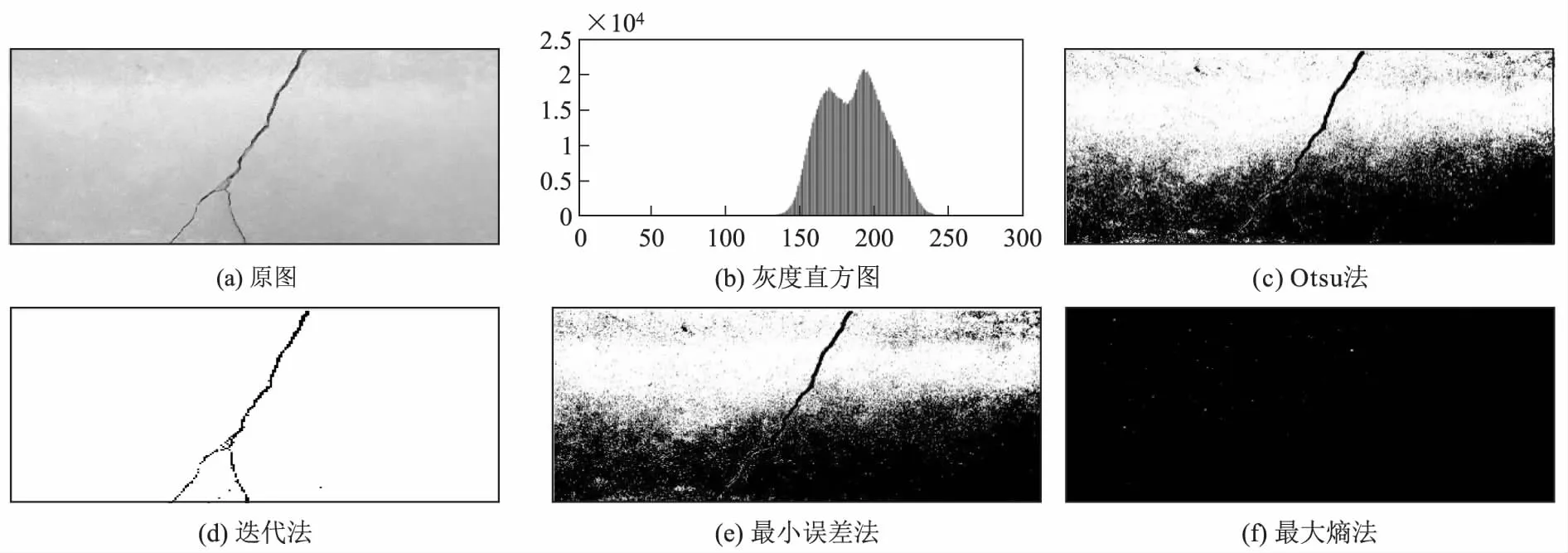
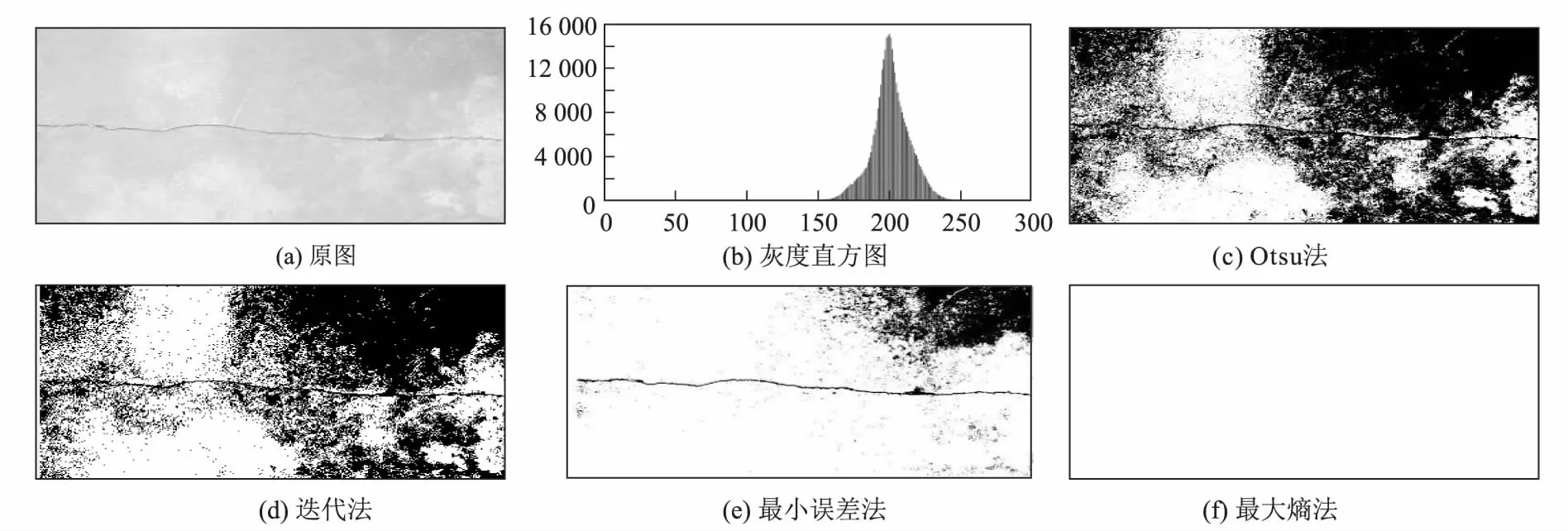
(1) 给定一个特定的阈值T(0<=T

(11)

(2)T阈值分割背景和目标像素的累计概率分别为PA(T)、PB(T)T，两者之和为1。

(12)

背景和目标的熵：

(13)

在该阈值下，图像总熵：

H(T)=HA(T)+HB(T)

(14)

(3) 计算所有分割阈值下的图像总熵，找到最大的熵，将最大熵对应的分割阈值作为最终的阈值，图像中灰度大于此阈值的像素作为裂缝，小于此阈值的像素作为背景。

2 图像处理结果分析

本文借助MATLAB软件对收集的隧道衬砌混凝土表面裂缝图像进行了模拟处理，直观得到4算法(Otsu法、迭代法、最小误差法、最大熵阈值分割法)的处理图像，并选取其中具有代表性的5组样本对处理结果进行对比分析。

(1)样本1的图像处理

样本1为有白色抹面的混凝土墙体，裂缝主体与背景灰度值相差较大，周边伴有少量与背景灰度值相近的剥落及细小裂缝，为较为理想的待处理样品，其样本原图及4种算法对裂缝图像的处理结果如图1所示。从图1中可以看出，4种算法的处理结果均能较好地保留裂缝主体，但Otsu法、迭代法和最大熵阈值分割法的处理图像中存在裂缝断裂、不连续，较浅剥落与背景混杂不清的情况，处理结果与裂缝原图像符合度一般；而最小误差法能捕捉到与背景颜色相近部分的细微裂缝，基本能真实反映裂缝的轮廓细节。

图1 样本1阈值分割结果图

(2)样本2的图像处理

样本2的裂缝主体连续，周边伴有较多的细小裂缝，且背景较样本1相对复杂，对算法处理精度的要求相对较高。其样本原图及4种算法对裂缝图像的处理结果如图2所示。从图2中可以看出，迭代法、最大熵阈值分割法的处理结果虽能基本反映裂缝的主体形态，但有断点、不连续现象出现，无法反映裂缝主体周边的细小裂缝；Otsu法、最小误差法处能较好地反映裂缝主体及周边的细小裂缝，但在图像的边角处，处理结果失真较严重，处理过程中将部分的背景区域划为了裂缝区域，影响了后续裂缝信息的提取。

图2 样本2阈值分割结果图

图3 样本3阈值分割结果图

(3)样本3的图像处理

样本3的裂缝主体清晰，但裂缝深度不一，且背景颜色不均，图像处理难度相对较高。其样本原图及4种算法对裂缝图像的处理结果如图3所示。从图3中可以看出，最大熵阈值分割法的处理图像严重失真，图像处理过程中，将背景区域全部划为目标部分，完全无法识别裂缝；Otsu法、最小误差法的处理图像部分失真，处理过程中将裂缝较窄、背景灰度值较低的背景区域直接处理成了目标部分，影响了对裂缝形态的识别；相较于其他3种方法，迭代法的处理结果较为完整地反映了裂缝的形态，但仍存在断点、不连续现象。

(4)样本4的图像处理

相较于样品1～3，样本4的背景灰度值整体较浅，裂缝较杂乱且裂缝周边伴有渗水现象。其样本原图及4种算法对裂缝图像的处理结果如图4所示。从图4中可以看出，最大熵阈值分割法对样本4表现出很强的不适用性，处理过程中将裂缝和渗水部分划为背景，处理图像严重失真；Otsu法和迭代法将裂缝、渗水部分以及部分灰度值较小的区域一同划为目标部分，无法识别裂缝形态，处理图像也严重失真；最小误差法的处理结果较为理想，不受渗水影响，能基本反应裂缝的形态，这是因为样本4的灰度直方图接近于正态分布，而最小误差法的算法原理就是运用正态分布函数进行阈值分割处理的。

(5)样本5的图像处理

样本5的裂缝形状较为规整，无细小裂缝，但背景较为复杂，噪点多，存在不均匀灰度分布。其样本原图及4种算法对裂缝图像的处理结果如图5所示。从图5中可以看出，最大熵阈值分割法对样本5同样表现出很强的不适用性，处理过程中，将裂缝全部划为背景；Otsu法和迭代法受背景干扰严重，处理时将裂缝和部分背景一同划为目标部分，导致处理结果无法很好地识别裂缝形态；样本5的灰度直方图也接近于正态分布，因此，最小误差法对样本5的处理效果也较理想，虽然边缘部分受到噪声干扰，但处理图像能较为清晰地反映裂缝形态。

图5 样本5阈值分割结果图

3 结论及建议

本文借助MATLAB软件对采集的隧道衬砌裂缝图像进行模拟处理，并通过对4种算法(即Otsu法、迭代法、最小误差法、最大熵阈值分割法)图像处理结果的对比分析，得到4种传统算法的优缺点，得出以下结论。

(1)Otsu法、迭代法、最小误差法、最大熵阈值分割法均能较好地处理裂缝与背景分离明显的理想图像。

(2)Otsu法能较好地处理与背景颜色相近的细微裂缝；迭代法在处理背景颜色分布不均的图像时，具有较明显优势；最小误差法在处理与背景颜色相近的细微裂缝和灰度直方图接近正态分布概率密度曲线的图像时，具有较明显占优势；最大熵阈值分割法易受背景噪点的干扰，总体处理结果不佳。

(3)下一步研究中，应结合图像分割中存在的问题，对传统算法予以改进。