基于CWT及STFT变换的两类地震动频谱特性分析
(1.西安工业大学 建筑工程学院 陕西 西安 710000;2.渭南市东雷二期抽黄工程管理中心 陕西 渭南 714000)
前言
地震动频谱特性是指组成地震动各简谐振动分量的振幅和相位特征,频谱显示不同频率分量的强度组成和分布,直接反映了地震动的动力特性。描述地震动的参数主要包括幅值、频谱特性和持续时长,场地土层分析及结构抗震分析直接表现为对特定频率的放大或缩小,进而对建筑物造成危害,因而地震动频谱特性分析尤为重要。
一、相关理论
(一)短时傅里叶变换(STFT)
短时傅里叶变换变换以合适的窗函数截取信号,假定信号在每一个窗口内都是平稳的,然后采STFT变换处理每个窗口内的信号,以便确定其对应的频率,最后选择合适的窗口移动参数,沿着信号移动窗函数,便可得到信号的时频关系,STFT变换的定义为[1-2]:

式中,h(t)为地震信号;t为窗口函数g(τ)的中心时刻。
虽然STFT变换能够得到地震动时频关系,可实现对信号的局部时频分析,但其自身仍然存在一定的缺点:当窗函数g(τ)确定后,STFT变换的窗口的大小和形状在整个变换的过程中都不能发生改变。
(二)一维连续小波变换(CWT)
小波变换可以根据伸缩因子a和平移因子b进行自适应调节,小波基ψ(t)根据伸缩因子a和平移因子b进行变换,具有更好的适用性[3-4]。
设信号f(t)∈L2(R),L2(R)表示平方可积的实数空间,即能量有限的信号空间,ψ(t)为小波基函数:

式中:Ψ(ω)是ψ(t)的傅里叶变换结果;Cψ对每一个小波基函数是一个常数。满足该条件的一维连续小波变换为:

Morlet是一种常见的小波基函数,利用Morlet小波可以将信号的振幅和相位分开,它是一种复正弦单频调制高斯波,在时域和频域同时具有良好的分辨率,因此,被认为是分析非平稳地震信号最合适的小波。
Morlet小波时域、频域表达式分别为:
二、实场应用
地震动频谱特性对场地土层地震反应和结构抗震分析尤为重要,从日本强震观测台网 KiK-net 数据库中选取两类不同频谱特性的地震动,如表1所示,应用MATLAB编制小波程序,分别完成小波变换及傅里叶变换,进行对比分析说明两类地震动的特点。

表1 地震动基本信息
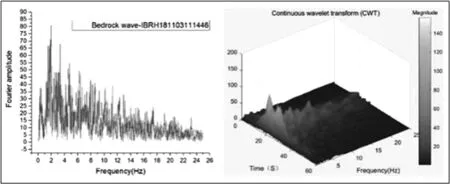
(a)001基岩波
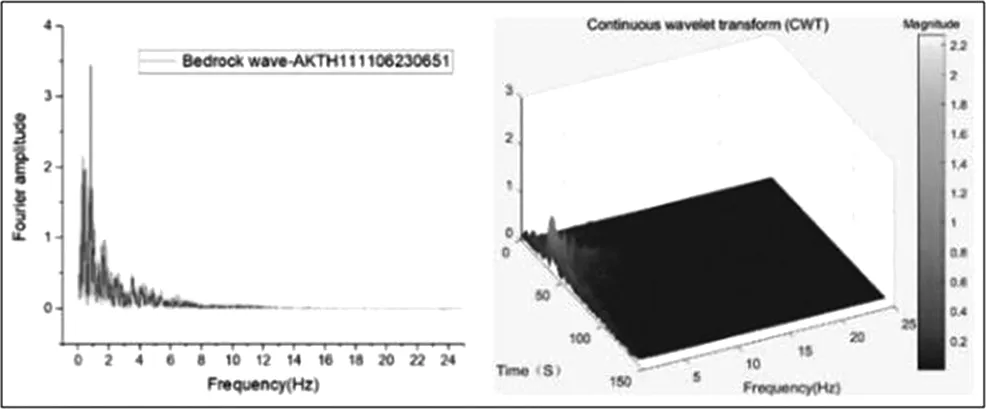
(b)002基岩波
由表1、图1可知,所选两类地震动具有明显的不同,前者基岩波频率分布相对均匀,覆盖频段较广,持时短60s,PGV/ PGA为0.076126,具有普通地震动特性;后者频率分布相对集中,卓越频率为1.1Hz左右,持时长140s,PGV/ PGA为0.2752108,具有长周期地震动特性,STFT变换在频域具有理想的分辨率,但时域表现不足,CWT变换在时域、频域均可得到理想的效果。
三、结论
本文首先完成短时傅里叶变换和一维连续小波变换的理论疏导,并利用MATLAB编制小波程序,选取两类实际地震动记录,分别进行STFT变换和CWT变换处理,完成对两类地震动的分析,结论如下:
1)长周期地震动相较普通地震动,频域内其低频更为丰富,能量更为集中,更易引起相应频段结构或土层发生共振破坏效应,工程应用中应予以重视;
2)Morlet基小波在时域和频域同时具有良好的分辨率,可以得到可靠的小波分析结果;
3)对比实场地震动的傅里叶变换和小波变换可知,地震动能量峰值对应的时域、频域基本一致,小波分析能够达到可靠的分析目的,可用于地震动频谱分析。

