基于组合模型的商品订单预测研究

(北京物资学院 北京 010000)

一、引言

随着电商行业的快速发展，电商在运营管理上面临越来越多的问题，其中重点突出的问题是商品订单量的库存计划不到位，商品短缺和库存积压制问题并存，导致资金短缺仓库利用率低，严重制约了电商公司长久发展。传统的订单预测分析通常采用时间序列、季节性预测等方法，这种方法使用的数据量小，比较适合传统销售模式下的订单预测问题。针对电商订单的海量数据特点，使用传统的预测模型已不能满足要求。近几年，机器学习逐渐兴起，被广泛地应用到预测领域，如机场能见度预测[1]、金融风险预测[2]等。本文考虑到订单量数据线性与非线性的特点，把传统的预测方法与机器学习的方法结合建立组合模型，实现对商品订单的预测分析。

二、组合预测模型原理

在组合模型的研究上，丁宏飞[3]提出多模型融合预测算法对快速路行程时间进行预测，杨波、吴涵[4]建立趋势曲线预测模型、回归预测模型及灰色预测模型的物流需求单项预测模型，建立了组合预测模型，并以重庆空港物流园为例进行应用。综上所述，组合预测模型在一定程度上可以有效地提高预测精度。本文采用的组合模型思路是将一系列不同模型的预测结果通过某种规则汇集到一起，从而得到更好的预测结果。这种组合的关键在于模型的多样性，如果各个模型的偏差在不同方向上，那这些偏差就会彼此抵消，组合结果会更加稳定、更加准确。考虑到电商商品订单数据的线性和非线性因素，本中选择了选择BP神经网络、XGBoost模型和ARIMA时间序列组成组合预测模型，每个模型的权重通过将Shapley值法[5]确定。

综上所述，组合预测模型原理如图1所示：

图1 组合预测模型原理图

三、实验与分析

(一)实验数据

实验使用的数据为亚马逊店家后台下载的某商品2018年5月-12月以周为单位的共30条数据，共240个数据。该数据共包含了7个解释变量，分别为登陆次数、登陆人数、成交笔数、收藏人次、浏览次数、流量和成交金额。在实验中，本文假设在预测第t天的订单量时，第t天之前的数据已知。数据集的划分为前28周的数据为训练集，后2周的数据为预测集。

(二)ARIMA模型预测

ARIMA模型建立需要通过：数据平稳性判别、非平稳序列差分处理、模型识别与定阶、选定模型拟合、检验模型的预测准确性和使用模型进行预测等步骤。对比出最优模型为ARIMA(4，1，0)。

(三)BP神经网络预测

数据集中前28周数据用于模型训练和建立，通过该数据对模型进行交叉验证并确定最优模型。用训练好的模型对后两周的订单进行预测。参数设置如表1：

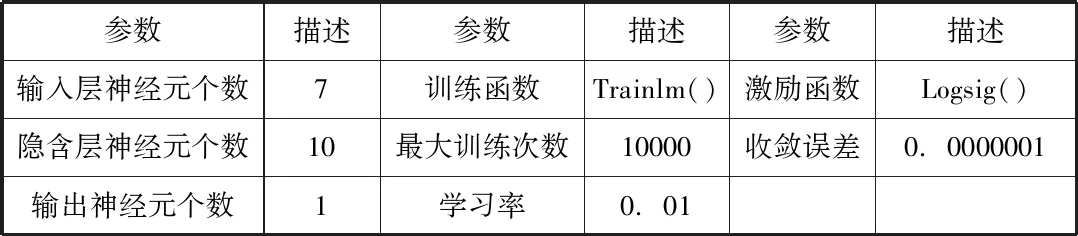
表1 BP神经网络参数设置

(四)XGBoost模型预测

模型的建立主要为调参，通过大量实验，选出模型的最优参数。参数设置如表2：

表2 XGBoost参数设置

(五)组合模型预测

在训练集上使用这三种模型进行训练，得到训练集上的拟合值，计算拟合值与实际值之间的平均相对偏差值(MRD)，其中ARIMA的MRD%为14.66，BP神经网络的MRD%为10.09，XGBoost的MRD%为5.29。经过计算，组合模型总平均相对偏差MRD%为10.01。根据Shapley值的概念，参与组合预测模型总误差分摊的“合作关系”的成员为N={1，2，3}，它的所有子集的集合的平均相对偏差值分别为E{1}、E{2}、E{3}、E{1，2}、E{2，3}、E{1，3}、E{1，2，3}，其数值的大小为该子集所包括向量的均值大小如表3所示。

表3 子集误差值

按照公式的Shapley值的计算方法，求出各成员的Shapley值为E1=6.82、E2=3.40、E3=-0.20。根据权重公式(公式1)

(公式1)

计算各单一预测方法在组合模型中的最终权重为：W1=0.16、W2=0.33、W3=0.51.

故最终组合预测模型为公式2：

Y=0.16Y1+0.33Y2+0.51Y3

(公式2)

四、预测结果分析

根据上文的单一模型和组合模型对未来两周的订单进行预测，计算各模型在每周的平均相对偏差和偏差均值，统计结果如表4所示：

表4 各模型的预测结果及相对偏差统计表

由上表可以看出，在预测结果上组合模型的预测效果最好，平均相对偏差仅为2.49%，但也出现了很大的波动，即第一期预测很好，但第二期效果较差。BP神经网络表现较为稳定，但效果没有组合模型显著。组合模型相比于单一模型有明显提高。各模型MRD波动情况如图2所示，ARIMA模型的误差波动最激烈，预测表现最差；BP神经网络表现较好，除了几个异常点外，误差基本维持在10%以内；XGBoost模型没有明显波动，在预测后期相比预测前期表现略差；组合模型中有几个最小误差也出现在该模型中，说明组合模型能够很好的修正单一模型的波动，使误差波动更稳定。

图2 平均相对偏差MRD波动图

五、结论

针对电商商品订单的线性与非线性特征，本文选择了在线性数据上有优势的ARIMA模型和适用于非线性数据的BP神经网络和XGBoost模型建立组合模型。预测结果表明，相比于单一模型，组合模型能够很好的修正单一模型的波动，使误差波动更稳定，在预测准确率上有更好的表现。