基于无模型自适应的粗煤泥分选控制系统研究
刘晓红,韦鲁滨,于海洋
(1.中国矿业大学(北京)化学与环境工程学院,北京 100083;2.山东交通学院,山东 济南 250357)
煤炭洗选加工是目前煤炭清洁高效利用的重要技术手段,按照“清洁、低碳、高效、集中”的原则,预计全国原煤入洗率在2020将达到75%以上。在粗煤泥分选设备中,干扰床分选机(TBS)因其结构、分选工艺简单、处理量大、介质消耗低被广泛应用于动力煤和炼焦煤等类型的选煤厂[1-3]。
目前,选煤厂粗煤泥分选机采用的都是传统PID控制、模糊PID控制及智能控制等。传统PID控制容易受到模型摄动、环境干扰的影响,导致PID控制器难以维持一致的控制性能,参数需要再次调节才能使系统稳定。模糊PID控制及智能控制往往依赖于被控对象精准的数学模型,粗煤泥分选机属于复杂的控制系统,难以建立其被控对象精准的数学模型,并且控制效果受模型摄动、环境扰动等不确定性的影响,导致常规数学模型导向的控制策略自适应性较差,难以保证控制系统的鲁棒性和稳定性。综上,常规基于数学模型的控制方法在工程实践中难以达到理想控制效果。
针对上述问题,本文采用一种针对非线性系统设计的无模型自适应控制方法(model free adaptive control,MFAC)。该方法不考虑被控对象数学模型,而是通过系统输入和输出(input/output,I/O)数据进行控制器设计,且具有控制结构简单、计算速度快的优点。无模型自适应控制的理论在电力、能源、化工等领域已经有较多应用。钱虹等[7]针对火电厂过热蒸汽温度控制,设计了自适应模型预测控制器,通过对不同模型的在线辨识和控制表明:自适应控制与普通模型预测控制器相比,调节时间大幅缩短,超调量得到了减小或消除,动态性能有了较大的改善;韩学烁[8]基于无模型控制算法在制冷机组中的应用进行研究,提出了改进的无模型自适应控制方法,并最终在制冷系统的二阶模型上对控制方案进行了仿真比较研究,验证了新型控制方法的有效性;刘斌[9]基于无模型自适应控制器在锅炉控制系统中的应用进行研究,通过仿真得出无模型自适应控制器在锅炉系统的应用中更具优势,其响应更加迅速,系统也更加稳定;黎丹[10]基于偏格式的无模型自适应控制算法对锅炉汽包水位控制研究,并通过仿真对比PID算法、无模型自适应算法及改进的无模型自适应算法的控制效果,验证了偏格式的无模型自适应控制算法的可行性。综上,无模型自适应控制在能源、化工、炼油等工业控制领域获得了应用,但是目前在煤炭分选控制领域的研究较少[11-12]。
本文针对粗煤泥分选系统难以建立被控对象精准数学模型的问题,采用紧格式的无模型自适应控制方法进行控制器设计,并通过与传统PID、模糊PID控制进行仿真对比,表明无模型自适应控制可以在粗煤泥分选过程中,减少因控制系统超调量过高而造成的跑粗现象,并提高了系统的抗干扰能力,改善了精煤产品的质量。
1 粗煤泥分选控制系统方案
粗煤泥分选机的分选效果与原煤煤质、分选工艺参数设定及关键参数的精准控制密切相关。主要的影响因素包括:入料粒度与浓度、上升水流流速、给水流量与压力、干扰床层密度设定等。其中入料的粒度和浓度、上升水流流速、给水流量与压力均为分选开始前进行设定。而干扰床层密度则在粗煤泥分选过程中,根据产品灰分的要求进行精准控制。干扰床层密度的变化对分选效果和精煤质量影响很大,因此对干扰床层密度的控制尤为重要。
粗煤泥分选机分选控制系统原理如图1所示。在粗煤泥分选机不同位置设置两台FMX型密度计,对分选机干扰床层密度和颗粒松散度进行连续监测,控制系统将监测值与设定值进行对比。
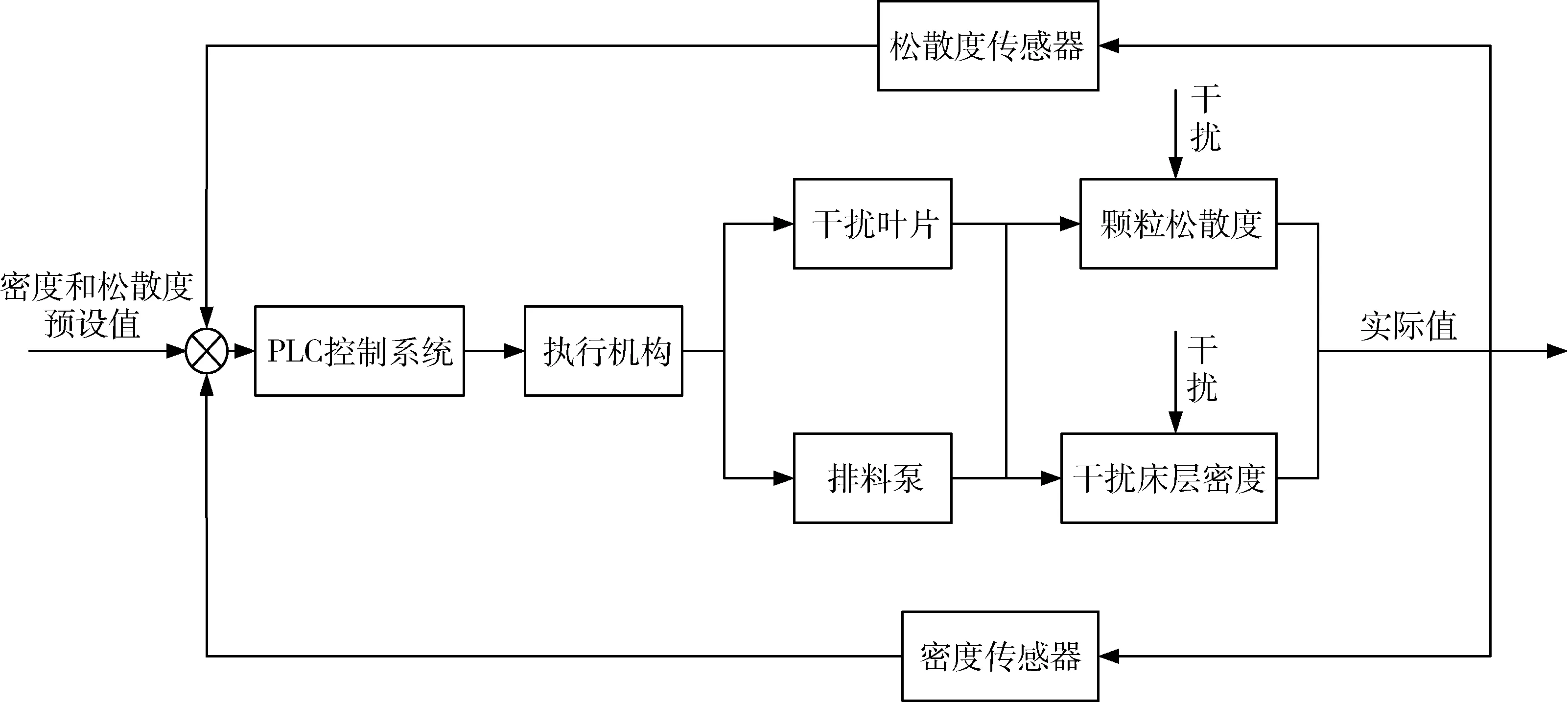
图1 分选控制系统原理图Fig.1 Structural diagram of sorting control system
当分选机内颗粒松散度高于预设值时,控制系统将通过控制变频电机减少干扰叶片转速,减少干扰。反之,则增加变频电机干扰叶片转数,加大干扰。
当分选机干扰床层密度高于预设值时,控制系统将增加分选机底部旋转刮板的转数,将沉降的分选机底部的矸石颗粒刮到排料管附近,辅助排出矸石以减少干扰床的密度直至预设值。反之,则增加下部干扰叶片转数,改变沉降穿过干扰床层的矸石和煤颗粒的运动方向,减缓矸石颗粒的沉降速度,使干扰床层的密度升高到预设值。
2 无模型自适应控制律
2.1 无模型自适应控制原理
粗煤泥分选机属于复杂的控制系统,具有非线性、不确定性和时变性的特征。其控制难点体现在:①难以建立其被控对象精准的数学模型,导致许多基于数学模型的控制方法在工程实践中难以应用;②受模型摄动、环境扰动等不确定性的影响,常规数学模型导向的控制策略自适应性较差,难以保证控制系统的鲁棒性和稳定性。综上,常规基于数学模型的控制方法在工程实践中难以达到理想控制效果。
无模型自适应控制方法很好地符合上述要求,是一种针对非线性系统设计的控制方法。其工作原理:控制器的输出参数为被控对象的控制输入参数,系统根据输出参数对控制输入参数进行跟踪,完成时变参数的在线辨识,控制器依据辨识得到的新时变参数进行调节,持续反复的参数辨识和控制器调节,使得控制器的性能逐步增强。基本原理见图2。
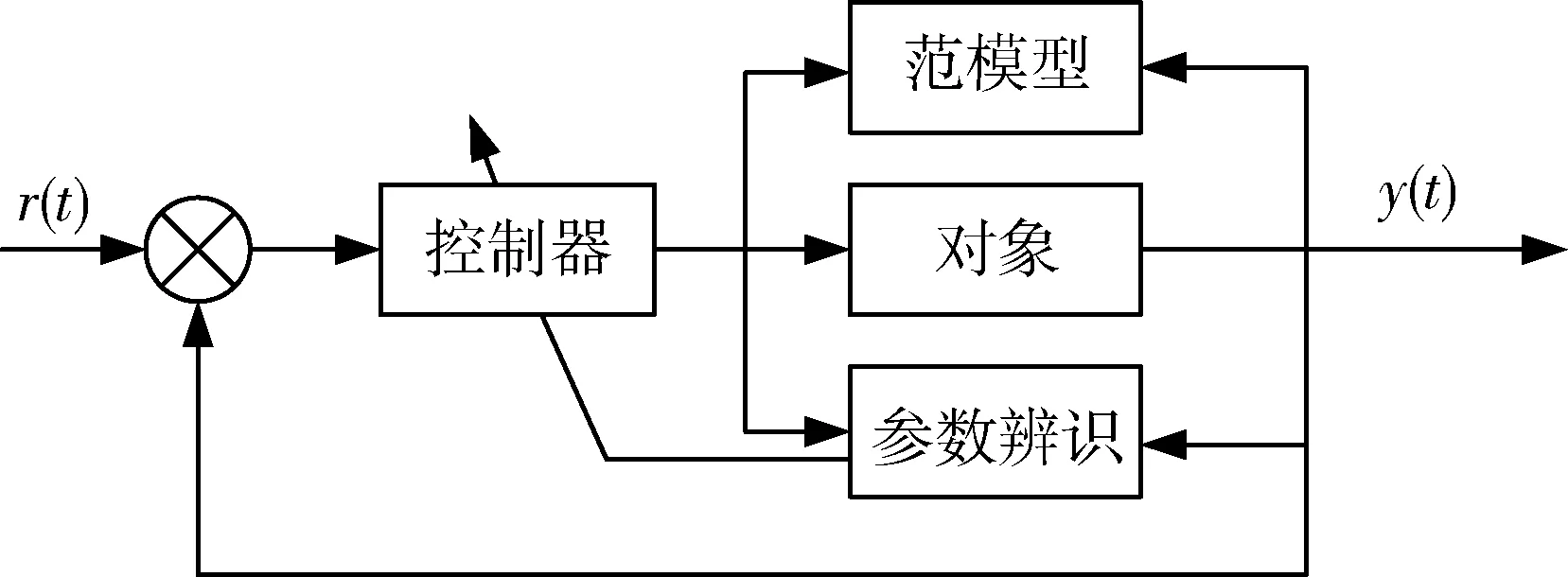
图2 MFAC控制原理图Fig.2 Schematic diagram of MFAC control
2.2 基于紧格式的无模型自适应控制律
一般离散时间非线性系统的动态线性化技术,通常有三种动态线性化格式:紧格式线性化方法(compact form dynamic linearization,CFDL)、偏格式线性化方法(partial form dynamic linearization,PFDL)和全格式线性化方法(full form dynamic linearization,FFDL)。针对粗煤泥分选系统外部干扰因素多的特点,本文采用紧格式动态线性化MFAC(compact form dynamic linearization based MFAC,CFDL-MFAC)方法,探讨不确定性影响下粗煤泥分选系统的干扰床层密度控制问题。
2.2.1 紧格式线性化方法
一般单输入单输出非线性离散时间系统计算见式(1)。
y(t+1)=f(y(t),y(t-1),…,y(t-ns),u(t),
u(t-1),…,u(t-nu))
(1)
式中:y(t)、u(t)为t时刻被控系统的输出和输入;ns、nu为被控系统输出和输入的未知阶数;f(…)为未知的非线性函数。
对上述系统作如下假设。假设1:式(1)的系统输入输出可观可控;假设2:f(…)对系统控制输入u(t)的偏导数存在且连续;假设3:式(1)的系统对于任意的t和Δu(t)≠0,存在一个大于0的常数a,见式(2)。
|Δy(t+1)|≤a|Δu(t)|
(2)
式中:Δy(t+1)=y(t+1)-y(t);Δu(t)=u(t)-u(t-1)。
式(1)的系统满足以上三个假设条件,则当Δu(t)≠0时,存在一个伪偏导数φ(t),见式(3)。
Δy(t+1)=φ(t)Δu(t)
(3)
根据伪偏导数定理,得到基于紧格式线性化的动态线性化模型,见式(4)。
y(t+1)=y(t)+φ(t)Δu(t)
(4)
引入一个控制输入准则函数对Δu(t),限制输入量的变化,见式(5)。
J[u(t)]=[y*(t+1)-y(t+1)]2+
λ[u(t)-u(t-1)]2
(5)
式中:λ为权重因子;y*(t+1)为t+1时刻系统设定值;y(t+1)为t+1时刻系统实际输出值;λ[u(t)-u(t-1)]2可以限制Δu(t),并可以克服稳态误差。
2.2.2 紧格式动态线性化MAFC方案
基于紧格式动态线性化无模型自适应控制方案,见式(6)。

(6)
式中:ρt为步长序列;λ为权重因子,不仅能控制Δu(t)的变化,限制了非线性时变系统由动态线性系统的替代范围,有效保证系统泛模型动态线性化的要求;且可以防止式(4)出现分母为零。
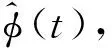
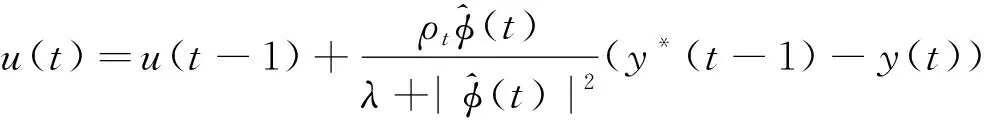
(7)
从式(7)可以看出控制律只与受控系统的输入输出有关。
伪偏导估计准则函数见式(8)。
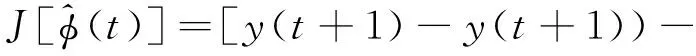

(8)

联合式(3)和式(8),根据最优条件,得到伪偏导的估计算法,见式(9)。
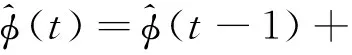

(9)
无模型自适应控制系统的设计,无需考虑受控系统的数学模型和阶数,只根据系统输入输出设计控制系统,因此适用于粗煤泥分选系统。
根据以上推导,得到基于紧格式的无模型自适应控制率,计算见式(10)。
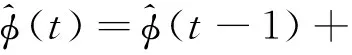

(10)

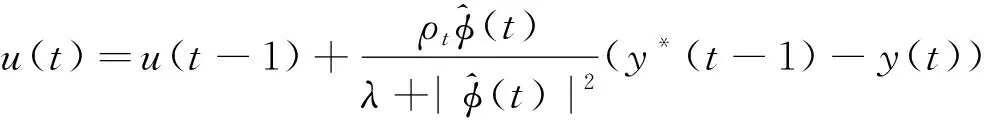
(11)
3 系统控制器设计
本节主要以干扰床层密度的控制系统作为被控对象,分别采用常规PID、Fuzzy-PID和MFAC控制进行粗煤泥分选系统控制器的设计。
3.1 常规PID和Fuzzy-PID控制器
常规PID的控制律,计算见式(12)。
u(k)=
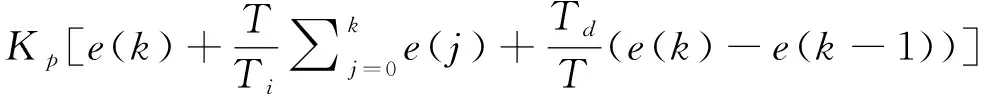
(12)
式中:Kp为比例系数;Ti为积分系数;Td为微分系数;T为采样周期;e(k)=y×(k)-y(k)为期望输出y×(k)与系统实际输出值y(k)之间的跟踪误差。
为研究问题方便,忽略实际生产中一些次要的影响因素,通过简化的粗煤泥分选控制系统模型,可得干扰床层密度传递函数,计算见式(13)。
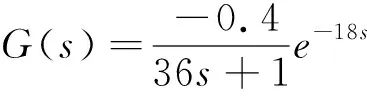
(13)
通过临界比例度法,并根据N-Z规则表可以计算PID控制器的参数,计算见式(14)~(16)。

(14)

(15)
Td=0.5τ=0.5×18=9
(16)
Fuzzy-PID控制器模糊控制部分的参数,通过模糊论域与基本论域之间的比例关系,可得式(17)~(19)。
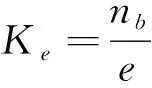
(17)

(18)

(19)
式中:e为系统误差;ec为误差的变化率;u为控制器的输出控制量;[-nb,nb]为系统误差e的精确量。
3.2 无模型自适应控制器设计
基于MATLAB/Simulink提供的S-function函数模板,采用M语言进行S-function函数的编写。根据式(10)和式(11)进一步整理基于紧格式线性化的MFAC控制器的M文件书写格式函数形式,见式(20)~(22)。
phi(t)=phi(t-1)+Eta×d_u1(t-1)/
(Mu+abs(d_u1(t-1))2)×
(d_y(t)-phi(t-1)×d_u1(t-1))
(20)
phi(t)=phi(1),若abs(phi(t))≤epsilon或
abs(d_u1(t-1))≤epsilon
(21)
u1(t)=u1(t-1)+pho×phi(t)/
(lambda+abs(phi(t))2)×e1(t)
(22)
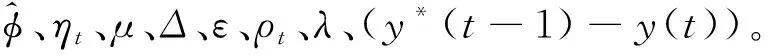

图3 无模型自适应模块结构框图Fig.3 MFAC module structure block diagram
4 系统性能仿真对比分析
4.1 系统跟踪性能仿真分析
设置分选机的床层密度为1.4 g/cm3,即Step=1.4。分别对PID控制系统、Fuzzy-PID控制系统和MFAC控制系统进行仿真,结果如图4所示。
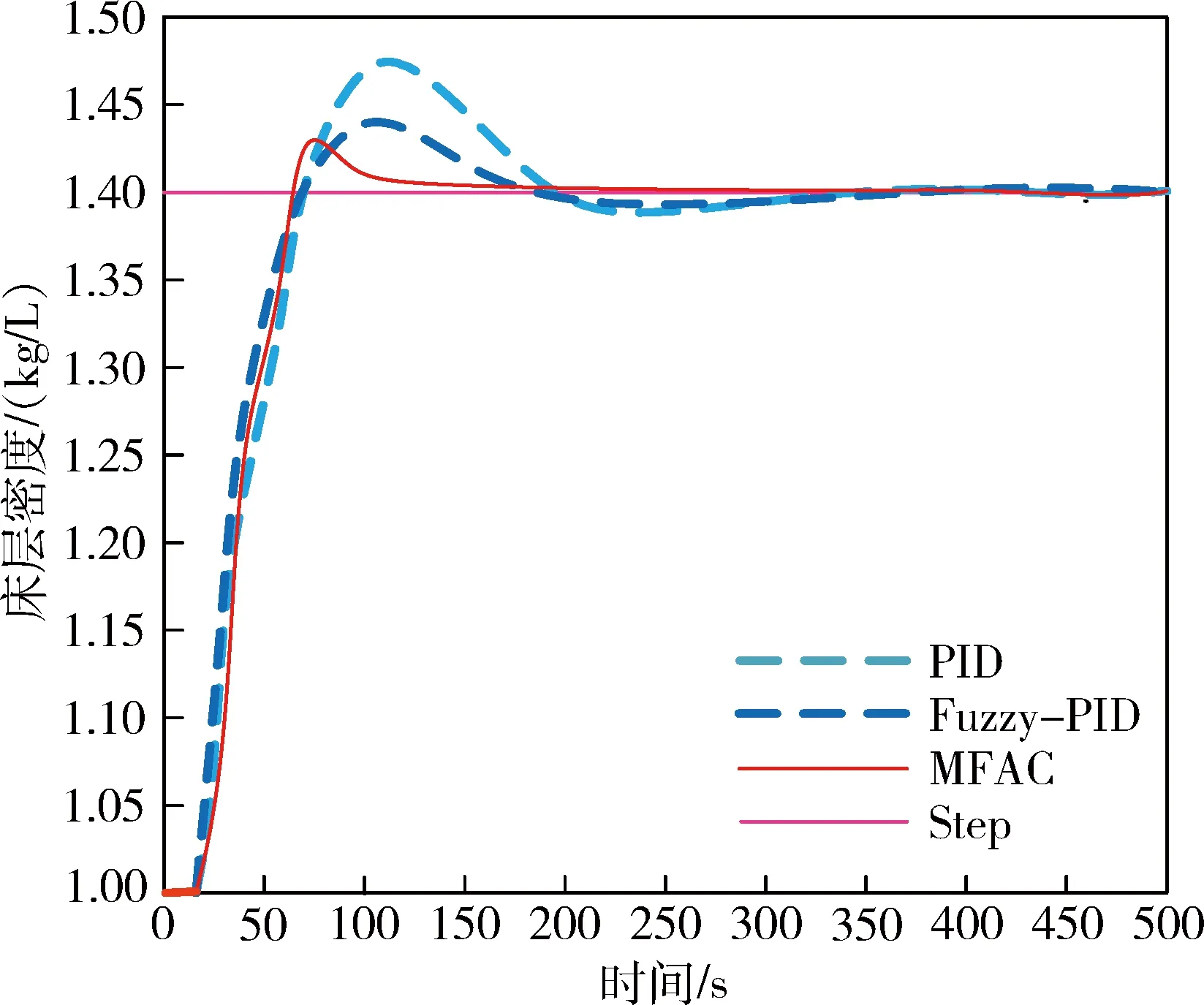
图4 MFAC、PID和Fuzzy-PID的跟踪性能对比图Fig.4 Comparison of tracking performance between MFAC,PID and Fuzzy-PID
由图4可知,干扰床层密度跟踪超调量PID控制系统最大,Fuzzy-PID控制系统次之,MFAC控制系统的超调量最小。PID控制系统和Fuzzy-PID控制系统对床层密度跟踪均出现波动现象,且用时较长。MFAC控制系统对床层密度跟踪的用时最短,在140 s左右实现了对床层密度的跟踪。因此,MFAC控制系统跟踪性能优于PID和Fuzzy-PID控制系统。
4.2 系统适应能力仿真分析
保持分选控制系统其他参数不变,改变单一环境变量因素,观察不同控制环境变化下PID控制、Fuzzy-PID控制和MFAC控制的适应能力。首先,将增益由0.4改变为0.5,仿真结果如图5所示。
由图5可知,系统增益的改变在上升阶段,PID控制、Fuzzy-PID控制和MFAC控制变化的特性并未改变,但是明显三者的超调量都增加了,达到超调最高峰的时间缩短,PID控制的最大超调量已经达到1.48,综上,MFAC控制的表现最优。
然后,将系统的惯性时间由36 s改变为50 s,其他控制因素不变,观察PID控制、Fuzzy-PID控制和MFAC控制的仿真结果,如图6所示。

图5 增益改变时MFAC、PID及Fuzzy-PID仿真结果对比图Fig.5 Comparison of simulation results of MFAC,PID and Fuzzy-PID when gain changes

图6 惯性时间改变时MFAC、PID及Fuzzy-PID仿真结果对比图Fig.6 Comparison of simulation results of MFAC,PID and Fuzzy-PID when inertia time changes
由图6可知,惯性时间的改变使得PID控制、Fuzzy-PID控制和MFAC控制达到最大超调量和实现稳定跟踪的时间均出现增加现象,但MFAC控制实现稳定控制时间增加的时间不明显。对比图5,系统惯性时间改变各个控制系统的超调量小于增益改变下控制系统的超调量。系统惯性时间改变MFAC控制的性能依然优于PID控制和Fuzzy-PID控制。
最后,改变系统的滞后时间由18 s改变为20 s,其他控制因素保持不变,观察PID控制、Fuzzy-PID控制和MFAC控制的仿真结果,如图7所示。
由图7可知,系统滞后时间的增加使得系统的控制难度增加,Fuzzy-PID控制的超调量有所增加,PID控制和MFAC控制的超调量增加不太明显。PID控制、Fuzzy-PID控制和MFAC控制到达最大超调的时间和实现稳定跟踪的时间全部增大,且系统实现跟踪后MFAC也略有波动,出现了一次较小震荡。总体,MFAC控制系统的表现依然优秀。
4.3 系统抗干扰能力仿真分析
为了验证MFAC的抗干扰性能,在系统跟踪阶段对系统施加5 s,强度为3%的干扰,PID控制、Fuzzy-PID控制和MFAC控制的仿真结果,如图8所示。
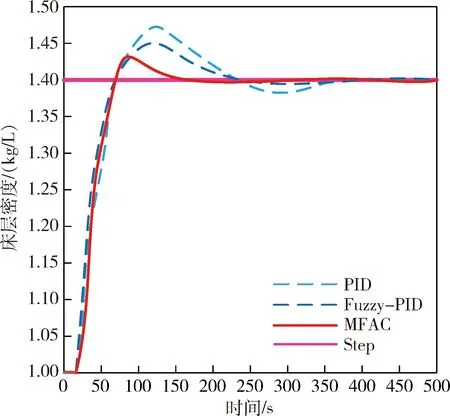
图7 滞后时间改变时MFAC、PID及Fuzzy-PID仿真结果对比图Fig.7 Comparison of simulation results of MFAC,PID and Fuzzy-PID when the lag time changes
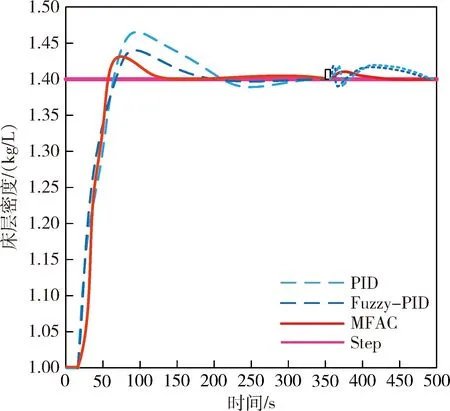
图8 MFAC、PID及Fuzzy-PID抗干扰仿真结果对比图Fig.8 Comparison of simulation results of MFAC,PID and Fuzzy-PID anti-jamming
由图8可知,在干扰信号源的干扰下,PID控制、Fuzzy-PID控制对干扰反应出现了强烈振荡,且在干扰后再次实现稳定跟踪的调整时间较长。MFAC控制系统在干扰下也出现了超调但未出现振荡现象,且能多再次实现稳定跟踪。
综上,在粗煤泥分选过程中,采用无模型自适应控制方法设计的控制器,系统超调量小,跟踪用时短,可以有效地减少因控制系统超调量过高而造成的跑粗现象;并且相比传统PID控制和Fuzzy-PID控制,其适应能力和抗干扰能力更强,稳定性更优。
5 结 语
针对粗煤泥分选系统难以建立被控对象精准数学模型的问题,采用紧格式的无模型自适应控制方法,提出一种基于紧格式的无模型控制方法,并通过与传统PID控制、Fuzzy-PID控制进行仿真对比分析,结果表明无模型自适应系统可以有效地减少因控制系统超调量过高而造成的跑粗现象,并提高系统的抗干扰能力,改善精煤产品的质量。
——人-时间资料率比分析与SAS实现

