基于蚁群算法与参数迁移的机器人三维路径规划方法

刘 可 李 可 宿 磊 王 琨 张秋菊

(1.江南大学江苏省食品先进制造装备技术重点实验室， 无锡 214122; 2.江南大学机械工程学院， 无锡 214122)

0 引言

机器人在农业采摘、分拣、码垛等方面的广泛应用极大地促进了农业机械化发展。机器人运动轨迹规划是机器人学研究的一个重要方面，合理的运行轨迹可以使机器人快速准确地完成指定作业任务。机器人的三维路径规划是指按照任务要求，机器人在复杂空间环境中按照某种规则寻找出从起点到终点的一条路径[1-2]。目前常用的机器人三维空间路径规划算法有人工势场法[3-5]、A*算法[6-8]、模糊逻辑法等[9]。人工势场法是在空间中放置一个虚拟力场代替障碍物，通过力场的排斥与吸引控制机器人运动，这种算法在障碍物与目标点较近时容易陷入局部最优解。A*算法可以适用于高维空间，但是随着维数的增加，很难达到算法的时空要求。模糊逻辑算法将专家知识转换为控制信号，符合人类思维习惯，但模糊规则很难总结，应变性较差。

蚁群算法[10]在解决机器人三维路径规划问题上显示出良好的适应性，但与其他启发式优化算法一样，其算法参数的选择对优化结果有较大影响。蚁群算法传统的参数选取方法主要是经验选择法、实验试凑法、正交实验设计法等。传统的参数选择方法具有一定的局限性，经验选择法依赖于知识和经验，实验试凑法费时、低效，正交实验设计法没有考虑参数间的耦合性。近年来，国内外陆续有学者使用一些智能优化算法对蚁群算法的参数进行选取，如遗传算法(Genetic algorithms, GA)[11]、粒子群算法(Particle swarm optimization, PSO)等[12]。然而这些方法又引入了更多的参数选择问题，如GA算法中的交叉算子、变异算子，PSO算法中的惯性权重、学习因子等，使得整个寻优算法更加复杂。

蚁群算法参数的不确定性和各参数间的耦合性，使得如何确定蚁群算法的最优参数成为一个重要问题。迁移学习是近年来提出的一种新的机器学习方法，可以将在源领域和源任务中认知和学习的信息应用到目标领域和目标任务，完成或者改善目标任务的学习效果。在工程实践中，为每个任务收集数据或者寻找参数所需时间成本极大，甚至是不可实现的，因此从以往任务中迁移已有知识、进而解决目标任务是十分必要的。使用迁移学习中的参数迁移方法可以将已有的参数知识引入到新任务中，使相似领域中的参数信息可以有效重用。LAWRENCE等[13]提出了一种基于高斯过程的多任务信息向量机，通过共享多任务相同的高斯先验知识来学习高斯过程参数。洪佳明等[14]提出了基于领域相似性的迁移学习方法。YOAV等[15]提出根据目标任务在模型迁移网络中的位置确定新目标任务的模型参数。许夙晖等[16]提出了基于极限学习机参数迁移的域适应算法，使目标域的极限学习机分类器参数最大限度与源领域的分类器参数分布相同。

针对蚁群算法在机器人三维路径规划中的参数寻优问题，本文采用参数迁移[17]的方法对蚁群算法进行参数优化，降低算法复杂性，利用先验知识有效解决蚁群算法进行三维路径规划时的参数选择问题。

1 路径规划

1.1 三维环境建模

环境建模可以将真实的三维环境用数学模型代替，其建立方法对路径规划算法的时效性有很大影响。机器人在复杂工作环境内作业，完成码垛、采摘等工作，环境模型的建立有多种方法。本文采用山峰式环境模型模拟机器人工作环境，将真实的机器人三维环境用抽象的山峰图形表示。为简化之后的蚁群算法路径规划，以机器人自身基坐标系为基础，建立环境模型坐标系OXYZ。

在建立坐标系后，还需对环境模型栅格化[18-20]。栅格化是将机器人运行空间沿X、Y、Z方向分解为多个大小相同的网格，每个网格就是一个单元。将环境模型进行划分时，对每个单元设置标识，根据单元格内是否有障碍物，分为填充栅格、未填充栅格、半填充栅格。为了机器人运行过程中的安全，将半填充栅格与填充栅格标记为不可通行栅格，未填充栅格标记为可通行栅格。不可通行栅格取值为0，可通行栅格取值为1。经过处理后的机器人三维环境模型就可以用一个只有0和1的三维矩阵表示。

图1为机器人实际工作环境，图2为所建立的三维环境模型。将图1工作空间中的其他设备与障碍物以山峰代替。图2中曲面表面为机器人环境轮廓，曲面以下为机器人工作环境中的障碍物。

图1 机器人工作环境Fig.1 Robot working environment

因为机器人末端执行器在运行时会夹持工件或工具，需要与障碍物保持一定的安全距离，所以需要对环境模型进行扩张处理，增加障碍物高度，即在原地图的基础上，Z方向每单元增加一定高度H。

图2 机器人三维环境模型Fig.2 Robot 3D environment model

机器人三维路径规划的本质就是在满足一定约束的情况下找出环境中有效的最优路径。采用栅格法建立的环境模型，将机器人末端执行器的可通过区域、不可通过区域简化为栅格，那么机器人的三维路径规划问题就转变为在一个可通过栅格集合中寻找一个满足规划要求的栅格子集问题，从而得到符合要求的最短路径。

1.2 蚁群算法参数分析

蚁群算法主要有状态转移规则、信息素更新规则两个过程，其主要运行参数为α、β、ρ、Q，其具体控制作用在以下公式中体现

(1)

τij(t+1)=ρτij(t)+Δτij

(2)

(3)

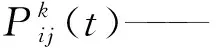
τij(t)——在路径ij上的残留信息素

ηij——点j处对i处的启发值

α——残留信息素参数

β——启发式因子参数

N——蚂蚁处于点i时下一步的可行点集

Δτij——时间t到t+1的新增信息素值

ρ——信息素衰减系数

Lk——蚂蚁搜寻的路径长度

Q——新增信息素强度

参数ρ的值直接影响路径规划效率，ρ过大，蚁群算法的全局搜索能力会提高，收敛速度变慢；ρ过小，全局搜索能力变小。

1.3 三维路径点选取原则

为了简化算法设计，结合机器人路径规划的最短路径和最小时间要求，将蚂蚁的运动方式简化为分层前进方式，对应到环境模型中，X方向每次前进一层到达下一平面的某一可行点，在下一平面的Y方向和Z方向进行路径点搜索，寻找可行路径点，以此类推，最后到达目标点，得到一条路径。蚂蚁运动包括前进，左、右移动，上、下移动5种方式，在路径规划算法中，蚂蚁的运动就对应着机器人末端执行器的移动。对应这种简化的机器人运动方式，蚂蚁从平面Ra移动到平面Ra+1时，允许左移或者右移yc(yc={0，1，2})，允许上移或下移zc(zc={0,1,2})，路径点选取方法如图3所示。

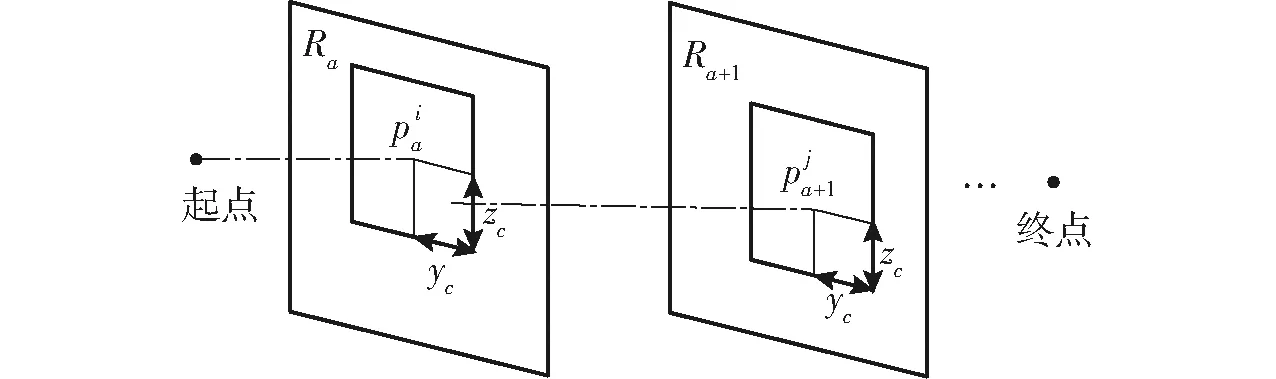
图3 路径点选取原则Fig.3 Path point selection principle

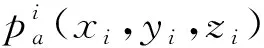
(2)计算可行点集p中任一点的启发值ηij。

(4)

式中S——根据式(1)给出的概率分布所选出的最大值

q0——区间[0,1]中的常数

q——区间[0，1]中均匀分布的随机数

1.4 启发式函数

启发式函数是机器人三维路径规划算法中的重要部分，直接影响到算法能否进行快速、高效的路径规划。路径中所需要考虑的各种因素都需要在路径规划算法中体现。本文的机器人三维路径规划算法要求安全、路径最短、时间最少和运动平滑性。根据算法要求，任一点的启发值公式为

η(x,y,z)=S(x,y,z)[D(x,y,z)]w1[F(x,y,z)]w2

(5)

式中S(x,y,z)——安全因素，考虑下一点是否可达

D(x,y,z)——距离时间因素，要求所规划路径尽可能短，时间尽可能少

F(x,y,z)——运动平滑因素，要求所规划的路径尽可能地平滑，避免出现拐点引起机器人抖动

w1、w2——权重

w1、w2取值由实验测试获得，本文使用正交实验法，当w1=10、w2=5时，路径寻优效果较好。

考虑机器人路径中的安全因素S(x,y,z)，在三维环境建模时，对栅格的标记将栅格分为不可通行栅格集N{p1,p2,…,pi}和可通行栅格集Y{p1,p2,…,pj}，S(x,y,z)的取值为

(6)

距离时间因素D(x,y,z)考虑路径尽可能短，时间尽可能少。因为机器人匀速运动，所以路径最短即代表所用时间最小。使用D(x,y,z)表示下一平面上可行点集中任意一点(x,y,z)到出发点(xs,ys,zs)的距离，值越大表示选择该点的路径总长度越短。D(x,y,z)的计算公式为

(7)

式中K1——常数

机器人在实际运动过程中如果路径较为曲折，那么其自身的减速器等硬件容易出现震颤等问题，因此在路径规划算法中需要考虑其路径的平滑性，期望其尽可能的在同一高度运行。因此，本文在启发函数中加入运动平滑因素F(x,y,z)，计算公式为

(8)

式中zG——下一平面可行点集中的任一点的Z方向坐标值

K2——常数

2 参数迁移

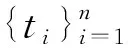
2.1 迁移矩阵

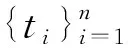
fi,j=(lj-li,j)/lj

(9)

式中li,j——蚁群模型mj在使用参数组pi时规划出的路径长度

lj——蚁群模型mj在使用参数组pj规划时的路径长度

迁移性能参数fi,j可以衡量任务mi的参数迁移到任务mj时的性能，并且两个任务间的迁移具有不相等性，即fi,j≠fj,i。迁移性能参数fi,j≥0时，代表正向迁移，迁移的任务参数比原始参数有更好的性能。fi,j<0代表负向迁移，迁移后寻找的路径变差。

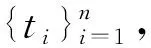
所有源任务之间的迁移性能参数可以得到迁移矩阵An，An=[ai,j]的定义为

(10)

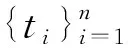
2.2 扩展迁移矩阵

G=(P,An)可以描述源任务之间的迁移性能，将其进行扩展使其包括目标任务。目标任务集为包括目标任务tn+1在内的集合，目标参数集为包含目标任务参数组的集合。对于目标任务tn+1，为其随机分配一组参数pn+1=(αn+1,βn+1,ρn+1,Qn+1)，计算各源任务对目标任务的迁移性能参数=(1,2,…,n)。

(11)

2.3 目标任务的最优参数获取

(12)

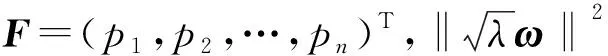
(13)

求解权值矩阵W可得

W=(QTQ+)-1QTF

(14)

求出权值矩阵W后，利用映射函数=W求出。则该映射函数矩阵的第n+1行即为目标任务求得的最优参数组n+1。

本文所提出的基于蚁群算法参数迁移的机器人三维路径规划方法整体思路如图4所示。

图4 基于蚁群算法参数迁移的机器人三维路径规划算法流程图Fig.4 Flow chart of robot 3D path planning method based on ant colony parameter transfer algorithm

3 仿真实验及分析

3.1 仿真环境设置

以Fanuc LR Mate200iD型机器人为对象，对其末端执行器轨迹进行路径规划仿真，机器人如图5所示。Fanuc LR Mate200iD型机器人是6自由度串联工业机器人，其控制器为Fanuc R-30iB Mate型。

图5 Fanuc LR Mate200iD型机器人Fig.5 Fanuc LR Mate200iD robot

在进行机器人仿真作业任务时，机器人控制系统需要先得到末端执行器的规划路线，根据逆运动学解出机器人6个关节的关节角，驱动机器人模型在仿真环境中完成指定任务动作，机器人三维仿真模型如图6所示。为验证本文提出的基于蚁群算法参数迁移的机器人三维路径规划算法的有效性，使用三维环境模型地图进行仿真实验。

图6 机器人三维模型Fig.6 Robot 3D model

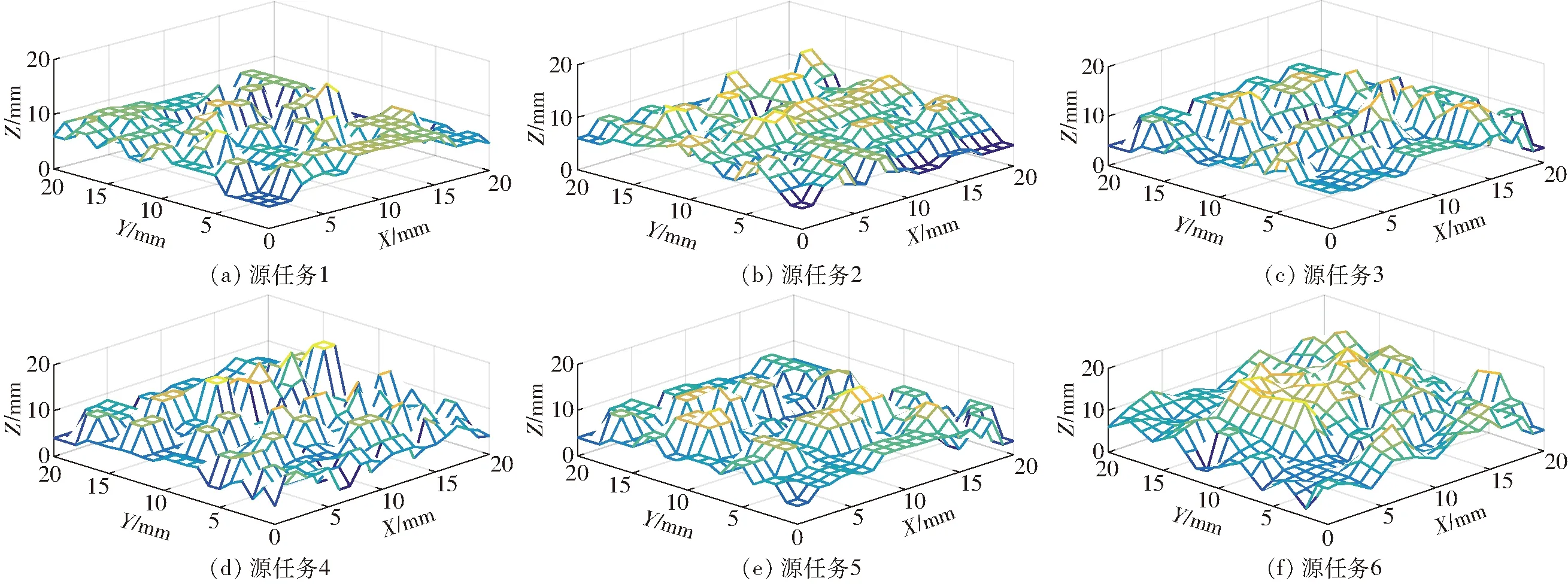
图7 机器人源任务与目标任务环境模型Fig.7 Robot source task and target task environment models

根据图6所示机器人模型所处环境和工况的不同，使用本文提出的三维环境建模方法对机器人不同作业任务时的环境进行建模，得到如图7所示的仿真地形图。图7a～7e作为源任务的环境仿真模型，图7f作为目标任务的环境仿真模型。图中栅格下方代表障碍物，X、Y方向每个单元格代表实际的机器人运动距离(15 mm)。各任务都是给定运动的起始点与终止点，使用蚁群算法寻找一条最短路径。

3.2 参数迁移与传统方法对比实验

为了验证本文所提出算法的有效性，将使用参数迁移选择蚁群参数方法与使用传统参数选择方法进行对比。使用随机试凑法和实验试凑法两种传统参数选择方法为目标任务寻找最优参数，再以参数迁移方法寻找最优参数。本仿真实验的目的是将源任务的经验知识通过处理迁移到目标任务上，给出一组最优解，使得目标任务可以快速规划出一条最短路径，并验证其方法的有效性和快速性。

不同源任务参数之间的迁移性能如表1所示，map1～map5是源任务1～5的环境模型，map6是目标任务的环境模型。

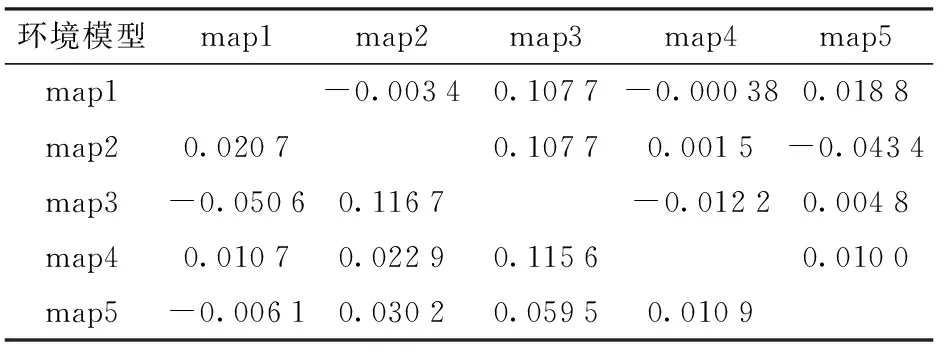
表1 源任务之间的迁移性能Tab.1 Transfer performance between source tasks

表1中行代表源任务，列代表被迁移的任务，各任务之间的迁移性能由迁移参数fi,j表示。因为蚁群算法寻优过程的随机性，取10次实验数据的平均值作为结果代入迁移公式进行计算。从表中可以看出，参数迁移的迁移性能参数不具有对称性，即fi,j≠fj,i。虽然各个源任务选取的都是经验参数，但各组经验参数也具有一定的优劣区别，如各源任务参数对任务3的迁移均为正向迁移，说明源任务3的原始经验参数略差。

表2为各源任务参数对目标任务的迁移性能。为目标任务分配一组随机参数，计算各源任务对目标任务的迁移性能。可以看出源任务3对目标任务的迁移性能最优。

表2 源任务对目标任务的迁移性能Tab.2 Transfer performance of source tasks to target tasks

方法1使用随机试凑法为目标任务蚁群算法分配一组随机参数计算路径长度；方法2为通过实验试凑法为目标任务分配一组经验参数，计算其蚁群优化后的路径长度；方法3通过参数迁移将源任务的经验参数代入，计算经过参数迁移后的蚁群路径规划长度。方法3中经过参数迁移后得到的目标任务优化参数为：α=1.302 7，β=8.423 3，ρ=0.415 2，Q=174.058 2。

因为蚁群算法具有随机性，同一组参数得到的优化结果可能也具有随机性，所以每组数据均取10次平均值作为结果，得到3种方法的优化对比曲线，如图8所示。

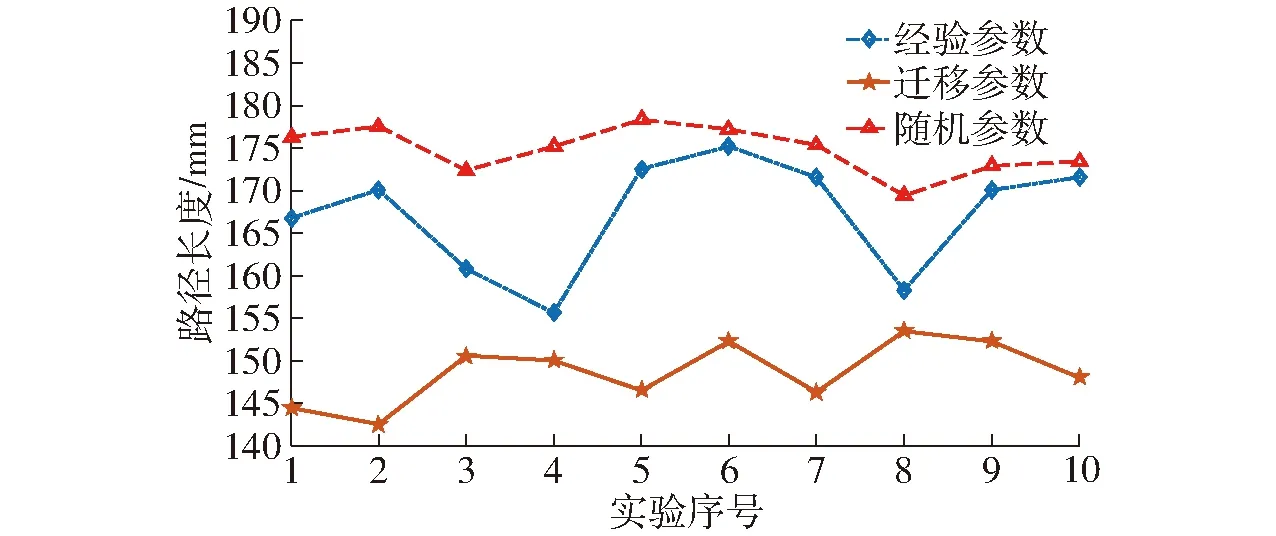
图8 性能对比Fig.8 Performance comparison diagram

从图8可以看出，使用参数迁移得到的蚁群参数进行路径规划，路径长度明显较短，平均为148.662 1 mm，经过参数迁移所寻找到的优化参数，相较于经验参数得到的机器人三维路径更优，而随机参数所得到的三维路径效果都较差。从时间上考虑，本文所提出的使用参数迁移寻找蚁群算法优化参数，用时只需120 s左右，而使用实验试凑法寻找优化参数，1 000组数据大概需要3×104s，参数迁移可以极大地提高蚁群三维路径寻优算法中选取优化参数的速度。以上实验将参数迁移方法与经验参数和随机参数进行对比，验证了将已有知识迁移到目标任务的有效性。

3.3 参数迁移与其他优化方法对比实验

为进一步验证使用参数迁移算法选择蚁群参数的有效性，本文实验还使用其他一些智能优化算法选择蚁群算法参数作为实验对比。本文选择基于遗传算法的蚁群参数选择方法和基于粒子群算法的蚁群参数选择方法作为对比。其中遗传算法中各参数设定为：染色体种群个数为100，染色体节点数为4，交叉概率Pc=0.2,变异概率PN=0.2，最大进化次数K=60。粒子群算法中各参数设定为：粒子数100，学习因子c1=c2=0.1，最大迭代次数为100。每种算法取10次实验平均值作为结果进行对比。遗传算法和粒子群算法的适应度函数为使用蚁群算法进行路径寻优的目标函数，即为蚁群算法路径规划后的路径长度。

表3为3种智能优化算法在蚁群参数优化中的性能比较，从表3可知，蚁群算法可能有多组优化效果较好的参数组，不同的参数组可能具有相近的路径规划性能。使用参数迁移、粒子群、遗传3种优化算法选择蚁群参数进行三维路径规划，结果如图9所示。

表3 3种智能优化算法在蚁群参数优化中的性能比较Tab.3 Performance comparison of three intelligent optimization algorithms for optimization of ant colony parameters

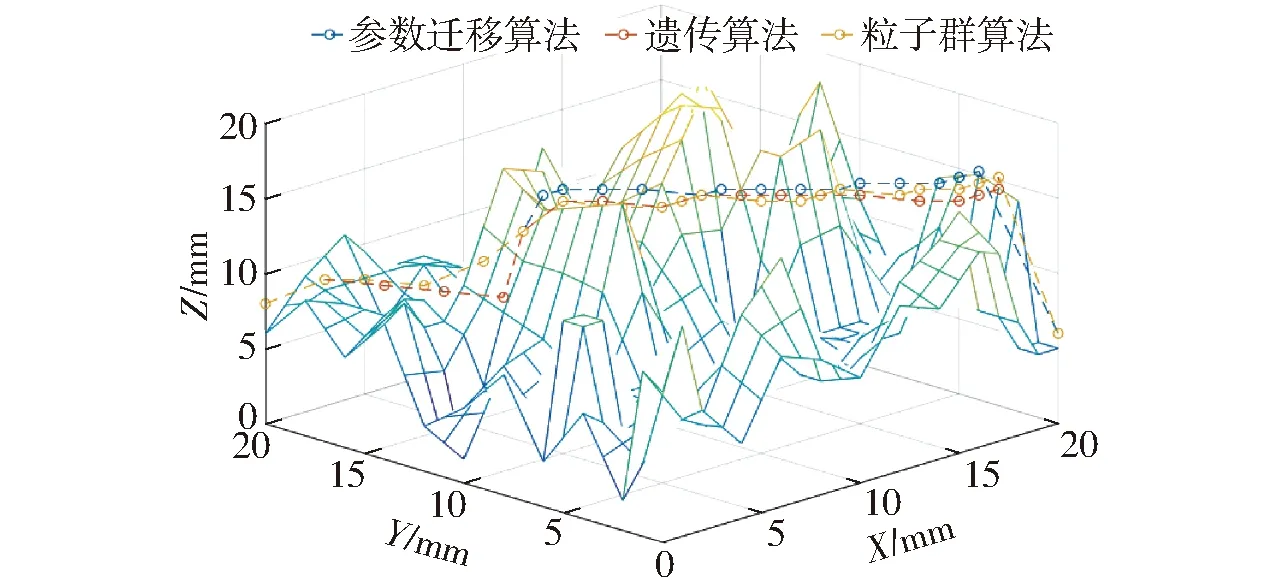
图9 3种算法的路径规划结果Fig.9 Three algorithm path planning results

从路径规划性能上看，使用参数迁移得到的优化参数在进行蚁群算法路径规划时，具有明显比遗传算法和粒子群算法选择的优化参数更优的规划效果。从时间上看，参数迁移寻找蚁群优化参数需要121.415 3 s，远远小于遗传算法的2.424 8×104s和粒子群算法的7.563 3×104s，这是因为遗传算法和粒子群算法作为一种智能优化算法，在粒子或染色体的适应度计算过程中需要反复调用蚁群算法，消耗了大量时间。

4 结束语

针对6自由度机器人末端执行器三维路径规划中蚁群算法参数设置问题进行了研究，提出了一种基于蚁群算法参数迁移的机器人三维路径规划算法。使用参数迁移算法，将源任务的经验蚁群参数知识合理迁移到目标任务，得到目标任务的蚁群优化参数组合，进而完成机器人三维路径规划任务。仿真实验表明，参数迁移显著节省了机器人蚁群算法三维路径规划任务需要的时间，路径规划所需时间从数小时减少到2 min左右，并提高了三维路径规划的性能。相较于传统参数选择法和其他智能优化算法，参数迁移可以快速得到蚁群算法的优化参数组合，这种方案可以有效解决机器人三维路径规划问题。