不同半径圆柱诱导CH4/空气预混燃烧的计算研究

余亦泽, 徐胜利, 张梦萍, 张竹鹤

(1. 中国科学技术大学 数学学院, 安徽 合肥 230026; 2. 清华大学 航空航天学院, 北京 100084)

0 引 言

为捕捉化学非平衡湍流流动(燃烧等)的精细结构，Boger等开展了直接模拟(DNS)[1-2]和大涡模拟(LES)[3-4]等计算研究。LES在亚网格尺度采用和非定常雷诺平均(URANS)湍流计算相似的模化思想，降低了计算结果对湍流模型的依赖性，即湍流模型只用于亚网格尺度。已有湍流模型主要来自不可压缩流动思想，湍流模型及其常数和工况相关，这给可压缩湍流流场计算带来不确定因素。DNS计算不需要湍流模型，但要求网格和时间尺度均小于对应的Kolmogorov尺度。和URANS相比，LES和DNS计算都采用细网格，计算量增大。

URANS高精度计算是开展LES和DNS计算的基础，URANS采用高精度数值格式可减小计算量。Balsara和Shu的LES计算结果表明[5]：要得到近似相同的计算结果，和9阶格式相比，2阶格式在各坐标轴方向的网格数约为前者4倍。当网格数相同，9阶格式计算量是2阶格式的3倍。对三维问题，要得到近似相同的计算结果，2阶格式计算量是9阶格式44/3(≈85)倍。

可压缩化学非平衡流动高精度差分计算遇到的问题是：(1)如何处理复杂几何域?(2)高精度数值格式如何满足保自由流要求?贴体变换是处理复杂几何域常用方法之一。在变换后的曲线坐标系中，如果格式不能满足自由流条件，会导致计算出现数值误差，抹平细微湍流结构或者气动声学波等微弱的物理扰动。同时，不保自由流条件产生的计算误差还会导致高阶格式数值不稳定[6-7]。

针对两类高精度中心型紧致格式，在三维广义坐标系中，Visbal和Gaitonde[7]仔细研究了Thomas和Lombard[8]提出的守恒形式网格导数差分误差，发现网格导数项和对流项采用相同差分格式，紧致格式才能保持自由流条件。但标准高阶WENO格式数值通量是直接重构分解后的通量，通量包含了网格导数。当非线性重构通量时，很难将Visbal和Gaitonde想法[7]应用到标准WENO格式，从而无法满足流表面的网格导数表面守恒(surface conservation law)和体守恒(volume conservation law)。因此，标准WENO格式在曲线网格的多维流场计算难以保持精确的自由流解[5]。JIANG等人[9]提出基于对解进行WENO插值的另一种WENO格式，随后将Visbal和Gaitonde[7]想法应用到新WENO格式[10]。针对多种不规则和运动网格以及超声速圆柱绕流，JIANG等研究新WENO格式保自由流和保涡(vortex-preserving)性质。结果表明：不论是固定网格还是动网格，相对于标准WENO 格式，新WENO格式(简称保自由流WENO格式)都可保证自由流条件和涡条件。

在本文条件下，预混燃烧主要受化学动力学机理影响。对圆柱诱导预混燃烧问题，圆柱诱导的激波和火焰驻点距离可检验不同基元反应模型的点火延迟[11-14]。采用9 组分/12步基元反应模型，Soetrisno[15]计算了CH4/空气的激波和火焰耦合流场。采用由33组分/149步基元反应模型得到的简化模型(19组分/52步反应)，Yungster和Robinowitz[11]计算了CH4/空气解耦的爆轰波流场。采用14组分/19步基元反应模型，Toshimitsu[12]较好预测了CH4/空气预混燃烧的点火延迟。冲压加速器[16]和斜爆轰发动机[17]推进原理也是基于超声速来流预混燃烧。

为开展超声速化学反应流场高精度计算，针对圆柱诱导CH4/空气超声速来流预混燃烧问题，本文在曲线坐标系应用保自由流WENO格式进行求解，研究圆柱不同半径对计算结果的影响。

1 控制方程和定解条件

1.1 曲线坐标系下的控制方程

本文计算采用Euler方程形式为:

(1)

其中，坐标变换取t=τ，x=x(ξ,η,ζ)，y=y(ξ,η,ζ)，z=z(ξ,η,ζ)。

Q=J-1Q，Q=[ρ1,…,ρns,ρu,ρv,ρw,E]T，

E(Q)=[ρ1u,…,ρnsu,ρu2+p,ρuv,ρuw,u(E+p)]T，

F(Q)=[ρ1v,…,ρnsv,ρuv,ρv2+p,ρvw,v(E+p)]T，

G(Q)=[ρ1v,…,ρnsv,ρuw,ρvw,ρw2+p,w(E+p)]T，

(2)

其中，Ru是普适气体常数，T是混合物温度，Wi是第i组元摩尔质量。

1.2 热力学参数

对ns组元量热完全气体构成的混合物，第i组元定压比热cpi和hi由多项式拟合得到，即:

(3)

(4)

其中，a1i,a2i,…,a6i取自JANAF表[18]。

1.3 基元反应模型

包含ns组元、NR反应步的基元反应统一表示为:

(5)

由质量作用定律得到第i组元的质量生成速率为:

(6)

其中，kf和kb分别为正向和逆向反应速率常数，通常为Arrhenius定律形式，具体为:

(7)

其中，Aj、βj、Eaj分别为第j步反应的指前因子、温度指数和活化能。平衡常数Kcj由Gibbs自由焓确定[19]，逆反应速率常数kbj由kfi和Kcj确定，即:

(8)

本文采用的基元反应模型[9]见表1所列。

2 数值方法简介

2.1 保自由流WENO格式

采用保自由流5阶WENO格式求解方程(1)，方程(1)半离散格式为:

(9)

表1 CH4/空气基元反应模型Table 1 Chemistry model for methane air mixture

保自由流WENO和标准WENO格式的差异在于数值通量重构方法不同，前者数值通量由解和解的导数插值后得到[10]。以ξ方向为例，有

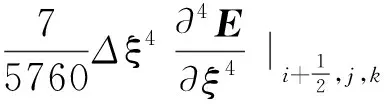
(10)

2.2 三阶TVD Runge-Kutta方法

采用三阶TVD Runge-Kutta方法离散方程(1)时间导数项。对:

(11)

具体形式为[20]:

(12)

其中，Δt为时间步长，Lh为空间离散算子。

3 计算结果分析和讨论

3.1 数值方法验证

从格式精度和保自由流性质两方面验证本文选用的数值方法。参考文献[9]，取如下变换:

x=ξ+0.01sinξcosη

y=η-0.02cosξsinη

对方程(1)，初值取为:

ρ=1.0+0.2sin(x+2y)

p=1.0,u=0.5,v=-0.5

在(x，y)采用以2π为周期的周期性边界条件。表2给出t=2密度计算值的L1和L∞误差以及对应的阶。从表2看出，本文采用的WENO格式具有5阶精度。

表2 ρ的L1和L∞误差以及对应的阶(t=2)Table 2 L1 errors and L∞ errors and related order of ρ at t=2

本文选用Jiang[9]的算例验证新WENO格式保自由流条件。取如下计算网格:

xi,j,k=-2+(i-1)Δx0+

0.2sin [π(j-1)Δy0]sin[π(j-1)Δy0]

yi,j,k=-2+(j-1)Δy0+

0.2sin[π(k-1)Δz0]sin[π(i-1)Δx0]

zi,j,k=-2+(k-1)Δx0+

0.2sin[π(i-1)Δx0]sin[π(j-1)Δy0]

其中，i=1,2,…,Imax，j=1,2,…,Jmax，k=1,2,…,Kmax，Imax=Jmax=Kmax=21，Δx0=Δy0=Δz0=0.2，Δt取为0.05，最大计算时间取为10，ρ和声速设为常数，自由流沿x方向且马赫数为0.5。表3给出了标准WENO和保自由流WENO格式计算得到v和w的L2误差。表3表明：保自由流WENO格式的L2误差接近机器误差，标准WENO的L2误差约为10-3，这验证了保自由流WENO的保自由流性质，也校验了本文计算程序。要说明的是：保自由流WENO格式更多精度分析和算例验证见文献[9, 10]。

表3 v和w的L2误差Table 3 L2 errors of v and w

3.2 圆柱诱导CH4/空气超声速预混燃烧

本文选择和非平衡化学反应流计算的的标模算例结果[11]进行对照。算例1给出圆柱诱导超声速预混燃烧示意图(图1(a))，圆柱半径R为0.5 mm，圆心位于x=-1。计算参数和边界条件简述如下：

自左至右来流静温T∞、静压p∞和速度U∞分别为295 K、51 kPa和2330 m/s，对应的马赫数Ma∞为6.61，预混气为化学计量比CH4/空气混合物，计算网格取40×30，见图1(b)。入口边界AD指定超声速来流参数，出口边界AB和CD取外推条件，固壁BC采用绝热滑移条件。

图1 圆柱诱导超声速预混燃烧和计算网格示意图Fig.1 Schematic of a cylinder induced combustion and grid distribution

图2和图3分别给出压力和温度等值线与云图分布。图2清楚地显示圆柱上游产生的弓形激波位置。图3也显示了激波和火焰阵面位置，对应着两道温度间断。自左至右的第一个温度间断是弓形激波产生的波后气流温度上升，第二个温度间断对应化学反应(燃烧)放热导致的温度上升。图2和图3均表明：激波和火焰阵面的厚度很薄，特别是火焰阵面，这表明预混燃烧的化学反应速率很大。仔细观察还可看出，沿着图3火焰阵面远离对称线，火焰厚度随着距离增大而略有增大，相当于火焰厚度略微变厚。原因是：弓形激波后的当地气流Ma数逐渐变大且温度降低。根据方程(7)和(8)，当地燃烧kfj和kbj略有减小，化学反应速率略有降低，从而导致预混火焰阵面略微变厚。

图2 压力分布等值线和云图(算例1)Fig.2 Pressure contours and snapshots (case1)

图3 温度分布等值线和云图(算例1)Fig.3 Temperature contours and snapshots (case1)

图4给出压力和温度沿过驻点水平线的分布。图4(a)显示压力只有一次上升，这表明火焰面两侧压力近似相等，近似为等压燃烧。图4(b)显示了温度两次上升，这和图3也是对应的。为了定量考察计算结果的网格无关性，图4还给出了网格加密一倍(80×60)后的压力和温度计算结果。图4表明：当计算网格加密一倍(80×60)，粗细网格计算得到的压力和温度沿驻点线分布近似重合。这表明本文粗网格计算得到的计算结果也是可靠的。图4(c)还给出典型反应物(CH4、O2)和生成物(H2O、CO2)质量百分数沿过驻点线分布。图4(c)表明：化学反应区约占据9 网格点。显然，本文采用网格量是可以分辨化学反应区的。图5给出了Yungster[11](网格数91×91)和本文计算得到的激波和火焰阵面位置。这些数据分别从Yungster[11]温度等值线和本文图3提取的。图5表明：尽管本文计算采用网格数较少(40×30)，但是，两者的激波形状近似重合，火焰面位置也大致重合，只是在远离过驻点线的重合度略差，可能原因是本文和Yungster采用不同基元反应模型。

在达到同样收敛解前提下，采用5阶WENO格式、较少网格数(40×30)和2阶TVD格式、较多网格数(91×91)，所用CPU运算时间分别约为6 h和10 h，这表明：在本文条件下，采用高精度格式和较少网格数可提高计算效率。

(a) 压力

(b) 温度

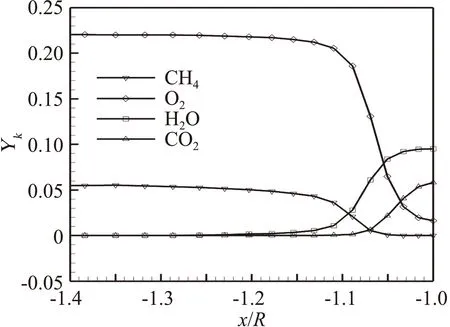
(c) 组元质量百分数

图5 本文和Yungster[11]激波和火焰面位置(算例1)Fig.5 Shapes of a shock and a flame front in contrast to those in Ref[11](case 1)

3.3 不同圆柱半径的影响

以算例1为参考，本节研究不同半径圆柱诱导CH4/空气超声速预混燃烧的影响。来流参数和边界条件同算例1，图6给出了R分别为1.5 mm和3.5 mm对应的温度等值线与云图分布。

图6表明：和图3类似，不同半径圆柱上游流场均产生两道温度间断，分别对应弓形激波(自左至右第一个间断)和火焰面(自左至右第二个间断)的气流温度上升。R分别为1.5 mm和3.5 mm的圆柱，对应的激波驻点距离分别为0.18mm、0.59mm和1.82mm，驻点距离随着圆柱半径增大而增大。即使不考虑来流预混气的化学反应，不同半径圆柱对上游来流的阻碍作用不同，所产生的弓形激波形状或强度也不相同，即弓形激波后的气流温度不相同。根据方程(7、8)，不同温度对应不同的kfj和kbj，从而影响当地化学反应速率，造成预混燃烧流场温度和压力也不相同。

R分别为0.5 mm、1.5 mm和3.5 mm圆柱，对应的火焰面驻点距离分别为0.05 mm、0.51 mm和1.75 mm。和激波驻点距离类似，火焰面驻点距离随圆柱半径增大而增大。

(a) R=1.5 mm(算例2)

(b) R=3.5 mm(算例3)

从图6还可看出，弓形火焰面(化学反应区)几何形状和激波形状类似。尽管来流条件相同，但是，不同半径圆柱对应的激波和火焰面之间距离是不同的，两者沿驻点线的距离是最小的。原因是：来流经过弓形激波压缩，弓形激波波后气流沿激波阵面法线的Ma数是不同的，偏离驻点线越远，沿激波阵面法线Ma数就越小。根据激波关系，对应的气流温度和压力也就越低。由基元反应质量作用定律知，组元密度时间变化率和温度、分压力(对应摩尔浓度)是直接相关的。因此，弓形激波阵面不同位置对应的预混气流反应速率也是不同的。沿激波阵面离开驻点线，弓形激波后气流化学反应由当地亚声速转变为超声速。不同的波后气流压力和温度对应着不同的反应速率，宏观上表现为图6弓形激波和弓形火焰面之间的不同距离，该距离通常称为点火延时距离(ignition induction length)。和当地气流速度关联，由点火延时距离可得到点火延时(ignition delay)。测量过驻点线的圆柱上游激波和火焰之间距离，换算为基元反应动力学机理对应的点火延时，表4给出本文不同半径圆柱对应的点火延时计算值。为和实验数据对比，根据激波管甲烷点火延时数据整理的拟合公式[22]:

(16)

其中：τ为点火延时，μs；T为温度，K；[O2]和[CH4]分别为O2和CH4摩尔浓度，mol/cm3。从表4看出，拟合公式[22]给出的点火延时和本文计算值较接近。点火延时随圆柱半径增大而增大。

表4 不同半径圆柱对应的点火延时计算值和拟合值Table 4 Computed and fitted ignition delay at different cylindrical radiuses

对应图2、图3和图6，图7给出压强和温度沿过驻点线分布。作为比较，图7还给出R为0.5 mm圆柱无化学反应流场激波驻点距离。为清楚地显示不同算例结果的差别，图7只显示圆柱表面左侧附近的区域。图7(a)表明：不同半径圆柱对应的激波驻点位置是不同的，圆柱半径越大，对应的驻点距离也越大。图7(b)表明：来流经过弓形激波和火焰面到达圆柱表面，不同半径圆柱对应不同的火焰面位置，但燃烧产物在圆柱表面的最大温度相同，这表明圆柱上游的预混气燃烧是充分的。对R为3.5 mm圆柱，激波和火焰面沿过驻点线的距离最短。这表明：圆柱半径越大，对预混燃烧流场的影响也越大。原因是：弓形激波下游气流是局部亚声速流动，圆柱对流场扰动(阻挡作用)向上游传播，从而影响激波和火焰驻点距离。这和图6与图7(a)给出的结论也是一致的。

(a) 压强

(b) 温度

图8给出流场Ma数云图分布。图8表明：弓形激波和火焰面下游气流Ma数低于来流。经过激波后，超声速气流速度降低，但温度和压力升高，气流动能转变为内能，有利于可燃预混气燃烧。图8还给出过驻点线两侧附近的亚声速流场分布，不同半径圆柱对应的亚声速区域大小也不相同。其中，R=0.5 mm圆柱对应的亚声速区域最小，R=3.5 mm圆柱对应的亚声速区域最大。在弓形激波波后流场，Mach数随着离开驻点线距离增大而逐渐增大，即由亚声速区过渡到超声速区，分别对应着亚声速燃烧和超声速燃烧。图8还可解释不同半径圆柱在驻点线附近流场存在的壁面、火焰面和激波之间相互干扰。圆柱壁面对来流扰动通过亚声速区域向上游传播，直至影响到激波和火焰阵面。

对R为1.5 mm和3.5 mm圆柱预混燃烧流场，图9给出本文和Yungster[11]计算得到的激波和火焰面位置。和图5类似，图9的激波和火焰位置数据也是从温度等值线提取的。图9表明：当R=1.5 mm，Yungster[11]与本文得到的激波和火焰面位置基本重合，只是远离过驻点线的火焰面位置略有差异。当R=3.5 mm，Yungster和本文计算得到的激波位置大致重合，但在远离驻点线的区域，激波和火焰面位置存在差异，其中，火焰面位置的差异尤其明显。主要原因是Yungster采用了不同的基元反应模型和网格分布。两者在过驻点线附近区域的激波和火焰面位置完全重合。本文和Yungster得到的弓形激波无量纲驻点距离均为xshock/d=0.3。其中，xshock和d分别是激波驻点距离和圆柱直径。这和文献[21]激光全息得到xshock/d=0.29值非常接近。

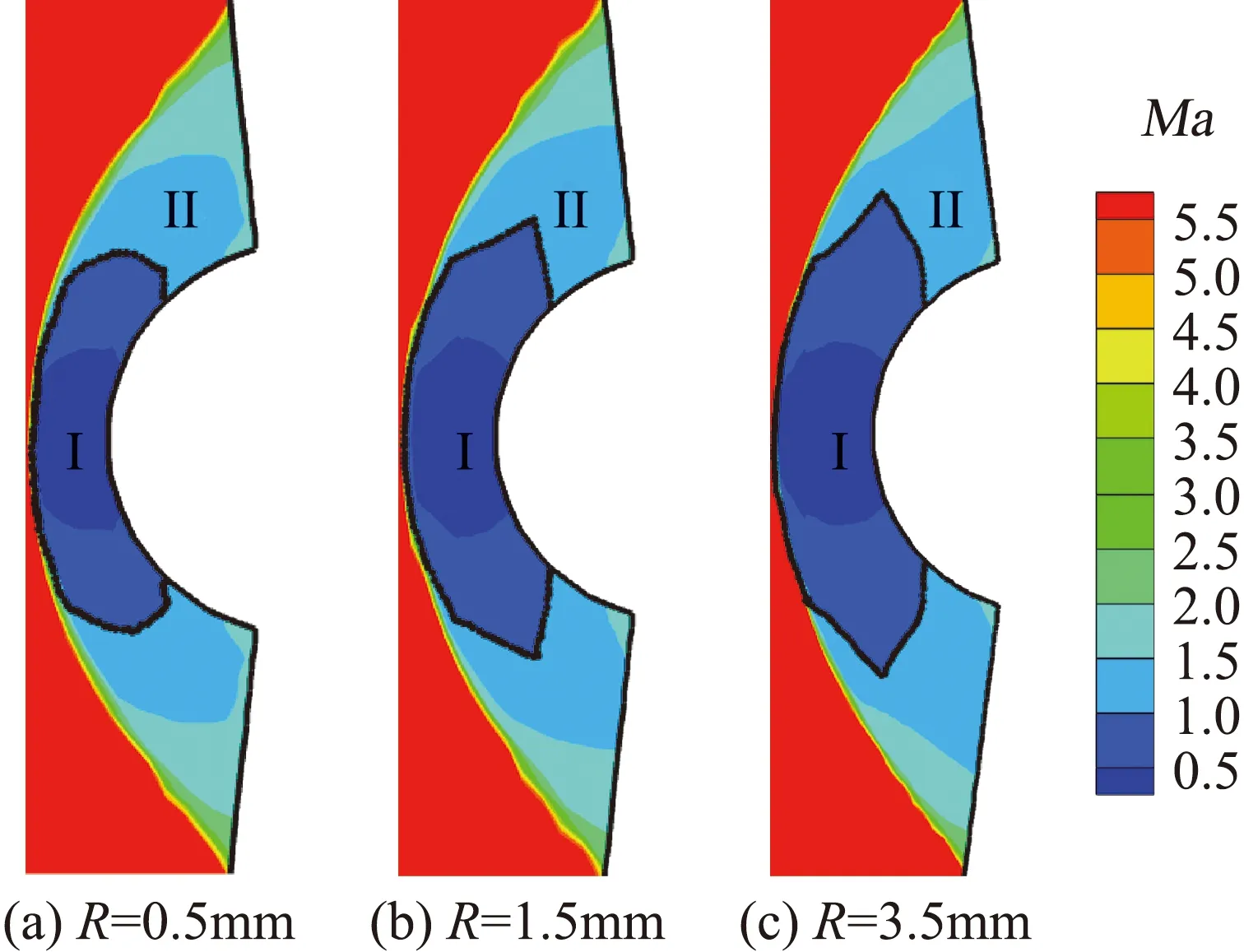
图8 马赫数分布云图Fig.8 Mach number counter map

(a)R=1.5 mm

(b)R=3.5 mm

图9 本文和Yungster[11]激波和火焰面位置
(算例2和算例3)
Fig.9 Shapes of a shock and a flame front in contrast
to those in Ref[11](case2 and case3)

4 结 论

1) 在本文条件下，采用保自由流5阶WENO格式计算圆柱诱导CH4/空气预混燃烧流场，消除了曲线网格下不保自由流产生的计算误差，表现了较好计算稳定性，这和文献[9]结论是相同的。

2) 本文得到的激波和火焰面形状与文献计算结果相符，特别是过驻点线的激波和火焰位置完全相同。和文献[11]二阶TVD格式相比，采用保自由流5阶WENO格式和近似四分之一网格数，得到近似相同的计算结果，提高了计算效率。

3) 圆柱不同半径影响着超声速来流预混燃烧的激波和火焰面驻点距离。圆柱半径越大，对应的火焰面和激波之间距离也越小，相应的点火延时也越小。圆柱表面对来流阻碍作用或扰动，通过圆柱上游的亚声速区传播，改变着过驻点线附近的弓形激波和火焰面形状和驻点距离。