考虑绳阻尼的绳系并联机器人动力学特性分析
彭苗娇,吴惠松,林麒,周凡桂,柳汀,王晓光
(厦门大学 航空航天学院,厦门361005)
绳索具有线密度低、强度高、柔性好等特点,因此广泛应用于各种工程领域,包括斜拉桥[1]、船舶起重[2]、绳系卫星[3]、大型射电望远镜[4]、风洞试验[5-7]等。绳索的阻尼特性是影响机构功能的重要因素之一,也是设计中需要考虑的重要参数。绳索的材料、长度、直径、预紧力不同,都会导致绳索阻尼有较大差异,而目前尚缺乏可靠、完整的绳索阻尼数据库可供查询。
阻尼的理论计算方法有复数特征值法、模态应变能法、有限单元法和Rayleigh-Ritz法等[8-12],但是这些方法基于线性黏弹性振动理论,即假定振动过程中张力、几何形状等不变,忽略了阻尼的非线性特性,且计算方法复杂,无法高效准确地对阻尼进行评价。现有文献对绳阻尼的研究均针对粗绳(直径>2mm)[13-16],由于阻尼的非线性,文献[17-19]中提到的针对粗绳阻尼的理论计算方法不一定能适用于细绳(直径≤2mm),因此本文采用实验方法研究细绳的阻尼特性。
目前,绳系并联机构具有工作空间大、负载能力强、刚度高等特点,已成为国内外的研究热点[4-7]。特别在风洞试验领域,绳系并联机构作为一种新型支撑方式,与传统的硬式支撑相比,具有刚度大、对流场干扰小、易实现高速及复杂规律的运动等优点[20],近年来引起国内外学者广泛关注。然而,在现有文献中,大部分未考虑绳阻尼的影响,个别虽考虑了绳阻尼,但绳阻尼系数是虚构值。汪选要等[21-22]将柔索简化成刚度为常值的弹簧,建立了并联柔索机构的动力学模型,进行了轨迹跟踪控制的研究,但没有考虑绳阻尼的影响。刘欣等[23]考虑了绳的弹性变形,进行了绳牵引并联机器人的运动控制研究,但没有考虑绳阻尼的影响。文献[24]的研究表明,绳阻尼对末端执行器的位姿具有显著的影响,但绳阻尼系数是虚构值。文献[25]考虑绳索弹性、阻尼和拉伸效应,给出了绳牵引并联支撑系统的振动特性,但绳阻尼比是虚构值。高估或低估绳索阻尼,将给绳系并联机构的设计带来较大误差,甚至影响机构整体的安全性。因此,研究绳索的阻尼特性,并分析绳阻尼对绳系并联机构的动力学特性的影响具有重要意义。
不失一般性,本文以应用于风洞试验新型支撑的绳系并联机器人(W ire-driven Parallel Robot,WDPR)为例,研究绳阻尼对WDPR在风洞试验中的动力学特性的影响。本文提出了测量绳阻尼的实验方法,解决了细绳阻尼的测量困难;通过采用绳阻尼比的实验测量值,建立WDPR的有阻尼动力学方程,分析风洞来流冲击作用下WDPR的动力学响应,给出了绳阻尼对WDPR动力学特性的影响判据。
1 绳阻尼特性测试
阻尼比的定义是阻尼系数与临界阻尼系数之比[26],用于表达结构体标准化的阻尼大小。根据阻尼的产生机制[27],本文研究绳的内部阻尼,即来自于材料内部各种微观和宏观过程的机械能耗散,以下简称阻尼。
1.1 实验原理
目前,对绳阻尼的测量一般采用激光位移计或应变片测量的方式[15,18-19],而这2种方法均不适用于细绳(直径≤2mm)的阻尼测量。因为绳太细,激光位移计的测量变得十分困难甚至不可用;粘贴应变片,则会改变细绳的动特性,影响阻尼测量结果的准确性。本文采用高速相机测量的方式,属于非接触式的测量方式,由于无需在绳索上附加任何质量元件,绳索本身的特性不被改变,特别适用于细绳(直径≤2mm)阻尼的测量,同时也适用于粗绳(直径>2mm)。
实验原理如图1(a)所示。实验时先将绳索张紧,在绳索中央悬挂重物施以载荷;待重物稳定后突然释放重物,即对绳索中央施加瞬间激励,使其做自由衰减振动;采用高速相机拍摄绳索中央部位的振动过程;从所拍绳索振动视频中提取绳索振幅最大处的位移信息进行数据处理和分析,得出与绳索阻尼特性相关的参数。通过该实验装置可测量不同长度、直径、预紧力和材料的绳索的阻尼参数。
绳阻尼实验装置的实物图如图1(b)所示。实验台架采用欧标6060L双槽工业铝型材搭建,以保证实验台架具有良好的强度、刚度和稳定性;并以水平仪校核其水平度和垂直度。采用型号为CHC-S的拉力传感器(量程为200 N,精度为0.1%)测量绳张力。采用高速相机(型号:FASTCAM Mini AX200)获取绳索振动位移。标定板用于在数据后处理中确定绳索在振动中的实际位移。

图1 绳阻尼实验原理及装置Fig.1 W ire damping experimental principle and device

图2 实验绳样本Fig.2 Wire samples for experiment
如图2所示,选择3种不同直径的Kevlar绳作为实验样本,其物性参数如表1所示。通过设置不同的绳索参数(直径d、预紧力作用下的初始绳长L0和预紧力T0)进行实验,得到不同绳索参数下的阻尼比。

表1 绳样本的物性参数Table 1 Physical param eters of w ire sam p les
1.2 数据处理方法
采用对数衰减法进行数据后处理。记绳中点振动位移响应为dy。图3为实验数据dy随时间衰减的曲线。
如图3所示,Ai代表绳振动衰减曲线dy的一个峰值,Ai+r代表第r个周期后的峰值,可得[27]
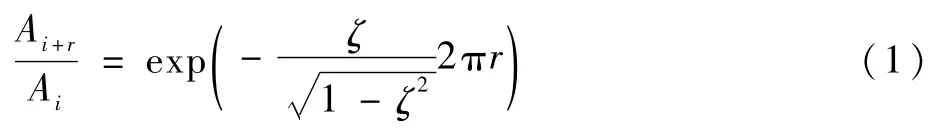
则对数衰减率δ为
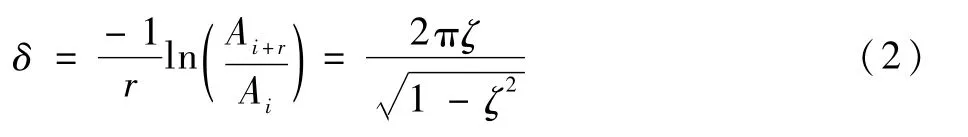
由式(2)可得绳阻尼比ζ的表达式为

通过实验测得绳索的振动位移响应曲线,利用式(2)和式(3)进行数据处理,即可得到绳阻尼比。

图3 绳在竖直面内的振动位移响应(d=0.6mm,L0=1m,T0=30N)Fig.3 Vibration displacement response of wire in vertical plane(d=0.6mm,L0=1m,T0=30N)
1.3 实验结果
不同直径、不同初始绳长的Kevlar绳在不同预紧力作用下的阻尼实验结果如图4~图6所示。
从图4可见,绳阻尼比随预紧力的增加而减小。T0∈[20,80]N时,绳阻尼比的下降速率很快;T0∈[90,145]N时,绳阻尼比的下降速率趋于平缓,且绳阻尼比随预紧力的变化呈现非线性。

图4 绳阻尼比与预紧力的关系(d=0.6mm,L0=1m)Fig.4 Relationship between wire damping ratio and preload(d=0.6mm,L0=1m)

图5 绳阻尼比与初始绳长的关系(d=0.6mm)Fig.5 Relationship between wire damping ratio and wire length(d=0.6mm)

图6 绳阻尼比与绳直径的关系(L0=1m)Fig.6 Relationship between wire damping ratio and wire diameter(L0=1m)
图5表明,绳阻尼比随初始绳长的增加而增大,但曲线变化较为平坦。在不同预紧力作用下,绳阻尼比随初始绳长的变化速率基本相同。预紧力为80 N时,绳阻尼比的分散度更小。
从图6可见,绳阻尼比随绳直径的增加而增大。当预紧力为30 N时,随着绳直径的增加,绳阻尼比明显增大;但当预紧力为80 N时,随着绳直径的增加,绳阻尼比的增大很不明显。因此,预紧力越小,绳阻尼比随绳直径的变化将不能忽略。
2 动力学建模
2.1 WDPR动力学建模
图7(a)为八绳牵引的六自由度WDPR原理样机示意图[28]。WDPR原理样机采用8根Kevlar绳做牵引绳,将飞机模型悬挂在空中;改变牵引绳的长度可对模型六自由度的运动进行控制。所建造的WDPR原理样机如图7(b)所示。
如图8所示,以静坐标系OXYZ为参考系,飞机模型的位姿记为X=[XP,YP,ZP,φ,θ,ψ]T,(XP,YP,ZP)为沿3个坐标轴的平动,(φ,θ,ψ)为绕3个坐标轴的转动。
在静坐标系OXYZ下,第i根绳的绳长矢量定义为


图7 WDPR原理样机Fig.7 WDPR prototype

图8 WDPR运动学示意图Fig.8 Kinematic schematic diagram ofWDPR

记Li为第i根绳的实时绳长,则有

根据Newton-Euler法,飞机模型的动力学方程如下:
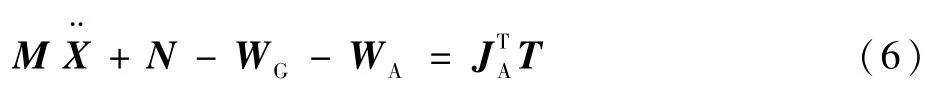
在风洞试验中,作用在飞机模型上的气动力和力矩有升力、阻力、横向力、俯仰力矩、偏航力矩和滚转力矩,其表达式如下[29]:


2.2 绳张力建模
考虑绳阻尼,采用弹簧模型对绳索进行建模,得到绳张力的表达式如下:

式中:T为绳张力;ku为未变形绳的刚度;c为绳阻尼系数;L为实时绳长;Lu为未变形的绳长。
根据绳阻尼系数和绳阻尼比的定义有

式中:ζ为绳阻尼比,其数值可通过第1节的实验测得;ms为绳单位长度质量。

式中:E为绳弹性模量;A为绳未变形时的横截面积;ρw为绳的体密度。
再根据应变公式有

联立式(9)~式(12),可得绳阻尼系数为


所以,绳张力矢量表达式为
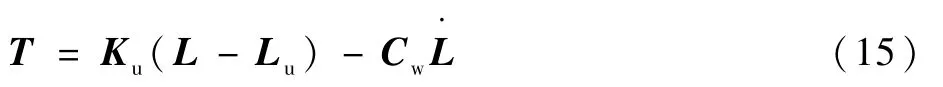
式中:Ku=diag(ku1,ku2,…,ku8);Cw=diag(c1,c2,…,c8);L=[L1,L2,…,L8]T;Lu=[Lu1,Lu2,…,Lu8]T。
2.3 WDPR的有阻尼动力学方程
联立式(6)、式(14)和式(15),可得WDPR的有阻尼动力学方程为


3 绳阻尼对WDPR动力学特性的影响
本节基于式(16)给出的WDPR的有阻尼动力学方程,研究风洞来流作用下,WDPR的动力学响应受绳阻尼的影响。
3.1 仿真条件
仿真中所用的绳参数及飞机模型参数如下:
1)绳参数。如表1所示,采用3种不同直径的Kevlar绳做牵引绳,为了便于比较,弹性模量统一取E=21.9GPa。
2)飞机模型采用SDM 标模,模型质量m=1.093 kg,机翼参考面积S=0.026 594m2,平均气动弦长cA=0.092 m,模型关于质心的惯量矩阵为

3)来流条件。以纵向测力试验[29](模型侧滑角为0°,在一系列攻角下进行测量)为例,来流速度V=17m/s,空气密度ρ=1.29 kg/m3,飞机模型攻角12°,升力系数CL、阻力系数CD、俯仰力矩系数Cm见参考文献[28]。
为了克服非线性动力学方程的求解困难,本文采用隐式的变阶Runge-Kutta数值积分方法,对式(16)进行求解。
3.2 结果与分析
通过仿真分析,得到WDPR的动力学响应曲线,如图9~图12所示。其中,飞机模型的位姿响应以飞机模型沿OX方向的位姿变化和俯仰角变化为例。
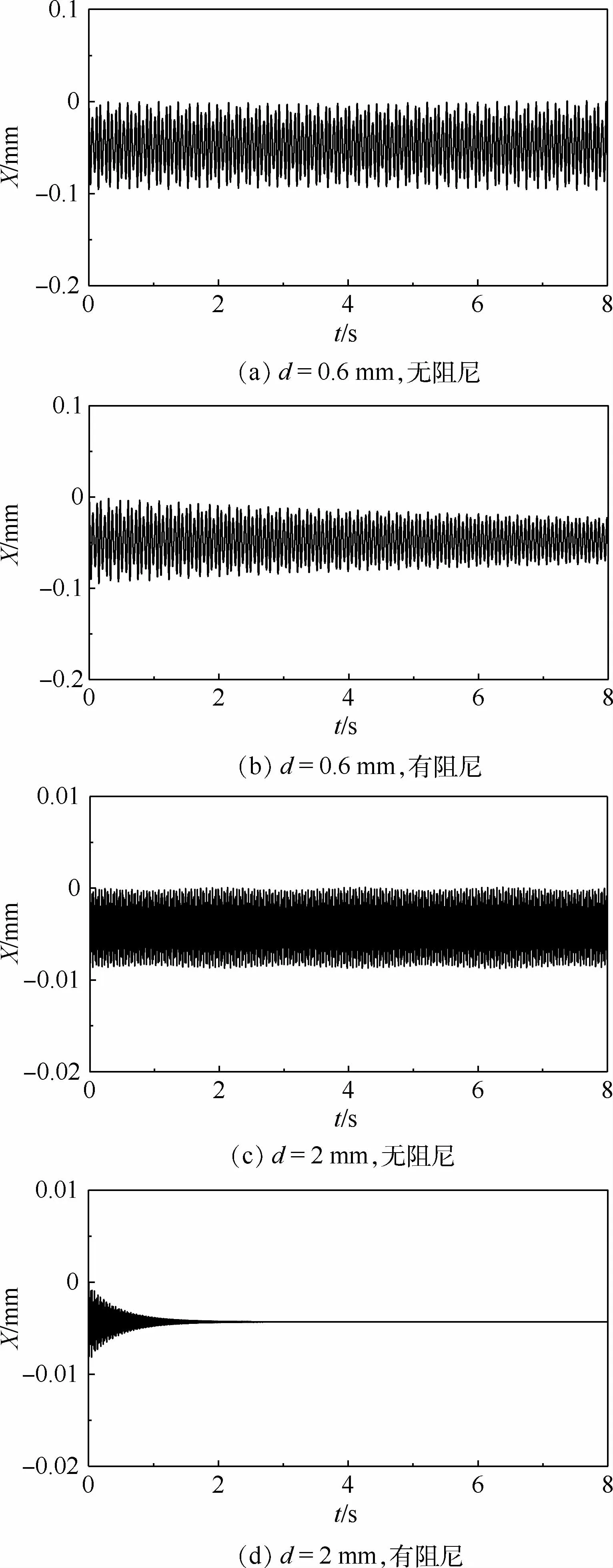
图9 飞机模型沿OX方向位姿变化Fig.9 Attitude variation of aircraftmodel along OX direction
如图9所示,当绳直径为0.6mm时,不考虑阻尼的情况下,飞机模型沿OX方向的位姿变化的峰-峰值为0.1mm;考虑阻尼的情况下,飞机模型沿OX方向的位姿变化的初始峰-峰值也为0.1mm,且随时间缓慢变小,但变化幅度不大。当绳直径为2mm时,不考虑阻尼的情况下,飞机模型沿 OX 方向的位姿变化的峰-峰值仅为0.01mm;考虑阻尼的情况下,飞机模型沿OX方向的位姿变化的初始峰-峰值也为0.01mm,且随时间快速变小,在t=3 s后趋于稳定。
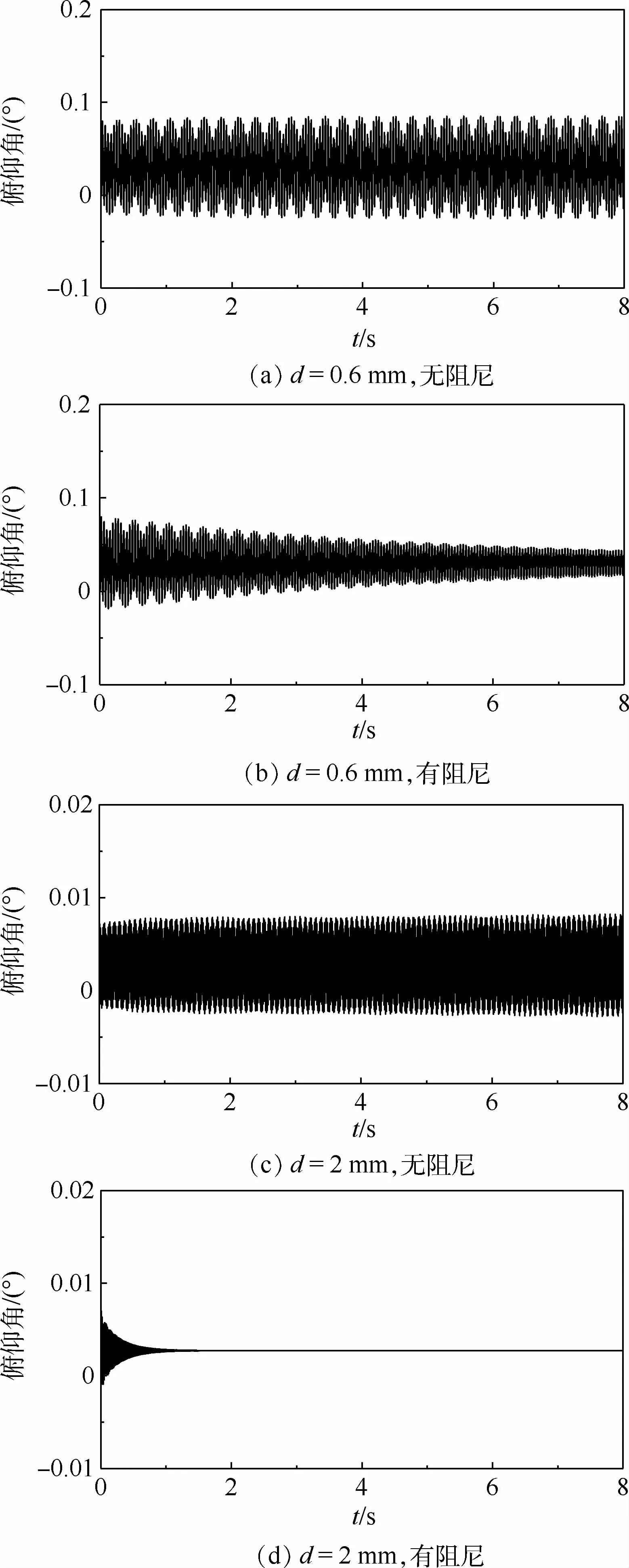
图10 飞机模型俯仰角变化Fig.10 Pitching angle variation of aircraftmodel
如图10所示,当绳直径为0.6mm时,不考虑阻尼的情况下,飞机模型俯仰角变化的峰-峰值为0.1°;考虑阻尼的情况下,飞机模型俯仰角变化的初始峰-峰值也为0.1°,且随时间缓慢变小,但变化幅度不大。当绳直径为2mm时,不考虑阻尼的情况下,飞机模型俯仰角变化的峰-峰值仅为0.01°;考虑阻尼的情况下,飞机模型俯仰角变化的初始峰-峰值为0.006°,且随时间快速变小,在t=2 s后趋于稳定。
在来流作用下,飞机模型位姿变化的同时,绳张力也随之变化。令ΔT=T-T0,ΔT为绳张力的变化量,T为飞机模型位姿变化过程中的实时绳张力。以绳5为例,如图11所示,对于不同粗细的绳,不考虑阻尼的情况下,绳张力变化的峰-峰值为2N;考虑阻尼的情况下,绳张力变化的初始峰-峰值也为2 N。在考虑阻尼的情况下,直径为0.6mm的绳的绳张力随时间缓慢变小;而直径为2mm的绳的绳张力随时间快速变小,在t=2 s后趋于稳定。

图11 绳张力变化Fig.11 W ire tension variation
综上所述,在来流作用下,采用直径较大的绳,飞机模型位姿变化和绳张力变化在短时间内能趋于稳定。因此,在绳对流场的影响可以接受的情况下,采用直径较大的绳,WDPR的稳定性更好。
图12为飞机模型位姿响应和绳张力响应曲线的局部放大图。从图12可见,无阻尼情况下,飞机模型的位姿和绳张力呈周期性振荡;考虑阻尼的情况下,飞机模型的位姿和绳张力呈衰减振荡,且绳直径较大时,振荡衰减得越快。说明绳阻尼对WDPR的动力学响应具有减振作用,且绳直径越大,绳阻尼的减振作用越明显。特别地,对于直径小于2mm的细绳来说,相比无阻尼的情况,绳阻尼对飞机模型位姿及绳张力的振荡频率和相位的影响很小,基本可以忽略。

图12 WDPR动力学响应Fig.12 Dynamic response ofWDPR
3.3 绳阻尼的影响判据
根据上述分析,直径不同的绳,对WDPR动力学响应的影响明显不同。以绳5为例,根据式(13),不同直径绳的阻尼系数如表2所示。由于阻尼比和绳直径不同,导致阻尼系数有很大差别,从而导致WDPR 的动力学响应明显不同。

表2 不同直径绳的阻尼系数(绳5)Table 2 Dam ping coefficient of w ire w ith different diam eters(W ire No.5)
直径不同的绳,其阻尼比不同,并且初始绳长、初始绳张力的不同,都会影响绳的阻尼系数。因此,以绳阻尼系数作为因变量,取2种不同直径的绳,分析其阻尼系数的变化对WDPR动力学响应的影响。定义当量系数ηX、ηP、ηT,对飞机模型位姿和绳张力进行无量纲化处理:

式中:pX0为无阻尼时飞机模型沿OX方向位姿变化的峰-峰值;pXc为有阻尼时飞机模型沿OX方向位姿变化5 s后的峰-峰值;pP0为无阻尼时飞机模型俯仰角变化的峰-峰值;pPc为有阻尼时飞机模型俯仰角变化5 s后的峰-峰值;pT0为无阻尼时绳张力变化的峰-峰值;pTc为有阻尼时绳张力变化5 s后的峰-峰值。
如图13所示,当绳阻尼系数c>0.6 N·s/m时,无阻尼与有阻尼的动力学响应峰-峰值之比将超过10,即绳阻尼的减振作用变得很显著,特别是直径粗的绳比直径细的绳,其阻尼的作用更明显。因此,在WDPR的设计中,可根据式(13)和实测的绳阻尼比计算得到,当绳阻尼系数c满足以下条件:c>0.6 N·s/m时,不论绳直径粗细如何,其阻尼对WDPR 动力学特性的影响不能忽略。
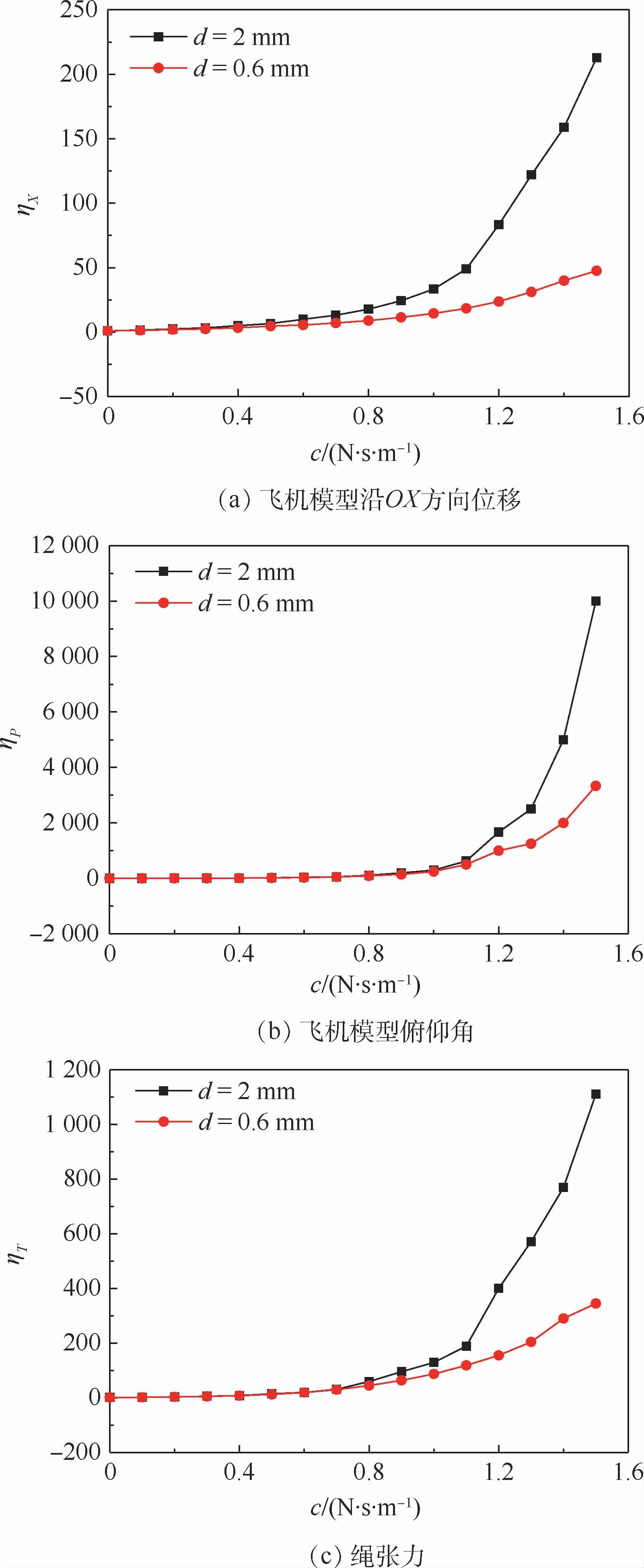
图13 绳阻尼系数变化对WDPR动力学响应的影响Fig.13 Influence of wire damping coefficient variation on dynamic response of WDPR
4 结 论
本文以应用于风洞试验模型支撑的绳系并联机器人WDPR为例,研究绳阻尼对WDPR动力学特性的影响,得出以下结论:
1)考虑绳阻尼的情况下,当绳直径较小(d<1mm)时,飞机模型位姿变化和绳张力变化的峰-峰值随时间缓慢变小,但变化幅度不大;当绳直径较大(d≥2mm)时,飞机模型位姿变化和绳张力变化的峰-峰值随时间快速变小,并在3 s后趋于稳定。因此,在绳对流场的影响可以接受的情况下,采用直径较大的绳,WDPR的稳定性更好。
2)绳阻尼对WDPR动力学响应的影响主要体现在响应幅值上,绳直径越大,绳阻尼对WDPR动力学响应的减振作用越明显。特别地,对于直径小于2mm的细绳来说,相比无阻尼的情况,绳阻尼对飞机模型位姿及绳张力的振荡频率和相位的影响很小,基本可以忽略。
3)当绳阻尼系数大于0.6 N·s/m时,不论绳直径粗细如何,其阻尼对WDPR动力学特性的影响不能忽略。
综上所述,本文提出的建模方法和研究结果可为WDPR的设计提供指导。此外,绳阻尼的非线性特征及其随不同参数的变化规律,将在今后进一步开展研究。

