空间多体系统轨道姿态及机械臂一体化控制
魏春岭,袁泉,张军,王梦菲
(1.北京控制工程研究所,北京100190; 2.空间智能控制技术国家级重点实验室,北京100190)
空间机器人是未来在轨服务任务中的实施主体,随着空间开发程度的提高,各国均发射了空间机器人进行空间操作任务演示,如日本的ETSVII、美国的“轨道快车”、XSS-10、XSS-11等[1-4]。
空间机器人是典型的空间多体系统,一般采用卫星本体基座与用于目标操作的机械臂组成,这种典型的空间多体系统自由度多、动力学复杂,给其控制带来了挑战。
目前,已经有一些文献进行了空间多体系统的控制研究。文献[5-6]针对目标捕获时如何减小机械臂对基座的干扰进行了机械臂控制器的设计;文献[7]在不进行轨道控制但同时对基座和机械臂姿态进行控制的情况下,设计了关节空间内的自适应控制器;文献[8-9]在既不进行基座轨道控制,也不进行基座姿态控制时,针对外干扰的不确定性,通过将工作空间内的状态转换到关节空间内,设计了工作空间内的自适应控制器;文献[10]在基座轨道停控但姿态受控时,针对机械臂在工作空间的操作控制,进行了基座姿态与机械臂的控制器设计;文献[11]针对基座完全停控与基座进行姿态控制进行了比较研究;文献[12]在只进行基座姿态控制时,通过广义Jacobi矩阵规划机械手的运动,可实现对基座的近似零干扰,该方法后来在ETS-VII上进行了试验。
从上述文献可以看到,空间机器人的控制器设计思路主要分为2种:一种是基座完全停控,即轨道和姿态都不施加控制,机器人只进行机械臂的关节控制,该方法相当于完全丧失基座的控制能力,机械臂末端可以达到的空间位置姿态非常有限;另一种是基座姿态施加控制,但轨道不进行控制,同时机械臂各关节施加控制,该方法利用了基座的3个姿态转动自由度,部分扩展了空间机器人的工作空间,但还是丧失了基座轨道控制后所能达到的工作空间。上述2种情况都只利用了机械臂和(或)基座的转动自由度,会导致机械臂可达空间有限,对于复杂的操作任务,常常还会导致机械臂构型奇异,无法完成操作任务。
本文突破传统方法中只对机械臂和(或)基座姿态进行控制的思路,在通用的空间多体系统的动力学模型基础上,对基座的轨道、姿态及机械臂的各个自由度同时进行协同控制,即利用系统的所有自由度来实现空间操作,相比以往机械臂对目标操作时基座停控的情况,理论上可以达到空间中的任意位置,彻底消除机械臂操作时的构型奇异问题,极大地增加了空间机器人的操作范围和工作空间,增强了机器人在轨实现各种复杂任务的能力。
1 动力学建模
空间机器人由基座及机械臂两大部分组成,如图1所示。
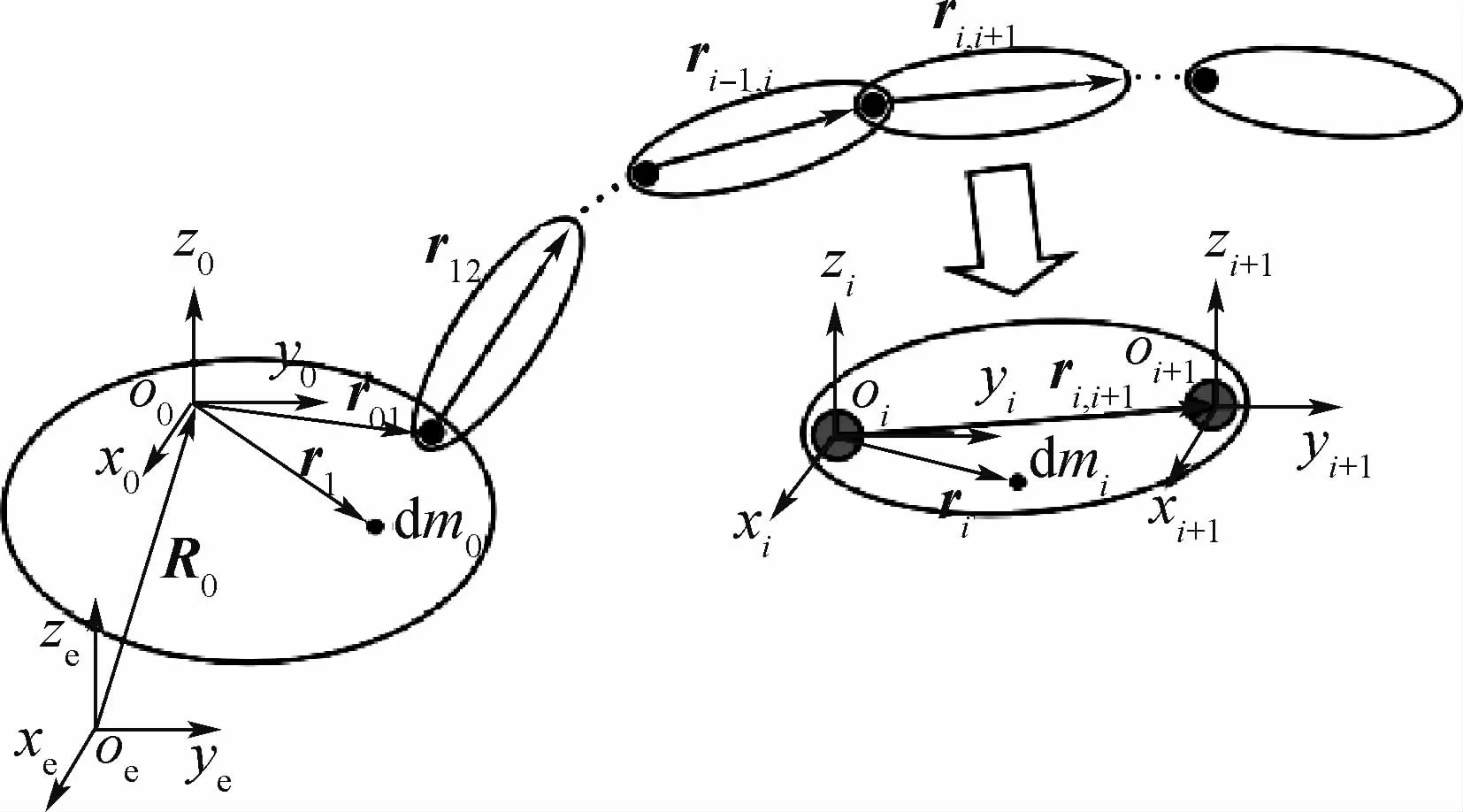
图1 空间机器人结构示意图Fig.1 Configuration illustration of space robot
为了对图1所示系统进行描述,定义如下坐标系:惯性坐标系oexeyeze,固定在惯性空间中;第i(0≤i≤n)体的本体坐标系oixiyizi,i=0对应基座,o0固定在基座的质心,i>0时对应各节机械臂,oi固定在第i体与i-1体的铰接处。该多体系统的动力学方程可表示为

在上述动力学方程的建立过程中,选取了基座的质心位置、基座的姿态及机械臂的各关节角度作为动力学方程的状态变量,与传统文献不进行基座的轨道控制相比,多出了基座质心的平动动力学方程。由于空间机器人在进行空间任务操作时,在基座本体上常常安装了全局相机,以对周边环境进行观察,通过本文基座质心,可以方便地计算出固定在基座上的相机的位置与姿态,从而对相机的观察模型进行数值建模与仿真。而传统文献由于不考虑基座的轨道运动,常常将系统的平动点取在整个系统的质心处,但由于空间多体系统的变构型特点,系统的质心没有固定的位置,因此也无法利用系统质心对基座上的全局相机等进行建模。
2 控制律设计
为了对空间机器人进行控制,选取需要控制的状态量为qE=[RT0θT0RTEθTE]T,注意qE与动力学方程中q的区别,R0、θ0、RE、θE分别为基座位置、姿态及机械臂末端位置、末端姿态。
为了描述基座的姿态运动,采用如下形式定义基座的姿态运动:

式中:θ0=[φ0θ0ψ0]T为基座的三轴欧拉角。
采用312转序时,D(θ0)可表示为
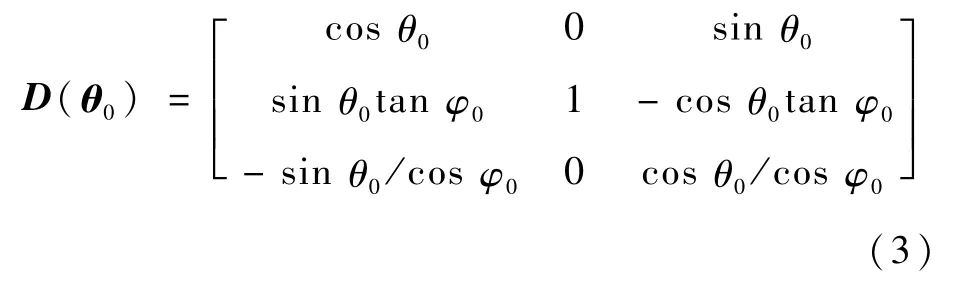
为了建立qE与q的关系,需要将机械臂末端的位置和姿态表示成机械臂各关节的函数。
第i体质心的速度可表示为

式中:Aek为从okxkykzk到oexeyeze的坐标转换矩阵;Ski为第i体相对第k体的静矩,即
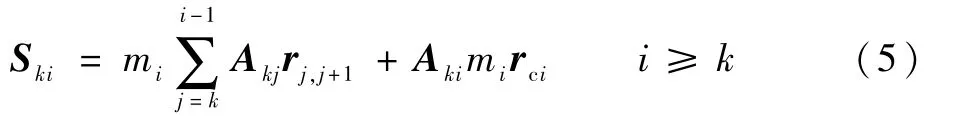
其中:Aki为从oixiyizi到okxkykzk的坐标转换矩阵;rj,j+1为从oj到oj+1的矢量坐标(见图1);rci为第i体质心在oixiyizi中的位置。
机械臂末端的速度可表示为
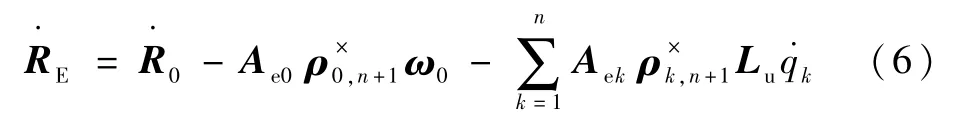
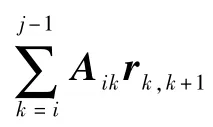
机械臂末端的角速度可表示为
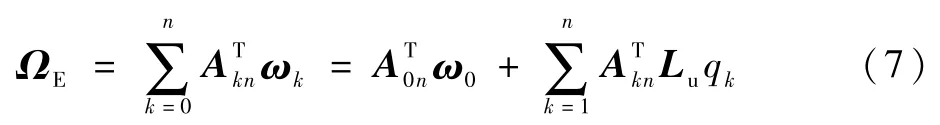
机械臂末端姿态的运动学也采用312欧拉角来描述,则
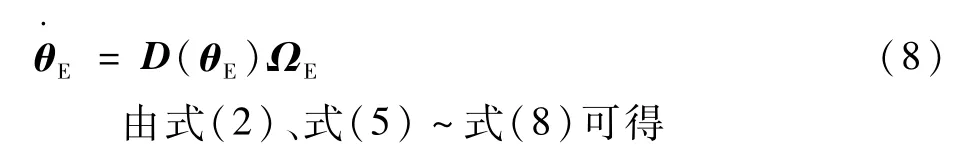

式中:J为Jacobi矩阵。式(9)即建立了控制状态量qE与动力学方程中的状态量q之间的关系。
式(9)中,当J不是满秩矩阵时,称为“动力学奇异”,出现动力学奇异时,空间机器人无法将机械臂末端在惯性空间中进行任意位置、姿态的跟踪。由于本文对空间机器人的基座位置、姿态及机械臂的各关节同时进行控制,最大程度上利用了空间机器人的所有自由度,因此可以将这种“动力学奇异”现象降低到最少,同时从物理意义上,由于基座的位置可控,因此可以将机械臂的末端定位到任意位置和姿态,即使遇到了这种“动力学奇异”现象,也可以在通过所谓的“零运动”,即在不改变末端位姿的情况下,基座和机械臂进行协调运动,将基座与机械臂的构型进行重构,脱离出奇异构型。
“动力学奇异”与系统的当前状态相关,从理论上,永远无法完全消除这种现象,所以本文对逆矩阵J-1采用J的Moore-Penrose逆J+来代替,J满秩时二者相等,J奇异时,J+则可有效避免高幅值的关节角速度指令。从后文仿真来看,采用本文的控制方法,未遭遇到奇异构型。
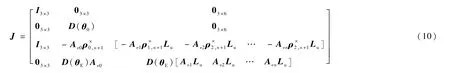
下面针对控制状态量qE进行系统跟踪控制器设计。
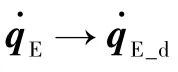

选取如下形式的Lyapunov函数:

对式(12)求导,选取如下控制律:

式中:K1为控制增益。
由式(13)可解得


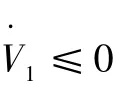

因此系统是渐近稳定的。

在式(12)基础上进一步取如下形式的Lyapunov函数:

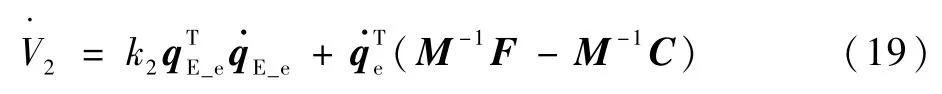
由式(11)、式(13)与式(16)可得如下等式:

将式(19)代入式(18)可得
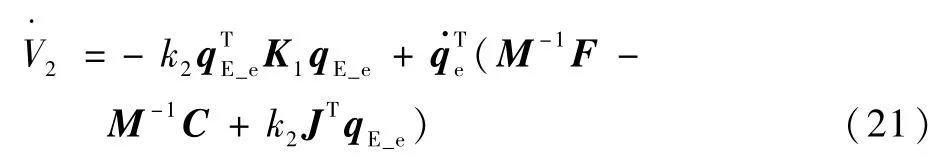
取
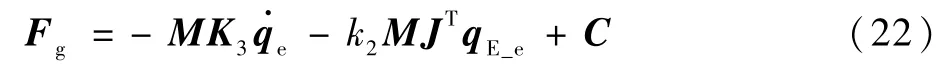
式中:K3为控制增益。
则
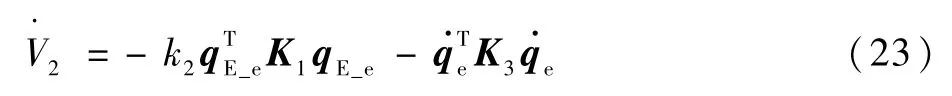
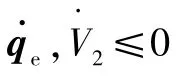

即采用式(22)中的控制输入时,系统是渐近稳定的。
将式(14)和式(16)代入式(22)可得最后的控制输入为
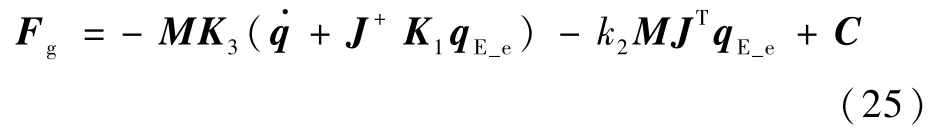
式(25)即为整个系统的控制输入,包括基座位置控制力、姿态控制力矩与机械臂各关节的控制力矩。
3 轨道控制脉宽调制

图2 伪速率调制器框图Fig.2 Block diagram of pseudo-rate modulator
式(25)给出的是连续控制指令,而对于轨道控制来讲,采用的是喷气发动机;基座的姿态控制可以采用喷气发动机,也可以采用角动量交换执行机构,如控制力矩陀螺;机械臂的关节控制采用伺服电机。本文中只利用喷气进行基座的轨道控制,基座的姿态控制采用能输出连接指令的控制力矩陀螺。因此,利用发动机的固定推力器来实现轨道的控制,需要将上述连续指令调制成离散脉宽。现有多种指令调制方法,而本文采用常用的伪速率调制方法进行脉宽调制,其形式如图2所示。将三轴轨道控制指令F1、F2、F3输入到伪速 率调制器,hA、hE、KM、TM均为伪速率调制器的设计参数,Fmax(针对三轴分 别为Fmax1、Fmax2、Fmax3)为该轴发动机能提供的喷气力。通过伪速率调制器的调节,即可将连续指令调制成离散脉宽,并在系统姿态控制性能上近似等价。伪速率调制器不是本文的重点,具体设计可参见文献[15]。
4 数学仿真
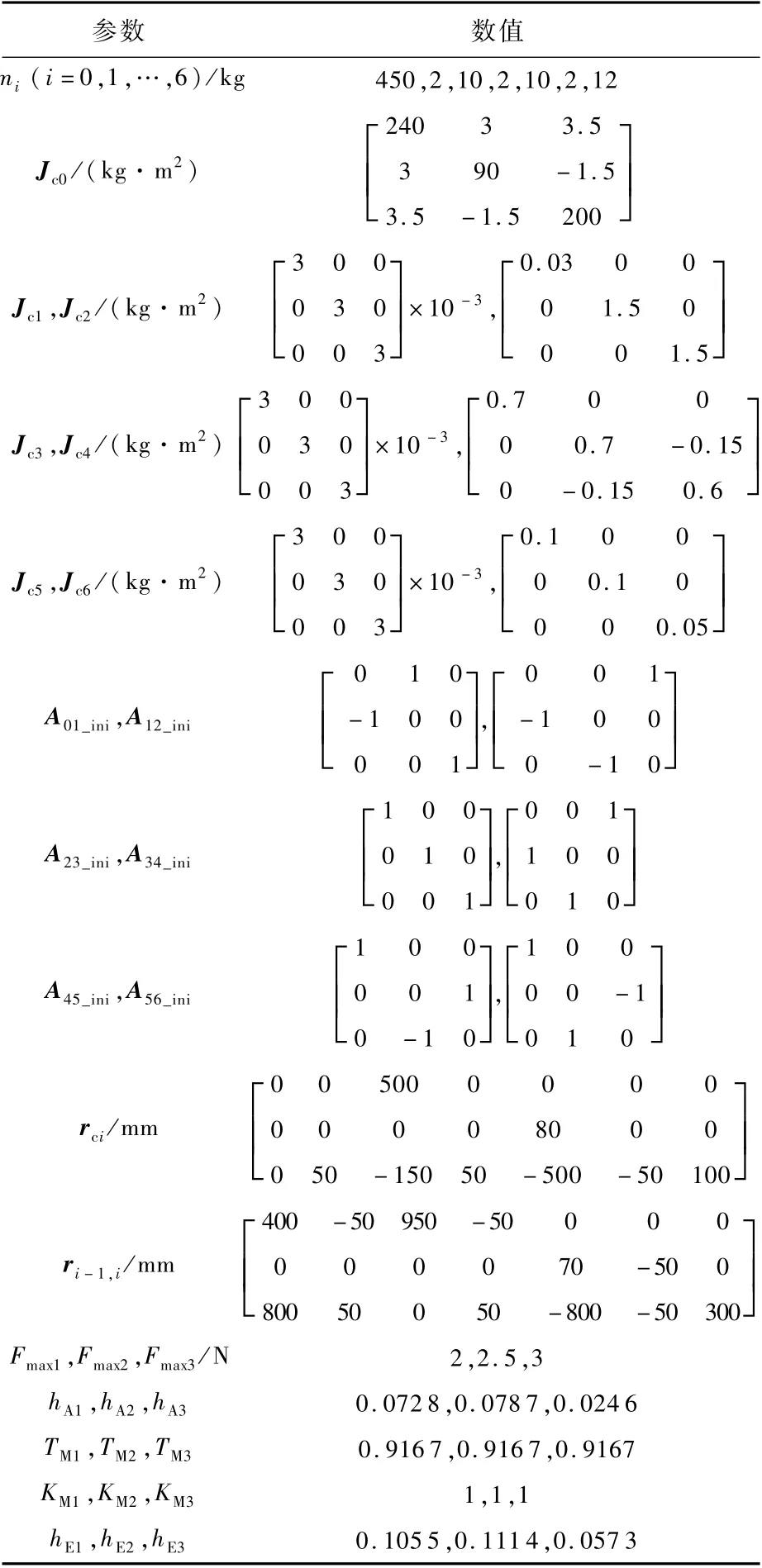
表1 系统动力学与控制仿真参数Table 1 Parameters of system dynamics and control simulation
为了对控制律的性能进行验证,以某空间机器人为对象进行建模与仿真,假设空间机器人的机械臂具有6个关节自由度。式(25)中的控制增 益K1、k2、K3分 别 取2.5×10-5I12×12、0.7、0.25I12×12。空间机器人基座及各节机械臂的质量特性参数及尺寸见表1,表中Jci为第i体相对其质心的转动惯量,设空间机器人初始时机械臂处于收拢状态,即各关节转角为0°,Ai-1,i_ini为从第i体到第i-1体的初始坐标转换矩阵。
控制目的是:使基座位置控制到[0.5 0.6 -0.3]m,基 座 姿 态 机 动 到[-12 10 0]°;机械臂末端在oexeyeze内位置达到[0.6 -0.2 0.8]m,在oexeyeze内姿态达到[15 -30 60]°。
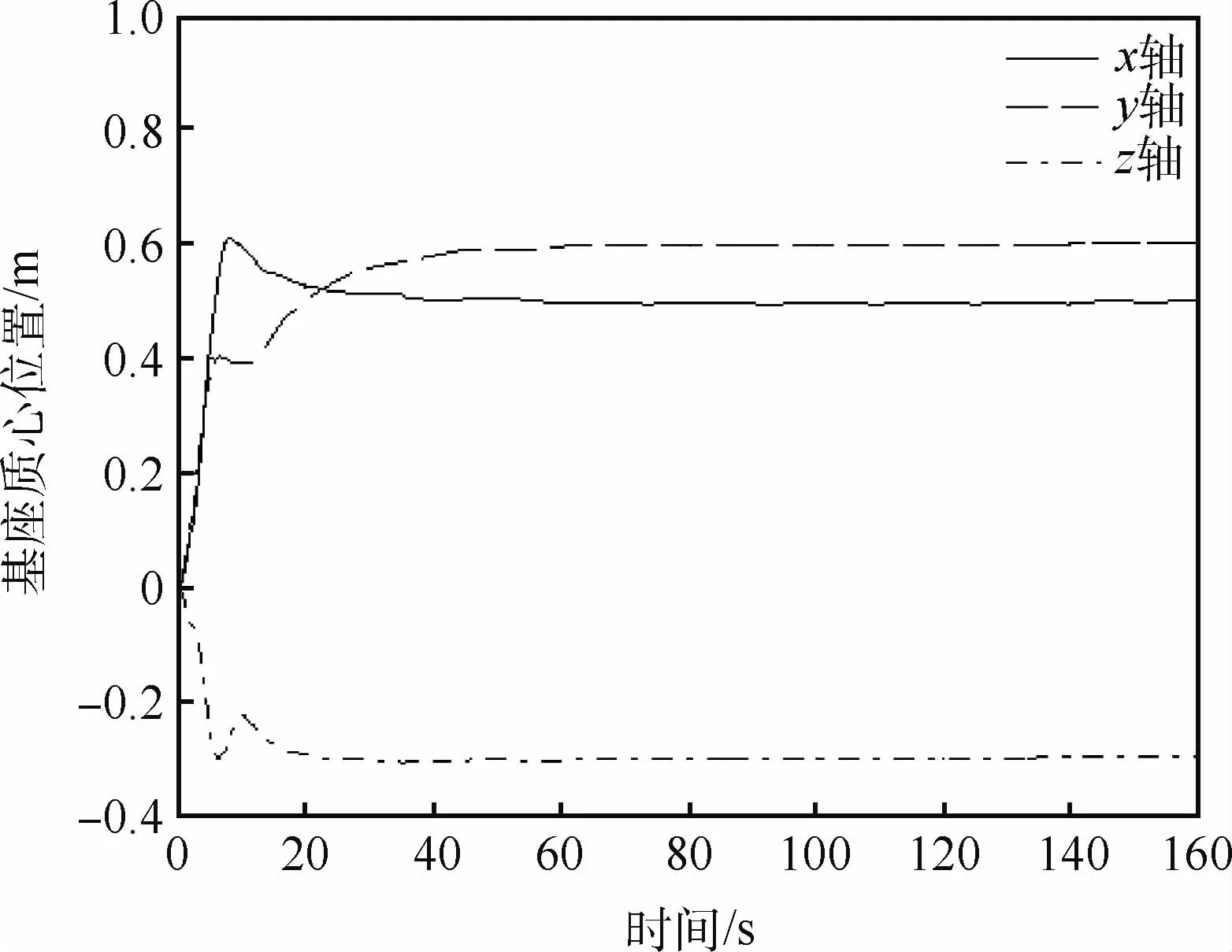
图3 轨道变化(基座质心o0 位置)Fig.3 Orbit variation(position of mass center o0 of base of robot)
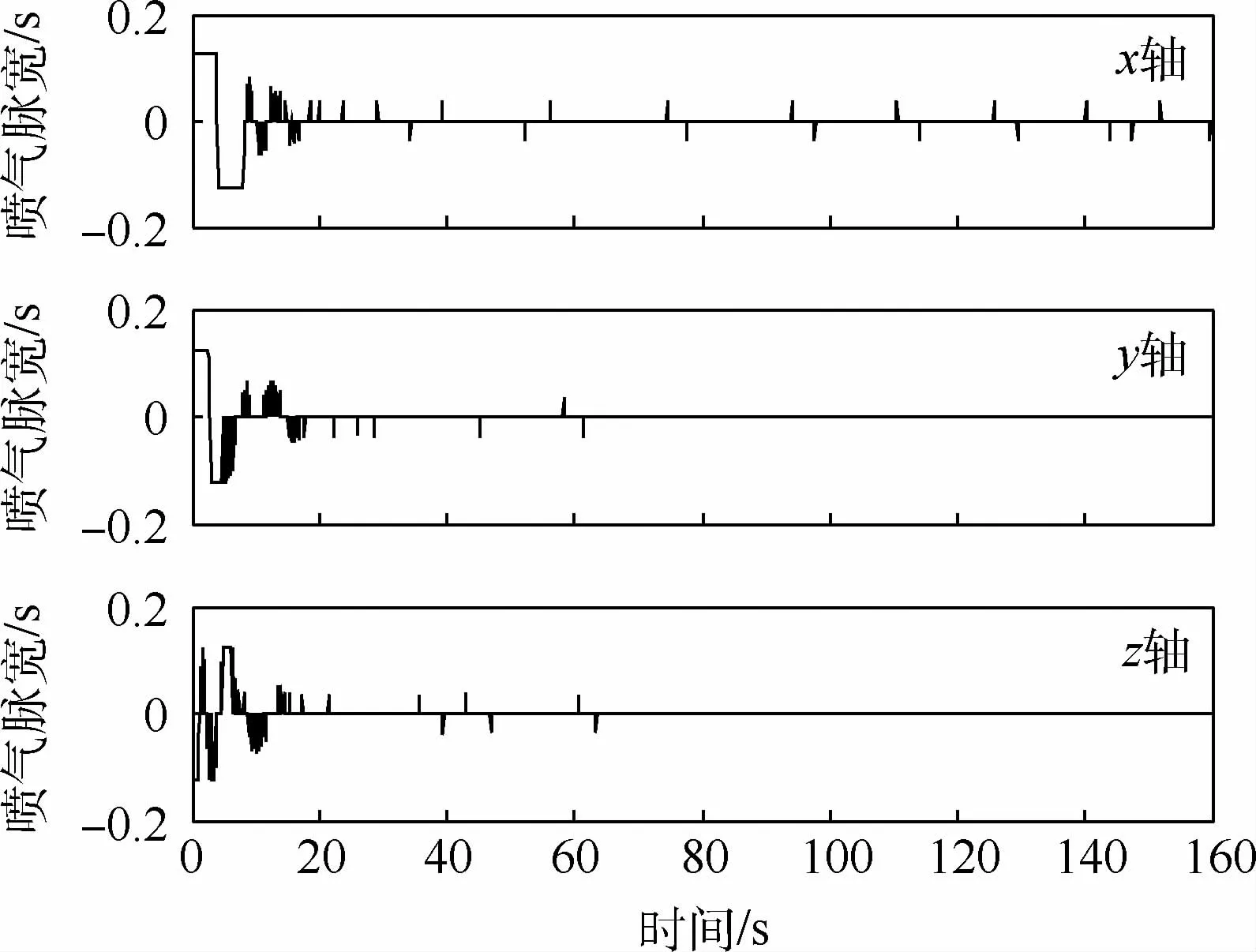
图4 轨道控制发动机喷气脉宽Fig.4 Jet impulse width of orbit control engine
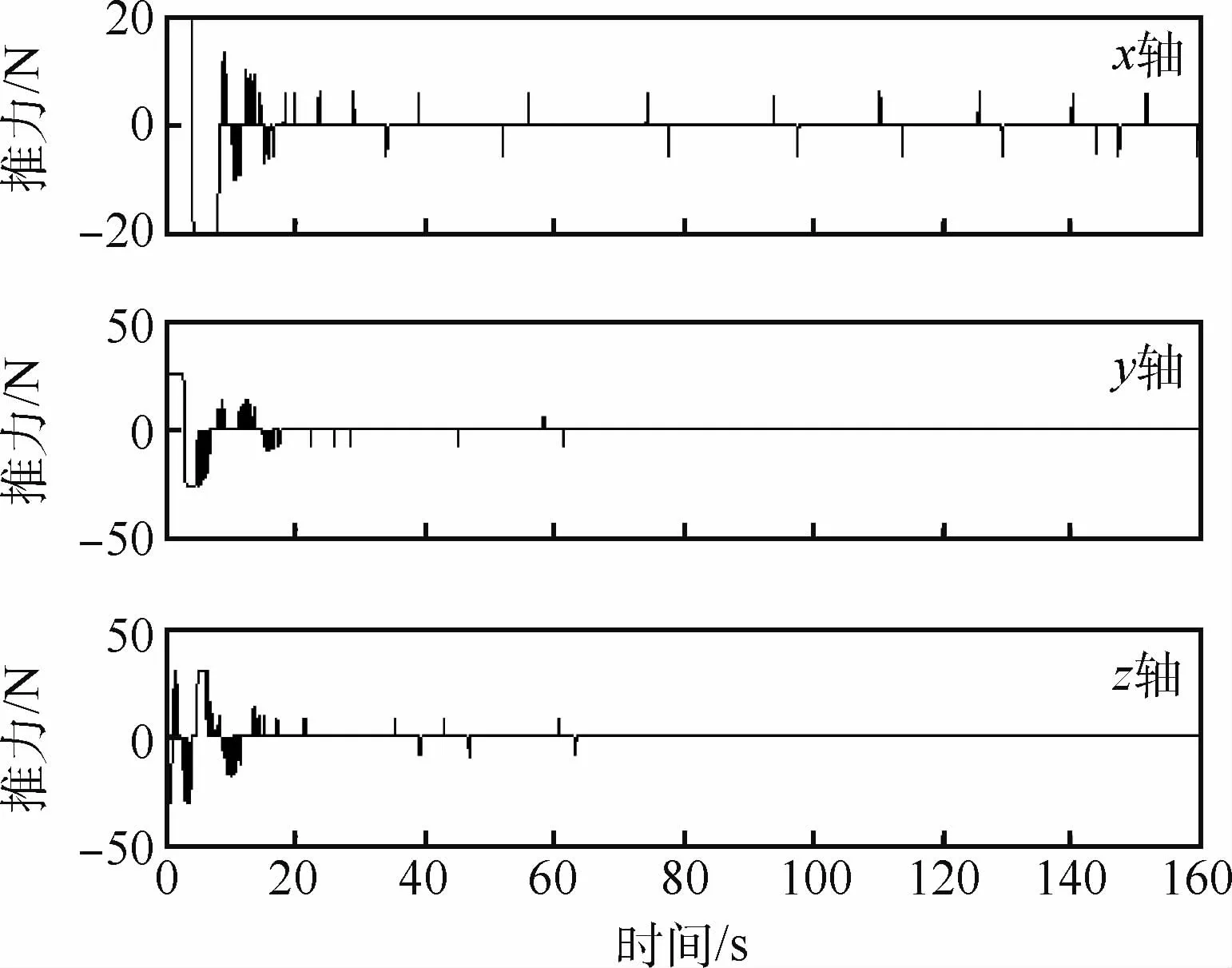
图5 轨道控制发动机喷气脉宽换算出的推力Fig.5 Thrust calculated from orbit control engine jet impulse width
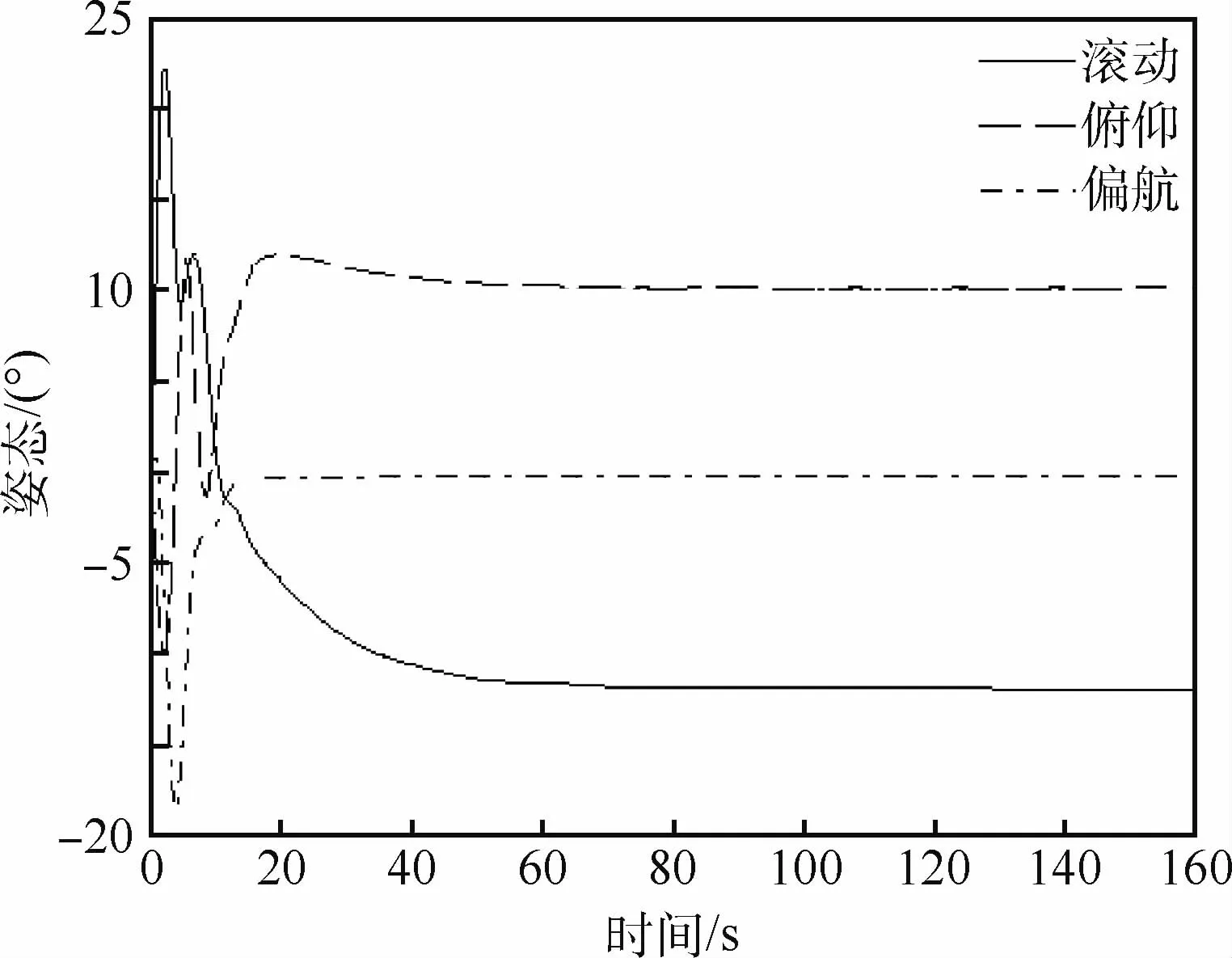
图6 基座三轴姿态Fig.6 Triaxial attitude of base of robot
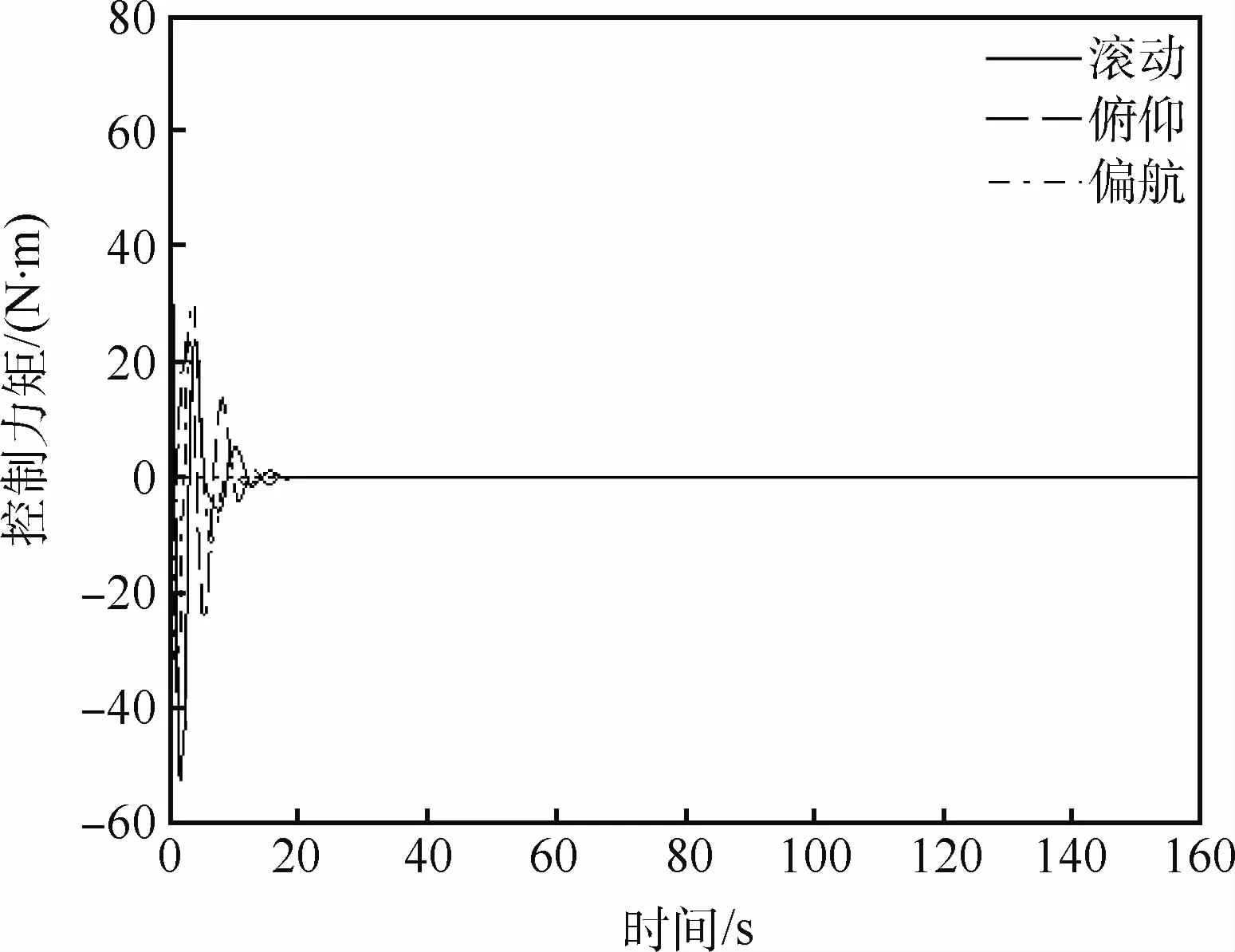
图7 基座三轴控制力矩Fig.7 Triaxial control torque of base of robot
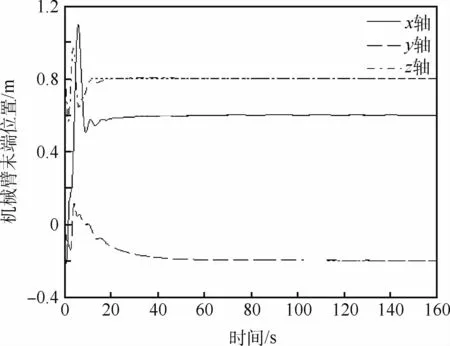
图8 机械臂末端在惯性空间中的位置Fig.8 Position of arm tip of manipulator in inertial space
仿真结果如图3~图11所示。图3为轨道控制曲线,即基座质心的位置曲线,从图中可以看到,约60 s后,轨道位置到达期望的位置。图4为轨道控制发动机喷气脉宽。图5为由脉宽换算成的轨控推力,实现了由喷气脉宽对发动机连续指令的调制。图6为基座的三轴姿态,约70 s后,星体机动到期望的目标姿态。基座的姿态控制力矩如图7所示,在动态过程中其最大峰值约为60 N·m,该力矩可采用控制力矩陀螺来实现,约20 s后趋于稳定。图8为机械臂末端的位置,约5 0 s后逐渐趋于指令值。图9为机械臂末端在惯性空间中的姿态,也趋于期望姿态。图10为机械臂各关节角曲线。图11为机械臂6只关节的控制力矩,其幅值也在可以接受的范围内。
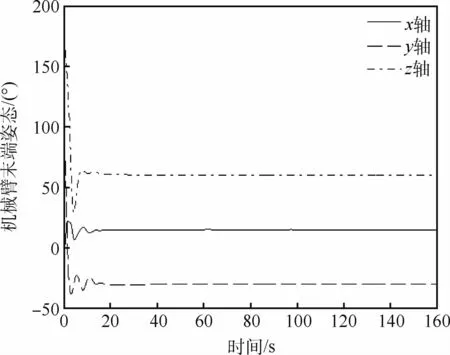
图9 机械臂末端在惯性空间中的姿态Fig.9 Attitude of arm tip ofmanipulator in inertial space

图10 机械臂关节角Fig.10 Joint angles of manipulator
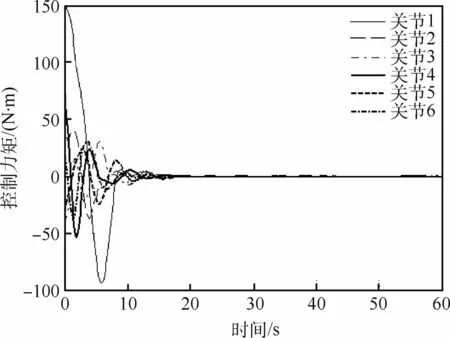
图11 机械臂关节控制力矩Fig.11 Control torque of joints of manipulator
传统的方法对基座的轨道和(或)姿态不施加主动控制,基座的轨道、姿态将只能随机械臂关节的运动而被动变化,在本文中,通过对基座的轨道和姿态同时进行控制,将基座的位置、姿态控制到期望状态,就能有效利用基座的平动和转动自由度,与机械臂各关节协同,实现机械臂末端的精确控制。
仿真显示,采用本文设计的一体化控制器,能同时实现空间机器人基座的轨道、姿态和机械臂位置、姿态的精确控制,并使系统具有较好的动态特性。
5 结 论
空间多体系统在未来新型空间任务中具有重要应用价值,值得大家广泛关注与研究,本文所做的工作和得到的结论如下:
1)针对空间多体系统的轨道、姿态及操作机构进行了建模,并针对解析的系统模型,设计了基座轨道、姿态及操作机构的一体化控制器。相对于基座的轨道或姿态不施加控制的传统方法,本文控制器充分利用了空间多体系统的所有自由度,能实现所有自由度的主动控制,从而扩展了空间多体系统的工作空间。
2)设计的控制器能使空间机器人同时进行大范围的轨道转移、姿态机动,同时操作机构可进行末端快速精准操作,满足快速、同步、协调的高性能要求,通过完整的空间多体系统动力学与控制仿真建模,验证了本文控制器设计方法的有效性。

