高中物理“板—块”模型浅析

郭次茂

摘  要：“滑块—木板”模型是高中物理中很重要的模型之一，其中涉及到板块能否被视为一个整体的判断，板块发生相对运动时如何求板块长度，板块在一定的条件下共速后只在摩擦力作用下的运动情况分类分析，以及使用动能定理、动量守恒定律求解板块问题。

关键词：“滑块—木板”;摩擦力;牛顿第二定律;整体

在高中物理学习过程中会出现很多的物理模型，比如力学分析中的杆模型，动力学部分的传送带模型，动量守恒定律中的人船模型。同学们在学习过程中要抓住各个模型的本质特点，受力情况及运动过程，达到举一反三，以不变应万变的能力。

“滑块—木板”模型是力学中最常见的模型之一，是历年高考的热点内容。在“滑块—木板”模型问题中，摩擦力的分析非常重要，特别是板块间的摩擦力，如果板块相对静止一起加速运动，则它们之间是静摩擦力，而静摩擦力会在一定范围内变化，这样就出现了如何去判定板块在某一个外来作用下能否被视为整体。如果板块发生了相对运动，则板块之间是滑动摩擦力。在该模型中板块往往做匀变速直线运动，解决此类问题要抓住板块间的位移、速度、时间关系。解决此类问题的关键是找准相关的临界条件，滑块不从木板的末端滑下来的临界条件是滑块到达木板末端的时候板块恰好共速。板块模型的实质是解决板块间的相对运动问题，要找到板块各自对地的位移，再求它们之间的相对位移。

一、板块在水平拉力作用下由静止开始运动

关键是判定板块中谁的加速度有最大值，通常靠摩擦力提供动力的物体加速度有上限，既受摩擦力和拉力的物体的加速度没有上限，加速度将随外力的变化而变化。

（一）如图1力F作用在木块上，m与M之间的摩擦因素为u1，M与地面间的摩擦因素为u2

1.如果u1小于或等于u2，则m的加速度没有最大值，可以随着F的增大而增大，遵从F-u1mg=ma1，对木板由于木块对它的摩擦力u1mg小于地面对它的最大静摩擦力u2（m+M）g。故木板始终保持静止状态。

2.如果u1大于u2且如果满足u1mg大于u2（m+M）g，则在F逐渐增大的过程中，F先达到u2（m+M）g，该过程中整体保持静止，然后随着F的增大整体一起加速前进，对板块整体满足F-u2（m+M）g=（m+M）a，则块对板的摩擦力为静摩擦力f，满足f-u2（m+M）g=Ma2。当f达到最大值u1mg时M的加速度为最大值。此后对块遵从F-u1mg=ma1，板遵从u1mg-u2（m+M）g=Ma2。

（二）如图2力F作用在木板上，A与B之间的摩擦因素为u1，B与地面间的摩擦因素为u2

在F逐渐增大的过程中，F先达到u2（m+M）g，该过程中整体保持静止，然后随着F的增大整体一起加速前进，对板块整体满足F-u2（m+M）g=（m+M）a，则B对A的摩擦力为静摩擦力f，满足f=ma1。当f达到最大值u1mg时A的加速度为最大值故此过程中A有最大的加速度u1g，当A、B发生相对运动后对B满足：F-u2（m+M）g-u1mg=Ma2。

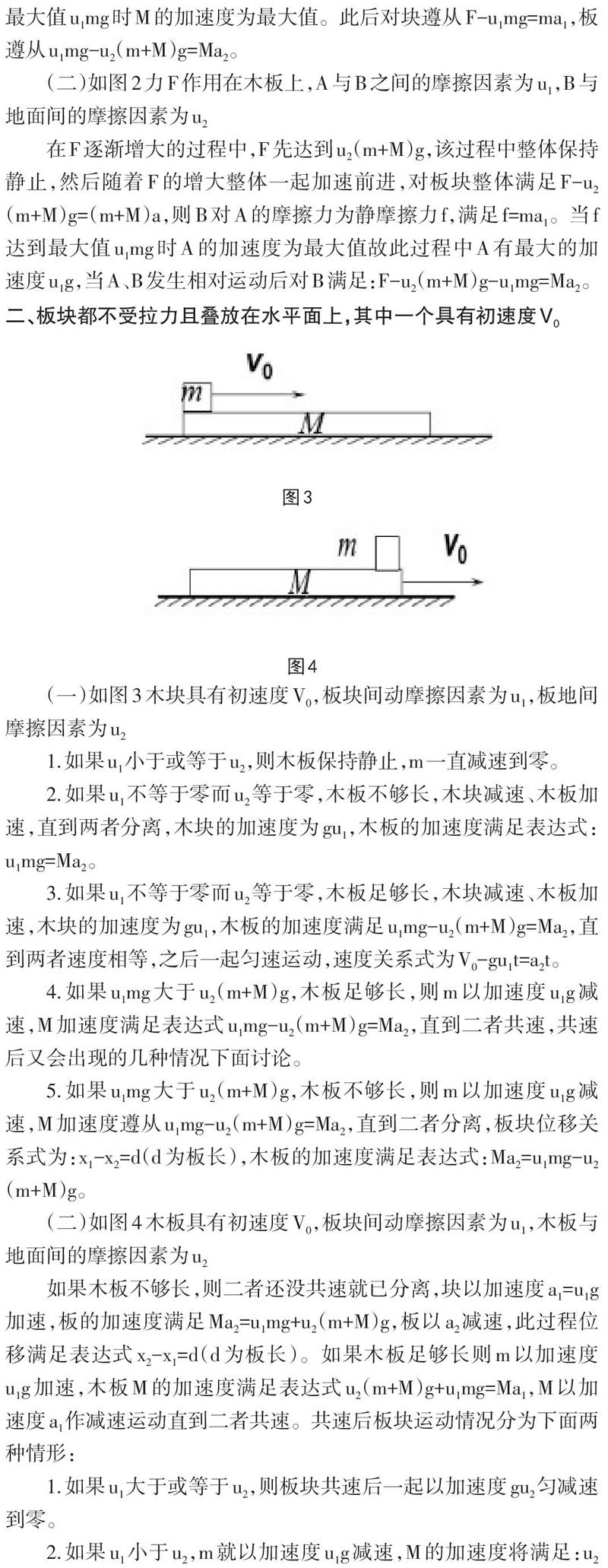
二、板块都不受拉力且叠放在水平面上，其中一个具有初速度V0

（一）如图3木块具有初速度V0，板块间动摩擦因素为u1，板地间摩擦因素为u2

1.如果u1小于或等于u2，则木板保持静止，m一直减速到零。

2.如果u1不等于零而u2等于零，木板不够长，木块减速、木板加速，直到两者分离，木块的加速度为gu1，木板的加速度满足表达式：u1mg=Ma2。

3.如果u1不等于零而u2等于零，木板足够长，木块减速、木板加速，木块的加速度为gu1，木板的加速度满足u1mg-u2（m+M）g=Ma2，直到两者速度相等，之后一起匀速运动，速度关系式为V0-gu1t=a2t。

4.如果u1mg大于u2（m+M）g，木板足够长，则m以加速度u1g减速，M加速度满足表达式u1mg-u2（m+M）g=Ma2，直到二者共速，共速后又会出现的几种情况下面讨论。

5.如果u1mg大于u2（m+M）g，木板不够长，则m以加速度u1g减速，M加速度遵从u1mg-u2（m+M）g=Ma2，直到二者分离，板块位移关系式为：x1-x2=d（d为板长），木板的加速度满足表达式：Ma2=u1mg-u2（m+M）g。

（二）如图4木板具有初速度V0，板块间动摩擦因素为u1，木板与地面间的摩擦因素为u2

如果木板不够长，则二者还没共速就已分离，块以加速度a1=u1g加速，板的加速度满足Ma2=u1mg+u2（m+M）g，板以a2减速，此过程位移满足表达式x2-x1=d（d为板长）。如果木板足够长则m以加速度u1g加速，木板M的加速度满足表达式u2（m+M）g+u1mg=Ma1，M以加速度a1作减速运动直到二者共速。共速后板块运动情况分为下面两种情形：

1.如果u1大于或等于u2，则板块共速后一起以加速度gu2匀减速到零。

2.如果u1小于u2，m就以加速度u1g减速，M的加速度将满足：u2（m+M）g-u1mg=Ma2，木板以加速度a2先减速到零。

三、板块都不受拉力且叠放在水平面上，两个物体都具有初速度V1、V2

1.如果V1、V2方向相同，如果木板不够长则分离，根据牛二定律明确各自的加速度，再根据板长确定位移关系最终求出分离时间等其它物理量;如果木板足够长则二者会共速，共速后再根据u1、u2的关系确定是否一起减速。

2.如果V1、V2方向相反，如果木板不够长则分离，根据牛二定律明确各自的加速度，再根据板长确定位移关系最终求出分离时间等其它物理量;如果木板足够长则其中一个物体速度先减小到零再反向加速直到二者共速，共速后再根据上面提到的情况分析。

四、使用功能关系、动能定理，动量守恒定律的角度去解决板块问题

我们从动力学的角度梳理了板块间的运动情况及解决方法，其实在学习了功、动能定律、动量的知识后，我们可以从动能定理，动量守恒定律的角度去解决板块问题。比如说板块间发生相对运动时，克服相对位移摩擦力做的功等于系统内能的增量，如果板块组成的系统水平方向不受外力或者合外力为零，则系统水平分向动量守恒，在板不够长时我们可以使用动量守恒定律求板块分离时的速度。如果板足够长二者最终共速可直接使用动量守恒定律轻松解决。

例如：一木块质量m1为2Kg，以V1等于5m/s的速度滑上一置于光滑水平桌面的木板上，木板质量m2为4Kg，初速度V2等于5m/s，木板恰好没离开木板，板块间的摩擦因素为0.2，求木板的长度是多少？

由于板块在水平方向不受外力，故板塊组成的系统水平方向动量守恒，由于二者恰好不离开的临界条件是二者共速，我们可使用动量守恒定律：m1V1+m2V2=（m1+m2）V共可得共同速度为3m/s，再根据动能定理可以求出木板的长度，当然本题我们也可以从动力学的角度使用牛二定律，再结合运动学公式解答。

当然我们上面提到的板块模型是较简单、过程较少的情况。如果涉及多过程板块模型，在每一个过程中必须重新对板块各自进行受力分析、运动分析，特别是摩擦力是否为滑动摩擦力，摩擦力对谁充当动力还是阻力，再用牛二定律求出各自的加速度，然后解决相关问题。如果能从多角度解决板块模型，应根据具体情况而定。

在学习过程中，我们会遇到与板块模型处理方法相似的模型，比如传送带模型，子弹打木块模型，板块模型除了在水平面外，在斜面上也存在板块模型，解决方法类同。在教学的过程中引导同学们多思考、多总结，熟悉各种物理模型，从而不断提升同学们的物理思维、解题能力，达到事半功倍的效果。