基于NAO机器人的行走约束研究
,,
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
0 引言
从20世纪中后期早稻田大学制造出WABOT-1型机器人开始,人们对人形机器人的研究一直在不断进步。2000年本田公司制造ASIMO机器人,随后又在2011年推出了全新的ASIMO以及人形机器人HRP-4C和Robonaut2[1]。几年后,NAO机器人的横空出世可见人形机器人的发展之快,而本文以NAO机器人进行研究。
对于人形机器人的运动轨迹研究有几种方法,如以动力学分析为基础的步行规划方法[2];基于捕捉人体运动的步态规划方法[3];基于ZMP理论的步态规划[4];基于被动步行的步态生成方法[5];基于倒立摆模型的方法[6];基于能量最优化的方法[7];基于多连杆模型的方法等[8]。此前方法多数已经成功而且应用在实际的机器人上[9-11]。
然而以上研究,机器人的骨盆运动与自由足所受到的限制并未纳入考虑范围,因此无法完全控制零力矩点(ZMP)从而无法保证机器人稳定的行走。基于此提出约束行走规划,使机器人的脚与地面充分接触,即使由于机器人行走过程中骨盆运动和自由足所受到的限制,也能实现机器人的稳定行走。
1 NAO机器人及运动学分析
NAO机器人是由Aldebaran机器人公司制造的可编程人形机器人。具有25个自由度,每只手臂5个、每个脚1个、头部2个、腿部11个;身高0.57 m,体重4.5 kg。该机器人如图1所示。其腿部的运动模型如图2所示。每条腿上有6个旋转关节,但由于关节与骨盆相连,其运动会受到限制,而上面有1个制动器来产生对称旋转。

图1 Aldebaran公司NAO仿人机器人
为了更好地理解NAO机器人的运动模式,采用改良的D-H参数法(Denavit和Hartenberg参数法)对NAO机器人腿部建立运动学模型。每个连接处都附上一个正交参考坐标系。连接点的编号为0~12,从固定连接点开始(支撑足),到移动脚(自由足)结束,如图2所示,能够看出正交坐标系XM,YM和ZM是建立在地面坐标(全局坐标系)上。
为了展开运动分析,在同一个运动链上建立了2套参考坐标系:一个是针对右侧固定足(frf),另一个是针对左侧固定足(flf)。图2中显示的运动链是右侧固定足。对于frf和flf来说,坐标系编号都从零开始,指定到固定足。表1列出了腿部运动链的改良后D-H参数。这些参数对于frf和flf 2条链来说都是一样的。表1中非空距离数值为d3=d11=0.103 m,d4=d10=0.10 m,r6=r7=0.071 2 m。
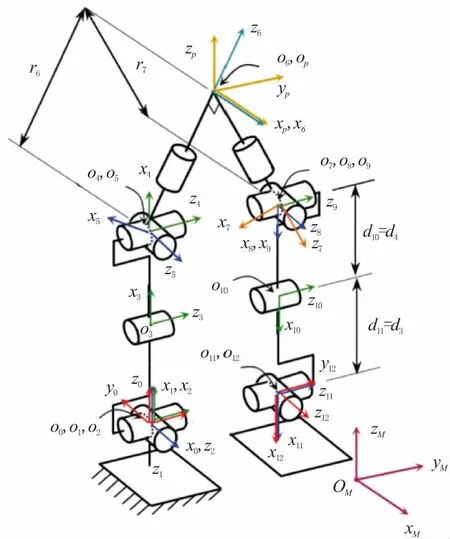
图2 NAO机器人腿上的运动坐标系示意
各个连杆和关节处的局部坐标系的设定方法是:与连杆或是关节i相关的坐标系成为坐标系{1}其中i=1,2,…,12。αi表示绕Xi轴,从Zi旋转到Zi+1的角度;
di表示绕Zi轴,从Xi-1移动到Xi的距离;
θi表示绕Zi轴,从Xi-1旋转到Xi的角度;
τi表示骨盆到左右连杆水平延长线的距离。
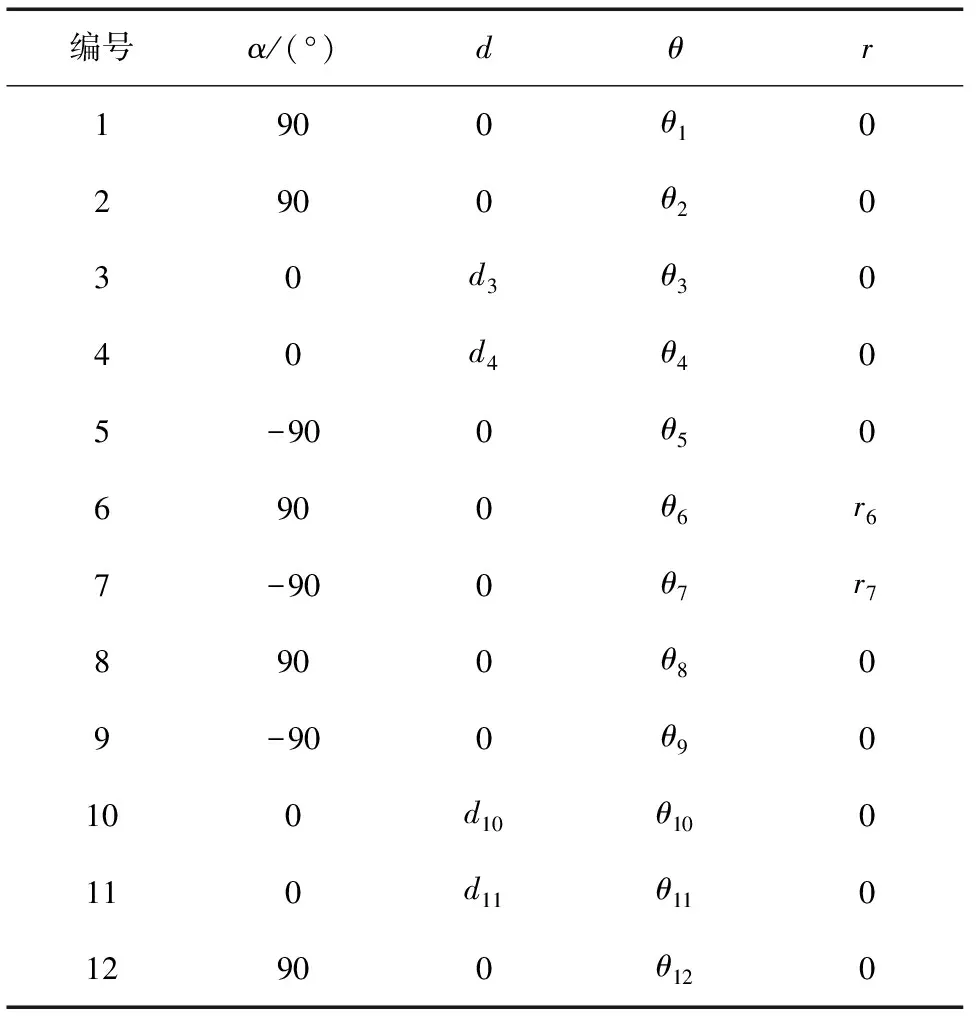
表1 改进后NAO双腿的D-H参数
根据图3所示的动力传输结构能够看出一个简单的电机如何为运动链骨盆上的关节6和关节7提供运动。因此,以下约束来自动力传输θ6=θ7。
移动状态下的机器人明显约束了运动链的机动性,这时候方程式成立。由图3可知,附着于骨盆的一个正交参考坐标系(参考坐标系xp-yp-zp)。
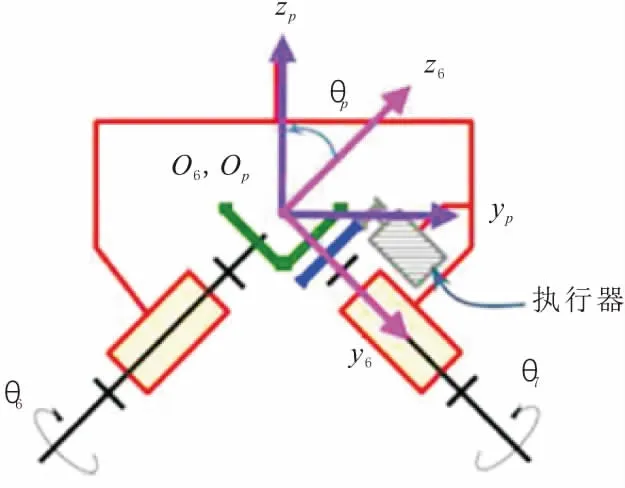
图3 向附着于骨盆的关节传输动力的结构
这个坐标系通过固定角θp相对于坐标系6的x6轴转动。其中,frf的θp=45°,而flf的θp=-45°。
2 NAO机器人行走规划
规定附着于骨盆(坐标系xp-yp-zp,如图2所示)的坐标系姿态(位置与方向)以及相对于全局坐标系的自由足(坐标系x12-y12-zp12)作为时间函数,以此定义正常行走模式。当行走过程中,坐标系xp-yp-zp保持平行于坐标系xm-ym-zm,而且自由足脚底保持平行于全局坐标系的平面xm-ym时,就能够获得人形机器人的一个特定行走情形。这种行走就是本文中所定义的基本行走。
在这种行走情形下,躯干的位移仅限于平移,而自由足则是普通运动,而且受限于围绕的旋转运动。可利用与全局坐标系相匹配的本坐标系开始处相应连接点附着的Bryant角度λ,μ和υ,来规定骨盆与自由足相对于全局坐标系的理想方向。因此,在基本行走模式中,骨盆的3个Bryant角度都是零位,因此骨盆相对于全局坐标系的旋转矩阵为

(1)
对于正常行走模式中的自由足转动,规定足部坐标系中矢量x12的方向。为了保持基本行走的条件,这种矢量必须与地面(平面xm-ym)相交。因此,自由足相对于全局坐标系的旋转矩阵为
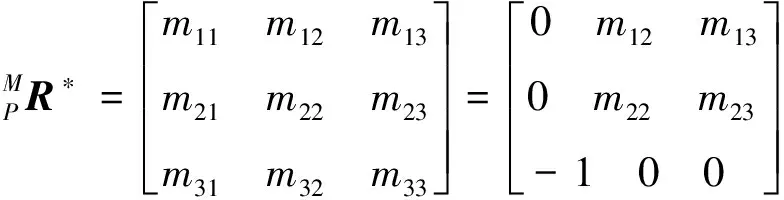
(2)
矩阵中的m12,m22,m23等项的定义取决于λ,μ,υ的赋值。在之前有关基本行走模式的分析中,已经证明对于骨盆特定姿态和自由足特定位置,m12,m13,m22,m23必须符合以下方程式要求,即
-c7s8m13+(cPc8+sPs7s8)m23=0
(3)
(4)
Si=sinθici=cosθi(i=7,8);sP=sinθP;cP=cosθP。θ7和θ8分别是图2所示运动链中关节7和关节8的关节变量。
对于基本行走模式来说,自由足的Bryant角度受到约束,其中m12,m13,m22,m23符合式(3)和式(4),这些方程式被定义为基本行走模式的前提条件。在行走过程中,如果骨盆的OP点路径保持在机器人矢状平面上,而自由足的点O12保持在与矢状平面平行的平面上,就能够达到上述前提条件。否则,自由足的脚底就不会平行于地板平面,继而无法实现足部与地面的稳定接触。
3 行走约束条件
对于NAO机器人的基本行走模式来说,可以实现支撑足的姿态下,让脚底与地面充分接触。但是在基本行走模式中,骨盆点OP受到约束,保持在矢状平面上。这种条件下,单独支撑阶段中的ZMP一般无法保持在机器人的支撑表面上。
为了全面控制ZMP的位置,必须让点OP的运动构件保持在正面。然而,这样一个构件会避开基本行走;因此,如果想要改善支撑足脚底中ZMP的位置,必须忽略基本行走的前提条件。提出保持支撑足的充分接触状态(式(2)),但却允许骨盆在正面旋转与位移。
因此,自由足的位置与方向以及骨盆位置将会被完全指定。骨盆可以旋转,这样能够改善自由腿的机动性,以便适当控制ZMP。为了规定自由足的方向,采用Bryan角度λ12,μ12和v12来定义坐标12相对于全局坐标系的方向。骨盆方向的Bryan角度λp,μp,vp取决于支撑足的关节变量θ4,θ5,θ6。因为λp,μp,vp未明确,所以将θ4,θ5,θ6视为一种优化方法的自变量。
事实上,为了仅通过机器人部分规定运动中的11个自由度解决逆向运动问题,提出一个基于非线性优化方法的数值方案。该方案的各阶段划分如下:分别规定骨盆中点OP和附着于自由足坐标系中点O12的笛卡尔坐标xpypzp和xo12yo12zo12,以及规定相对于全局坐标系的坐标系12方向的Bryant角度λ12,μ12,v12。提出关节变量的初始值θ4,θ5,θ6。从提出的初始值θ4,θ5,θ6开始,将以下目标函数最小化,即
(5)
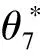
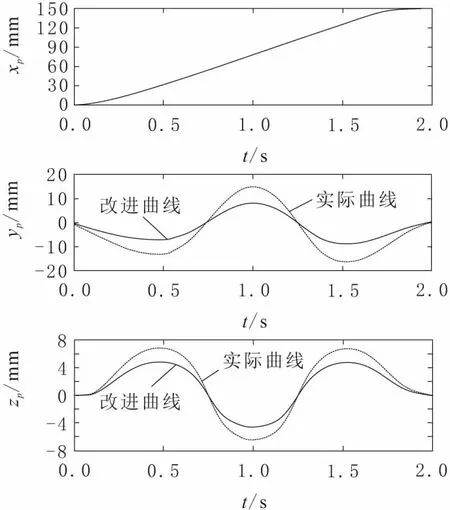
图4 骨盆的运动

图5 双足位置

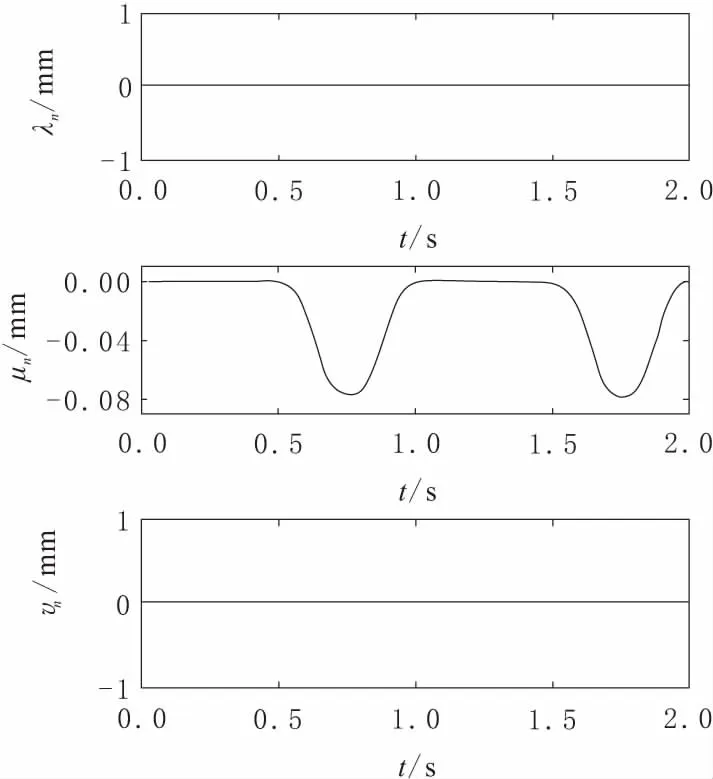
图6 右足的方向
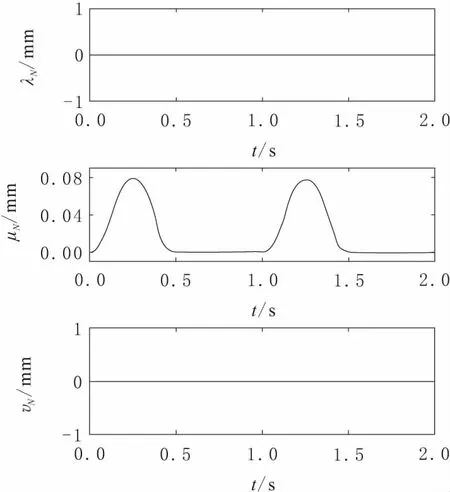
图7 左足的方向
4 仿真结果
在图4和图7中展示出相对于在限定条件下的骨盆和自由足的理想运动曲线。通过ZMP轨迹曲线来确定对骨盆运动的限制改善单支撑阶段的ZMP控制,先计算ZMP轨迹,结果如图8所示。
根据图8所示,实际ZMP曲线与理想曲线在部分地方差别较大,但通过限制骨盆移动后,在部分区域使之与理想曲线更加重合接近。

图8 ZMP曲线
如图9所示,对骨盆和自由足的理想运动通过加以规定,仅对骨盆的旋转运动进行合成。特定行走时间为每步0.5 s。行走包含4步,第1步相当于起始阶段,而最后一步为结束阶段。第2步和第3步处于匀速的巡游阶段。表2为各行走阶段数据,图9表示模拟状态下机器人各部行走的状态。从1 s开始时自由足与固定足的切换,直到2 s结束时,机器人的稳定状态模拟图像。

表2 约束后理想运动的各部分参数值
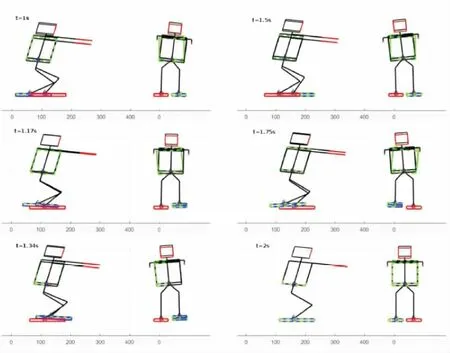
图9 行走模拟
5 结束语
当规定的Bryant角得到约束就能够实现机器人的持续运动以及每一步中自由足与地面之间的稳定接触。这样有助于解决NAO仿人机器人11个自由度腿部的逆运动问题。当自由足的运动得到全面规定,骨盆中只规定了1个点的路径,骨盆的平移运动能够改善单支撑阶段ZMP的控制。与此同时合成骨盆的旋转运动,进而对自由足姿态实现全面控制。对于NAO机器人步态的研究中,较大程度改善行走过程中ZMP的行为。为人形机器人行走机构的数据参数分析提供支持,进而为机器人及其相关辅助机械设备研究提供帮助。

