采用摩擦补偿的弹药传输机械臂自适应终端滑模控制

姚来鹏， 侯保林， 刘 曦

(南京理工大学 机械工程学院， 南京 210094)

火炮弹药传输机械臂是一类具有参数变化、强非线性的机电系统，其主要功能是将弹丸轴线从接弹位置协调运动到和待发射炮管轴线相平行的位置[1].在弹丸重量的变化以及摩擦扰动等非线性不确定因素的作用下，一般的比例积分微分(PID)控制器无法使弹药传输机械臂获得可靠的控制性能，在工程中不得不采用机械抱闸的方式进行定位，但是这种机械定位的方法会造成较大的冲击磨损，减少弹药传输机械臂的使用寿命，严重降低其整体性能.因此，如何设计弹药传输机械臂的鲁棒控制器是一个亟待解决的问题.

滑模控制是处理具有参数摄动、外部扰动等非线性因素的控制方法之一.该方法具有强鲁棒性、容易工程化的优点，因此得到了广泛的应用[2-4].采用线性切换函数的滑模控制，系统状态与期望之间的误差以指数形式渐近收敛，系统状态只能趋近于期望轨迹，无法抵达期望轨迹.为此，文献[5]提出了终端滑模(TSM)控制，通过在滑模切换函数的构造中引入非线性项，使得在滑模面上的跟踪误差可以在有限时间内收敛到0，解决了传统滑模控制在线性滑模面作用下只能渐近收敛的问题.然而终端滑模控制在奇异控制区域的控制作用将趋于无穷大，不利于实际应用.

文献[6]设计了非奇异终端滑模(NTSM)控制策略，在滑模切换函数构造时避开了控制的奇异问题，同时保留了有限时间收敛特性，并能获得更高的收敛精度.由于NTSM控制方法具有较好的控制性能，所以得到了广泛的应用.文献[7]结合线性滑模和NTSM的优点，设计了混合NTSM控制，使系统收敛变快，和比例积分(PI)控制器相比，增强了永磁同步电动机的鲁棒性.

与线性滑模相比，NTSM在系统状态离平衡点较近时收敛速度较高，但当系统状态远离平衡点时，其收敛时间较长，动态特性变差.为避免控制奇异问题的同时加快系统远离滑模面时的收敛速度，本文采用一种新型非奇异快速终端滑模(NFTSM)控制策略来设计控制律.在实际实现滑模控制的过程中，如何确定滑模控制的切换增益是一个难题.通常系统中的不确定项上界未知，为了确保控制系统具有良好的鲁棒性，切换增益需取足够大的值，但过大的切换增益会造成控制的抖振.为了减弱系统抖振，本文采用自适应控制策略来估计系统的不确定上界，因此无需获知不确定上界的先验知识，有利于实际应用.

本文以某自行火炮的弹药传输机械臂为研究对象，结合自适应控制和NFTSM思想，构造了自适应非奇异快速终端滑模(ANFTSM)控制方法.同时，使用遗传算法对弹药传输机械臂样机运动过程存在的非线性摩擦力矩进行参数识别，并设计了相应的补偿控制.

1 弹药传输机械臂建模

图1(a)所示为某155 mm自行火炮弹药传输机械臂结构图，其工作原理如图1(b)所示.直流电机经减速器带动协调支臂绕耳轴进行旋转运动；弹丸和托弹盘安装在弹药传输机械臂支臂上；平衡机用来平衡负载力矩，以减轻驱动电机工作负荷.

将弹药传输机械臂看作单自由度系统，则弹药传输机械臂动力学方程为[8]

(1)

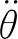
Q=i1η1kTu-TR+TG-Tf+H

(2)

i1为系统的总传动比，η1为减速器传动效率，kT为电动机转矩常数，u为电动机控制电流，TR为平衡机对支臂的力矩，TG为弹丸及弹药传输机械臂支臂的重力矩，Tf为待辨识摩擦力矩，H为参数变化、未建模动态以及外部扰动引起的不确定项.TG取决于支臂的转角：

TG=L1m1gcos(θ+α1)+L2m2gcos(θ+α2)

(3)

式中：L1，L2分别为支臂质心及弹丸质心到弹药传输机械臂旋转中心的距离；m1，m2分别为支臂质量及弹丸质量；α1为支臂质心与旋转中心连线与水平线之间的夹角；g为重力加速度；α2为弹丸质心与旋转中心连线与水平线之间的夹角.

图1 弹药传输机械臂的架构图Fig.1 Architecture of an ammunition transfer manipulator

平衡机由油缸和蓄能器组成，其中油缸压力为

(4)

式中：p0为蓄能器的初始压强；S为油缸活塞面积；V0为气体初始容积；ΔV为气体变化的体积；n为气体的多变指数.则TR为

(5)

式中：l为旋转中心到平衡机的距离；ΔL为活塞运动的距离.

与文献[8]建立的动力学模型的区别在于，本文在文献[8]的基础上进一步细化了弹药传输机械臂的动力学模型，考虑了摩擦力和不确定项对系统的影响，进行弹药传输机械臂的精确定位控制，并且采用电流模式控制电动机运转.而文献[8]建立的模型是用于参数辨识的，采用额定电压控制电动机，接近目标位置时采用机械抱闸的方式定位，并且未考虑摩擦力和不确定项对系统的影响.

2 弹药传输机械臂控制器设计

2.1 ANFTSM控制器设计

(6)

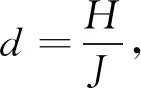
(7)

式中：s为滑模切换函数；β为设计常数，β>0；p和q为正奇数，p>q.控制器设计为

(8)

为了避免传统TSM控制存在的奇异问题， 传统的NTSM切换函数可以设计为

(9)

式中：1

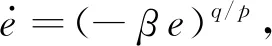
为了改善NTSM切换函数的收敛速度，采用如下新型NFTSM切换函数:

(10)

(11)

式中：k1和k2为设计常数，k1>0,k2>0.对s沿时间求导，并代入式(6)得

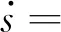
(12)

为了进一步加快系统收敛速度和减弱抖振，本文利用指数趋近律求解控制量，其表达式为

(13)

式中：k为指数趋近系数，k>0,η>0.

综合式(12)和(13)，弹药传输机械臂的控制律可设计为

ks-(D+η)sgn(s)-

(14)

可以看出，式(14)中不含有负指数项，控制量不会产生无穷量，避免了传统TSM的奇异问题.但是，式(14)中含有未知的不确定性上界D，无法直接应用.因此，本文提出一种对干扰上界D进行估计的自适应律，其表达式为

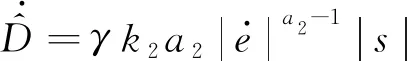
(15)

式中：γ为自适应增益，γ>0.则弹药传输机械臂的自适应非奇异快速终端滑模控制律(ANFTSML)可表示为

(16)

2.2 稳定性证明

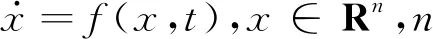
(17)

式中：μ,λ和α为常数，μ>0,λ>0，0<α<1.x(t0)=x0,t0为初始时刻，则系统状态在有限时间内收敛到平衡点.收敛时间为T，则

V(x0)为V(x)的初值.

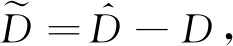
(1) 证明干扰的估计误差有界.取Lyapunov函数

将V1对时间求导数，并代入式(12)得

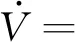
代入式(15)和(16)，化简可得

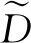
(2) 证明滑模切换函数有限时间收敛.重新选取Lyapunov函数

将V2对时间求导数并代入式(12)得

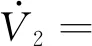
代入式(15)和 (16)，化简可得

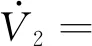
其中：

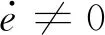
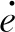
式中：F(·)为高斯超几何函数，其详细信息见文献[12]，证毕.

2.3 摩擦参数辨识

非线性摩擦现象大量出现在机电伺服系统中，是影响系统稳定运行的重要因素之一，其存在非线性时变特性，容易使系统出现较大的误差.为了改善性能，应当采取有效的补偿策略减少摩擦力对系统的影响[13].

对弹药传输机械臂原理样机进行测试发现，工程上常用的Stribeck摩擦理论模型比较符合对实际情况的描述，该模型表达式为[14-15]

Tf=

(18)

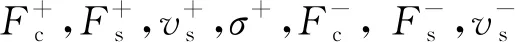
首先，断开弹药传输机械臂和弹药传输机械臂支臂之间的连接，此时系统动力学方程转化为

(19)

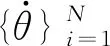
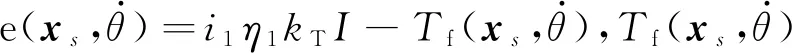
(20)

则求解式(18)中摩擦力的参数问题变为求Je极小值问题.辨识过程如下：

(1) 随机初始化种群P(0)，Xi(i=1,2,…,M)为种群中的个体，t为进化代数，取最大进化代数为T=10 000，种群规模为M=200.

(2) 计算个体的适应度函数

(21)

(3) 判断t是否到达T，若是，则结束算法；否则，转下一步.

(4) 采取保存最优个体的随机采样进行选择操作，组成下代种群P(t).

(5) 以均匀交叉算子pc=0.9进行交叉操作.

(6) 以自适应变异算子pm=0.1-0.099t/T进行变异操作.

(7) 置t+1为t，重复步骤(2)～(6)，输出最终最优解，即为辨识结果.

3 实验验证

为了验证所设计控制算法的有效性，采用实验室弹药传输机械臂原理样机进行定位控制实验研究.不失一般性，为了简化实验装置，采用气弹簧代替平衡机，两级减速器代替弹药传输机械臂减速箱，负载质量块代替弹丸，搭建弹药传输机械臂实验装置，如图2所示.实验台架物理参数如下：p0=0.45 MPa,S=7.85×10-5m2,V0=8.792×10-5m3,n=1.2,m1=2.95 kg,i1=690,L1=0.38 m,L2=0.83 m,α1=α2=0.

弹药传输机械臂系统控制框图如图3所示，实验采用PC机作为上位机，上位机控制算法编程参考图3所示的控制框图.采用LabVIEW软件在上位机中编写，执行电动机选用Maxon公司的RE50直流电机，控制器采用EPOS2(型号70/10)数字位置控制器，控制器通过USB和上位机进行通信交换数据，编码器采用HEDL5540光电编码器，电动机工作在电流模式下.

首先，为了实现摩擦力的补偿控制，采用2.3节的遗传算法对弹药传输机械臂样机进行摩擦力参数辨识.实验结果和辨识结果对比如图4所示，模型参数的辨识结果如表1所示.从图4可以看出，辨识曲线和实验曲线重合度较高，说明求解出的辨识参数准确合理.将辨识结果代入控制律中，进行补偿设计.

图2 弹药传输机械臂原理样机实验装置Fig.2 Experimental setup of the ammunition transfer manipulator prototype model

图3 弹药传输机械臂系统控制框图Fig.3 Control block diagram of the ammunition transfer manipulator system

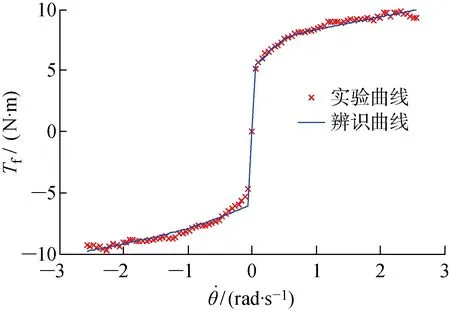
图4 实验结果与辨识结果对比Fig.4 Comparison of experimental data and identified data

表1 Stribeck摩擦模型参数辨识结果

Tab.1 Identified results of the Stribeck friction model parameters

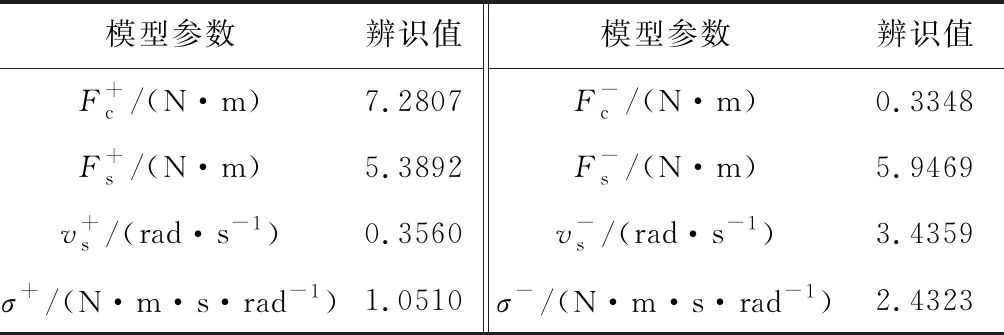
模型参数辨识值模型参数辨识值F+c/(N·m)7.2807F-c/(N·m)0.3348F+s/(N·m)5.3892F-s/(N·m)5.9469v+s/(rad·s-1)0.3560v-s/(rad·s-1)3.4359σ+/(N·m·s·rad-1)1.0510σ-/(N·m·s·rad-1)2.4323

为了更好地解决滑模控制存在的抖振问题，采用饱和函数sat(s)代替sgn(s)，sat(s)的表达式为

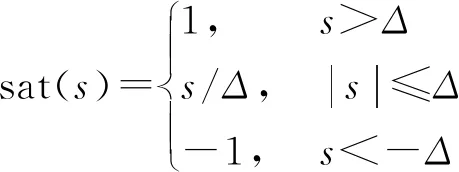
其中：Δ为边界层厚度常数.

控制参数选择为kT=38.5 mN·m/A,i1=690,η1=0.9,a1=2,a2=1.5,k1=220,k2=5,k=50,η=0.1,γ=10,Δ=0.05.实验控制目标为协调支臂由水平位置向下协调30°.实验采用3种不同工况，分别为弹药传输机械臂支臂负载1(m2=0.44 kg)，负载2(m2=0.88 kg)，负载3(m2=1.32 kg).实验结果如图5所示.

由图5(a)和5(b)可以看出，3种不同负载工况下都能够使得弹药传输机械臂快速准确定位到位，定位时间分别为0.63，0.72，0.96 s，说明设计的 ANFTSM 控制算法对负载参数变化和非线性摩擦具有较强的鲁棒性，算法具有更好的动态响应速度.由图5(c)可知，不同负载工况下，控制电流均未产生抖振和奇异问题.由图5(d)可知，不同负载工况下，系统滑模面有限时间收敛到0，验证了定理1的正确性.图5(e)显示了不确定上界自适应估计的收敛情况，不同负载工况下的估计曲线最终都快速收敛到相应的常值，避免了缺少不确定性先验知识的情况下需要取过大的不确定性上界造成控制抖振的问题，更有利于实际工程应用.

图5 不同负载工况的实验结果Fig.5 Experimental results under three different loads

4 结语

弹药传输机械臂系统是一类复杂的非线性动力学系统，其运动过程中存在参数变化、非线性摩擦等干扰因素.为了解决这些因素对弹药传输机械臂系统的影响，本文首先分析了弹药传输机械臂的动力学模型，并采用一种新型NFTSM控制算法设计了相应的位置控制器，避免了传统终端滑模控制的奇异问题和传统NTSM控制收敛慢的问题.同时结合自适应思想，采用自适应估计系统不确定性的上界，无需不确定上界的先验知识，有效减弱了过大的切换增益造成的抖振.针对弹药传输机械臂系统运动过程中存在的非线性摩擦干扰，采用遗传算法对其进行Stribeck摩擦力模型参数辨识，并将得到的参数估计用于弹药传输机械臂的补偿控制.实验结果表明：不同负载工况下，控制器均能实现弹药传输机械臂的快速准确定位，设计的控制器具有良好的鲁棒性，工程实践意义较强.