基于本征正交分解和动态模态分解的尾涡激振现象瞬态过程的模态分析

谢海润， 吴亚东， 欧阳华， 王安正

(上海交通大学 机械与动力工程学院， 上海 200240)

尾涡激振是指处于流场上游物体的尾迹区域内的下游物体受到激励产生强迫振动的一种气动弹性现象，会导致被激励结构的强迫振动.当上游的涡脱落频率接近被激励结构的自然频率时，会产生频率锁定现象，振动的幅值会急剧增大，从而危及结构的完整性与疲劳寿命.频率锁定现象主要是由于下游物体的振动会在一定程度上改变尾迹区域的流动状态，从而使激励力与被激物体之间产生相互作用，使单一的强迫振动现象变成了一种流固耦合的复杂机制.Brika等[1]采用实验方法研究固定的上游圆柱与弹性的下游圆柱之间的流动耦合现象，指出双圆柱的同步振动区域比单圆柱的同步振动区域大，同时指出频率锁定时同步振动发生在较高的折合速度下.Assi[2]分析了两个处于上下游的圆柱之间的尾涡激振现象，对比不同雷诺数下4种直径的圆柱与圆柱相对位置，指出尾涡激振随着下游圆柱偏离中心线而减弱.刘丹青[3]对振荡来流下的单圆柱以及串联双圆柱进行了数值模拟研究，指出当串联双圆柱间距增大时，双圆柱之间的相互作同更加明显，特征是在圆柱间隙形成横流向涡街.

尾涡激振现象中通常包含多个流动特征频率，具有相对复杂的流动特征.而流场模态分解方法是一种能够提取流场主要特征、化繁为简的分析方法.典型的流场模态分析方法有本征正交分解(POD)和动态模态分解(DMD).POD是一种较早提出的模态分解方法，Lumley[4]将其引入到流场分析中，以提取湍流场中的相关性流动结构.POD方法广泛应用于翼型上的湍流分离流动分析[5]、可压缩开放腔体流动分析[6]、基于粒子图像测速法的绕流尾迹动态特性分析[7-8]等.但是POD方法也存在一些不足，为了保证空间模态的正交性，空间模态所对应的时间系数序列往往包含多个频率成分.此外，POD方法按照能量大小进行排序而没有按照动态特性的影响进行排序.针对POD方法的弱点，研究者提出了一些改进的算法，比如采用平衡截断的平衡本征正交方解(BPOD)[9]和结合谱分析方法的谱本征正交分解(SPOD)[10].Schmid[11]最早提出通过动态特性的特征值进行流场模态分析的方法，即DMD方法.Rowley等[12]将Koopman算子与DMD算法相结合，揭示了DMD算法对于非线性系统的意义.DMD方法也存在一些缺点，比如缺少一个单一方法来对特征值的进行排序，即无法确定哪些模态的物理相关性最强，并且DMD模态并非正交模态，导致各个模态之间的内积非零，对于建立降阶模型增加了额外的复杂度.DMD方法广泛应用于横向射流[12]、离心压气机扩压器的流场分析[13]、波包的稳定性分析[14]等.针对DMD方法的弱点，研究者也提出了一些改进的算法，比如稀疏改进DMD，考虑非正交基截断误差的递归RDMD方法[15].两种分解方法的对比研究能够更好地揭示流动物理现象.Noack等[15]针对圆柱绕流的尾迹，比较了这两种模态分解方法以及RDMD方法的优缺点.寇家庆等[16]将两种方法应用于跨声速抖振的模态分析并进行了比较.

本文针对圆柱与叶片的尾涡激振模型，采用Fluent软件对翼型从静止到振荡过程进行了瞬态数值模拟，并通过POD与DMD方法对振荡翼型附近的压力场进行了分解与重构，得到了尾涡激励现象的主要流动特征，并进一步比较了两种模态分析方法的特点.

1 数值计算对象与方法

本文数值分析的对象为圆柱与叶片的尾涡激励模型.由于流动区域中圆柱涡脱落为主要的流动现象，所以采用了文献[17]中的Realizablek-ε模型作为湍流模型.

计算域尺寸与网格细节如图1 所示.计算域左侧为速度入口，右侧为压力出口，上下壁面、圆柱以及叶型为无滑移壁面.圆柱直径为50 mm，翼型为弦长36 mm 的NACA6510翼型，圆柱与翼型之间的距离为112 mm.圆柱中心与翼型型心之间的间距约为圆柱直径的3倍.

流场计算域分为两个子区域，采用结构化网格划分.圆柱贴体网格尺寸按照y+=0.173Re0.9Δy/L进行估算.其中：Re为雷诺数；Δy为第1层网格高度；L为边界层参考尺寸.根据y+=1得到第1层网格高度，建立流场网格.对流场网格的无关性验证分别针对节点数为 38 656、56 153、68 244及116 842 的4套网格进行.圆柱升力系数的计算结果表明，与网格数为 38 656 的网格相比，其余各套网格的计算结果差别均小于1%，因此满足网格无关性要求.但是为了更好地体现翼型附近的流场特征，在计算条件允许的情况下，选择了网格数为 116 842 的网格进行计算.其中计算域2的网格节点数为 45 627，代表了后续模态分解时的空间尺度.

图1 计算域尺寸和网格细节Fig.1 Computational domain size and mesh details

为了实现对翼型振荡的模拟，流体计算中采用了动网格策略.计算域2包含翼型，为实现翼型振荡，将计算域2通过用户自定义函数整体设置为刚体运动，以前期实验测量得到的叶片一阶自然频率(26 Hz)进行简谐振动.该过程中计算域2内部网格相对位置不变， 通过计算域1内网格的变形来实现包含翼型的计算域2的运动.

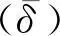
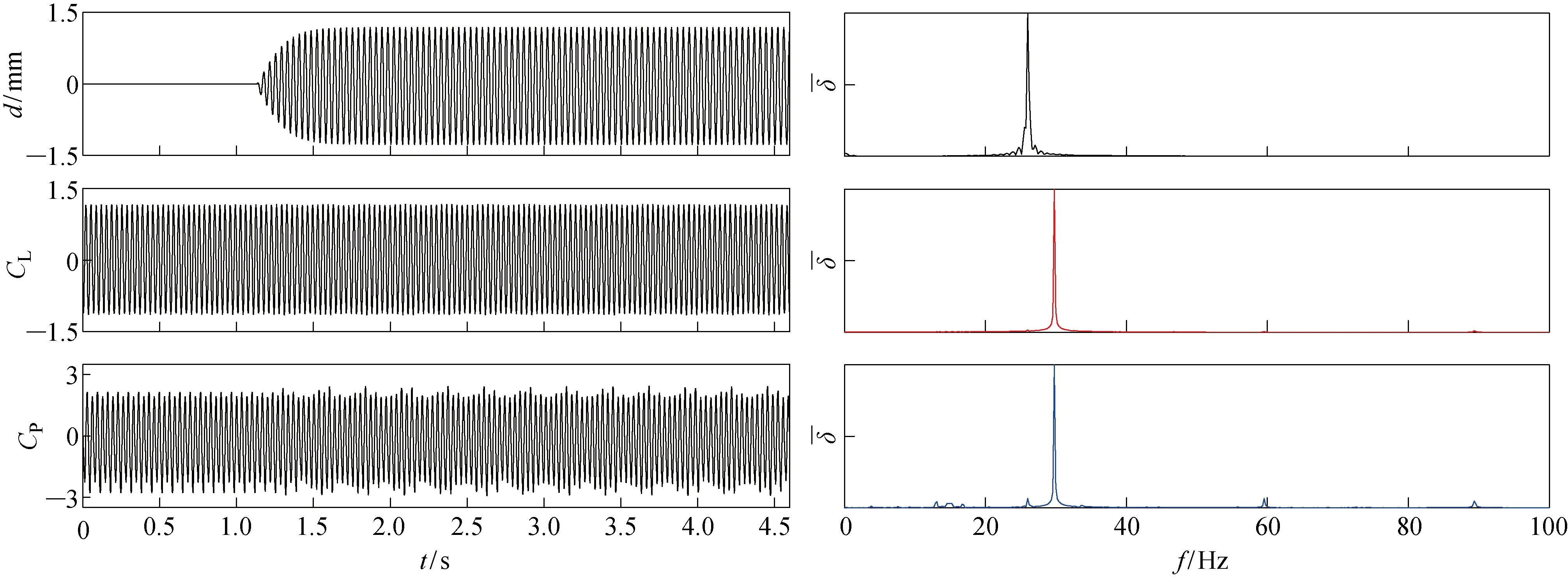
图2 瞬态计算结果的监控点与其对应的频谱Fig.2 Monitoring points of transient calculation and the corresponding spectrum

2 POD与DMD方法

POD和DMD方法具有很多相关性，均可以通过流场各个时间的快照提取主要的流动结构.在流场x∈RN(RN表示实数域)中，对应于时间t的某个变量(速度、压力及涡量等)的向量场u(x,t)可以用M个以相同采样频率提取的流动快照来表示，其中第m个时间点的向量场记作um=u(x,tm)，m=1，2，…，M.

2.1 POD方法

POD方法将流场分解为若干空间正交模态，按照各个模态的能量(特征值)大小进行排序，选择尽量少的基函数或者模态来捕捉流场中的尽量多的能量，有助于建立流场的降阶模型.

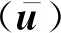
(1)

POD方法中流场的脉动值可以表示为所有正交模态与其对应的时间系数的线性叠加：

(2)

式中：aj(t)为第j阶模态的时间系数；φj(x)为其对应特征向量.将快照POD的数据以矩阵形式表示：

X=

(3)

POD分析的目的是找出最优的基向量来分解流场数据.特征向量φj(x)可以通过最少的模态数量来表示原始的流场.可以通过快照方法求解φj和其对应的特征值λj：

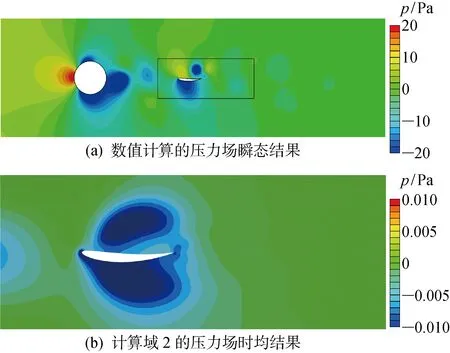
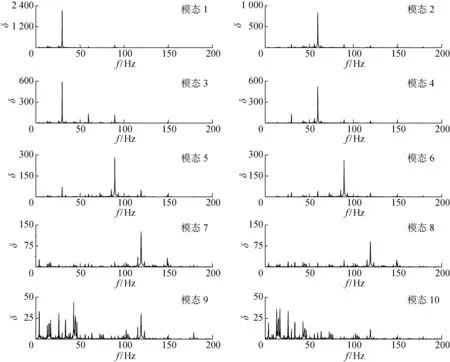
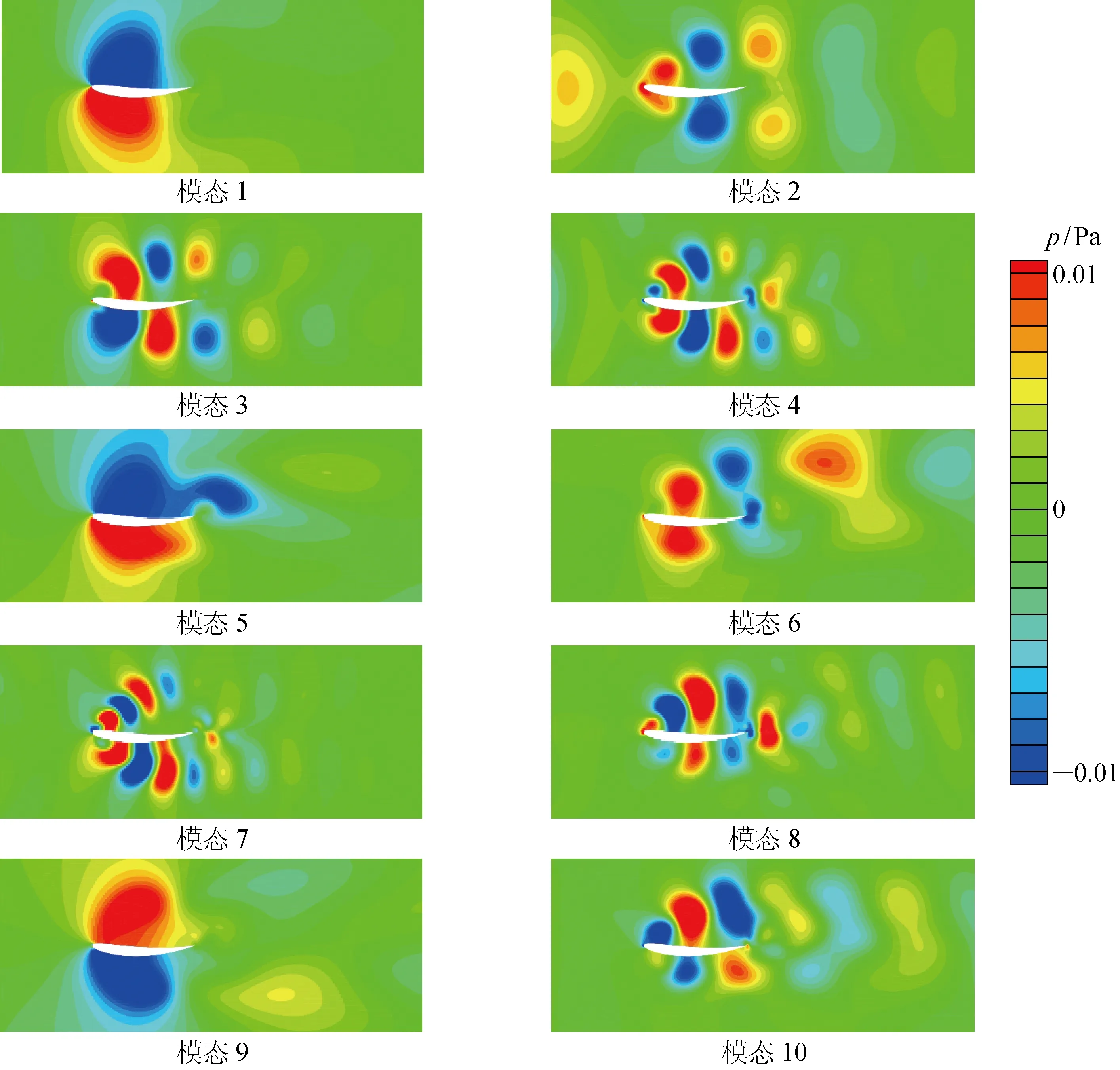
XTXφj=λjφj,φj∈RM,M

(4)

快照方式的POD特征向量可进一步转换为原始POD特征向量：

(5)

式中：ψj为POD模态所对应的流场动能.针对流场瞬态计算的特点，即通常网格尺寸远大于时间步的数量，采用快照方式POD比传统方式POD求解效率更高.快照方式POD所求解的特征矩阵比传统方式POD的特征矩阵具有更小的尺度，因此能够显著减少计算量.

按照特征值的大小进行排序，假设前r阶模态的能量接近流场总体动能：

(6)

则通过前r阶模态重构流场：

(7)

其中时间系数反映了POD模态随时间变化的趋势，能够体现POD模态对应的流动结构在重构流场中的能量占比，时间系数可以表示为

aj(t)=〈v(x,t),ψj(x)〉

(8)

2.2 DMD方法

DMD方法基于一个最佳拟合流场动态特性的线性算子，将流场分解到若干具有单一特征频率和增长/衰减率的模态上.因此DMD可以得到不同频率的流动结构对于流场的贡献.

DMD方法需要两组快照序列作为输入，快照之间有着恒定的时间差.两组快照X、X#通过原始时间序列数据以下列方式构建：

(9)

X∈RN×(M-1)

(10)

X#∈RN×(M-1)

假设X和X#之间存在线性关系，即

X#=AX

(11)

而线性算子A∈RN×N可以通过A=X#X+得到，其中X+是矩阵X的伪逆矩阵.DMD分解的模态和特征值定义为矩阵A的特征向量和特征值.通过以下步骤进行计算.

首先，对矩阵X进行奇异值分解：

X=UΣVT

(12)

得到3个矩阵：U∈CN×N，V∈C(M-1)×(M-1)(C表示虚数域)，Σ∈RN×(M-1)，令

(13)

λj=lgμj/Δt

(14)

λj的实部和虚部分别代表了对应DMD模态的增长/衰减率和频率值.而DMD模态定义为[18]

(15)

用r阶DMD模态对流场进行重构，记作

Ψdiag(exp(λjt))b

(16)

式中：bj(0)为各个模态的初始幅值；Ψ为DMD模态的矩阵形式；b为代表模态幅值的向量.将初始时间步的快照v(x,t1)带入，可以求得各个DMD模态所对应的幅值：

b=Ψ+v(x,t1)

(17)

3 流场的模态分解与结果分析

计算域2共有4 600个快照文件，快照之间的时间步为0.001 s.图3所示为计算域压力场某一时刻的瞬态结果以及的计算域2内压力场的时均结果，图中p为压力.可以看出，上游圆柱后已经形成了成对出现的涡街，在计算所处的亚临界区域内，涡脱落的形态与文献[19]中相似工况下的结果一致.圆柱尾迹产生的涡团会沿着圆柱中线附近向下游发展，上下交替产生的涡团会持续撞击在翼型上，从而给翼型施加了一个持续的脉动力.翼型进一步将涡团打散，使其失去主要涡街的一些特征.而时均压力场则显示在时间平均的条件下，翼型的上方与下方为一个低压区域，且吸力面与压力面的压力存在差异，体现了翼型对于压力分布的非对称性的影响.

图3 流场的快照与计算域2的时均结果Fig.3 Snapshot of flowfield and time-averaged result of Domain 2

图4 前50阶模态的残差Fig.4 Residuals of the first 50 order modes

3.1 流场的POD分解

POD分解针对计算域2进行.分解得到的模态根据各阶模态的特征值大小进行排序.定义前r阶模态所重构的流场的残差为

(18)

图4所示为前50阶模态的残差.可以看出，前10阶模态的残差已经低至10-4，因此可以认为前10阶模态可以反映流场的主要能量.

图5所示为以压力云图显示的前10阶POD模态.可以看出，模态1和3以翼型为分界，上下呈现相反的压力.模态2和4则呈现出被翼型一分为二的涡团.模态5、6和模态7、8与低阶模态呈现高度的相似性，涡团更加密集.模态9和10 则较为奇异，体现了较复杂的流动形态.

图6所示为前10阶POD模态所对应的时间系数的频谱，图中δ为幅值.在针对标准的圆柱绕流涡脱落的流场POD模态分解中，POD模态通常会呈现出以相同幅值和频率成对出现[15].成对出现的POD模态表示同一个频率的涡脱落的现象，本质上反映了同一个涡脱落的模式在空间上的发展.由图6可以看出，模态1和3具有主要的频率成分，均包含有30 Hz的涡脱落频率和26 Hz的翼型震荡频率，其中翼型震荡频率幅值较低.模态2、4，模态5、6和模态7、8可以理解为模态1、3的倍频.模态9、10的频谱与前8阶模态不同，包含了更多的频率成分.POD以较少的模态数反映流场的流动特征，对于流场的重构与降解模型的建立具有很大的作用.POD以能量(特征值)进行排序的方式，能够在一定程度上反映各个模态的流动结构对于流场的贡献.但该排序方式会忽视各个模态所对应的流动现象，各个模态均为具有多个频率成分，对于脉动流场的物理意义不够明确.

图5 以压力云图显示的前10阶POD模态Fig.5 The first 10 POD modes displayed by pressure contour

图6 前10阶POD模态时间系数的频谱Fig.6 Spectrum of time coefficient of the first 10 POD modes

3.2 流场的DMD分解

DMD分解的零阶零频模态代表了平均流场.图7所示为DMD模态的特征值分布以及前10阶模态所对应的频率与幅值，图中下标real，imag分别表示实部及虚部.可以看出，几乎所有的特征值都分布于单位圆上，说明流场中主要流动结构均处于稳定的状态，与流场设置的边界条件符合.其中较大的点是按照2.2节中模态幅值定义进行排序的前10阶模态.将前10阶模态所对应的频率与归一化的幅值以柱状图表示，可见DMD第1阶模态的幅值与平均流场的幅值较为接近.第1阶模态对应涡脱落频率30 Hz，而模态2，3，4，7对应1阶模态的倍频，但模态幅值随模态数增加而迅速下降.第9阶模态对应翼型振荡频率26 Hz，其模态幅值相对较低.

DMD模态以共轭形式成对出现，每一对共轭的特征值可以视为一个DMD模态.图8所示为前10阶的DMD模态.可以看出，DMD的第1阶模态和POD的第1阶模态非常相似，而其对应的频率为涡脱落频率30 Hz.而模态2、3、4以及7则可视为模态1的倍频.代表翼型振荡频率26 Hz的第9阶模态与第1阶模态在压力分布的形态上具有高度相似性.

图7 DMD模态的特征值分布以及前10阶模态所对应的频率与幅值Fig.7 Distribution of eigenvalues and corresponding frequencies and amplitudes of the first 10 DMD modes

图8 以压力云图显示的前10阶DMD模态Fig.8 The first 10 DMD modes displayed by pressure contour

4 POD与DMD对比

为了将POD和DMD的结果进行对比，将反映流场主要特征频率的模态进行比较.POD是将流场按照空间和时间进行分解，得到POD模态与其对应的时间系数.各个POD模态的幅值反应了瞬时流场的结构，时间系数则表示对应模态随着时间变化的情况.而DMD是将流场按照空间和频率进行分解，得到的DMD模态都有着对应的增长/衰减率和频率，进一步可以建立每个模态所对应的时间系数.图9所示为第1、2和9阶POD模态以及DMD模态的时间系数.参考图6中POD模态的时间系数频谱，第1阶模态中主要包含30 Hz和26 Hz的频率成分，其分别对应于圆柱的涡脱落频率和翼型的振荡频率，而涡脱落频率幅值相对较高.第2阶模态中主要频率成分为第1阶模态的倍频.第9阶模态的频谱中具有较多的频率尖峰，反映其包含相对复杂的频率成分，但是其中30 Hz处无尖峰，说明该模态与涡脱落现象的相关性较低.从时间系数可以看出：第1、2阶POD模态的时间系数在t<1 s时保持30 Hz稳定振荡；t>1 s时，随着26 Hz的翼型振荡频率的进入，形成了较为明显的节拍.第9阶POD模态的时间系数更明显地反映新的频率成分进入稳定流场的过程，1 s前后的振荡形态有着明显的差异.DMD模态对应着单一的频率成分，第1阶DMD模态对应30 Hz的涡脱落频率，第3阶模态对应60 Hz的涡脱落频率的二倍频，第9阶模态对应了26 Hz的翼型震荡频率.可以从时间系数中看出，第1阶和第2阶模态的幅值在整个计算周期中基本保持稳定，而第9阶模态的幅值则逐渐增大，表明翼型振荡对流场的影响是从无到有，从小到大的.对比POD模态和DMD模态可以看出，POD模态的时间系数明显反映出翼型振荡前后流场所发生的变化；而DMD模态的时间系数中则没有明显的分界线.但DMD模态反映出各个具有物理含义的频率成分的变化规律，有利于针对性地研究流场中的特定流动结构.

基于前文得到的前10阶POD模态与DMD模态对流场进行重构，基本能较好地反映流场特征.但进一步的误差分析显示，POD模态和DMD模态重构的流场具有差异性.图10所示为用前10阶POD和DMD模态重构流场压力的方均根误差(RMSE)的瞬时结果.可以看出，POD模态重构的流场误差基本处于一个稳定水平，但是图中t<1 s时的脉动幅值小于t>1 s的脉动.而DMD模态重构的流场误差起初较小，然后随着时间增加逐渐增大，t>1 s时流场的误差增加到一个较大的值并以较大的振幅振荡.比较两者的差异，可以看出，t<0.5 s时，DMD误差小于POD误差，但是t继续增大时，POD误差小于DMD误差.

图10 用前10阶POD和DMD模态重构流场的方均根误差的瞬时结果Fig.10 RMSE of reconstructed flow field with the first 10 POD and DMD modes

图11 前10阶POD和DMD模态重构流场方均根误差的时均云图Fig.11 Time-averaged RMSE contour of reconstructed flowfield with the first 10 POD and DMD modes

图11所示为用前10阶POD和DMD模态重构流场的RMSE归一化后的时均云图.两者采用相同的标尺表示.可以看出，时均结果中POD的误差最大值显著小于DMD误差.而两者误差较大的区域均处于翼型前缘上下的部分.这是由于该区域流动现象较为复杂，存在着多种其他频率成分的流动结构.DMD模态分解的误差主要分布区域与DMD模态1、5、9误差区域较为重合，说明误差可能主要来源于相关的频率成分.

通过对比可以看出，POD模态分解在处理截断误差时比DMD模态的整体表现更为优秀.主要原因为POD模态分解时以正交形式构建的基向量，因此较少的模态数即可较好地表示整体流场的脉动.尽管DMD的最大误差大于POD分解的误差，但在流场稳定脉动的过程中，DMD分解误差较小.

5 结论

本文通过Fluent软件针对翼型由静止到振荡过程的瞬态数值模拟，提取了振荡翼型周围的流场，通过POD和DMD两种模态分解方法，对流场进行了分解与重构，捕捉到尾涡激振现象的主要流动特征，得到上游的涡脱落频率与翼型的振荡频率以及其对应的模态特征.基于尾涡脱落现象与流场瞬态变化的特点，对两种模态分解方法进行了对比，主要结论有：

(1) POD模态分解是将流场按照空间与时间的方式进行分解，其中各个空间模态是正交的.POD模态按照能量(特征值)进行排序，较少的POD模态数即可将流场的残差快速降低.POD模态的时间系数可能包含多个频率成分，不利于研究流场中的主要脉动结构，但可以较为清晰地在时间上显示变化的关键节点.

(2) DMD模态分解是将流场按照空间和频率的方式进行分解，其中各个空间模态并非正交.DMD模态的排序不具有单一的正确方式，因此在物理上客观地确定模态的最相关性比较困难.DMD模态对应着单一的频率成分，可以提取特定频率的动态流动结构.模态的增长/衰减率可以反映频率成分的变化情况，但难以表示关键的时间节点.

(3) 在本文的算例中，POD模态分解的最大误差小于DMD模态分解的误差，但DMD分解在稳定脉动的流场中可以得到更小的误差.

POD和DMD两种模态分解方法具有各自的优点和缺点.在流场稳定脉动时可以采取DMD方法，而伴随其他随时间变化的流动现象时，需要结合POD方法或其他方法.