基于模型预测控制的汽车主动避障系统
杨丰萍,谢梦莎,彭理群,郑文奇,刘 锋
(华东交通大学电气与自动化学院,江西 南昌330013)
智能汽车主动避障[1]过程是指汽车根据车辆相关传感器提供的信息,动态规划出一条能绕过障碍物且符合汽车动力学性能要求的避障路径,并能自主控制汽车按照该路径安全稳定地行驶。 智能汽车主动避撞系统是智能交通和主动安全技术的一个重要方面,能辅助驾驶人在紧急状况下采取正确的避碰决策和控制策略,从而减少交通事故的发生,进而提高道路交通系统的安全性。
整个系统涉及到环境感知、路径规划和路径跟随控制三个关键技术[2]。 常用的路径规划算法有人工势场法[3]、栅格法、蚁群算法和混沌粒子群算法[4-5]等。 其中,人工势场法较于其他算法,具有算法简洁、计算速度快、实时性强等优点而被广泛使用。 但传统的人工势场法存在局部极小值的问题[6],导致路径规划时不能到达目标点。 考虑到智能汽车行驶过程中的动态环境,选取改进人工势场法[7]进行路径规划;常用的跟踪控制方法有预瞄跟踪控制[8]、模糊控制、改进追踪控制、滑模控制、模型预测控制等,模型预测控制的优点[9-10]是能在控制过程中增加多种约束,如车辆运动学约束、动力学约束,因此选择模型预测控制进行路径跟踪。
综合考虑动态的道路交通环境和路径规划实时性,通过对传统人工势场法的改进,建立道路边界斥力势场、动态障碍物斥力势场和引力势场,规划避障路径。 通过对模型预测控制模型的建立,控制车辆按照规划的路径行驶,利用Carsim/Matlab 联合仿真验证路径规划与跟踪效果,以保证智能汽车的主动避障。
1 主动避障系统框架
汽车主动避障系统采用分层控制结构,由环境感知、危险态势评估、路径决策和控制执行等4 层构成。如图1 所示。 环境感知层根据雷达、机器视觉、车载传感器等获取车外环境信息和和自车运动状态信息。 具体如车道信息和周围其他车辆信息,自车的状态信息包括自车当前位置、方向盘转角、速度、油门开度等;危险态势评估层依据前两层提供的信息利用安全距离模型[11]对行车安全进行判断;路径决策层根据已有的信息对汽车进行无碰撞路径规划;控制执行层对汽车的转向、驱动及制动结构进行操纵,使车辆跟踪规划的避障路径。
2 局部路径规划
2.1 道路边界斥力势场模型
将道路边界线视为障碍物,本文仅考虑双向单车道,道路边界线对道路中的车辆产生斥力,道路边界斥力势场的大小将由汽车与道路边界的距离决定,汽车越靠近边界线受到的斥力越大,借鉴人工势场模型公式,道路边界斥力势场函数表达式为
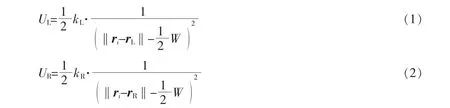
式中:UL,UR分别为道路左右边界线的斥力势场;kL,kR分别为道路左右边界斥力势场的比例系数,根据一般人的驾驶习惯,使汽车在无需避障的情况下能沿着右车道的中心线行驶,定义kL/kR=9;ri为车辆质心的位置向量;rL,rR分别为道路两边界与质心位置相交的位置向量;‖ri-rL‖,‖ri-rR‖为车辆质心与道路两边界之间的距离,W 为车宽。
道路边界斥力由对道路边界斥力势场函数进行梯度运算得到,受力模型如图2 所示。
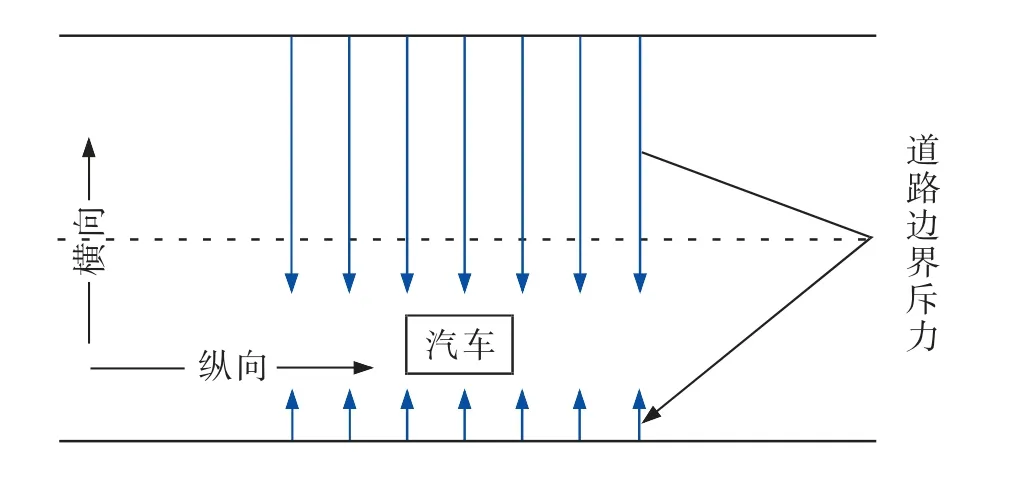
图2 道路边界斥力示意图Fig.2 Road boundary repulsion diagram
2.2 动态障碍物斥力势场模型
在传统的人工势场模型中,当斥力与引力的合力为零时,而汽车此时又未到达目标点,会陷入局部最优;当汽车在目标点附近,而斥力与引力的合力不等于零,此时会出现连续抖动目标不可达的现象,因此通过在斥力势场函数中加入汽车与目标点的相对距离的方法来消除局部极小值点[7]。
改进后的斥力场函数为

式中:η 为改进后斥力场比例系数;ρ(X,X0)表示位置点X 与障碍物之间的最小距离;ρ0表示障碍物的影响范围;ρgn为汽车与目标点的距离,n 的值取2。
在现实的行驶环境中,遇到的障碍物可分为两大类,一类是静态障碍物,一类的动态的障碍物。 避障过程中动态障碍物也以一定的速度行驶。 为了使改进的人工势场法能适用于动态环境中的路径规划,引入速度斥力势场,势场函数为

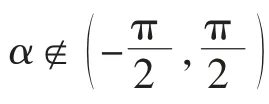
速度势场斥力为

2.3 引力势场
引力势场由汽车和目标路径之间的距离决定,引力势场函数Uatt(X)定义为

式中: Uatt为势能场中点X 处的引力场;k 为引力场增益;Xg为目标点(车道中线上)的位置。 ρ(X,Xg)为目标点与汽车两位置之间的欧氏距离。 汽车受到的引力Fatt为该点势场能的负梯度。
2.4 避撞路径求解
汽车受到合力场的作用,当受力平衡时势场和为零

对势场函数式(6)进行梯度运算得到受力方程

式(8)是非线性方程,用Jacobi 迭代法求解。 汽车的运动可分为纵向运动和侧向运动,如图2 中的示意,通过求解汽车在纵向上的受力平衡方程可得到汽车避障时的具体位置坐标,最后经过曲线拟合得到避障路径。
3 模型预测控制器
路径跟随过程中运用的模型预测控制算法过程如图3 所示。 其中虚线框部分是该控制器的主要成分,由线性误差模型、系统约束以及目标函数组成。线性误差方程是描述轨迹跟踪系统的一般表达式。而系统约束主要有车辆机械结构约束、车辆稳定性约束等。 目标函数的选择应该缩小轨迹跟踪时的输出值和目标值的误差。
3.1 车辆运动学模型
在地面固定坐标系OXY 下, 车辆运动学模型公式[13]为

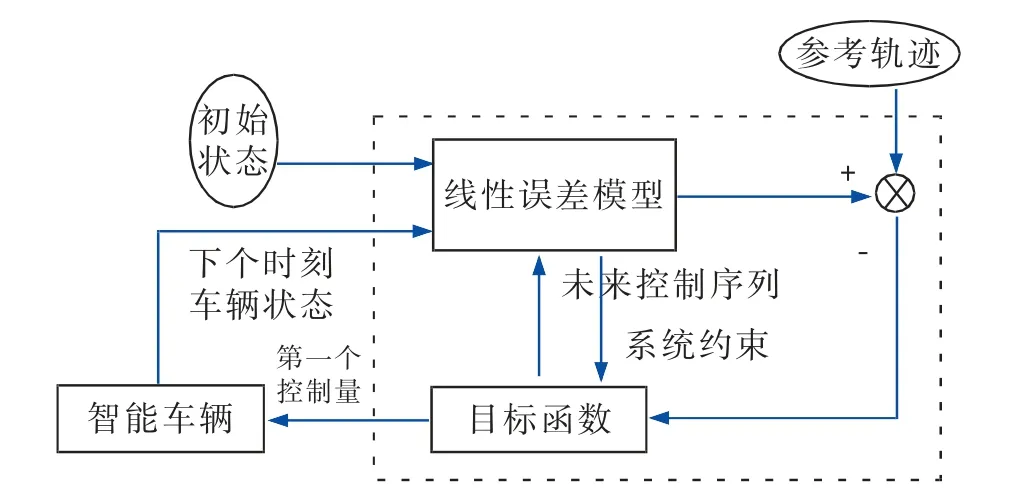
图3 基于模型预测控制的轨迹跟踪控制器Fig.3 Trajectory tracking controller based on model predictive control
式中:(x,y) 为车辆后轴中心的坐标;φ 为车辆航向角;δ 为车辆前轮偏角(车辆前轴中心速度与车辆后轴中心速度的夹角);v 为车辆后轴中心速度;l 为轴距。
由式(9)可知,系统能视为一个输入u(v,δ),状态量为χ(x,y,φ)的控制系统,用z 表示参考量,该模型可进一步表示为更一般的形式

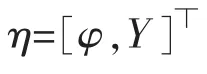

3.2 目标函数设计
目标函数的选择应该尽量缩小轨迹跟踪时的输出值和目标值的误差,用控制增量替代控制量作为状态量,采用的目标函数为[13]
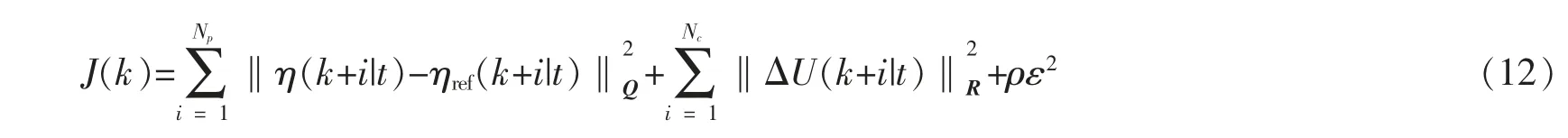
式中:Q,R 分别为输出量和控制增量的权重矩阵;ΔU(t)为控制增量;Np为预测时域;Nc为控制时域;ρ 为权重系数;ε 为松弛因子。 ηref=[φref,Yref] 为参考输出变量,Yref由上节中的改进人工势场法规划的路径得出,φref航向角可由车辆运动学约束和阿克曼转向定理联合求解出[14]。
为求解式(12)中的目标函数,做如下转换

得到新的状态空间表达式

3.3 约束条件设计
车辆在行驶过程中会受到车辆相关机械结构约束、车辆稳定性约束以及周边环境的约束的影响,因此在设计目标函数时,需要满足的相关约束如下:
控制量约束表达形式

控制增量量约束表达形式

输出约束表达形式

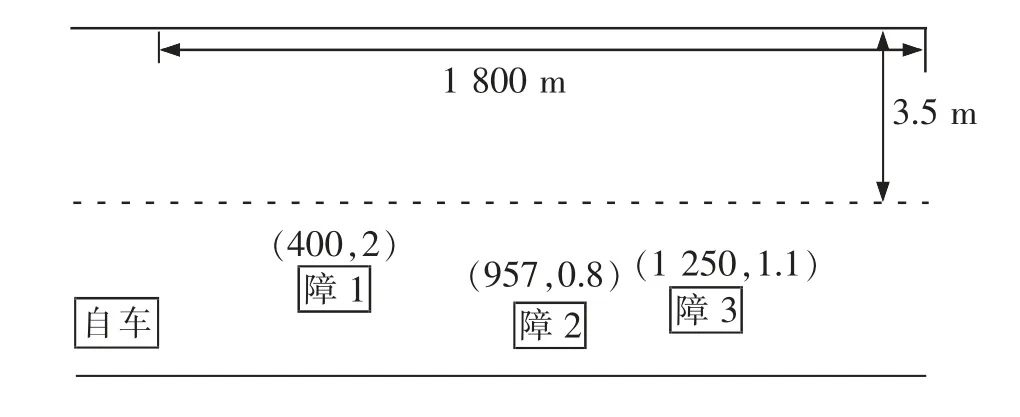
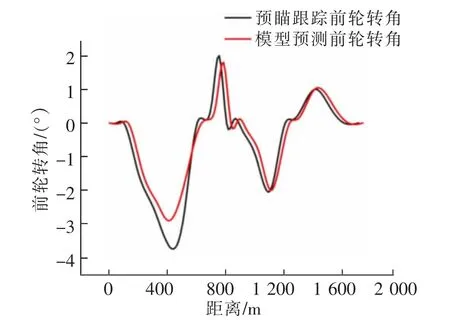
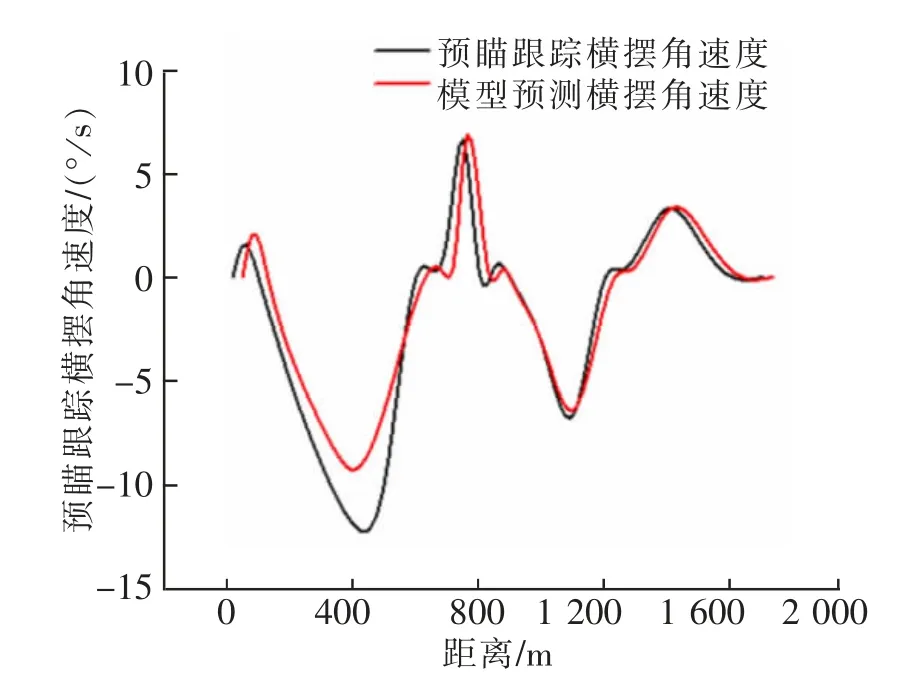
除上述基本约束条件外,为了使跟踪过程更加平稳舒适,考虑车辆动力学相关约束,将车辆前轮偏角约束和横向加速度约束设置为,车辆极限前轮偏角约束:-25°< δ <25°;质心侧偏角约束: -11°< β <11°;横向加速度约束:aymin-ε 结合约束条件与目标函数,将每个控制周期内的优化转化为二次规划问题 求解带约束的目标函数式(18)后,会得到控制输入增量 结合控制输入增量和初始控制序列中第一个元素计算下一周期的控制量 如此重复上述求解过程,完成对车辆轨迹的跟踪。 为使仿真更贴合真实的驾驶环境,设置两个动态障碍物和一个静态障碍物,两个动态障碍物的初始位置分别为(957,0.7),(1 250,1.1);动态障碍物的速度均为10 m/s,动态障碍物靠近和远离汽车的方向如图所示;自车的行驶速度为25 m/s;静态障碍物的位置为(400,2),相关位置示意图如图4 所示;在matlab 环境中进行模拟计算,得到动态避障路径,在Carsim 中建立准确的整车高精度模型,车辆基本参数如表1 所示。在Simulink 中搭建路径跟踪控制器,将计算出的避障路径导入控制模型, 得到路径跟踪的行驶图、跟踪行驶时的侧向位移误差曲线、前轮偏角曲线、侧向加速度曲线、横摆角速度曲线。 最后将预瞄跟随控制器与模型预测控制器得到的结果进行对比。 分别利用驾驶员预瞄控制模型和模型预测控制模型对路径进行跟踪,图5 至图8 分别为两种跟踪控制模型对比得出的侧向位移误差、前轮偏角、侧向加速度和横摆角速度图。 图4 位置示意图Fig.4 Location map 表1 车辆动力学模型基本参数Tab.1 Basic parameters of vehicle dynamics model 图5 侧向位移误差对比图Fig.5 Comparison chart of lateral displacement error 图6 前轮偏角对比曲线Fig.6 Front wheel declination curve 图7 侧向加速度对比曲线Fig.7 Lateral acceleration contrast curve 图8 横摆角速度对比曲线Fig.8 Yaw angle velocity comparison curve 表2 对比结果Tab.2 The comparison results 由图5~图8 与表2 可得,利用模型预测控制得出的侧向位移误差±0.13 m<0.15 m,前轮偏角范围±3°<3°,避障过程中最大侧向加速度0.3 g<0.4 g,最大横摆角速度10°/s<15°/s。 由此可以看出模型预测跟踪控制中的各项数据都优于驾驶员预瞄跟随控制中对应的数据,且满足各项约束条件。 说明汽车在避障过程中利用模型预测控制器来跟踪路径具有有更好的稳定性和舒适性。 本文搭建了智能汽车主动避障系统,建立了以道路边界斥力势场、动态障碍物斥力势场和引力势场核心的路径规划模块,利用模型预测控制器实现对规划路径的跟踪,仿真验证的结果表明,建立的模型预测控制优于驾驶员预瞄控制,对路径具有更好的跟踪效果、提高了精度,保证汽车在避障过程中具有更好的稳定性和舒适性。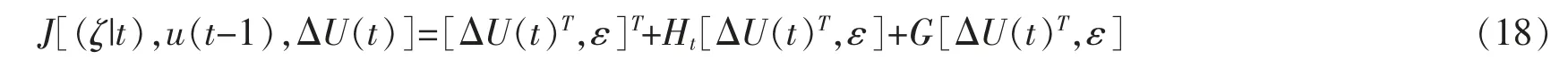


4 模拟仿真




5 结束语

