基于GMS和GS_LMEDS的图像匹配算法

纪栋梁，张国伟，云伟俊，疏雅丽，王博

（1.上海电力大学自动化工程学院，上海200082；2.上海市闵行区高新技术产业化促进中心，上海201100）

针对GMS算法在特征点检测较少时存在误匹配的问题，结合高斯滤波和LMEDS，提出一种基于GMS和GS_LMEDS的特征匹配算法。该法首先对图像预处理，进行高斯滤波，再使用ORB算法提取特征点和特征描述子，使用Brute-Hamming进行粗匹配，最后使用GMS做初次精匹配以及LMEDS做二次精匹配。实验成果表明：相比于其他二次精匹配算法，该算法能有效去除错误的匹配点，准确匹配率普遍更高。

图像匹配；GMS；误匹配；准确匹配率

0 引言

图像匹配主要是检测两幅或多幅图像的相似性或一致性，在目标识别、三维重建等方面都起着重要作用。常用方法主要分为基于灰度信息[1]和基于特征[2]，目前大多算法都采用基于特征的方法，一般完整的基于特征匹配的方法主要包括特征提取、特征匹配和剔除误匹配三个过程。匹配效果主要在于特征提取准确度以及速度等性能，例如待匹配图像在旋转、缩放、光照等方面的差异都会影响匹配效果[3-6]。

目前，图像匹配方法有多种，其中常用的有SIFT[7]、SURF[8]和ORB[9]等。SIFT（Scale Invariant Feature Transform）在图像尺度变换、旋转变换及亮度变化方面有高稳定性，且对噪声污染、视角和仿射变换有较强的鲁棒性，劣势主要在于运算成本高。SURF（Speed Up Robust Feature）是在SIFT上改进而来，在特征点和特征描述向量方面进行完善，运算成本得到大幅降低，并且具有很强的鲁棒性。ORB（Oriented FAST and Rotated BRIEF）算法结合FAST[10]和BRIEF[11]算法，具有尺度和旋转不变性，匹配的质量高，最大优点是速度快。但ORB特征匹配时精度较低，需进行进一步精匹配。GMS[12]（Grid-based Motion Statistics，GMS）算法由Bian等提出，该算法基于网格运动统计，将运动平滑度作为统计量，具有计算快、鲁棒性强的特点，但也依旧存在误匹配点。最小中值法[13]（Least Median of Squares，LMEDS）可以看成是最小二乘法的改进，计算机视觉的输入数据是图像，一般都包含噪声，此时最小二乘法往往无法正确拟合数据，而LMEDS可以更好实现拟合，排除outlier数据，但该算法对高斯噪声敏感。

针对上述分析，本文提出一种基于GMS和GS_LMEDS的图像匹配算法，目的在于进一步提高准确匹配率。首先对图像高斯滤波，再利用ORB提取特征点和描述子，然后通过Brute-Hamming进行粗匹配，最后使用GMS初次精匹配，最小中值法做二次精匹配。实验成果表明，相比于其他二次匹配算法，本文算法具有更高的准确匹配率。

1 ORB算法

1.1 特征检测与提取

特征点即为图像中比较显著的点，例如边界点、亮区域暗点、暗区域亮点，等等。ORB使用FAST来获得特征点，该法步骤如下：首先选取一个像素点P，设定一个合适阈值t，当两点之间的灰度值差的绝对值大于t时，认为这两点不同。然后在P点周围选择一个半径r的圆，圆上所有的像素点便是评价P点是否为特征点的依据。图1中r=3，因此需要考虑P点周围的16个像素。如果圆周上有连续8个点满足灰度值差绝对值大于t，则将P设为特征点。为了减少计算成本，FAST算法中仅将P与圆中的4个等距像素相比，例如选取1、5、9、13位置上的灰度值，如果P为特征点，那这四个位置上必有3个或4个满足条件。

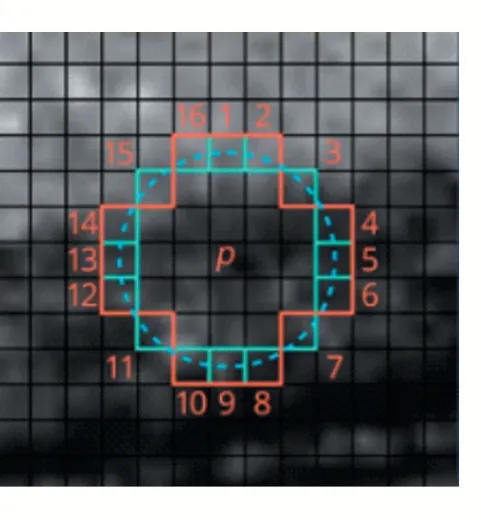
图1 特征点检测

为了获得旋转不变性，ORB用矩法确定FAST特征点方向。由矩计算出特征点周围r半径区域质心，特征点坐标到质心形成一个向量作其方向。矩定义如下：式中I(x,y)为图像灰度表达式。该矩的质心为：

假设特征点坐标为原点，则向量角度即为其方向。计算公式如下：

FAST计算速度快，但其提取的特征点无尺度不变性，若图像缩放则无法匹配相应特征点。为改进这一点，需使用图片的尺度金字塔，单图像的多尺度表示法由原始图像的各分辨率版本组成，在各尺度计算FAST特征点。具体做法为设置比例因子scaleFactor（一般取1.2）和金字塔的层数nlevels（一般取8），按照scaleFactor值将原图缩小成nlevels幅图像，缩放后图像为：

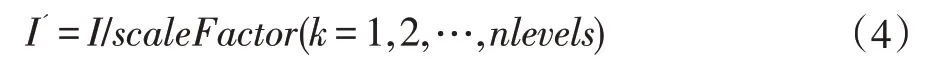
nlevels幅不同比例图像的特征点即为这幅图像的oFAST特征点。

1.2 特征描述子

rBRIEF由BRIEF加旋转因子改进而来，具体步骤如下：在特征点P的邻域内，选n对点pi、qi（i=1,2,…,n），然后比较每对的灰度值，如果I(pi)>I(qi)，则生成二进制串中的1，否则为0。所有点对比较所得结果合在一起，得到长度为n（一般取256）的二进制串。

BRIEF描述子在选取点对时是以当前特征点为原点，以水平方向为x轴，以垂直方向为y轴建立坐标系。当图片发生旋转时，坐标系不变，若还使用同样的取点模式得到的描述子就不一样。在计算描述子时，rBRIEF将特征点设置为原点，特征点和形心连线做为x轴建立坐标系，这样遇到图像旋转，ORB选取点对的坐标系是固定的，即满足旋转一致性。

1.3 特征匹配

ORB具有一个二进制串向量形式的特征描述子，使用汉明距离计算各特征描述子之间不同位值的数量，将其中距离最小的特征点作为匹配点。

2 GMS算法

GMS是一种基于统计的匹配算法，其核心内容如下：由于运动具有的平滑性，使得匹配出现一对多的情况，即匹配到的特征点周围也存在多个符合条件的匹配点，统计这些都符合条件的匹配点数，依此为依据来判断该匹配正确与否。

假设图像PL中有m个特征点集合{α1,α,…,αm}，图像PR中有n个特征点集合{β1,β2,…,βn}。PL和PR所有的特征匹配集合{γ1,γ2,…,γk}，其中γi=(αi,βi)表示一对特征点匹配对。当匹配正确时，则有：

其中：1表示原来正确匹配的特征点。因为匹配具有足够小的面积以及相对独立分布的点对，可将其二项分布表示为：

其中：n表示匹配点对的数量，K表示与γi所在网格区域相邻不相交的网格数目，pt表示准确匹配率，pf表示错误匹配率。根据式（6）可以得出Si标准差与均值：

根据Si的标准差和均值设定用于判断匹配的邻域特征点支持量阈值：

其中：mf一般极小，而Sf和α都较大，可以将mf省略不计。

对于一个网格区分匹配的邻域特征点支持量阈值：

根据式（10），保留待配准网格中邻域特征点支持量大于τi的粗匹配点对，剔除小于该值的点对，到此GMS便完成了对粗匹配对的筛选。

3 GS_LMEDS算法

由于GMS进行特征匹配后仍有错误匹配，所以本文使用LMEDS算法对GMS后所得的匹配特征点对再一次进行误匹配剔除，该算法从样本中随机抽出N个子集，使用最小二乘法，计算各子集的估计参数和偏差，得到各子集中居中的那个偏差（即Med），最后选N个样本子集中Med最小的所对应参数作为拟合参数。该法对高斯噪声敏感，所以在特征匹配前先对图像进行高斯滤波，提高算法的鲁棒性，并且实验中发现使用高斯滤波可以得到更高的匹配准确率。

4 实验与分析

为了体现本文算法在匹配准确度与运行速度上的性能，将其与ORB+GMS+RANSAC、SIFT+GMS+RANSAC、SURF+GMS+RANSAC比较，测试平台为个人笔记本：操作系统为Ubuntu 16.04，处理器为Intel Core i7-9750H CPU@2.6GHz，内存16GB。运行环境是系统终端，调用OpenCV 4.1.1，程序采用C++编写，测试数据集为Oxford标准仿射变换图集。

通过准确匹配率（Correct Matching Rate，CMR）和运行时间对算法评价，其中CMR定义为：

其中：内点数为算法最终保留的匹配对数，重复特征点数指的是两幅图像的单应矩阵计算所得，假设在图像a中选择m个特征点，图像b中选取n个特征点，先将a中m个特征点集分别乘以两图像的单应矩阵H，生成新的点集m1。将新点集经过图像b范围约束筛选后，得到剩余点集m2；将图像b的n个特征点分别乘以H-1，生成新点集n1。该点集经过图像a范围约束筛选后得到剩余点集n2；然后根据重复率评估公式：

其中：分子dist(m2,n1)为两个点集的点之间的欧氏距离，如果其阈值小于设定值，则该点就是一个重复点。最后，两图像的重复特征点数由选取的特征点数乘以重复率所得。

图2展现了本文算法与其他三种二次精匹配算法在Oxford图集的4个子数据集的CMR对比。数据集包含了光照敏感对比（Leuven）、模糊度对比（Bike）、视角转变和尺寸缩放（Bark）、图像压缩（Ubc）这四类配准测试图像。由图2的4幅图像可以看出本文算法在视角转变和尺寸缩放方面比其他算法更加出色，匹配准确率比ORB+GMS+RANSAC算法平均高8%。除了在模糊度对比方面与其相差不多，在光照和压缩方面本文算法的匹配准确率比ORB+GMS+RANSAC要高3%左右。此外，由图可以明显看出选用ORB算法比SIFT和SURF可以获得更多的匹配对及更高的准确匹配率。

图3（b）～（e）展示了以Oxford图集中Bark子图集为例，应用本文与其他三种算法进行图像配准的效果。Oxford图集中配准最难的便是Bark子图集，该图集包含了极大角度的视角变换和尺寸缩放，表1展示了各算法在该图集的结果。由表1可以看到本文算法在匹配准确率上明显优于其他算法，CMR比其他三个算法分别高了8.2%、51.5%、41.7%，运行时间与ORB+GMS+RANSAC算法相差很小，实时性较高。

图2 不同算法在Oxford图集上的CMR实验

表1 Bark图集各算法结果对比

图3 Bark数据集原图及各算法配准效果图

图2 中是根据选取特征点数量变化所得的CMR数据，可以从一定角度说明本文算法在该方面比其他三种算法更为出色。为了更严谨的体现本文算法的优势，对Oxford图集的单个子图集的所有图像进行实验分析，以模糊度对比方面为例，表2展示了选取同样数量的特征点，本文算法和ORB+GMS+RANSAC算法在CMR方面的差距，平均下来本文算法的CMR比ORB+GMS+RANSAC算法要高3.58%。

表2 Leuven图集测试结果对比

综上所述，本文算法在准确匹配率方面优于其他三种算法，且具有较高的实时性。

5 结语

本文针对GMS存在误匹配的问题，提出了基于GMS+GS_LMEDS的二次精匹配算法。该法利用高斯滤波预处理图像，再利用ORB特征提取，然后根据汉明距离进行粗匹配，最后使用GMS和LMEDS算法分别进行第一次和第二次精匹配。实验结果表明：相对于其他二次精匹配的算法，本文算法具有更高的准确匹配率，同时也具有较高的实时性。但本文算法在视角转变和尺寸变换这两方面的准确匹配率不高，如何使得在这些环境下获得更高匹配率是下一步要研究的方向。