基于运动学建模的自动瞄准系统

宋珣，马智博

（西安交通大学自动化系，西安710049）

RoboMaster全国机器人大赛是机器人竞技类比赛，在比赛中双方机器人需要用弹丸精准打击对方机器人的特定部位。近年来诸多参赛队伍意识到给机器人装配自动瞄准系统的重要性，同时每个队伍也都做了一定的反自动瞄准措施。多数队伍采用的传统自瞄系统在面对反自瞄措施时都会失灵，因此针对反自瞄措施的技术原理，提出基于运动学建模的自动瞄准系统，能够有效地弥补传统自瞄系统的缺陷。

自动瞄准；反自瞄；运动学

0 引言

在RoboMaster机器人比赛中，机器人的前后左右方向各有一块装甲板。机器人需要用弹丸精准打击敌方机器人的装甲板。打击的精确度是决定比赛的胜负走向的关键因素，所以近年来几乎所有队伍都开始给机器人配备自动瞄准系统，用以提升命中率。

大多数队伍的自动瞄准系统其原理和流程是相似的，大体都可以分为目标检测和运动预测两步。反自瞄系统基本是针对后者研制的，即利用自瞄系统中运动预测功能的缺陷，使得敌方机器人的自瞄系统在特定情况下失灵。本文将介绍一种在传统运动预测功能上有较大改进的自动瞄准系统，其综合效果良好，我们的参赛队伍在2019年RoboMaster全国机器人竞赛中获得一等奖。

1 基础模型

1.1 目标检测

目标检测是通过对摄像头捕获的图像进行处理，从而得到视野中敌方机器人暴露出的装甲板的空间位置。这是自动瞄准的首要步骤。比赛中的步兵机器人和其装甲板如图1所示。可以看到装甲板有一些明显的视觉特征，于是先通过颜色和亮度筛序出光条（图中数字5两侧的亮蓝色部分即为光条），再通过他们之间的几何关系匹配出可能是装甲板的组合，最后将可能的组合通过神经网络对其中间部分的区域进行判断，判断其是装甲板还是干扰组合，如果是装甲板则给出其数字，如图1中，装甲板数字为5。

图1 步兵机器人

判断出灯条组合确实为装甲板后，因为装甲板的真实尺寸是已知的，摄像头的内参矩阵也是已知的，所以能够结合装甲板在图像中的位置计算出其相对于相机的空间坐标。

1.2 坐标系建立

通过目标检测，得到了视野中的装甲板在相机坐标系中的位置，然而机器人的相机是跟随云台一起转动的，所以相机坐标系本身的方向是不断变化的。我们希望能够在一个方向不变的坐标系中研究目标的运动，所以就利用陀螺仪计算出一个方向不变的“绝对”坐标系，该坐标系的原点在己方机器人中心，方向始终固定在陀螺仪上电时云台的方向。

图2 坐标系转换关系

综上所述，在自动瞄准系统中，一共维护三个坐标系：目标机器人坐标系{XR,YR,ZR}，中心固连于己方机器人中心而方向不变的绝对坐标系{XI,YI,ZI}和相机坐标系{XC,YC,ZC}。其中{ }XI,YI,ZI和{XC,YC,ZC}的Z轴是同轴的，它们之间的关系如图2所示。因此，它们之间可以通过旋转一个角度θ来转换，θ可由陀螺仪测得的角速度做积分直接得到。设目标装甲板在相机坐标系中的位置为PC=(xC,yC,zC)，则它在绝对坐标系中的位置PI=(xI,yI,zI)可以由式（1）得到：

其中：

运动预测需要的是装甲板的绝对坐标PI，所以通过1式进行转换是目标检测的最后一步。需要的注意的是，这里的“绝对”不等同于真正意义上的惯性系。“绝对”只是代表其XI轴和YI轴的指向是不变的，但其坐标轴原点却是随己方机器人中心一起运动的。

1.3 运动预测

当得到了目标在绝对坐标系的位置后，最符合直觉的做法是：将云台转动至目标方向，然后射击弹丸。但摄像头的读图延迟tr、工控机的图像处理延迟tp和上位机到下位机的信息传输延迟tt会导致我们得到的目标位置总是滞后于目标每个时刻的真实位置。再加上子弹的飞行延迟tf，其结果是：当目标在运动时，子弹总会落在目标在前几个时刻的位置，命中率非常低。所以我们最好能够得到目标的运动规律，将各种延迟考虑之后计算出在保持原有运动规律的情况下几个时刻之后目标所处的位置，然后以该位置作为击打对象。

要得到目标的运动规律，就要用多个时刻的目标位置Pi(i=1,2…n)进行计算。例如，对于同一块装甲板，我们得到它在k个连续时刻的绝对位置P1,P2…Pk。假设目标进行的是匀速直线运动且k取8，则可以利用式3计算出目标速度，其中tmn代表m时刻到n时刻经历的时间之和。

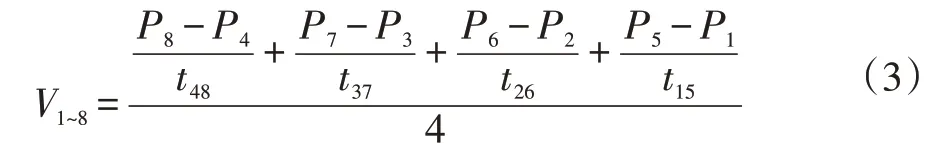
以上几种延迟之和∆t可由式4得到：则预测出的实际应该击打的位置Ppre是：

这种传统的运动预测方式的核心是假设目标做匀速直线运动，由于工控机有着较高的图像处理速度，处理效率可达70-80Hz，所以在几个时刻的时间段内实际只经过了不到100毫秒，在如此短的时间内假设目标做匀速直线运动确实是可行的，但面对后面提到的反自瞄措施时，此种建模方式会呈现出很大的弊端。

2 模型改进

2.1 反自瞄措施

大多数队伍采用的自动瞄准方式都如同上一章所述，且其中有相当部分的队伍连基础的运动预测都没有做。所以针对自动瞄准系统的固有弊端，即不可消除的延迟，几乎所有战队都给机器人设置了自旋模式，这就是反自瞄措施。

在开启自旋模式之后，机器人以每秒2到4圈的速度自转，且由于采用了麦克纳姆轮，在自旋的同时还可以进行水平移动。这样做可以使得机器人四周的四块装甲板轮流出现在敌人的视野中，且每块装甲板出现的时间很短，通常只有不到150毫秒。在自旋时装甲板的水平坐标XI实际上是一个正弦函数，在这种情况下，如果使用上一章的运动预测模型，则预测的打击位置大概率会落在敌方机器人外部，预测位置与真实位置的误差关系如图3所示。

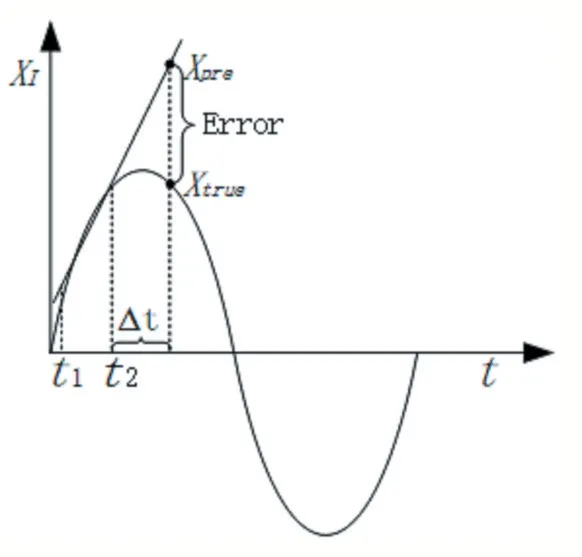
图3 预测位置误差

在图3中，我们选取t1作为计算目标速度的起始时刻，t2作为终止时刻，它们分别对应上一章的t1和tk，以此结合式（3）计算出目标的运动速度，如图中的直线所示，直线斜率即为在XI轴方向的运动速度。在t2位置的基础上，用预测的速度延后一个时间∆t，得到预测位置Xpre，然而实际的位置是Xtrue。它们之间的误差为Error=Xpre-Xtrue。在如此大的误差下基本是不可能打中的。

通过机器人的简化自旋示意图可以直观理解打不中的原因。如图4所示，图中ω代表旋转角速度，由中心处引出的两个箭头分别代表机器人在t1和t2两个时刻的正前方，本例中我们跟踪的是机器人右侧的装甲板。选取好t1和t2之后可以利用（3）式计算出装甲板速度Vpre。

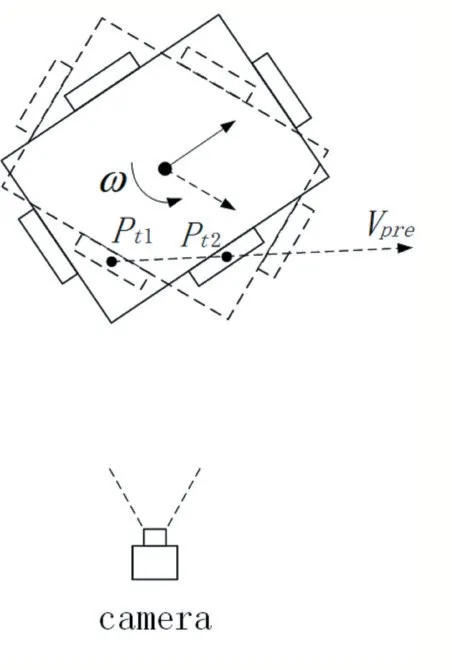
图4 简化自旋示意图

在t2位置基础上，以速度Vpre延迟∆t的时间得到预测位置Ppre，然而经过时间∆t之后跟踪的装甲板已经转到了我们看不到的侧面，所以这时已经不可能打中了，如图5所示。

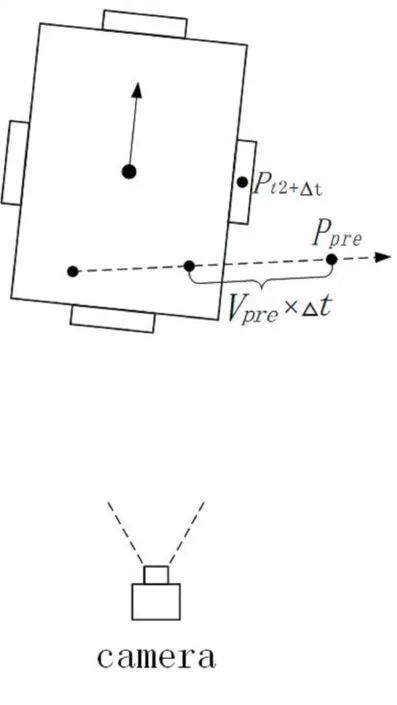
图5 预测位置示意图

2.2 运动学建模

由上一节分析可知，在敌方机器人开启自旋之后，如果我们想打中正在观察的装甲板，是很难的。这主要是由于当我们做出预测反应之后，被观察的装甲板已经消失在视野中了，所以这时无论用何种方式优化单一装甲板运动规律的求解方式都是徒劳的。

所以我们应当将注意力放在其他的装甲板上面，也就是说，虽然前几个时刻被观察的装甲板已经转到了我们无法射击到的视野盲区，但机器人的四周都有装甲板，所以会有下一块装甲板出现在视野中。如果我们知道了敌方机器人的几何参数和整体运动规律，则可以通过当前正在观察的装甲板来预测下一块装甲板的运动规律，转而将攻击对象变为下一块装甲板，这样就有充足的时间准备射击。从而可以有效提升命中率。

在确定模型参数之前，为便于分析，需要先确定一些假设条件。首先是假设目标机器人在自旋时会进行水平移动，且它相对于己方机器人的移动是匀速直线运动。其次假设目标机器人的自转速度是恒定的。最后假设目标机器人的4块装甲板的中心经过机器人的两条对称轴。通过我们进行的实验和对大多数队伍机器人的观察可以得出，这3条假设是合理的。

对于目标机器人，几乎所有参数都是未知的，所以需要列出所有我们感兴趣的参数，然后用观察到的信息进行建模和求解。需要的参数如表1所示。

表1 符号含义

运动学建模后机器人的表示如图6所示。

图6 运动学建模

若在某一起始时刻t1观察到目标装甲板位置为(XO1,YO1)，则可以写出式（6）的一组约束条件。

从起始时刻经过一个时间∆t之后，到达时刻i。则会得到式（7）的一组约束条件。

当然，式（6）可以看成式（7）的特殊情况，即∆t=0的情况。可以看到方程组的未知参数有：XC,YC,L1,θR,θV,V,ω。每一次观察会产生一组（2个）方程，其中XOi,YOi,∆t是已知的。所以理论上可以通过至少3次观察得到的6个方程解出6个未知参数。

不过在（7）式中，有非线性部分sin(θR+ω·∆t)和cos(θR+ω·∆t)，如果存在这样的非线性部分，会给求解带来很大麻烦。所以，使用一阶泰勒展开将其化为线性形式。一阶泰勒展开公式如式（8）所示。可以使用泰勒展开进行化简是因为我们是在一个很小的时间间隔内求解运动学参数，所以∆t也是较小的值。

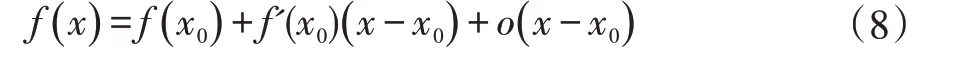
忽 略 无 穷 小 项o( x-x0)，得sin( θR+ω·∆t)和cos( θR+ω·∆t)在θR处的一阶泰勒展开为式（9）。

所以式（7）被线性化后的表示如式（10）所示。

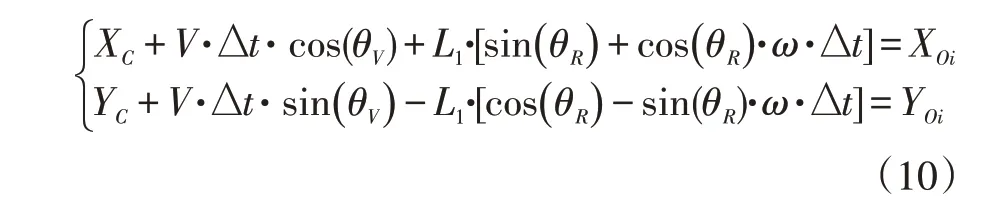
将式（10）写成矩阵形式是：

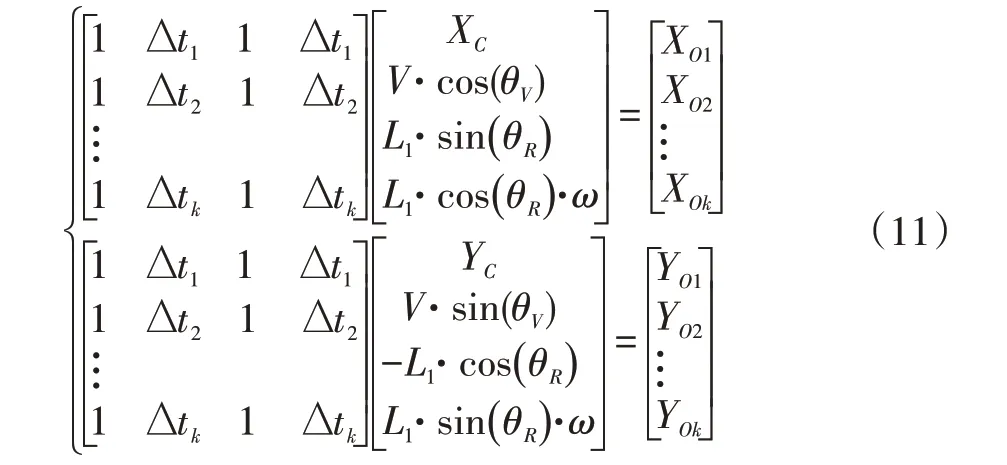
若k=4，则可以直接通过T1=K-1U1和T2=K-1U2求解。

若k≥4，则式（12）是一个超定方程。可以用伪逆求解。即：

当解出T1和T2之后，就可以很容易的解出XC,YC,L1,θR,θV,V,ω这6个未知数。同样，当下一块装甲板出现在视野中后，就可以计算出L2的值。如此，我们得到了目标机器人必要的几何参数和它的运动学参数。这样，通过当前正在观察的装甲板的位置，可以推知该机器人剩余三块装甲板的位置和它们在将来一小段时间内的运动轨迹。于是，可以预测还未出现在视野中的装甲板在将来几个时刻的位置并对其进行击打。而不是像上一章的运动预测系统——预测和射击仅局限于被观察的一块装甲板。在目标机器人自旋时，一块装甲板被观察并计算出运动规律之后，很快就会消失在视野中，所以传统运动预测系统面对自旋时效果极差。而引入运动学建模的运动预测系统将装甲板的观测与射击分离，就较好地解决了该问题。

2.3 卡尔曼滤波

上述运动预测过程是在下位机完成的，下位机使用k组观测进行计算就需要从上位机接收k次数据。受摄像头帧率的限制，上位机产生两组有效数据的时间间隔大约是14毫秒，如果中间目标检测环节受到干扰，数据间断的时间还会更久，即数据更新频率在70Hz以下。然而如果下位机对云台的控制频率也保持在70Hz上下，会产生较大的延迟和抖动。所以下位机需要在两组有效数据的时间间隔内通过已有数据自行生成控制指令，这就需要通过目标机器人几何参数和运动规律生成状态转移方程，假设通过最后一次有效数据计算出的参数为XC,YC,L1,θR,θV,V,ω，则在基础上经过∆t的时间，目标右装甲板位置(Xrnew,Yrnew)的计算如式（14）所示。目标后装甲板位置(Xbnew,Ybnew)的计算如式（15）所示。

当下一帧有效数据到来时，会产生一个观测。如果是右侧装甲板的位置观测(XrO,YrO)，则通过卡尔曼滤波将观测状态PrO=(XrO,YrO)与预测状态Prnew=(Xrnew,Yrnew)进行融合，如式（16）所示。

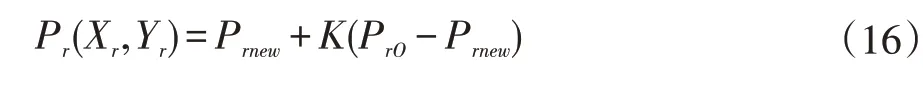
其中K=F(F+R)-1，为卡尔曼增益。F为状态Prnew的协方差矩阵，R为观测噪声的协方差矩阵，在实践中可以通过距离调整R的值，因为一般来说距离越远其观测误差越大。使用卡尔曼滤波进行状态更新可以使得控制信号更加连贯，也使得位置数据更新更加平滑。

3 结语

本文给出了基于运动学建模的自动瞄准系统。相较于传统自瞄算法，该算法对观测数据做到了更好的利用。通过对目标车进行运动学建模，预测和射击不用局限于同一块装甲板，从而大幅提升了实际效果。最后通过卡尔曼滤波使得控制更加平滑。该自瞄系统在比赛中表现良好，具有一定的实际意义。