一个费马数分解算法的剖析与优化

王珏

（广东移远通讯技术有限公司，佛山528042）

分析一个费马数分解算法中的冗余步骤，给出相应的优化结果。针对相关文献述及大费马数表示困难的问题，给出利用GMP大数运算库表示大费马数的一种方法。基于数学软件Maple，进行解析费马数小因数的试验。试验表明，优化后的算法可提高计算效率。

整数分解；费马数；算法；密码学

0 引言

算法，始终是程序设计人员关注的话题。作为一个程序员，工作之余了解一下国内外与算法相关新闻、报道和事件，不失为另一类娱乐。最近看到Journal of Software（JSW）期刊上新出的一篇有关分解费马数的论文[1]，觉得很有意思，便仔细研读了一下。该文介绍的是一个分解费马数的新方法，在理论上分解任何Fn（n>100001）的任何费马数。众所周知，费马数是数论里面一类受人关注的数，国内学术期刊也多有研究报道。例如，文献[2-3]较为通俗地介绍了费马数的历史与发展，文献[4]较为系统地研究了费马数。也有学者对费马数的性质进行挖掘分析，如文献[5-12]分别就费马数的因数性质进行了探讨。在分解计算方面，文献[13]介绍了利用椭圆曲线分解F7和F8的过程，文献[14]则介绍了国外分解计算的情况。国外有专门的网站介绍分解费马数的进展，如文献[15]。从笔者不是十分专业的角度来看，除了目前看到的文献[1]，国内学者对于研究费马数分解算法的不多。

鉴于此，笔者对文献[1]给出的算法进行了认真分析，发现这个算法虽然很巧妙，却也存在可以改进的地方。本文介绍笔者的分析和改进结果。

1 问题的提出及解决方案

1.1 问题的提出

仔细研读并按照文献[1]给出的算法在Maple软件编程时，会发现该文存在几处可以优化的地方。首先是该文在结论和展望部分提出的二个有待进一步解决的问题：一是大数运算工具的问题，二是确定算法中的参数c实现加速计算的问题。该文还列举了m>23时，GMP大数库和Maple都出现溢出的情况，可以推断该文应该是在利用目前常用的GMP大数运算库进行了C/C++编程测试和利用Maple数学软件测试时遇到了计算溢出。该文同时也指出NTL大数运算库和MIRACL大数运算库都不能完成运算。于是该文作者显得无可奈何地说，这些工具的开发已经超出了他的能力范围。诚然，开发大数运算的工具，的确超越数学家们的工作范围。

一个值得注意的事情是，文献[1]在JSW上正式发表以前有个Preprint版本，公开在文献[16]。在这个Preprint版本中，作者哀叹说所遇到的困难是，在m>2w-1时无法用GMP大数库来表达Fn导致不能计算大费马数的分解，这里w是计算机的字长。而在JSW正式发表的版本里，作者已经没有这个哀叹了。说明该作者已经利用GMP大数库解决了大费马数的表示问题了，反而是在mpz_gcd这个库函数上遇到了新的问题。笔者经过分析，也找到了一个表示费马数的方法。鉴于文献[1]没有列出它采用的方法，本文在后面小节给出笔者的方法。

对于第二个问题，即确定算法中的参数c实现加速计算的问题，该文作者没有进行多的说明，仅仅呼吁更多年轻人来参与解决所述问题。分析文[1]对c的几处说明，发现这是一个减少搜索次数的参数，这是因为它满足b=■ ■log2N-χ，且在几个搜索过程中都出现了for ifromb downto3 do的语句。

鉴于文献[1]没有详细介绍这个参数的选择而是把它当成一个问题提出，笔者通过研究并经Maple编程测试，发现了一些规律，后文将给予介绍。

除了前述两个问题之外，文献[1]还存在可以挖掘的地方，那就是具体分解费马数的Procedure 4。笔者经研究发现，这个过程存在两个可以优化的地方。一个是该过程中的参数a的上限，二是该过程中的基本计算。详见后文介绍。

1.2 解决方案

本小节给出大费马数的表示方案、文献[1]中Procedure4的优化方法以及参数c的选择方案。

（1）大费马数的表示

针对前小节的第一个问题，笔者经仔细分析NTL大数运算库和MIRACL大数运算库的文档发现，这两个库的确无法表示大费马数。经分析GMP大数库的文档发现，利用mpz_ui_pow_ui和mpz_pow_ui两个库函数，可以解决大费马数的表示问题。mpz_ui_pow_ui和mpz_pow_ui两个库函数的原型与功能分别如表1所示。

表1函数原型与功能

利用这两个函数，可以实现大费马数的表示。具体思路如下：

对于任意无符号长整型的数m，利用Euclid除法将m按照计算机的字长w表示成

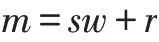
式中s≥0，0≤r＜w均为整数。

令P=2r，则P是可以表示的。再利用mpz_ui_pow_ui（M，2，P）计算一个大整数M=2P。

显然，若s=0则m=r且M=2P=22r即为所计算的费马数。

若s>0，采用先记录M=22r，比如记录到T，即T=22r。下面置P=2w，则P也是可以表示的。此时可以 利用mpz_pow_ui（U，T，P）计算出 一 个U=TP=(22r)2w=22r+w。可见，在每次将U置于T循环s次就能得到U=22r+sw=22m。

到此为止，利用GMP大数库在理论上（GMP库的有效范围内）可以表示任意费马数了。

（2）长字长系统方案

文献[1]表明它的试验在Windows XP平台用Maple和C/C++测试止于F23。根据前小节的推算，这是极有可能的。因为Windows XP是32位操作系统。笔者在64位Win7系统用Maple软件测试发现，计算F29时是可行的，但是F30就出现溢出。由此可以推断，利用长字长OS系统可以计算更多的费马数。当然这种方法只能取决于计算机系统的发展，与目前分解费马数采用的网格计算[17]是不可比的。

（3）分解算法的优化方案

文献[1]给出的分解费马数过程Procedure4是建立在该文求对一般形如2au+1因数的算法上的。分析Procedure 4，可以发现有些冗余。其实对费马数而言，输入参数就是n和c，根本不用计算n=■l og2log2(N-1)■和b=■l og2(N-1)■-χ。这样一来c就是一个关键。这也是文献[1]所指出的问题之一。另外，文献[1]发现了局部变量a是有界，因此它给出a=m+20的估算。笔者认为该作者没有注意到文献[15]里面列出的表2。

表2 参数a取值与频率

可见，文献[1]建议a=m+20可以改为a=m+13。（4）c的选择方案

根据文献[1]的陈述，c是算法里面的一个输入参数。前面小节已经述及，这是减少搜索次数的参数。文献[1]有几个地方介绍了这个参数的来由：

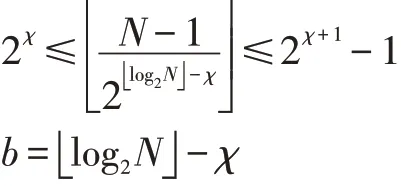
并且指出，若事先能估值u的范围，那么c原则上应满足u>2χ。

根据这个原则，结合文献[15]所列举的各费马数数的u值，笔者建议对于小费马数，c的上限取值如表3所示（表中除去了F14、F20、F24三个小于F29缺失u之范围的数）。

限于篇幅这里不一一列举其他。按照这个规律以及文献[15]所介绍u针对m的分布范围，选择合适的c是不成问题的。笔者在Maple里面的实验结果也证实了这个方案的有效性，详见后文。

表3 各费马数c的上限建议值

2 算法与实现

本小节根据前述优化方案，给出分解费马数的优化算法，并给出在64位Maple下的实验结果。

2.1 算法

在文献[1]给出的Procedure 4过程中，输入的参数是N=22n+1与c，然后通过公式n=l og2log2(N-1)、b=l og2(N-1)-χ和a=n+20来计算出n及至b和a。事实上，对于费马数而言，这些计算显得冗余。另外，原过程中的计算也可以直接优化为l=22n-i-1,r=22n-i+1+1。如此优化，还避免了浮点计算。这里给出优化后的算法如下。

算法：解析费马数小因数的算法

2.2 Maple实现的效果

基于前述改进的算法，在一台配置Intel E5645@2.4GHz CPU、8G内存、Win7 64位台式机上进行实验，选择Maple-64位软件编程，参照文献[15]的结果，一些费马数寻找其小因数得到表4的运行结果。

表4 若干费马数及其分解情况

3 结语

对比文献[1]的表1、文献[15]的清单以及本文的表4可得到以下结论：

（1）文献[1]的算法的确能够找到费马数的小因子，对于较小的u也是非常快的算法，但是也存在优化的空间。本文进行的优化也证明了这一点。例如，文献[1]花了50496步搜索找到了F6的因子274177而经本文优化后仅化了28步，文献[1]花了4034686步搜索找到了F10的因子45592577而经本文优化后仅化了1474步，文献[1]花了1606849步搜索找到了F19的因子70525124609而经本文优化后仅化了435步。

（2）大数表示和计算的工具实为非常紧迫的需要。文献[1]表示利用GMP大数库运算在32位系统只能计算到F22。笔者在64位系统利用Maple也只能计算到F29。须知，Maple也是采用GMP大数库作为其内核运算工具的。因此，完善大数表示和计算的工具实为非常紧迫的需要。

（3）更多更高效的算法仍需开发。文献[1]的算法和本文优化的算法，总体上还是适合较小的u。当u较大时，如F7的u为116503103764643，所需O(0.25×116503103764643×214)=O(238598356509988864)的计算量。采用2.4GHz主频的计算机需要运行约99415982秒（27615小时»3年）才能算出结果。其次，文献[1]及本文算法的时间复杂度为O(0.125u(log2N)2)。注意到对于费马数Fm而言，其计算量为O(22m-3u)因为log2Fm=2m，依然是巨大的计算量。笔者没有研究国际上目前采用的网格计算方法，但是从其几个月甚至1年多才产生一个新结果的进度来看，优秀算法依然可期。

综上所述，尽管从理论上，文献[1]和本文算法可以有效析出费马数的小因数，更快的算法还是值得研究的。笔者考虑是否在并行和超级计算方面能否开发出合适的算法。限于知识的制约，希望未来能看到相应的成果。