基于矩阵分解的记忆网络模型

朱馨培

（哈尔滨陆军预备役炮兵旅，哈尔滨150000）

现有的两类推荐模型（基于循环神经网络的推荐模型和基于协同过滤的推荐模型）将用户编码在一个低维想两种，限制了用户偏好的记忆能力。为增大模型记忆空间，匹配用户需求，提出基于混合矩阵分解的记忆网络模型，在基于矩阵分解的框架下混合使用深度神经网络和记忆网络，得到两个层级的用户表示。

矩阵分解；神经网络；记忆网络；推荐模型

0 引言

矩阵分解技术广泛应用于协同过滤推荐模型中，该算法使用低维空间的向量编码用户和物品，并将向量的点积结果作为用户对物品的喜好程度。对于用户来说，他的喜好往往是复杂多变的，将用户兴趣压缩到一个向量中既存在信息丢失的问题，又不能够表示出用户喜好的动态性和复杂性。另外，现有研究表明，用物品向量和用户向量之间的点积来表示结果的方式没有考虑到用户和物品之间的交互关系。所以，需要对用户和物品之间的交互进行建模，得到用户的物品级别的表不。本文首先介绍了传统的矩阵分解模型，然后介绍如何改进矩阵分解的两个缺陷，并在此基础上提出混合矩阵分解和记忆网络模型（下文简称记忆网络模型）。

1 算法实现

矩阵分解是基于隐因子模型的一种协同过滤算法。隐因子可以理解为用户对物品喜好的潜在原因或者物品的潜在特征。该潜在特征可以通过学习物品-物品、用户-用户或用户-物品的交互关系而得到。把每一个潜在特征作为用户或物品编码的一个维度，则用户或物品就可以表示为一个大小为潜特征因子的向量。如果把隐因子数量设置为3，矩阵分解可以表示为：将已有的用户-物品交互矩阵R分解为两个低维的用户隐矩阵P和物品隐矩阵Q，原矩阵中每一个单元格的数值由对应行列的隐因子向量的点积所得。

上文中所述的用户-物品交互矩阵是用户的评分矩阵，它表示的就是在该系统中的用户对于购买过的物品的总体评分。评分在推荐系统中属于显示反馈，显示反馈的信息往往会比较稀疏，所以只基于显示评分的矩阵分解往往也不会有太好的效果。为了改进这一点，许多模型把矩阵中的显示反馈信息改为隐式反馈，即把用户的购买、评分、浏览等不同的行为统一成一个反馈信号-用户与该物品交互过。如果用户和物品交互过，则对应的单元格的值设置为1，否则设置为0。

对用户和物品实体，使用大小为D维的向量来表示。对应的M个用户和N个物品分別可以表示为P∈ℝM*D和Q∈ℝN*D的矩阵，矩阵中的每一行表示一个用户或物品，矩阵分解的表示方法为：

Rˆui的内容可以表示为PuQTi使用预测的矩阵中的值拟合原有矩阵中的已有数据，并且基于平方损失函数等目标函数对用户和物品矩阵进行优化，加入L2正则项的目标函数如下：

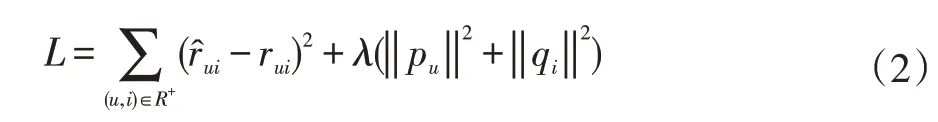
在目标函数的基础上，通过随机梯度下降等优化方法优化P、Q矩阵。最后，使用相应用户向量和物品向量的点积作为该用户对该物品的评分预测，并根据评分的高低在未消费物品中选择最高的几项推荐给用户。

2 记忆网络模型框架

为了解决引言中提出的原始矩阵分解算法的两个缺点，本文混合使用特征记忆网络和多层全连接网络，得到记忆网络模型。

模型结构如图1所示，模型的核心是得到用户的物品级和特征级的向量表示，并将这两者综合起来求解用户对物品的喜好。下面分別介绍求解这两个向量表示对应的模块。

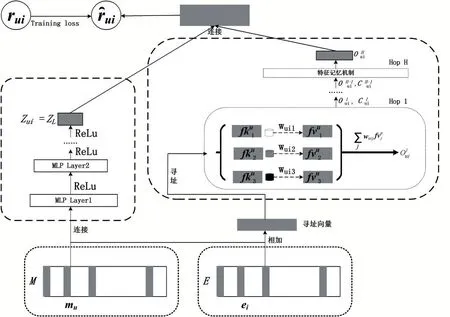
图1 记忆网络模型整体框架

2.1 MLP模块

在上节介绍中，传统矩阵分解将用户和物品映射到同一个向量空间，再采用向量内积的方式求用户和物品的相似度。向量内积可以看作是未归一化的夹角余弦距离，即以向量之间夹角衡量向量的距离。该方式一方面不能够表达用户物品之间的交互关系，另一方面也会带来距离求解上比较大的损失。表1是假设的用户之间的相似度，可以知道s23(0.66)＞s12(0.5)＞s13(0.4)。根据该关系大小，可以将三个向量的位置关系表示在空间中如图2所示。此时考虑新用户u4，可以知道相似度排名是s41>s43>s42。在u4与u1最相近，需要放在离p1最近的前提下，无论怎么放p4，都会使得p4与p2的距离比与p3的距离近，这会导致巨大的排序损失。综上，为了解决矩阵分解存在的这个问题，本文使用DNN来学习用户物品之间的交互特征。由于该网络学习的是用户和物品的交互关系，所以将网络最后一层的输出作为用户的物品级表示。

表1 用户相似度

图2 用户向量分布形式

如图1左半部分所示，该模块的输入是[mu;ei]，“；”表示两个向量首尾相连，将其输入到多层全连接网络之后，通过神经网络学习到用户和物品的高阶交互特征。最后将神经网络的最后一层输出zL作为用户的物品层的表示zui该神经网络的具体定义如下：

其中，Φ表示非线性激活函数，在FMN中使用ReLU作为模型的激活函数。神经网络的激活函数包括sigmoid、tanh、ReLU等，其中sigmoid函数将每个神经元的值x通过公式映射到0到1之间。一方面这种方式将值映射在一个小的数字区间会限制神经元的表达能力，另一方面从该激活函数的函数图像可以看出：在x的值非常大或非常小时，该激活函数的梯度接近于0，此时神经元停止学习。tanh激活函数是sigmmd激活函数的改进版本。神经元的输出在-1和1之间，但是由于tanh（x/2）=2σ（x）-1它也只能在一定程度上缓解sigmoid饱和的问题，而不能消除。ReLU在负数区取0，正数区直接输出原值，这种计算方式比前两者收敛更快，且不存在饱和的问题（正数区梯度始终不变）。综上，在隐藏层的激活函数选择上选择Re-LU效果会更好。Wx、bx是第x层隐藏层的权重和偏罝参数。本文使用最后一层的输出结果作为用户的表示，zui=zL,zui∈ℝd并使用和文献中一样的塔式结构。塔式结构是一种在最低隐藏层拥有最多神经元数量，剩余每一层在前一层基础上递减的网络结构。通过在高层使用数量更少的神经元的方式，可以学习到数据的高阶交互特征。除了输入层的向量大小为2d之外，隐藏层从低到高倍减神经元数目。

2.2 特征记忆网络模块

在文献[5]中，用户、物品的向量的每一维度表示该实体的一个特征，使用一个低维空间的向量表示其潜在特征因子。该方法的缺点是：一个向量不能充分编码所有用户信息。一种解决方案是增大向量维度，但是有可能会导致对训练数据过拟合从而使模型的泛化能力降低。受文献[2]启发，将每一个特征因子看作一个独立的向量，用户对物品的喜好表现的是用户对物品存在的某些特征的喜好。这样一来，通过预先定义好的总特征数量，每个物品的表示是由某几个特征组成，而用户的喜好表示则是对不同特征的喜好程度的累加。为了更好的存储用户对特征的喜好，该模块使用记忆矩阵存储用户对特征的偏好，其整体结构如图2右半部分所示。

从整体上看，网络中包含四个记忆矩阵：每个用户的特征寻址矩阵、特征记忆矩阵、物品的表示矩阵和用户的表示矩阵。具体地，用户u的记忆矩阵为FKu∈ℝKxd、FVu∈ℝKxd和M∈ℝPxd，其中K是定义的总特征数，d是每个记忆片段的大小。在用户额外的记忆矩阵M∈ℝPxd中，P表示用户数量，每一行表示一个用户。物品的记忆矩阵为E∈ℝPxd，Q表示数据集的物品数量大小，矩阵E中每一行表示一个物品。

数据的输入形式为（用户,物品）二元组，本文采用与文献[34]中相似的方法得到用户在该物品下对特征的喜好。对每一个输入数据对（u,i）来说，物品i带来的用户u对每个特征的偏好表示为puij，它的计算方式

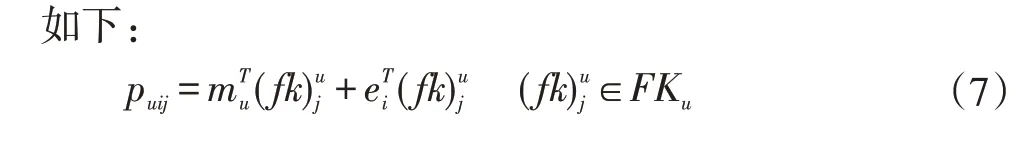
公式的第一项表示目标用户u对第j个特征的偏好。第二项表示物品i造成的用户对该项特征的喜好程度的置信度的偏移。因此，整个寻址方式表明用户u在物品i的影响下，对特征j的喜好程度。用户对每个特征都有不同的偏好程度，在用特征记忆向量表示用户时，不能赋予每个特征相同的权重。模型中的注意力机制可以学习到一个动态权重值，将注意力集中在特征集合的部分子集当中，从而以加权和的形式表示用户。

该公式生成了用户在特征上的归一化权重分布。注意力机制的引入，使得用户在自己喜好的特征上获得更高的分值，在无关的特征上投入更少的关注。接着模型再使用该权重得分乘以存储的特征记忆单元得到用户的特征级表示：

其中，(fv)uj寻址矩阵中对应的特征记忆单元。这种外存机制允许模型在存储用户对特征的长期喜好的同时，还能根据存储的内容和当前物品的信息动态更新记忆。从另一个角度来讲，模型首先通过制定的寻址方案，从寻址矩阵FKu中学习用户对每个特征的偏好权重，再对存储在特征记忆矩阵FV中的相关记忆进行加权求和。记忆网络动态选取相关的特征子集，并将加权和的结果作为用户的特征级表示向量。

在上面提到的工作中，用户的权重偏好是由简单的（用户,特征）向量点积加上（物品,特征）向量点积而得。考虑到该方式有可能不能一次性获取到所有相关信息，本文采取多层记忆网络的形式来获取与用户最相关的特征信息。将记忆网络拓展为多层结构，每一层的记忆更新中，借助前一层给予的信息重新搜索整个特征集合，更新记忆的权重值。这种结构一方面可以在较高层中修正在低层中由于对信息的错误理解而导致的错误结果，另一方面可以借助更多的先验知识，提取出之前未发现的关键信息，每一层得到特征权重的方式如下：

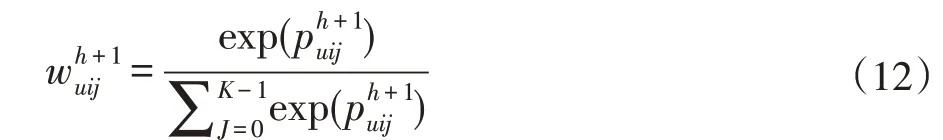
其中，Wh、Uh是参数方阵，将上一层的信息和当前层的输出映射到同样的向量空间，再通过非线性激活函数得到当前层的候选输出。然后将候选输出作为寻址的查询向量，将其与寻址向量做内积得未归一化的权重。记忆网络的第一层的寻址输入为

2.3 输出模块

前两个模块分別在物品级和特征级编码用户，最终的输出模块将两者综合起来得到用户对物品的喜好预测。所以，对于给定的用户u和物品i，物品的得分计算方式如下：

“;”表示向量连接，v∈ℝ2d是在训练过程中需要学习的参数。

最后，本文选择交叉熵损失函数作为模型的目标方程。最小化该目标方程，并且根据链式传导法则去优化模型中涉及到的各个参数，

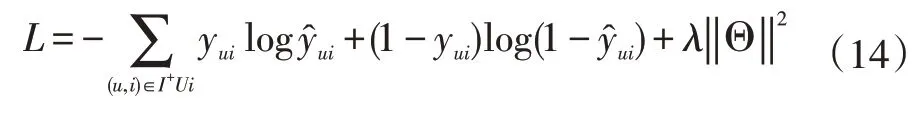
3 结语

本文从介绍传统的矩阵分解算法开始，详细介绍记忆网络模型每个模块的功能。综上所述，本文提出的记忆网络模型相比传统协同过滤等推荐算法有以下优势：

第一，用户的物品级表示模块可以通过MLP获取用户和物品之间的非线性交互关系，并且对相似用户之间的距离有一个更好的度量方法。

第二，用户的特征级表示由记忆网络中存储的特征进行加权和得到，这种表示方法集成了多个特征的信息，解决了矩阵分解模型中使用单一向量表示用户的问题。