基于数据融合的CNN方法用于人体活动识别

韩欣欣，叶 剑，周海英

(1.中北大学 大数据学院，山西 太原 030051；2.中国科学院计算技术研究所 泛在计算系统研究中心， 北京 100190；3.中国科学院计算技术研究所 移动计算与新型终端北京市重点实验室，北京 100190)

0 引 言

借助与人体活动信息有关的传感器、图片或视频来获得活动的相关特征，从而解决人体活动识别(human activity recognition，HAR)问题。近年来，传感器技术和处理传感器数据的技术均取得了显著的进步。在移动设备中嵌入小巧的、轻便的传感器也变得普及，较大推动了研究热点转向借助传感器数据解决HAR问题[1]。深度学习在图像识别和语音识别方面的出色表现，促进了深度学习在基于传感器的HAR的运用，且已有研究人员证明运用深度学习可以获得较好性能[2,3]。

三轴加速度计是基于传感器的HAR中较常使用的传感器[4]。已有研究者发现轴之间的相关性能够提高活动识别的准确率。例如，使用合成加速度来减少由于移动电话的不同放置位置引起的旋转干扰[5,6]。排列传感器数据以生成在一定程度上考虑了轴之间相关性的活动图，通过将传感器的时间序列信号转换为包含轴间相关性的活动图像，模型的识别准确率得到明显提高[6,7]。然而，以上方法的提出依赖于研究者自身的知识和经验，在一定程度上具有局限性。

本文的目的是减少存在的局限性同时更好地利用轴之间的相关性。因此基于数据融合的卷积神经网络(convolutional neural network，CNN)方法在本文中被提出。该方法运用单通道数据融合方法获得包含轴之间相关性的融合数据。然后将数据输入到CNN中进行特征的提取和活动的分类。本文方法能有效利用轴之间的相关性并提高模型的分类准确率。本文使用WISDM公开数据集对网络结构进行测试，实验结果表明，提出的方法在准确率方面优于CNN。

1 单通道数据融合方法

单通道数据融合方法如图1所示。若传感器的数据形如一张二维图片，即其仅有一个通道，则将其视为单通道格式。本文使用的传感器为三轴加速度计，将三轴加速度数据按行排列。图1中的输入层中的数据共有3行。本文提出的单通道数据融合方法是将按行排列的三轴数据利用 3×1 卷积进行融合，可看作是数据融合的操作。对三轴加速度数据进行数据融合操作，能够得到形为(1,200,1)的融合数据。可根据需要对三轴加速度数据重复进行数据融合操作以得到相应个数的融合数据。如果融合数据的数量是n，说明执行n次3×1卷积运算。

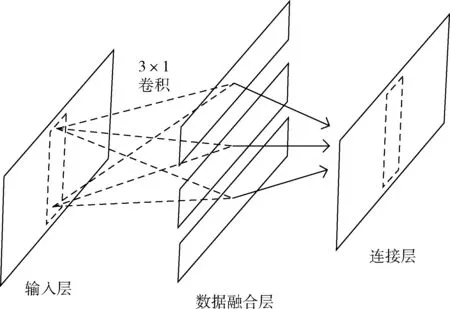
图1 单通道数据融合方法

2 基于数据融合的CNN方法的实现

2.1 基于数据融合的CNN方法

本文提出的基于数据融合的CNN方法的总体流程如图2 所示。首先通过单通道数据融合方法将加速度数据变为包含轴之间相关性的融合数据。然后通过CNN对融合数据进行特征的提取和活动的分类。

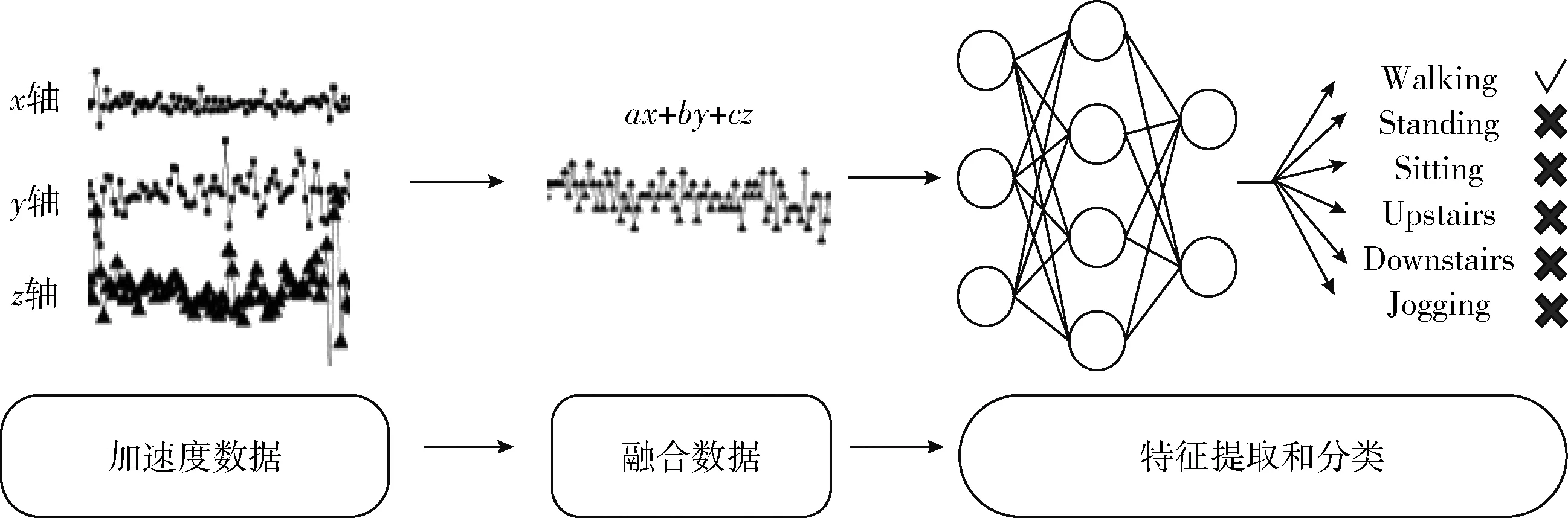
图2 基于数据融合的CNN方法的总体流程

CNN包括卷积层、池化层、全连接层和Softmax层。卷积层的个数、池化层的位置、全连接层的大小等会导致网络结构的不同，不同的网络结构可能会得出不一样的结果。CNN在人体活动识别领域得到了广泛运用。如文献[8]中作者提出了一个使用CNN实现的基于加速度计的人体活动识别方法，实验结果表明其准确率高于支持向量机和深度信念网络的准确率。

卷积层：卷积层的作用是提取特征。卷积层的特点有两点：局部连接和权重共享。卷积层中的神经元与上一层特征图中的局部区域相连接，卷积核和上一层中的局部区域执行点积运算产生的输出值是卷积层中的一个神经元。卷积的结果由等式(1)计算得到。对卷积的结果使用激活函数以向网络中引入非线性。

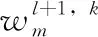
(1)

(2)

池化层：池化层结合了语义相似的特征，以在下一层中生成单个神经元[9]。平均池化选取输入数据的局部区域的平均值作为输出值传递到下一层。最大池化则是选取输入数据的局部区域的最大值作为输出值传递到下一层。

Softmax层：Softmax层的作用是将数据映射到 (0,1) 区间内以判断最终结果的类别。因此解决分类问题时，Softmax层通常放在卷积层、池化层、全连接层的后面，即模型的最后。Softmax层中的神经元个数与分类任务中类别的个数相同。Softmax函数如等式(3)所示

(3)

CNN-DF(基于数据融合的CNN方法)如图3所示。首先执行数据融合操作以获得包含轴之间相关性的融合数据。假设生成n个融合数据，每一个融合数据的大小均为(1,200,1)。对每一个融合数据分别进行卷积和池化操作以提取特征，其中卷积层的卷积核大小为1×7，卷积核的个数为50，池化层的步长为1。接下来的连接层将融合数据中提取到的特征逐行连接，生成的数据的通道数与池化层中数据的通道数一致。CNN中1维卷积核仅能考虑到数据的局部依赖性，2维卷积核与其相比还可以考虑到空间依赖性[10]。因此，对连接层的数据执行n×7的卷积操作和池化操作。池化层的输出数据经展平层将数据一维化后与Softmax层中的神经元连接，获得输出结果。

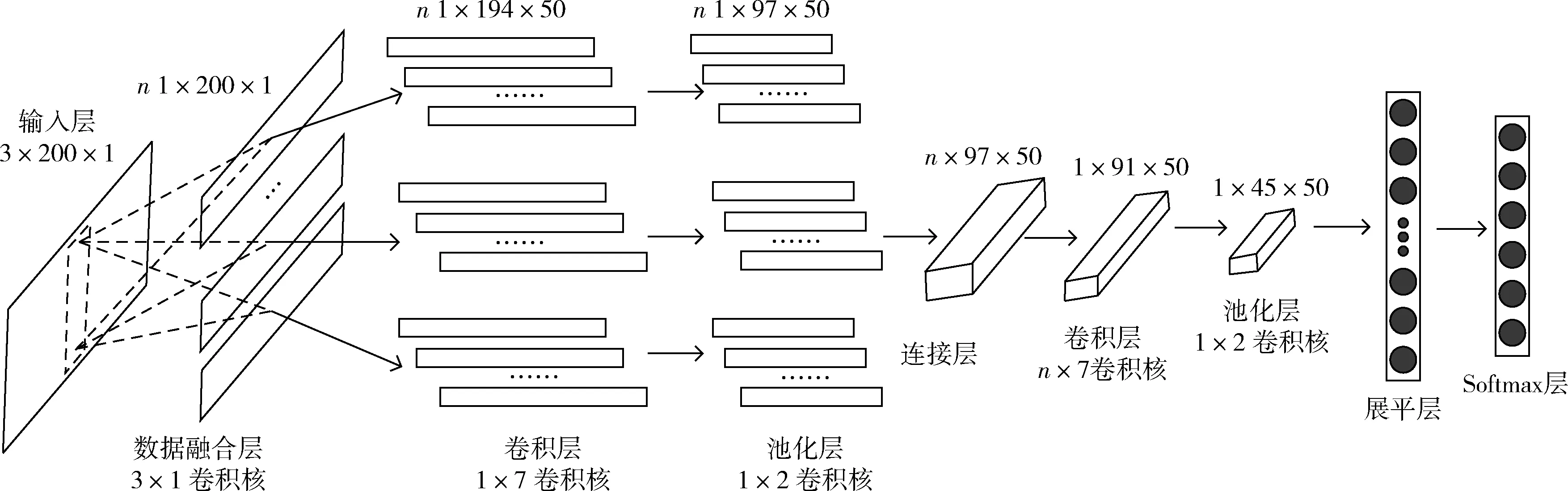
图3 基于数据融合的CNN方法

2.2 学习率控制方法

Learning Rate Schedule：在对分类准确率有一定影响的超参数中，学习率是最重要的超参数之一。若设定的学习率太大，那么损失曲线可能存在一定范围的波动甚至上升。若设定的学习率太小，可能导致所需的实验的迭代次数较多。本文使用根据迭代次数动态变化的学习率。先在训练伊始将学习率设定为相对较大值，使得模型的准确率能够在较短时间内收敛到理想状态。然而损失和准确率曲线可能会有一定的大幅波动。于是在训练的中间阶段将学习率减小，使得模型继续学习有用信息且曲线的波动幅度变小。在训练的后期阶段，学习率进一步减小，曲线的波动幅度继续变小。该方法能够加快模型的训练速度、降低过拟合程度和减少实验的迭代次数。

2.3 实现算法

算法1展示了实现本文提出的方法的伪代码。在本文中，形如(1,200,1)的融合数据个数和数据融合层中的 3×1 卷积核的个数相同。

算法1：基于数据融合的卷积神经网络方法

注释:

NC:融合数据的数量

输入:标签数据集 {(xi,yi,zi),ai}, 无标签数据集 {(xi,yi,zi)}

输出:无标签数据集的活动标签

重复

前向传播:

i←1

for每个标签数据 (x,y,z) do

whilei≤Ncdo

使用等式(1)对输入数据执行数据融合操作

使用等式(1)和式(2)对融合数据执行卷积操作

对卷积层的输出执行最大池化操作

i=i+1

end while

逐行连接池化层的输出数据

使用等式(1)和式(2)对连接层的数据执行卷积操作

对卷积层的输出执行最大池化操作

end for

使用等式(3)进行分类

反向传播:

使用随机梯度下降算法执行反向传播

直到权重收敛;

for每个无标签数据 (x,y,z) do

使用训练好的网络预测活动标签

end for

2.4 CNN-DF与CNN的比较

本节比较CNN-DF与CNN中第一个卷积层的输出值之间的差异。图4和图5分别展现了两种方法从输入层到卷积层的变化过程。在图4和图5中，输入层中的虚线框代表卷积核，卷积层中的虚线框表示卷积运算的输出值。为了简化等式，在本节中不考虑偏置项。

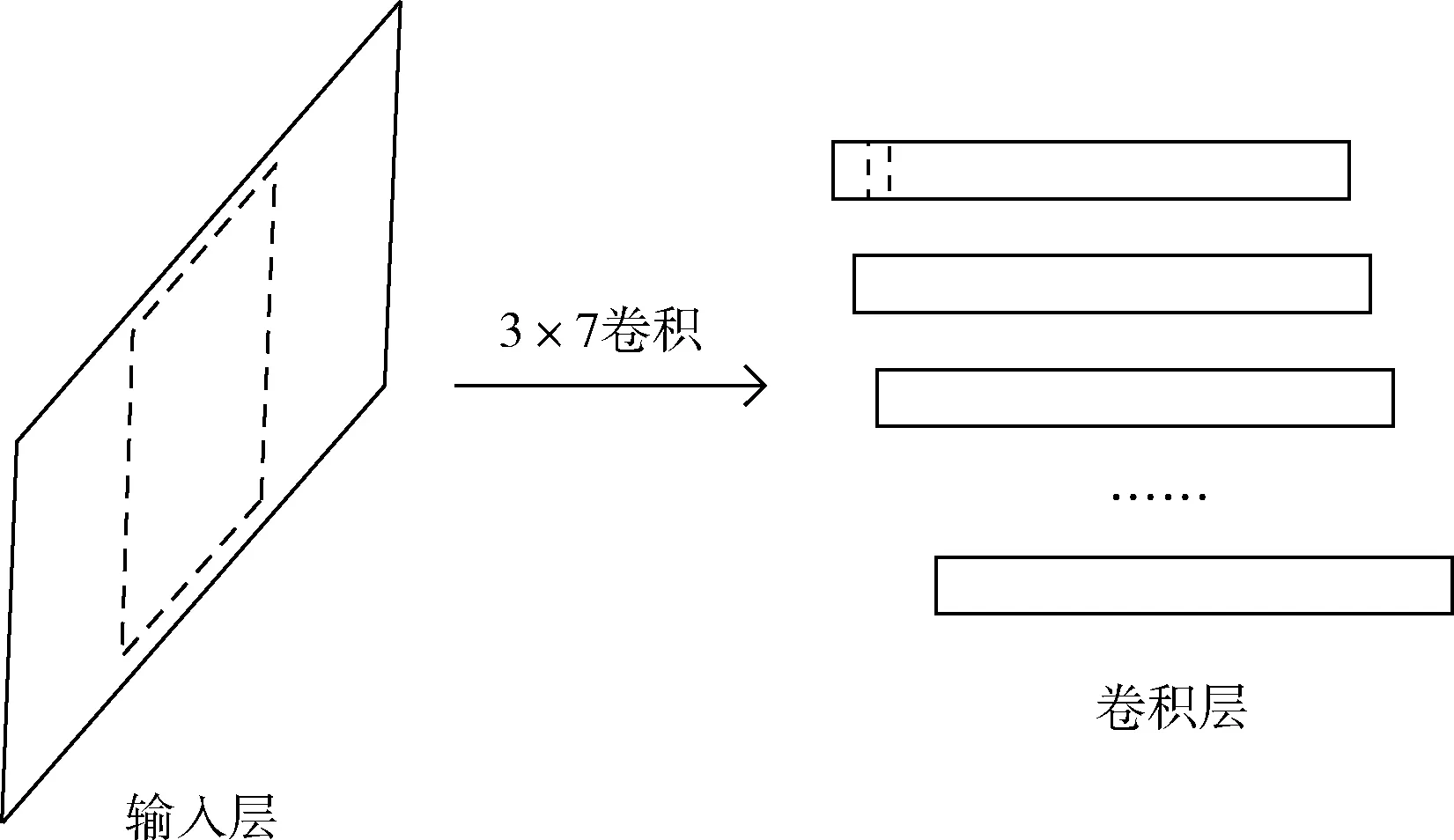
图4 CNN的输入层和卷积层

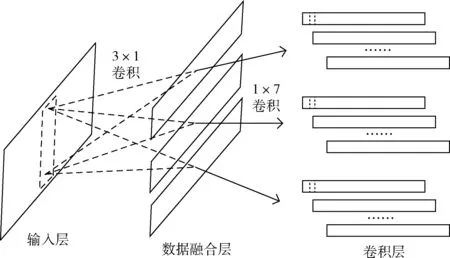
图5 CNN-DF的输入层，数据融合层，连接层和卷积层

对于图4，将 [[x1,x2,x3,x4,x5,x6,x7], [y1,y2,y3,y4,y5,y6,y7], [z1,z2,z3,z4,z5,z6,z7]] 设为CNN的输入层的数据。则相应的将卷积核设为 [[a1,a2,a3,a4,a5,a6,a7], [b1,b2,b3,b4,b5,b6,b7], [c1,c2,c3,c4,c5,c6,c7]]。 输出值可以根据等式(4)计算得到

(4)

对于图5，3×1卷积用于融合三轴加速度数据。在本节为了进行比较分析，将融合数据的数量设置为3。对有3行n列的数据进行3×1卷积时，会生成形为1行n列的数据。执行n次3×1卷积将会生成n个形为1行n列的数据。将数据融合层的卷积核设为 [[a1],[b1],[c1]],[[a2],[b2],[c2]],[[a3],[b3],[c3]]。 等式(5)中的fd_output为输入数据在经过卷积操作后的输出值，等式中的i=1,2,3

fd_output=xai+ybi+zci

(5)

对数据融合层的每行数据分别进行卷积操作，卷积核的大小为1×7。将卷积层的卷积核设为 [f1,f2,f3,f4,f5,f6,f7]。 其结果由等式(6)计算得到

(6)

比较等式(4)和等式(6)，可以发现等式(6)中多了参数fi， 卷积核大小为1×7则意味着有7个参数f。 因此，等式(6)的输出具有更多的可能性，意味着CNN加入单通道数据融合方法后比不使用数据融合方法的CNN可以提取到更多的有用信息。

3 实验及结果分析

在实验中使用随机梯度下降算法训练活动识别模型。使用10折交叉验证(CV)方法来评估提出的方法。若实验迭代的次数小于375次时，将学习率的大小设置为0.005。若实验迭代的次数超过375次时，将学习率的大小设置为0.001。表1展现了实验设置的参数值。

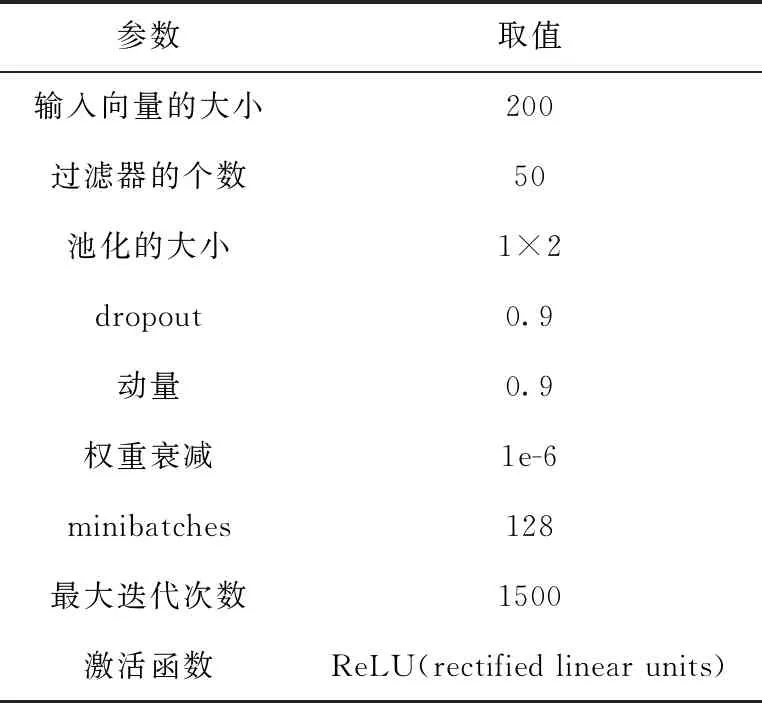
表1 实验的具体参数值

3.1 实验数据集

WISDM Actitracker数据集被用来对本文提出的方法进行测试。该数据集中共有1 098 213个样本，这些样本来自于29个用户。实验数据集中包括走路、慢跑、上楼梯、下楼梯、坐着和站立这6种活动。采样率为20 Hz。

3.2 数据预处理

对原始数据进行标准化是本文预处理数据的方法。Z标准化(zero-mena normalization)利用数据的两个特征值：平均值、标准差来对数据进行预处理，为普遍运用的标准化技术。使用Z标准化处理数据的结果可通过等式(7)计算得到

(7)

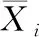
图6 标准化后每个活动的三轴加速度数据

3.3 融合数据数量的影响

在本节中，为了公正地比较模型的准确率，过滤器的个数被设定为50。全部实验中的过滤器个数不再改变。融合数据的多少会对模型的最终结果造成一定的影响。太少的融合数据可能使得其本身不含有充分的有效信息。相反，如果数量太多，可能会导致部分数据冗余并增加参数数量，甚至会出现过拟合或准确率下降的情况。

图7显示了增加融合数据的数量对CNN-DF准确率的影响。当融合数据的数量为1时，模型的准确率为96.36%是曲线的最低点，表明1个融合数据中所含有的有效信息太少。融合数据的数量从1增加到4时，模型的准确率从96.36%增加到98.69%，其中数量从1增加到2时准确率增幅最大。当融合数据的数量为6时，模型的准确率为98.80%是曲线的最高点。融合数据的数量从6增加到10时，曲线略微波动下降，最终下降至98.58%。融合数据的数量的连续增加不一定会导致准确率的增加，但会增加参数的数量，这可能导致过拟合。

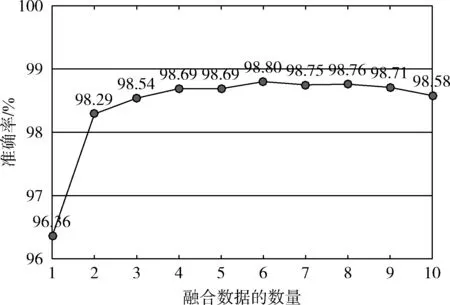
图7 拥有不同数量融合数据的模型准确率的比较

3.4 与CNN的比较

基于数据融合的CNN方法是在CNN之前加了数据融合阶段，那么将该方法与CNN进行比较，可以判断数据融合阶段对模型的分类准确率是否有影响。本节对CNN和CNN-DF从两点进行比较：准确率和不同数量的训练数据对模型准确率的影响。

CNN和CNN-DF两个模型的准确率见表2。从表2中可以看出，使用单通道数据融合方法的CNN-DF准确率达到98.80%，比CNN的准确率98.60%高0.20个百分点。CNN-DF和CNN中均使用了考虑到空间依赖性的二维卷积核，因此CNN-DF准确率的提高是由于使用了包含轴之间相关性的融合数据。

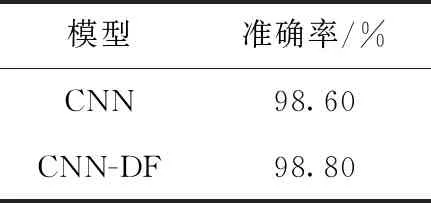
表2 模型的准确率比较

不同数量的训练数据对模型准确率的影响如图8所示。在图8中，CNN-DF的曲线保持在CNN的曲线之上，无论训练数据的数量是多少，CNN-DF的准确率始终比CNN的准确率高。结果表明，使用单通道数据融合方法能够提高模型的准确率。

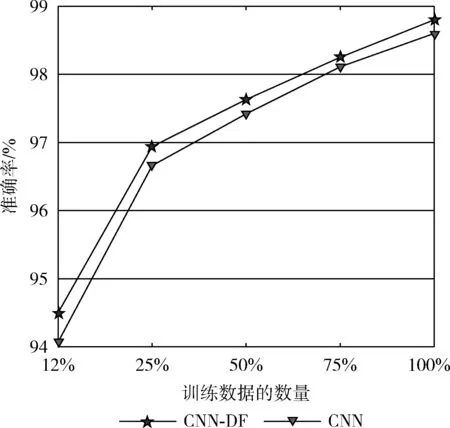
图8 模型在不同数量训练数据情况下的准确率的比较

3.5 与现有方法的准确率比较

为了验证提出的方法的有效性，本文将其与一些现有方法进行比较。结果见表3。在文献[11]中一种分类器方法集合即J48、逻辑回归和多层感知器算法的集合被提出，通过实验验证了该方法与上述3种算法相比其性能更好。文献[12]中的结果表明，深模型可以有效地提高准确率，而不需要对特征进行手工设计。在文献[13]中发现资源限制和简单的设计方法可能使得浅层特征比通过深度学习方法提取到的特征具有更强的判别性。文献[13]的作者提出将浅层特征和深度学习特征相结合并与仅使用深度特征的文献[14]中的方法对比，发现两种特征相结合的方法的准确率更高达到了98.60%。CNN-DF不是根据人类领域知识去手动的提取特征，而是使用CNN进行特征提取和分类，这与上述方法不同。

表3 提出的方法与现有方法的比较

表3通过与现有方法进行比较，发现基于数据融合的CNN方法将准确率提高了0.20个百分点。提出的方法实现了最高准确率，这表明它是解决HAR问题的有效方法。

图9为提出的方法的分类结果。将CNN-DF与表3中准确率最高的方法进行对比。表4展现了CNN-DF与Ravì et al[13]的活动的分类结果，表中的最后一行是两种方法之间的准确率差值。该准确率差值清楚地表明了哪种方法实现了更高的准确率，哪种活动的准确率提高得更明显。观察表4能够看出坐着和站立的准确率提高的最多，分别为1.49%和1.43%。对于下楼梯，提出的方法的准确率达到了95.51%，相较Ravì et al[13]提高了1.07%。而对于慢跑、上楼梯和走路来说，这3种活动的准确率提升幅度较小仅为0.12%、0.20%和0.16%。观察图6能够看出站着和坐立的3条曲线较为独立相交部分较少。慢跑、走路和上楼梯的3条曲线在图中相交部分较多，数据的分布较为密集。当活动的x轴、y轴和z轴曲线相交部分较少即数据的差异较明显时，其识别准确率将有明显提高；而当活动的x轴、y轴和z轴曲线相交部分较多时，其识别准确率仅有小幅提升。本文提出的CNN-DF适用于解决人体活动识别问题，更适用于解决三轴加速度数据差异较大的活动识别问题。

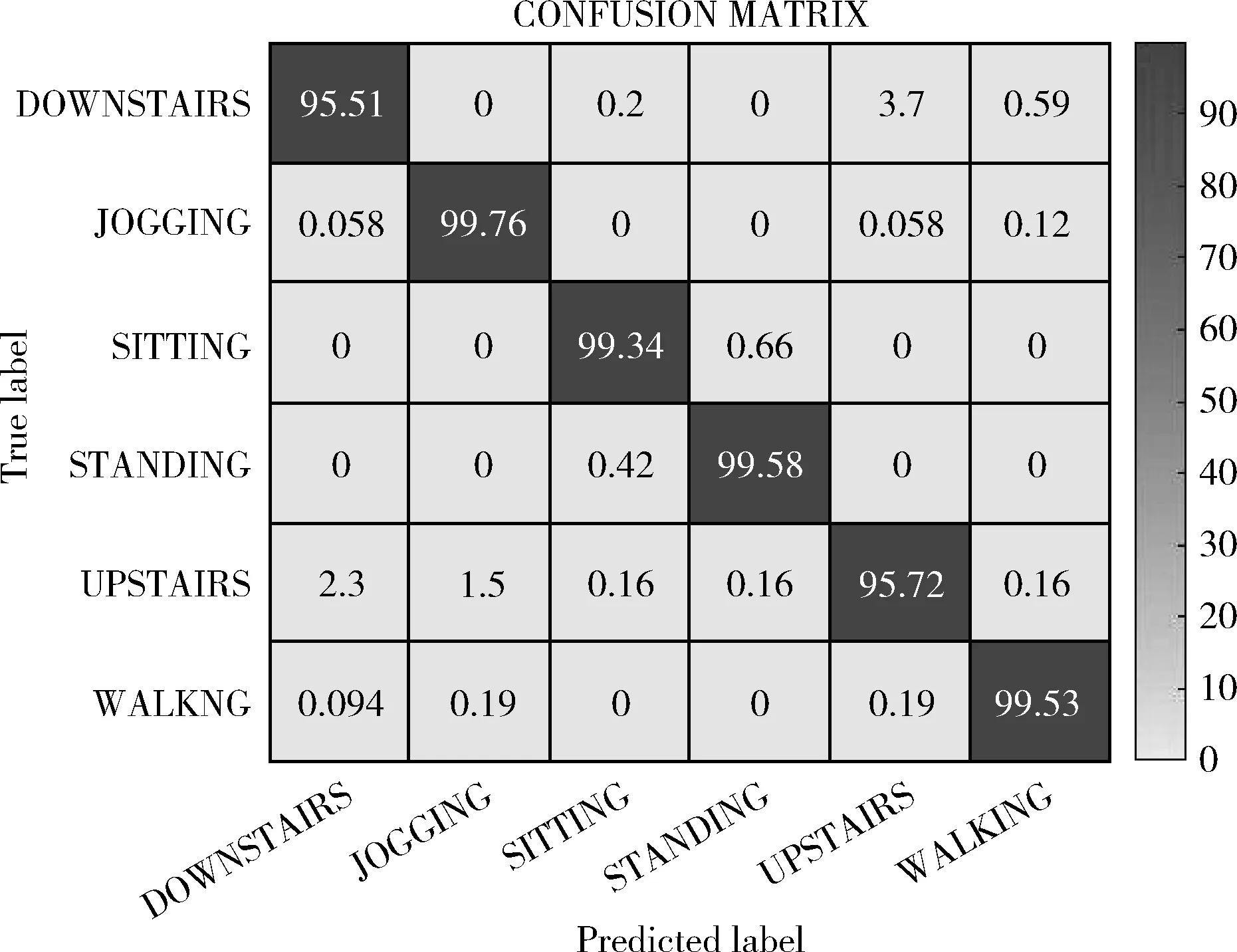
图9 提出的方法的混淆矩阵

表4 提出的方法与表3中准确率最高的方法的比较

4 结束语

在本文中，我们提出了一种基于数据融合的CNN方法，主要包括两个阶段，数据融合阶段和CNN阶段。所提出的方法旨在充分利用传感器内轴之间的相关性来提高模型的准确率。结果表明提出的方法是有效的，该方法的准确率高于CNN的准确率。进一步分析该方法可以发现其适用于解决三轴数据差异较大的活动识别问题。本文研究了在使用单一传感器的情况下如何通过借助轴之间的相关性来对模型的准确率做出改善。在更加复杂的应用场景下如何同时使用多个传感器，如何更好地利用轴之间的相关性仍是一个值得探索的问题。