基于CUDA的多信道锋电位实时分类方法

蔡瑞初，赵坤垚+，黄礼泊，何 炯，陈 瑶,4

(1.广东工业大学 计算机学院，广东 广州 510006；2.广东工业大学 信息工程学院， 广东 广州 510006；3.阿里巴巴达摩院 数据库与存储实验室，新加坡 068811; 4.新加坡高等数字科学中心，新加坡 138602)

0 引 言

在神经科学研究中，根据神经元的电位信息来研究神经元的编码机制、分析神经元的协同行为是神经科学、生物医学和计算机科学等交叉领域科学家使用的基本方法[1]。新型高密度电极探针[2]可同时记录数百个密集间隔位点的采集波形，每个位点记录的波形包含由神经元的位置和生理特征等组成的特定信息，将电极探针插入到大脑中并记录电极尖端周围的局部电位活动，被观察到的神经元的动作电位称为锋电位[3]。由于不同的神经元产生的锋电位不同，对采集到的锋电位进行提取并将其分配给所属神经元的过程，称为锋电位分类[3,4]。

当前，锋电位分类主要分为低维信道锋电位分类和高维信道锋电位分类。针对低维信道分类任务，文献[5]基于四元数的波形特征提取和文献[5]利用GMM算法去自适应分类的方法，都达到了很高的分类准确率，但是两种方法都是针对低维信道数据，数据的采样信道为单信道或者四信道，不能推广到高维锋电位数据的实时分类应用中。随着高维探针技术的快速发展，记录的高维锋电位数据提供了更多可用于分类的信息，文献[7]提出的Masked GMM算法，针对GMM算法进行改进，使得高维信道数据的计算时间大大缩短，同时也达到了很高的分类准确率，但是其分类算法运行时间过长，影响实时分类场景的应用；文献[8]提出的基于空间和形状的聚类算法和文献[9]提出的ISO-SPLIT技术，在高维锋电位数据的分类准确度和算法执行效率方面都有很好的表现，且都达到了实时分类，但是两个算法分别需要在12个和20个CPU内核的工作站上运行，对硬件资源要求较高；文献[10]采用模板匹配算法并在单GPU上进行了加速，达到了实时分类要求，但是模板匹配方法在锋电位分类应用方面的理论目前还不完善[3]，模板的生成方法对分类结果影响很大。

基于上述情况，本文提出了基于CUDA的特征掩蔽高斯混合模型，一方面，该模型基于高斯混合模型改进得到，具有很好的抗噪性能，在锋电位分类中达到了很高的分类精度[7]；另一方面，该模型整个算法流程在CUDA架构下进行并行实现并优化，大大减少了算法运行时间，同时该算法设计部署在单GPU上，对硬件要求较低。与文献[7]相比，本文的并行实现方案在32信道锋电位数据集上，确保分类准确率的同时，实现了170倍的加速，实现了锋电位的实时分类。

1 背景技术

1.1 特征掩蔽高斯混合模型

特征掩蔽高斯混合模型(Masked GMM)是由Kadir SN，Goodman DFM等提出来的[11]，该模型主要针对高维聚类分析中存在的样本特征维度高，从而导致的高斯混合模型出现“维度灾难”和迭代计算效率低的问题，对于样本中部分不重要的特征通过设定特征阈值进行掩蔽，生成掩蔽向量，掩蔽的特征假设为噪声且其服从高斯分布，之后将噪声和未被掩蔽的特征根据掩蔽向量拟合为新的输入数据，在之后的迭代更新过程中，对于掩蔽特征的更新可以根据噪声的均值和方差直接得到，从而达到降低计算量的目的，并极大减少了模型中间运算过程的数据存储空间，因此该算法非常适合高维信道锋电位数据等高维稀疏数据的聚类。

该算法主要包括下面6个步骤。

(1)掩蔽向量的生成：训练样本集X=[x1,x2,…,xn]T， 样本数为N， 维数为D， 其中Xi=(xi,1,xi,2,…,xi,D)T,xn,i表示第n个样本点xn的第i个特征。对于所有样本点的每个特征计算其标准差SD， 同时设置高低阈值的系数α与β， 用mn,i表示xn,i的掩蔽向量，mn,i表示如下

(1)

通过掩蔽向量，对于所有样本的每个特征i， 计算该特征的掩蔽向量为0的特征的均值vi和方差σi2。

(2)使用掩蔽向量重构原始数据集：对于原始数据集，需要根据掩蔽向量将其拟合为噪声和真实特征的混合特征，由式(1)可知掩蔽向量mn,i为[0,1]区间的值，所以将mn,i作为第i个特征的原始数据分量的权重，将1-mn,i作为第i个特征的噪声分量的权重，可以计算得到重构数据集Y， 同时也可以得到重构数据集的特征方差η， 重构数据集每个特征yn,i和每个特征的方差ηn,i的计算公式如下

yn,i=mn,ixn,i+(1-mn,i)vi

(2)

zn.i=mn,i(xn,i)2+(1-mn,i)(vi2+σi2)

(3)

ηn,i=zn,i-(yn,i)2

(4)

其中，zn,i表示原始数据集的平方通过掩蔽向量拟合后的期望，用于计算特征方差。

(3)M步：计算簇的权重、均值与协方差：高斯混合模型通常通过期望最大化算法进行参数求解，对于特征掩蔽的高斯混合模型，由于掩蔽向量的存在，对于簇k更新权重ωk、 特征均值μk和协方差∑k的公式如下

(5)

(6)

(7)

其中，Ck表示簇k中样本点的集合， |Ck| 表示第k个簇中样本点的个数，Mk,i表示第k个簇的第i个特征被掩蔽的样本点的集合，从式(6)、式(7)可以看到，对于μk和∑k的更新，分为掩蔽特征和非掩蔽特征进行更新，掩蔽特征的更新可以通过噪声均值和方差直接得到。对于锋电位分类任务，锋电位的非掩蔽特征数量很少，因此大大降低了存储空间和计算复杂度。

(4)E步：计算每个样本点的对数似然估计：通过上述步骤(3)的计算结果,可以得到第n个样本点属于簇k的对数似然估计πn,k

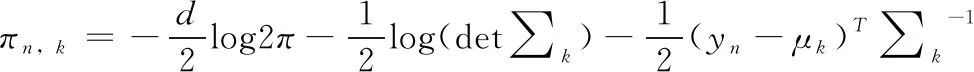
(8)

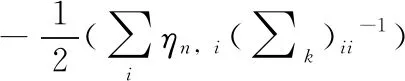
(5)评估聚类结果并重新分配簇：由于特征掩蔽高斯混合模型在迭代过程中自动确定高斯混合中的聚类数量，因此需要引入惩罚函数，该函数通过抑制具有大量参数的模型来惩罚过拟合。本文采用贝叶斯信息准则(BIC)

BIC=κln(N)-2ln(L)

(9)

其中，κ为模型中的自由参数，L为被评估模型的最大似然，N为样本点数量。对于特征掩蔽高斯混合模型，若一个簇中有γ个未被掩蔽的特征，那么该簇的自由参数数量F(γ) 为

(10)

因此对于有K个簇的掩蔽高斯混合模型，自由参数κ表示如下

(11)

通过式(8)计算出的πn，k， 将每个样本点重新分配到似然函数最大的簇中。对于重新分配后的所有簇，其得分S为

(12)

当得分S的变化值小于设定的阈值则结束迭代。

(6)簇的删除和分裂：算法在初始时给定一个可能的最大的簇数量，之后在M步和E步迭代过程中，通过判断当前簇是否满足分裂或删除的条件，动态调整簇的数量。对于当前的每个簇，如果将其中的样本点重新分配到对数似然次大的簇中，聚类评估结果更优，则将聚类评估结果最优的簇删除，其中的样本点重新分配到对数似然次大的簇中。同样的，对于当前的每个簇，通过M步和E步将其分裂为两个新簇，并评估聚类结果，如果聚类评估结果更优，则将评估结果最优的那个簇重新分裂为两个簇。

由于该模型通过EM算法迭代求解，所以模型的主要运行时间花费在(3)(4)(5)(6)这4个步骤上，因此加快每一轮迭代的计算时间对于实时性的实现极为重要。

1.2 CUDA统一设备计算架构

CPU具有复杂的控制逻辑和大容量的缓存，适合进行事务管理，处理分支繁杂的任务，而GPU专为计算密集型、高度并行化的计算而设计[12]。在NVIDIA公司推出的CUDA编程模型下，使用简单且易实现的扩展C语言就能编写GPU并行程序，大大提高了GPU的可编程性。CUDA 架构模型[13]如图1所示，CUDA利用向量将线程组织成为3个不同的层次：线程、线程块以及线程网格。每个线程都有唯一的线程编号；每个线程都有一个容量较小但速度快的私有寄存器；每个线程块则拥有一个共享存储器，该存储器对块内的所有线程均可见；网格内的所有线程都可读写一块相同的全局存储器和一个只供读取的常数存储器与纹理存储器。CUDA的主要运算库包括CUBLAS、CUSOLVER和THRUST等，这些库能解决典型的大规模并行计算问题，开发人员在运算库的基础上可以快速、方便地建立起自己的计算应用。

图1 CUDA架构模型

2 基于CUDA的并行Masked GMM算法

通过第一小节介绍的特征掩蔽高斯混合模型和CUDA统一设备计算架构，本节针对特征掩蔽高斯混合模型的并行性及其优化进行分析。

2.1 Masked GMM算法的并行性分析

针对GMM算法，文献[14]已经进行了基础的分析和实验，但是其并没有进行算法并行分析和优化，下面针对应用于高维稀疏脑电波数据的Masked GMM算法的每个步骤进行并行性分析，并根据分析做相应的实现优化。

(1)对于掩蔽向量的计算,首先对于每个特征的标准差的计算相互独立，可以并行计算，通过得到的SDi， 更新特征阈值，对于xn,i， 通过式(1)可知其计算也可以并行执行，因此对于每个xn,i分配一个线程去计算该特征的掩蔽向量mn,i， 同样对于每个特征的噪声的均值和方差的计算也采用线程编号和特征编号对应的方式并行执行计算。

(2)对于原始数据集的重构，由式(2)、式(3)、式(4)可以得到，每个被重构的特征点只和原始特征点的数据信息有关，而与其它的特征点无关，特征点可以和线程块中的线程一一对应，使得重构计算可以并行执行。

(3)在聚类开始之前，我们需要初始化锋电位的初始簇编号，在锋电位分类的应用中，我们无法提前确定簇的个数，相比K-means的迭代初始化方法，本文通过两个锋电位的掩蔽向量的海明距离度量两个锋电位的相似性，相近的锋电位初始化为一个簇。对于任意锋电位，其和已知簇中锋电位的掩蔽向量的海明距离可以并行计算，从而避免K-means迭代初始化耗费大量时间。

(4)在聚类迭代过程中，通过M步中的式(5)、式(6)、式(7)，可知对于每个簇的权重，均值和协方差的计算只与当前的簇中的锋电位有关，因此簇与簇之间的M步计算是独立的，可以并行执行，同样的对于E步式(8)中对数似然的计算，也以簇为更新的单位，同样可以并行执行。

(5)根据对数似然值重新分配簇，需要快速得到每个锋电位的最大对数似然值，同时快速计算每个簇所有锋电位最大似然值的和，可以利用CUDA常用的规约算法进行并行查找最大似然的簇，同时利用规约算法求得所有锋电位的最大似然的和，并行更新得分。

(6)对于删除步骤，由于对当前存在的每个簇都尝试删除并计算得分，最后选取得分最低且低于当前不删除簇的情况下的得分，所以可以并行尝试删除每个簇，并计算得分，最后再判断是否删除并进行并行更新。同理对于簇的分裂步骤，也并行尝试分裂每个簇，对于分裂过程中的M步和E步的调用，在上面(4)中已经分析可以并行执行。

综上，Masked GMM算法中的各个步骤都可以并行执行，适合在GPU上进行实现。

2.2 并行Masked GMM算法的优化分析

2.2.1 GPU中数据存储与访问优化

(1)锋电位数据传输进GPU端进行存储时按照列优先的方式，这样每个线程对每个数据点的特征访问可以达到合并访存，减少内存访问的次数，从而减少访问内存的时间；

(2)对于噪声的均值v、 方差μ以及E步和M步迭代更新过程中的簇的均值、协方差和似然估计值等，由于其数据量较小，可以放进共享内存中，加快线程对其访问速度；

(3)由于Mask GMM算法迭代过程中临时变量很多，每次迭代进行分配和释放临时变量会带来巨大时间开销，因此对于临时变量，分配为全局变量，在程序整个运行过程中，只分配和释放一次，减少内存分配的时间开销。

2.2.2 算法的执行流程优化

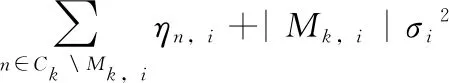
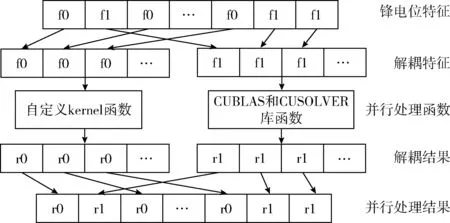
图2 特征解耦优化

(2)在GPU端的未优化实现中，并行执行完M步的簇权重、均值和协方差等的更新，将结果储存于全局存储器，用于E步所有簇的更新，在GPU端的优化实现中，当M步并行更新完一个簇的权重，均值和协方差之后，直接对该簇进行E步的对数似然估计的更新，流程优化如图3所示，这样一方面可以避免中间结果的巨大存储空间的分配，另一方面将对全局内存的访问转化为对共享内存或寄存器的访问，减少访问内存的开销。

图3 处理流程优化

(3)由于在M步和E步的迭代更新过程中，每个簇的参数更新是独立的，因此我们采用CUDA stream技术，如图4所示，其中Copy Engine负责数据的传输控制，Kernel Engine负责数据的并行计算，在一个CUDA stream中可以保证运算按既定的顺序执行，在不同的stream中的运算可以交叠执行，这样一方面增加了运行的并行性，另一方面可以很好隐藏数据传输。

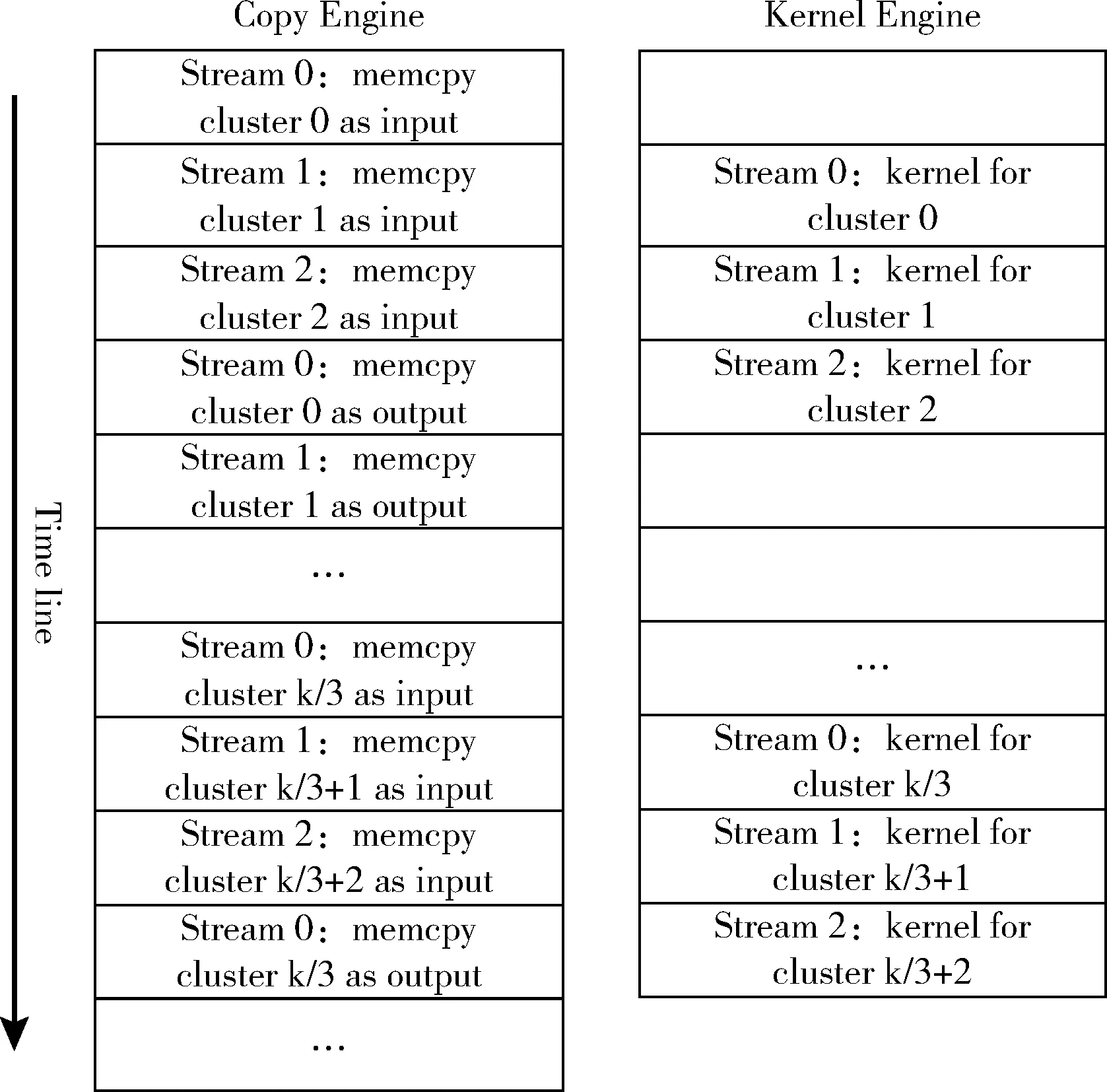
图4 CUDA stream 优化

2.2.3 默认参数的优化

由于Masked GMM算法的初始簇为一个比较大的值，默认为500，通过不停的迭代去删除簇，从而达到最终簇的数目，通过式(6)、式(7)、式(8)可以看到其更新的计算量和当前存在的簇的数量有很大的关系，所以可以在启发式的初始化过程中将簇的数量初始化为一个较小的值，该值随着初始锋电位的数目动态设定，初始锋电位数量越多，该值越大，然后执行迭代，这样一方面可以减小初始存储空间的分配，另一方面大大加速算法的收敛速度，减少了计算时间。通过实验，在不影响分类精度的情况下，算法的参数优化达到了10倍左右的加速。

3 实验结果和分析

3.1 实验平台和实验数据集

为了验证基于CUDA加速的Masked GMM算法的性能，本文使用两个32信道的锋电位数据集进行实验，数据集1在文献[7]中使用，是由已知的睡眠大鼠的前卤躯体感觉皮层锋电位数据混合而成，数据集2是Kampff实验室的公开数据集，是由麻醉大鼠的初级运动皮质(M1)和海马CA1中记录得到。本文将每个数据集切分为10 s，30 s，60 s和120 s的4个子数据集分别进行实验，并与CPU端的串行实现进行对比评估算法准确性和加速比。

实验参数设置为：CUDA stream数量为3，初始簇的数量为500，参数优化后的初始簇数量为50，高阈值系数β为4.5，低阈值系数α为2.0，最大迭代次数为1000，改变所属簇的锋电位数量阈值为0.05，得分改变阈值为0.01，算法迭代结束的条件为下列情形之一：①算法运行超过最大迭代次数1000；②算法在该轮改变所属簇的锋电位数量小于总锋电位数量*0.05；③算法两轮迭代得分差值小于0.01。

实验所采用的计算平台见表1。

表1 计算平台

实验所采用的数据集锋电位数量见表2。

表2 数据集中的锋电位数目

3.2 实验结果对比

3.2.1 迭代误差评估

由于GPU和CPU计算精度的不同，因此Masked GMM算法在GPU端和CPU端运行结果会产生误差，为了估计不同平台代码的运行误差，这里分别对两个数据集的30 s的子数据集的前5次迭代每个簇的权重、均值和方差的相对误差均值进行评估，评估代码为CPU端代码和未进行参数优化的GPU端代码，结果见表3。

由表3可知，算法在30 s子数据集上的前5次迭代的权重、均值和方差的最大相对误差为0.000 05，算法的平均运行误差在锋电位分类任务中是可以接受的，也说明了算法流程的执行准确性。

表3 相对误差估计

3.2.2 聚类结果评估

为了评估并行Masked GMM算法的最终聚类结果的正确性，将GPU端与CPU端的聚类结果进行比较，同时GPU端代码根据初始参数的不同，会产生两个对比结果，其中GPU默认参数中初始聚类数目为500，优化后的默认参数中初始聚类数目为50，其它参数不变，同时关于CPU与GPU之间聚类结果的比较采用了文献[9]的对比方法，主要对比两种方法的主要的簇的数量和簇中波形的匹配。数据集1结果见表4，数据集2结果见表5。

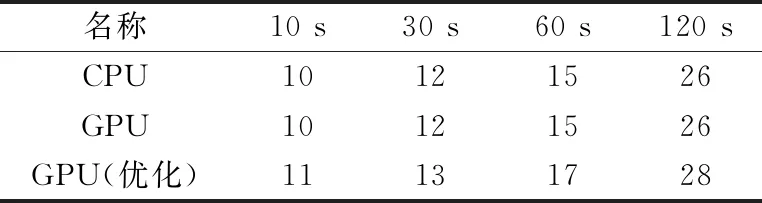
表4 数据集1聚类数量评估

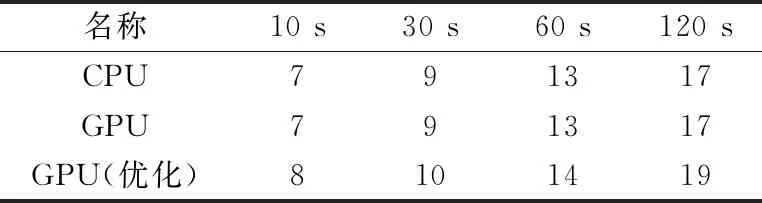
表5 数据集2聚类数量评估

通过表4和表5，可以看到在数据集1和数据集2上，未进行参数优化的GPU端代码和CPU端代码的最终聚类数目完全一致，同时对于参数优化的GPU代码，通过匈牙利算法对优化后的GPU代码的每个簇中的锋电位和CPU代码的每个簇中的锋电位进行最大匹配，得到GPU端的多出来的簇是CPU端的某个簇分裂出来的，这在算法中是可以容忍的，因为在人工校验阶段会由人工去分裂或者合并聚类结果中的相似簇[7-10]。

3.2.3 运行时间评估

为了评估并行Masked GMM算法的加速效果，我们分别在两个数据集的8个子集上运行CPU端和GPU端的代码，由于参数优化后的GPU端代码并不影响聚类结果的准确性，因此这里GPU端为初始簇数量为50的实验结果，数据集1的加速比见表6，数据集2的加速比见表7。

由表6和表7可知，在数据集1中，GPU端的运行时间相对于CPU端，最大加速比达到了173倍，在数据集2中，GPU端的运行时间相对于CPU端，最大加速比达到了160倍，同时在两个数据集中，GPU端运行时间均少于数据采集时长，达到了锋电位数据的实时分类。

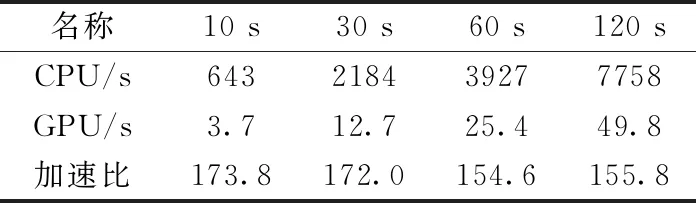
表6 数据集1加速比评估

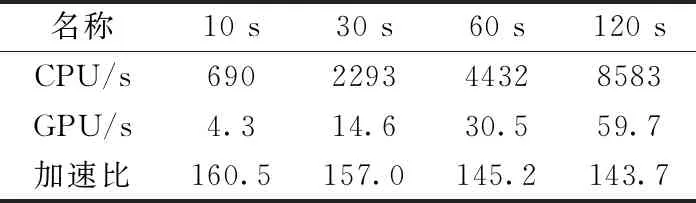
表7 数据集2加速比评估

4 结束语

本文提出了一种基于CUDA的多信道锋电位实时分类方法。该方法针对高维信道神经元锋电位数据高维稀疏的特性，对Masked GMM模型在单GPU设备上进行并行实现，同时根据锋电位数据的特征和算法的处理流程进行优化，最终在保证分类精度的情况下，实现了锋电位的实时分类，并降低了实时分类运算所需的设备要求。实验结果表明，在32信道的锋电位数据集上，基于CUDA的多信道锋电位实时分类方法相比于文献[7]的CPU串行实现，达到了最高170倍的加速，同时算法的运行达到了实时，极大地方便了科学研究和实际应用，同时，本文的算法具有很大的扩展性，随着锋电位数据量的增加，可以考虑将算法改进为增量式聚类，使得算法可以在当前硬件设备上运行更大的锋电位数据并实时分类。