基于核模糊粗糙集的高光谱波段选择算法
张 伍,陈红梅
(西南交通大学 信息科学与技术学院,成都 611756)
0 引言
多光谱或高光谱图像是20世纪80年代兴起的遥感空间技术,通过搭载不同平台的传感器,能在连续紧密的光谱波波段上对目标同时成像。高光谱数据是一个图像立方体,它的前两个维度代表图像的空间位置,第三个维度代表图像的波段,所以它的每一个像元是一条连续的光谱曲线,通过分析光谱曲线的特点,可以得到像素点所代表的地物真值对象。也可以把像元看成一个模式,它的属性值等于对应波段上的辐射亮度值。高光谱图像因为含有很大的信息量,使其在多种应用(医学、农作生产、矿物勘探等)方面具有很大的价值,但因波段之间具有较高的冗余,所以存在存储空间消耗大、计算时间长、图像分类时可能存在“HUGHES”问题[1];因而需要对高光谱图像进行处理,降低它的维度并且同时保留较高的地物分类的能力。
高光谱降维技术分为特征选择以及特征提取。在特征提取中,经过一系列数学的变换,可将原来的所有波段数据压缩为新的数据以代替原来的数据集,如主成分分析[2]、独立成分分析[3]、局部线性嵌入[4]等。基于变换的降维方式,其优点是可以经过若干变换直接将高维数据减少到几维甚至一维,降维后会缩短数据进一步分析处理时间。缺点是对图像进行了变换,改变了图像原有的特性,使一个特征下的值无法还原成为对应的图像中的值。高光谱波段选择是指从原始数据集中挑选出一些未经变换过的波段图像组成高光谱图像子集,并尽可能反映原始高光谱图像的特性。高光谱图像波段选择不会破坏原本图像本身的物理属性,其结果解释性更强。
根据是否使用地物真值信息,高光谱图像波段选择算法又分为无监督波段选择算法和有监督波段选择算法。Liu等[5]基于邻域粗糙集理论进行高光谱波段选择,并分析了算法的稳定性;Patra等[6]用粗糙集理论计算每个光谱波段的相关性和重要度,定义了一个新的准则用来选择有效的波段;Guo等[7]根据真实地物真值表与波段图像间的互信息进行高光谱波段选择。这些方法进行高光谱波段选择时,需要依靠地物真值信息表,是有监督波段选择方法。刘春红等[8]提出了通过计算高光谱信息含量以及与前后波段相似度之和的比值,进行优先度排序的自适应波段选择算法。学者们提出的使用相对熵作为衡量波段信息含量的最大信息量方法[9]、基于选取聚类中代表波段的方法[10-11]则属于无监督波段选择方法,它们不需要地物真值信息,直接进行波段图像选取。
本文提出了一种基于核模糊粗糙集理论的有监督高光谱波段选择算法。它考虑波段像素类分布,定义一种新的度量方式。算法同时考虑波段相似性及波段信息熵选择波段,直至达到预先设定的波段个数。这种方式产生的波段子集波段间冗余小,且信息含量大。本文算法与相关波段选择算法进行了比较,具有较好的效果。
1 核模糊粗糙集基本概念
经典粗糙集理论是一种分析不精确和不确定信息的数学范式,它能够在不损失有效信息的情况下获得数据核心知识,对数据进行约简,实现数据的分类和预测;然而,在实际应用中,对象属性值可能是模糊的或者是数值型的,它们间的关系不能如经典粗糙集中通过等价关系进行判断。因而Dubois和Prade提出了模糊粗糙集理论,推广了经典粗糙集。
定义1[12]设U是论域,A:U→ [0,1],则称A是U上的一个模糊集合,A(x)称为模糊集合A的隶属函数。对∀x∈U,A(x)表示x隶属于模糊集合A的程度,简称为隶属度。U上全体模糊集合的类称为U的模糊幂集,用F(U)表示,A∈F(U)意指A是U上的一个模糊集合。
定义2[13]设U,V为两个论域,当满足R∈F(U×V)时,则称R为U到V的一个模糊关系,隶属度R(u,v)称为(u,v)∈(U×V)关于R的相关程度。
定义3[12]设U是有限论域,U≠∅,且R∈F(U×V),若x,y,z∈U满足:
自反性:R(x,x)=1;
对称性:R(x,y)=R(y,x);
min-max传递性:min(R(x,y),R(y,z))≤R(x,z);
则称R是模糊等价关系。
定义4[13]设R为论域U上的一个模糊等价关系,A是U的一个模糊子集,模糊粗糙集的上近似集以及下近似集定义为:
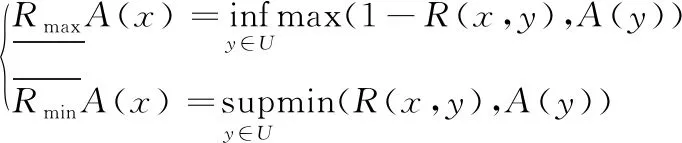
定义5[15]给出一个非空有限论域U,如果一个实值函数k:U×U→R,是对称且半正定的,称它为核函数。

4)圆核:

5)球核:
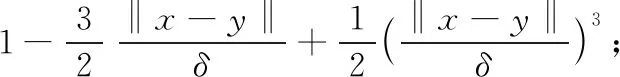
‖x-y‖<δ
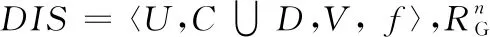
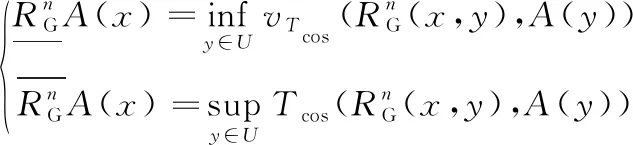
其中:
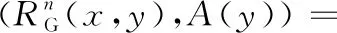
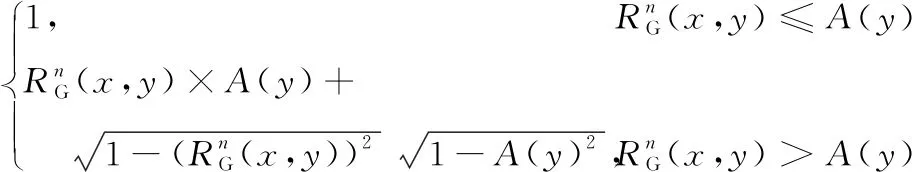
定义7[17]给定决策系统DIS=〈U,C∪D,V,f〉,RG是论域U上的高斯核模糊等价关系。U被决策属性划分为{d1,d2,…,dn},那么D对B⊆C的模糊正域定义如下:
定义8[17]给定决策系统DIS=〈U,C∪D,V,f〉,RG是论域U上的核模糊等价关系。U被决策属性划分为{d1,d2,…,dn},那么D对B⊆C的属性依赖度定义如下:
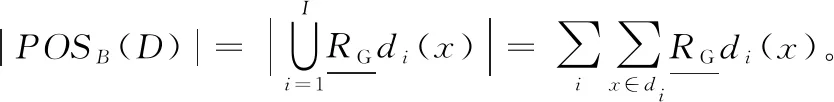
2 提出的算法
本文提出了基于核模糊粗糙集(Fuzzy Rough Set, FRS)的高光谱波段选择算法。它能在获得有效地物信息时,确定波段间的相似性。算法采用最大相关性最大重要度的搜索策略对高光谱图像进行波段选择,这样既考虑了波段间相似性又考虑了波段图像信息含量。
2.1 基于核模糊粗糙集相似性度量
皮尔逊系数是一种常用的相似性度量方式。皮尔逊系数计算波段i与波段j间的相似性公式如下:
(1)
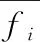
根据去除水汽污染的Indian Pines数据集为例,计算它的波段相似度矩阵,并将其可视化,如图1所示。
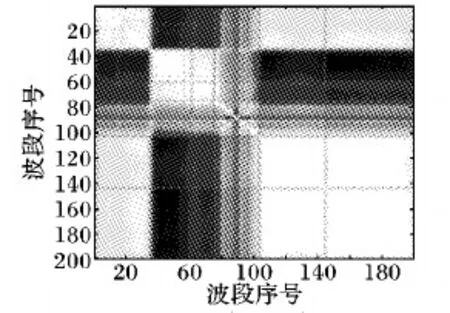
图1 相关性矩阵Fig. 1 Correlation matrix
在高光谱图像中,波段值表示场景对不同波长电磁的反射率。从物理角度来看,波长较近的电磁波产生相似的反射率。图1是由图像的灰度来画出来的。根据灰度图像的亮度特点可以知道,亮度越高相似性越大,亮度越暗相似度越低。从图1中可以发现对角线区域的亮度一直很高,因此可以说明相邻近的波段之间相似性较强,但是当有时候能获得地物真值信息的情况下,皮尔逊系数并不能利用地物真值信息。粗糙集能有效地分析不确定信息,而高光谱图像相邻波段之间相似性较强,因此本文引入核模糊粗糙集定义了一种新的高光谱波段图像间的相似性度量。
设U={x1,x2,…,xn}是高光谱图像n个像元的集合,B={b1,b2,…,bm}为高光谱数据的m个波段的集合,这些像元以及波段组成了一个表T。T={wij|i=1,2,…,n,j=1,2,…,m},这里wij代表的是xi像元在波段bj下对应辐射亮度值。设D为一个决策属性集,其包含像元xi∈U的类标签,B为条件属性集,因此,根据粗糙集理论,一个高光谱数据集可以用一个决策表T=(U,B∪D)表示。
根据定义8,可以求得波段bj与决策属性D之间的属性依赖度,以及波段bi与决策属性D之间的依赖度,如果它们值大小接近,可以近似说明bi以及bj较为接近,但是这样有可能不够细化,因为虽然每个波段下像素的属性下近似总和一致,但是分布情况有较大差异时,仍然具有较高的相似性。
故采用分别计算波段bi中每个像素与其决策属性的下近似减去波段bj对应像素的下近似的差值取绝对值,把所有像素对应绝对值求和,代表波段bi以及波段bj之间的广义距离。定义波段bi以及波段波段bj之间的距离公式如下:
(2)
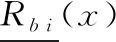
故本文取式(2)的值的倒数作为相似性度量。
假设高光谱图像数据集中有L个波段,可以计算出一个L×L的波段相关性矩阵。波段相关性矩阵可以被表示如下:
(3)
这里C表示所有波段之间的相关性,ci, j表示第i个波段以及第j个波段之间的相关性。ci, j值越大,波段i以及波段j之间的相关性越大。
2.2 信息熵
高光谱波段选择算法旨在选择出信息量大且冗余小的波段子集。如果只考虑相关性则可能会忽略掉一些信息含量较大的波段。本文提出的核模糊粗糙集波段选择算法把波段信息含量也纳入了考量范围。
根据香农的信息理论,信息熵被用来衡量不确定信息的信息含量。假设A是一个随机变量,a是它每一种可能的值。a的分布概率用PA(a)表示。信息熵定义如下:
(4)
一些方法直接使用信息熵作为一个评价标准在波段选择中。在这些方法中,信息熵被用来衡量各个波段的信息含量,然后根据大小进行排序,之后选择信息熵大的那些波段,但是这样会出现冗余的情况,可能两个波段虽然信息量都很大,但是它们比较类似,对之后的分类精度并没有很大提高。
图2显示了离散化之后计算的数据集Indian Pines中一个波段的信息熵变化曲线。
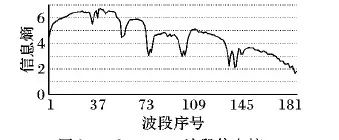
图2 Indian Pines波段信息熵Fig. 2 Entropy of Indian Pines band
从图2中可以看出每一个波段所对应的信息熵即信息含量的大小,相邻波段之间的信息熵在大多数情况下非常接近。
2.3 最大相关性最大重要度搜索策略
Zhang等[18]提出的波段相关性分析(Band Correlation Analysis, BCA)算法采用了最大相关性的思路,每次只挑选一个波段。假设准备从全部波段L中选取n个波段,并且已经选择了m个波段,正准备去选择第m+1个波段。对于每一个待选择的波段,当前波段可以分为两个集合,一个是已经选择了波段集合ΦS以及剩余未选选择的波段集合ΦU,它们分别具有m,L-m-1个元素在集合内。波段i的代表能力可以用式(5)计算:
(5)
Su(i)表示波段i与其他剩余未选择波段之间的平均相似性。它的值越大,它越能代表其他波段。对于波段i的冗余部分用式(6)表达:
(6)
它的值越小,冗余相对应地也越小。
因此,在剩余未选择波段中,可以把上述两者结合起来,并根据信息熵选取选择第m+1个波段。如式(7)所示:
S(i)=(Su(i)-Ss(i))×H(i)
(7)
然后每一次在剩余波段中计算S(i),把值最大的波段添加进来,更新已选择波段。
FRS算法流程如下所示。
1)
输入s=∅,B={b1,b2,…,bl},目标选择的波段数n。
2)
根据式(2),计算每个波段与其他波段的相关性。生成相关性矩阵。
3)
重复下述3个步骤直至选择好预定的波段数。
4)
使用式(7),计算每一个在B中剩余波段的排序值。
5)
选择bj∈B产生最大值的那个波段。
6)
更新S={s,bj},B={B-bj}。
S即为波段选择结果。
3 实验及结果分析
3.1 实验数据集
为了验证本文提出的FRS波段选择算法的可行性与有效性,本文下载了Indian Pines数据集。
数据集大概有一半的像素点为无法标记的地物,它的地物真值分布不均匀,从几十个到两千余个不等。Indian Pines数据集采用的是机载成像光谱仪AVIRIS于1992年6月于美国印第安纳州所拍摄。该图像大小为145×145像素,其空间分辨率为25 m,光谱分辨率为10 nm,波长范围0.4~2.5 μm,对应的波段数为220个。目前,国内外高光谱遥感数据的降维以及分类实验都广泛采用此数据进行仿真实验分析。美国普度大学曾针对该地区给出一份实地考察报告。区域主要位于印第安纳州的西北方向。该区域内主要被各种蔬菜和天然植被覆盖,蔬菜主要为玉米、大豆、小麦等,天然植被主要为干草、森林、草地等。除此之外,还有一些是高速公路和铁路,以及一座无线电发射塔和房屋等人工用地。数据中还有一些无法区分的具体类别的像素点以编号0表示。
此外,移除了20个水汽污染波段以及15个噪声波段,用剩余的[4-102],[113-147],[166-216]波段进行选择。数据对应的真实地物情况如图3所示,16种地物类型及数目由表1所示。

图3 Indian Pines数据Fig. 3 Indian Pines data
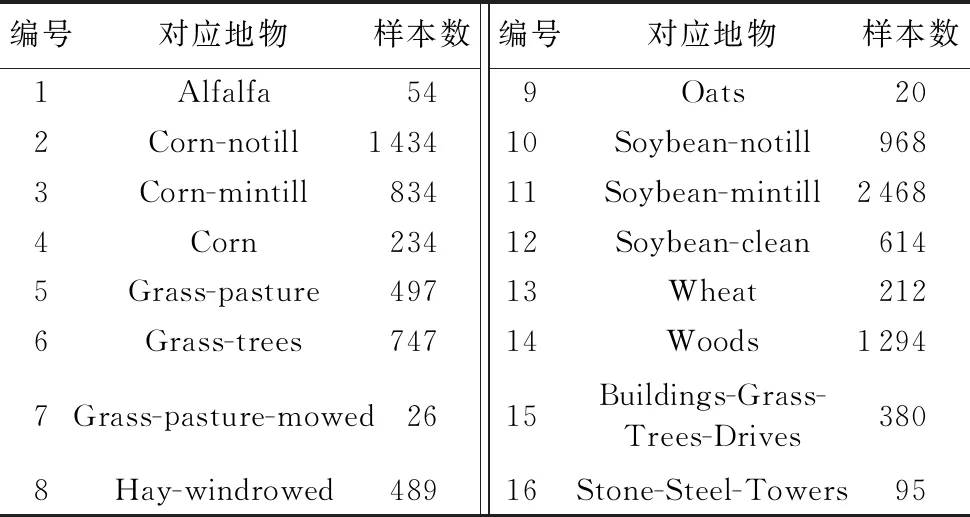
表1 印第安农林数据地物类别 Tab. 1 Culture feature categories of Indian agriculture and forestry data
3.2 其他比较算法
为了检测本文算法分类精度的优劣程度,本文算法FRS将与基于归一化互信息(Normalized Mutual Information, NMI)[7]、基于邻域粗糙集(Dependency Measure of NRS theory,DMNRS)[5]、最大信息量(Max Information,MI)[9]以及BCA[18]波段选择算法进行比较。
1)最大信息量高光谱波段选择算法。
高光谱图像波段的具体信息含量是很难衡量出来的,可以通过计算高光谱图像波段之间信息量的差,来间接计算高光谱波段的信息含量。使用相对熵可以衡量波段之间的信息量差。通过计算两个波段间最小的相对熵,迭代移除对整体高光谱图像信息含量影响最小的波段,最后留下的即为信息量大的波段子集,即波段选择的结果。相对熵的公式如下:
(8)
如果相对熵越小,说明两个波段之间的信息差异越小。
2)基于互信息高光谱波段选择算法。
通过计算波段图像与采集获得的地物真值信息,可以得到两者之间的统计相关性,因此可以用来评估每个波段对分类的相对效用,但是如果根据互信息大小直接进行选取则会产生波段之间的冗余。通过设置邻域宽度以及互补阈值的方式,避免将冗余的波段同时添加进波段选择子集。如果互补阈值过低,在将把目标波段选入的同时,会把邻接波段全部移除,这样可以减少冗余。
3)基于邻域粗糙集高光谱波段选择算法。
邻域粗糙集(Neighborhood Rough Set,NRS)是粗糙集理论的一种扩展,在特征选择中得到了广泛的应用。NRS具有处理连续型数据的优点。Liu等[5]提出的DMNRS算法邻域依赖关系来评估波段的重要性。当添加一个新的波段进入已选择子集时,能通过属性依赖度的变化情况衡量波段的重要性。变化越大,属性的重要性也就越大。
4)波段相关性分析波段选择算法。
BCA算法即基于波段相关性分析的高光谱波段选择算法。它首先根据皮尔逊系数计算高光谱波段图像间的相关性。算法随后计算每个波段与剩余未选择的全部波段的平均相关性以及已选择进波段子集的波段的平均相关性,根据两者关系每次挑选一个当前最佳的波段进入子集。
3.3 实验结果与分析
实验使用Java语言编写实现NMI[7]波段选择算法、MI[9]波段选择算法、DMNRS[5]波段选择算法、BCA[18]高光谱波段选择算法以及本文的FRS波段选择算法。通过上述算法获得选取后的波段子集。由于单一的分类器可能不能很好地衡量波段选择后的子集优劣,本文采用了J48、K最近邻(K-Nearest Neighbors,KNN)分类器进行分类精度比较。在WEKA默认的十折交叉的方式下,本文分别选择3~15个波段子集下的分类结果,进行实验分析。在KNN分类器中,本文设置近邻数为5。不同近邻数对分类结果有少量的影响,但是随着近邻数增加,计算复杂度也会增加,波段选择的有效性与近邻数无关。因而综合考虑,本文设置近邻数为5。
1)J48分类结果。
在J48分类器下,本文分析选择3~15个波段时候的分类精度变化情况。这里本文算法采用机器学习里最常用的高斯核,参数δ设置为0.32。实验结果如图4(a)所示。从图中发现,DMNRS算法在挑选5~10个波段时具有较高的分类精度,但是仍然比不上本文的FRS算法。BCA算法的分类精度略高于NMI算法和MI算法。MI算法在波段个数较少时分类精度比不上同期其他几个波段选择算法。本文提出的FRS算法分类精度优于其他波段选择算法。
2)KNN分类结果。
在KNN分类器下,本文分析选择3~15个波段时候的分类精度变化情况,同样采用高斯核,并将参数δ设置为0.32。实验结果如图4(b)所示。从图中可知本文提出的FRS算法一直都有较高的分类精度,且随着波段个数的增加,FRS算法的分类精度比其他算法有显著提高。DMNRS算法分类精度有较大波动,在9个波段后分类精度有所降低。MI算法仍然分类精度较低。
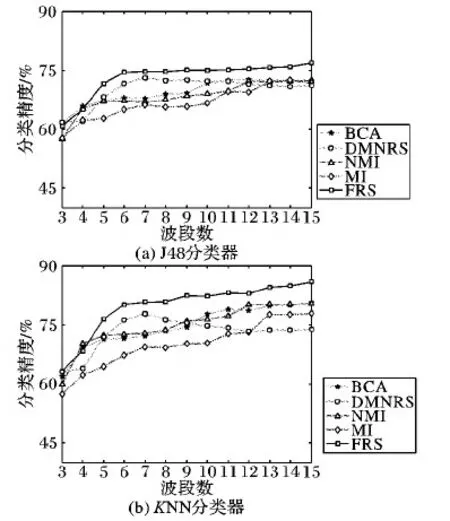
图4 不同波段选择方法分类精度对比Fig. 4 Comparison of classification accuracy of different band selection methods
3)不同核函数的结果。
本文测试了高斯核函数、指数核函数、二次有理核函数等3种不同的核函数,在参数设置为0.32时,选取的3~15个波段时分类精度变化情况。采用J48和KNN分类器时的实验结果分别如图5(a)、图5(b)所示。
从图5(a)、5(b)中可见高斯核函数在两个分类器下从挑选4个波段开始一直具有较高的分类精度。在J48分类器下,高斯核与二次有理核的分类精度大致趋同,比指数核普遍高一些。在KNN分类器下,二次有理核在挑选较多波段时分类精度不及另外两个核函数的分类精度。
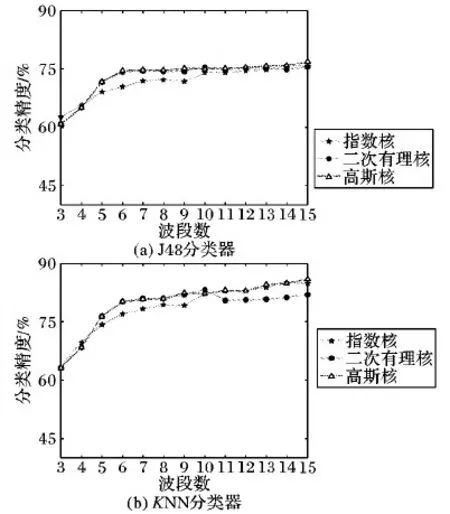
图5 不同核函数分类精度对比Fig. 5 Comparison of classification accuracy of different kernel functions
不同核函数下FRS算法在包含3~15个波段的情况下的总平均分类精度如表2所示。
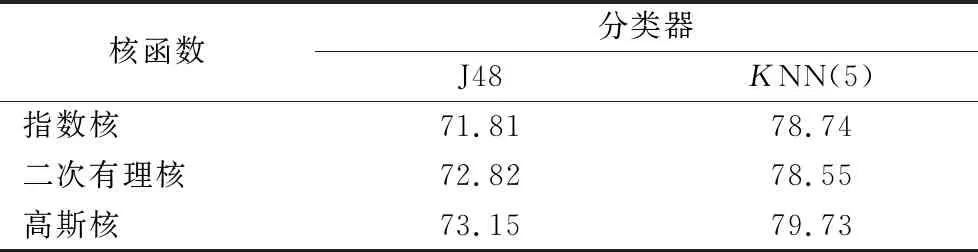
表2 不同核函数分类精度 单位:% Tab. 2 Classification accuracy of different kernel functions unit:%
从表2中可见高斯核的分类精度比指数核及二次有理核高。二次有理核在J48分类器下分类精度比指数核高,在KNN分类器下指数核比二次有理核分类精度高。
4)不同高斯核参数的影响。
由于不同的高斯核参数δ在计算波段之间相似性的时候会导致不同的结果,故可能选择出不同的波段子集。本文测试不同高斯核参数δ下选择的波段子集,并测试包含3~15个波段的情况下分类器J48和KNN的平均分类精度。这里设置高斯核参数为0.22,0.32,0.45,0.5,0.55,0.60。实验结果如表3所示。
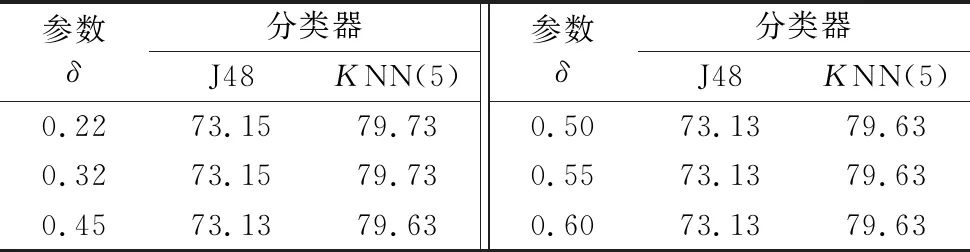
表3 Indian Pine平均分类精度 单位:% Tab. 3 Average classification accuracy of Indian Pine unit:%
从表3中可以发现,随着高斯核参数δ的变化,本文提出的FRS算法在J48分类器以及KNN分类器中一直具有较高的分类精度,且平均分类精度变化不大。
3.4 时间复杂度分析
由于本文算法要通过核模糊粗糙集的方式计算波段之间的相似性矩阵,故本文算法时间复杂度偏高。设图像像素数为n,波段个数为f,目标波段数为T,像素量化阶数x,类标个数y。本文算法首先计算每个波段图像的信息熵,时间复杂度为O(f·n)。随后计算波段图像间的相似度矩阵。由于需要计算每个像素与最近异类点的距离,求相似度矩阵的时间复杂度为O(f2·n2),搜索部分的时间复杂度为O(T·f2),最后本文提出算法的时间复杂度为O(f2·(n2+T))。DMNRS算法的时间复杂度为O(n2·f·T),BCA算法的时间复杂度为O((T+n)·f2),MI算法的时间复杂度为O((f+n-T)·f2),NMI算法的时间复杂度为O((T+x·y·n)·f)。虽然本文算法分类精度高,但是通过比较上述算法的时间复杂度,本文提出算法的时间复杂度偏高。
4 结语
本文根据模糊粗糙集理论,通过计算高光谱波段图像像素类标的下近似分布情况来得到波段图像间的相似性。随后在计算波段间相似性时引入信息熵的概念,该方法可以使得最后选出的波段子集中各波段间的冗余度小且各波段的信息含量大。实验结果表明,本文算法具有较好的效果。尽管本文工作产生了较好的效果,但是仍有一些可以改进的地方。比如目前大多数高光谱波段选择算法包括本文算法在内需要人工给定选择的波段个数,未来希望能自动计算出合适的波段数;同时,本文算法采用核模糊粗糙集的方式计算相似度,虽然效果较好,但是时间复杂度略高,如何快速计算是进一步的研究方向。

