双工位自锁电磁铁的设计与仿真

张 强,周 炜,乔桂玉,于长吉,邓 哲

(1.北京航天动力研究所,北京 100076;2.首都航天机械有限公司,北京 100076)

0 引言

随着航天技术的不断发展,20世纪80年代起,自锁电磁阀已广泛应用于国内外宇航型号中。这类阀门能在断电后自动保持断电前工作状态,从而满足系统对自动器组件的设计要求,特别是在长时间工作时,无源自保持功能避免了线圈的通电发热现象,提高了产品的可靠性和使用寿命。通常,电磁阀自锁形式分为三种:介质力自锁、机械自锁、磁性自锁[1-2]。前两种自锁形式结构复杂、外形尺寸偏大、可靠性低,而永磁自锁恰好弥补了这些不足,因此,国内外宇航型号中广泛采用了磁性自锁电磁阀。

磁性自锁电磁阀中的核心组件是自锁电磁铁,它的设计水平关乎着电磁阀的最终使用性能和可靠性,是整个电磁阀设计中的关键。本文以某型号实际产品为例,介绍了一种双工位自锁电磁铁的设计方法,并通过对电磁场的仿真分析与试验验证,阐述了双工位自锁电磁铁的性能特性。

1 自锁电磁铁工作原理

自锁电磁铁通常采用两个线圈分别控制开-关,在两线圈中间设置永磁体作为恒磁场源,形成极化磁场和控制磁场的双磁路结构,线圈通电,双磁场共同作用,吸合衔铁往复作动,以实现阀门的启闭。线圈断电后,利用永磁体对衔铁产生的极化吸力,使衔铁保持在断电前的位置不动,从而实现自锁功能[3]。自锁电磁铁结构图如图1所示。

1-壳体;2-线圈骨架;3-永磁体;4-衔铁;5-关线圈;6-开线圈;7-上导磁体;8-上挡铁;9-密封插座;δ1-衔铁在下位时的下气隙;δ2-衔铁在下位时的上气隙。图1 自锁电磁铁结构图Fig.1 Self locking electromagnet structure diagram

该结构中,衔铁处于下位为阀门打开状态,衔铁处于上位为阀门关闭状态。其中衔铁、上挡铁、上导磁体、壳体、永磁体形成上永磁闭合磁路,衔铁、线圈骨架、壳体、永磁体形成下永磁闭合磁路。磁通分布情况如图2所示。

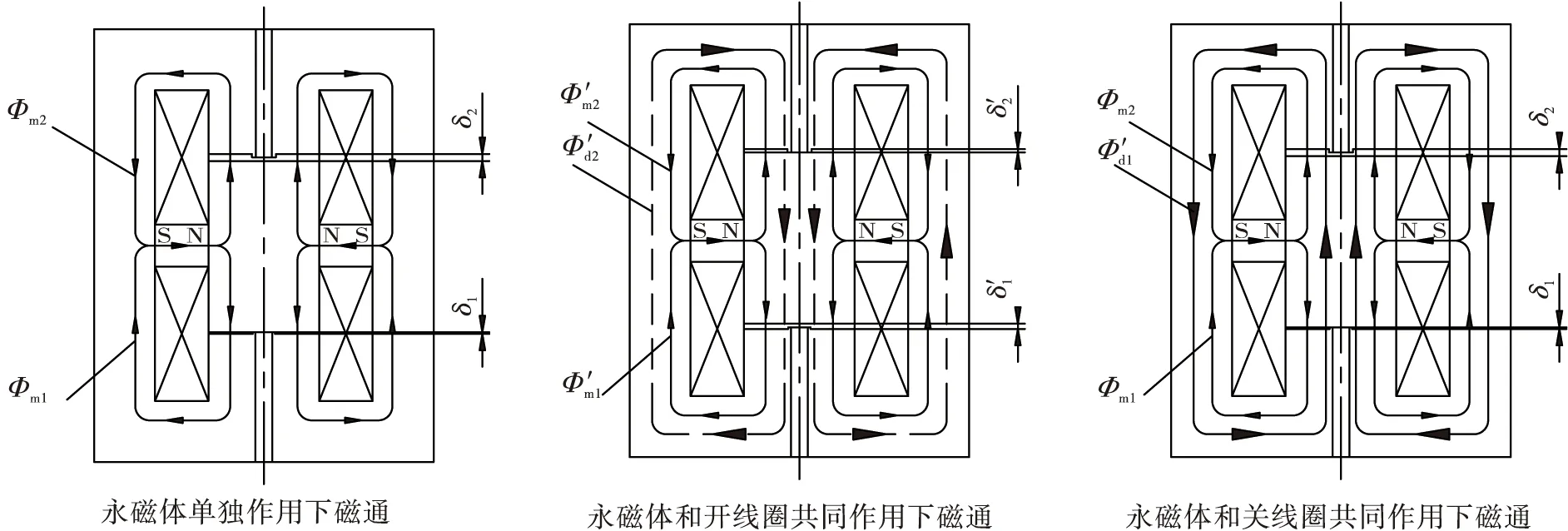
图2 磁性自锁电磁铁磁通分布示意图Fig.2 A schematic diagram of magnetic flux distribution of a magnetic self locking electromagnet

当衔铁处于下位时(δ1<δ2),根据磁路欧姆定律

W=ΦmRm

(1)

推导出

(2)

式中：W为磁势,A;Φm为磁通,Wb;Rm为磁阻, H。

当衔铁处于下位时永磁吸力向下,衔铁保持下位不动。同理,当衔铁处在上位时,永磁吸力向上,衔铁保持上位不动。因此电磁铁具备双工位自锁功能。

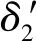
2 参数设计

我国新一代运载火箭XX-77发动机自锁阀即采用该种电磁铁结构,并通过多次发动机地面试车考核。以其为例,电磁铁参数设计从吸力入手,吸力设计值如下：衔铁在下位时永磁吸力Fdp=230 N,衔铁在上位时永磁吸力Fup=145 N,关线圈通电时(此时衔铁在下位)电磁永磁合力Fue=180 N,开线圈通电时(此时衔铁在上位)电磁永磁合力Fde=287 N。基于上述要求,电磁铁各参数取值计算如下：

衔铁在下位时的下气隙δ1取值0.2 mm,衔铁在下位时的上气隙δ2取值1 mm,衔铁行程h取值0.7 mm。永磁体单独作用时δ1处的磁感应强度Bm1取值1.2 T,永磁体单独作用时δ2处的磁感应强度Bm2可由式(2)计算。衔铁半径

(3)

永磁体工作点磁势

(4)

(5)

式中磁阻系数f取值1.4(无量纲)。

(6)

衔铁上吸所需关线圈磁势

(7)

式中：总气隙δh=δ1+δ2=1.2 mm;磁势降系数KΣ取值1.1(无量纲)。

由此关线圈电流与匝数可得,同理设计开线圈即可。

3 仿真模型

根据参数设计结果利用Ansoft Maxwell软件建立电磁铁模型(二维轴对称),采用自适应网格剖分工具对模型进行网格划分,如图3所示。

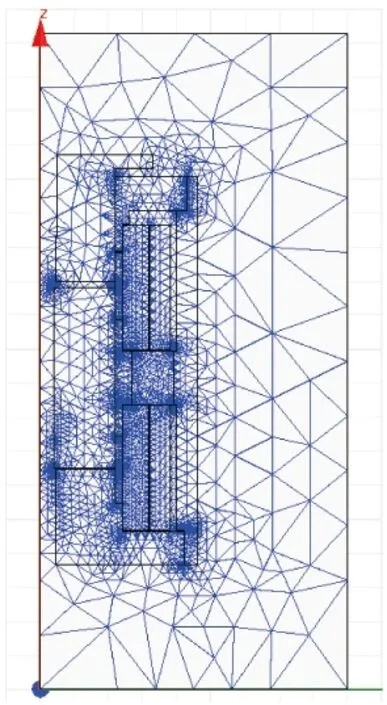
图3 网格模型Fig.3 Grid mode

材料属性：按表1所列电磁铁材料,分别对模型进行材料属性定义,其中衔铁、导磁体等材料选为电磁纯铁DT4E。

表1 材料模型属性Tab.1 Material model attributes

边界条件：自然边界条件规定两物体交界面磁场强度H的切向分量和磁通密度B的法向分量保持连续;诺依曼边界条件规定外表面只有切向磁场强度,法向磁场强度为零;气球边界条件将求解区域外边界设置为气球边界[6-7]。

4 计算结果分析

使用Ansoft软件进行二维静态电磁场仿真：励磁源设置为开线圈1 283 A、关线圈945 A(开关线圈安匝数设为满足产品设计要求所需的最小值)、永磁体导磁系数1.06,磁矫顽力-750 000 A/m,设置衔铁所受电磁吸力为求解量。

计算结果如下：永磁吸力Fup为159 N,永磁吸力Fdp=252 N,关线圈通电瞬间电磁永磁合力Fue=193 N,开线圈通电瞬间电磁永磁合力Fde=301 N。有限元仿真得到的计算结果与设计值误差均不超过10%,图4为仿真得到的以上4个状态磁场分布情况。磁力线越密,磁感应强度越大,4个状态下磁感应强度及分布情况展示了磁路工作原理。在线圈断电状态,永磁体作为唯一的励磁源为衔铁提供自锁力,磁力线能够很好地被约束在闭合磁路内,磁场较为稳定;在打开/关闭瞬间,开/关线圈通电,线圈形成的电磁场与永磁体形成的永磁场在衔铁所在位置一侧相互抵制,电磁场克服永磁场做功,驱动衔铁,因此整个磁场受到扰动而变得不稳定,部分磁力线逸出闭合磁路,产生一定漏磁[8-9]。

选取20台样本进行吸力试验,线圈通电27 V。测试结果：Fde=291～315.5 N;Fue=187.6～202.6 N。吸力仿真值、试验值对比情况如图5所示。图5中衔铁吸力试验值围绕仿真值窄幅波动,主要是由于永磁体/导磁材料个体磁性能差异、装配误差等原因造成,波动范围在7%以内,说明电磁铁参数设计较为合理,仿真计算较为准确。可见,在精度要求范围内,采用公式法设计电磁铁的途径简单可行,具有一定工程意义[10]。完成电磁铁设计后,有必要对电磁铁性能特性进行仿真研究,从而获得更多的设计指导信息。结合实际使用情况,主要考虑以下两方面仿真研究。

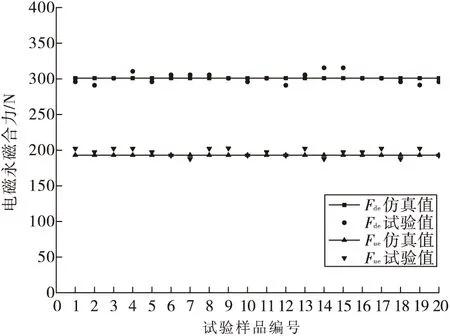
图5 电磁吸力对比Fig.5 Comparison of electromagnetic suction

4.1 衔铁工作气隙对永磁吸力的影响

调整下气隙δ1,范围0.1～1.1 mm,其他参数不变,对永磁吸力仿真计算。图6为永磁吸力FP随气隙δ1变化曲线。

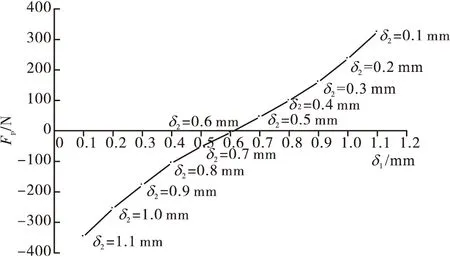
图6 不同气隙下的永磁吸力Fig.6 Permanent magnetic suction under different air gaps

图6中,δ1从0增至0.6 mm过程中,永磁吸力FP方向向下,数值从346 N减至0;当δ1为0.6 mm时,上下气隙一致,两方向永磁吸力相互抵消,值为0;δ1从0.6 mm增至1.2 mm过程中, 永磁吸力方向向上,数值从0增至324 N。下气隙调整过程中,永磁吸力曲线变化近似线性,基于此工程上可近似采用线性计算得到吸力[11-13]。图7为不同气隙下磁路磁力线分布图。磁力线越密,磁感应强度越大,δ1从0增至0.6 mm过程中,下磁路磁感应强度逐渐减小,上磁路逐渐增加,漏磁效应逐渐增强;δ1达到0.6 mm左右时,漏磁效应最强,部分磁力线不被约束在闭合磁路内,出现外逸;δ1从0.6 mm增至1.2 mm过程中,下磁路磁感应强度逐渐增加,上磁路逐渐减小,漏磁效应逐渐减弱。

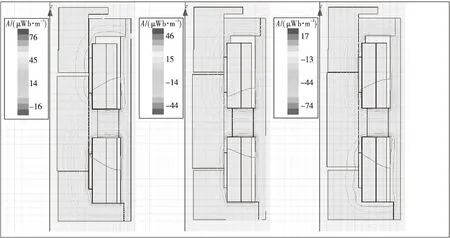
图7 不同气隙下的磁力线分布图Fig.7 Distribution diagram of magnetic line of force under different air gaps

4.2 励磁电压对动态响应特性的影响

电磁铁完成设计后,结构参数均已确定,而驱动电压作为唯一的外部励磁源直接影响着响应特性[14],考察励磁电压对响应特性的影响规律需进行瞬态电磁场仿真。本文仅考察电磁铁打开过程中线圈驱动电压对响应特性的影响,关闭过程规律相同,在静磁场分析模型基础上进行瞬态电磁场仿真。材料属性和边界条件设置同静态磁场分析。激励源由外部提供,脉冲电压各参数设置：V1=0,V2=27 V,Td=0,Tr=0.001 s,Tf=0.001 s,PW=0.1 s,脉冲周期0.15 s[15-18]。运动类型选择平动,初始位置为0,衔铁运动行程朝Z轴负方向0.7 mm,初始速度为0,衔铁质量0.1 kg,阻尼0.01 N·s/m。

经求解计算,得到电磁铁开线圈电流-时间曲线,如图8所示。

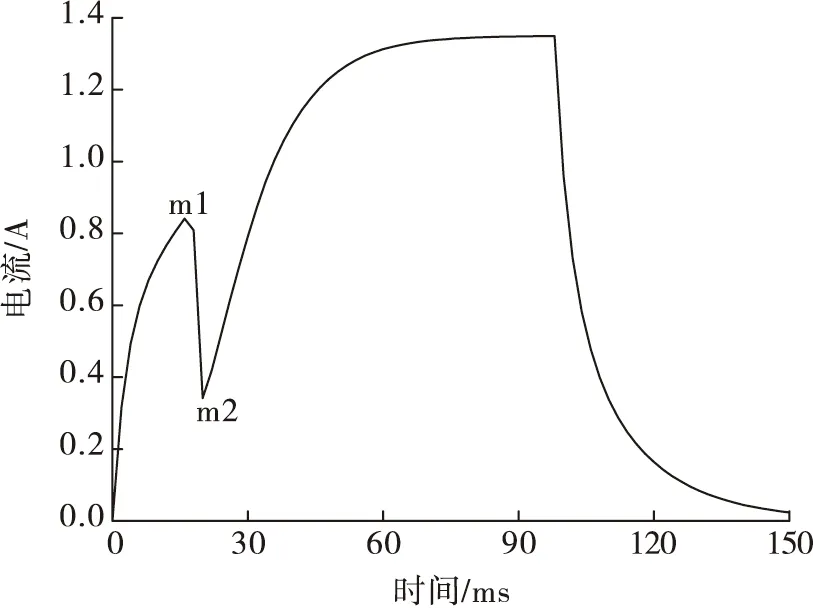
图8 励磁线圈电流曲线Fig.8 Excitation coil current curve

线圈通电时,电流曲线同典型螺管式电磁铁相似,电流值升高到触发电流(m1点)时,衔铁开始运动,此时对应的时间为触发时间,衔铁作动切割磁感线,线圈中产生反向电动势,电流有所减小,运动结束后电流逐步攀升直至稳态电流,衔铁运动结束时所对应的时间(m2点)即响应时间,稳态电流与触发电流的比值即为电流储备系数[19-22]。断电后,双工位自锁电磁铁电流曲线中不存在释放段,衔铁在电磁吸力撤去后依然能依靠永磁吸力保持在原位不动。将外部驱动电压设成不同值,分别求解可得到不同驱动电压下响应时间-电压曲线、触发电流/电流储备系数-电压曲线,如图9～图10所示。

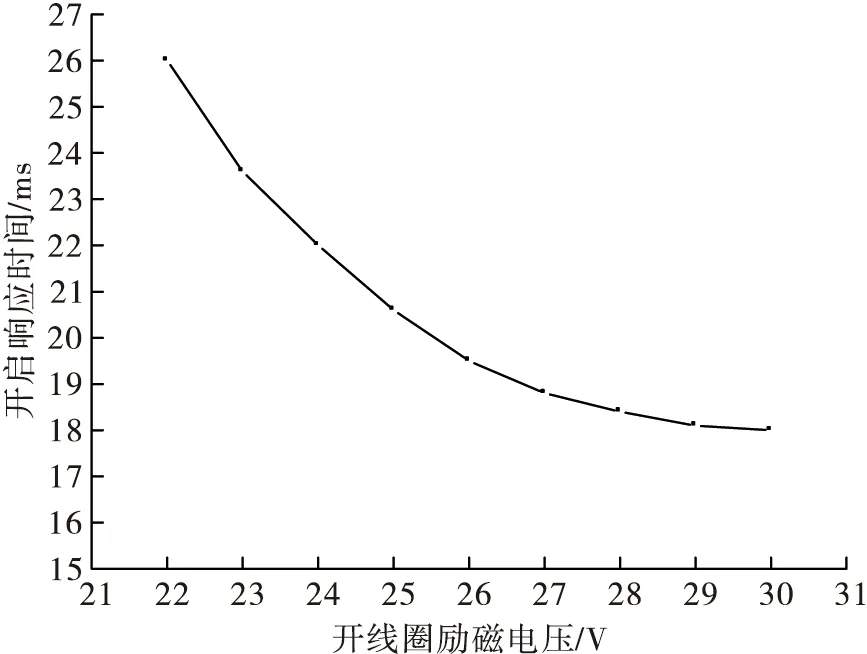
图9 不同驱动电压的响应时间曲线Fig.9 Response time curves of different driving voltages

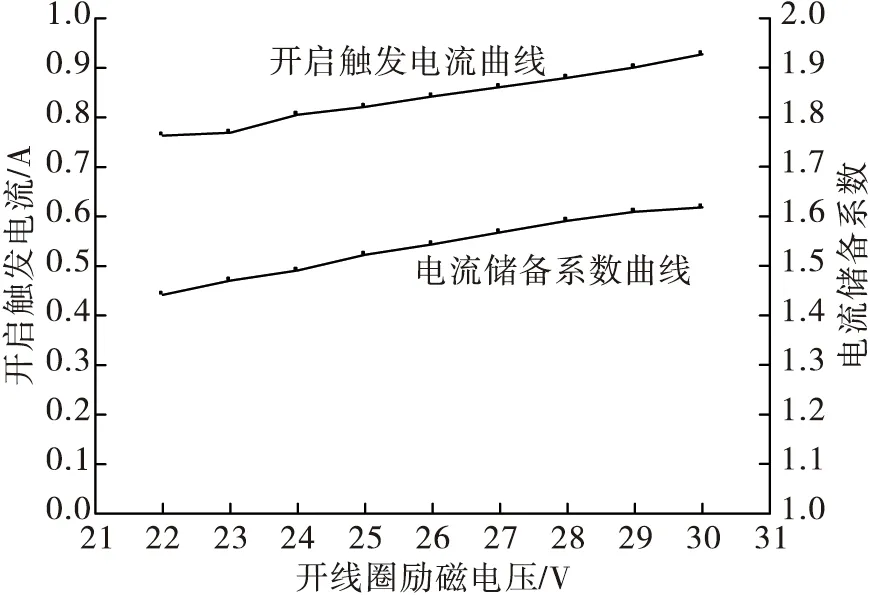
图10 不同驱动电压的触发电流/电流储备系数曲线Fig.10 Trigger current/current reserve coefficient curves with different driving voltages

图9中,随着驱动电压逐渐增大,电磁铁动作响应时间逐渐减少,但电压增大到一定程度后,响应时间变化很小,因此不能一味依靠增大驱动电压而减少响应时间。图10中,随着驱动电压逐渐增大,受线圈电感作用,其触发电流有一定增加,同时电流储备系数也逐渐增大,提高了电磁铁的作动裕度[23-24]。

5 结论

本文介绍了一种双工位自锁电磁铁的公式设计方法,通过仿真计算和试验测试考核了设计的准确性,表明该方法具有一定工程意义。后对电磁铁性能特性进行仿真研究得出：随着衔铁工作气隙增大,永磁吸力逐渐减小,当衔铁位于永磁体中间位置时,永磁吸力为0,越过中间位置后,永磁吸力反方向逐渐增大;随着驱动电压逐渐增大,电磁铁动作响应时间逐渐减少,但电压增大到一定程度后,响应时间变化很小;驱动电压增大,触发电流和电流储备系数增加,电磁铁的作动裕度有所提高。