多级涡轮气热耦合仿真性能及强度对比研究

张鹏飞,贾少锋,许开富,朱东华,任 众

(西安航天动力研究所,陕西 西安,710100)

0 引言

涡轮是发动机中热负荷和动力负荷最大的部件,工质温度高,工作环境恶劣。涡轮盘作为涡轮的关键件,整体结构较为复杂,直接承受燃烧室出口高温、高压和高速气流的冲击,所处的环境极端恶劣,由于热应力的存在,其局部区域有可能出现较大的应力、应变,从而导致各种失效故障的发生[1-6]。涡轮盘的温度及温度梯度分布,对涡轮盘的强度以及涡轮机的结构安全性有极为重要的影响。传统的气动仿真方法通常将固体壁面作绝热处理,通过CFD计算得到壁面温度条件进行涡轮盘强度校核;但真实状态下,因周围环境温度及接触部件间存在的温差,涡轮盘固体壁面存在强烈的热传递,涡轮盘的温度分布也相应发生变化[7-8],并进一步影响到涡轮盘的应力分布和结构强度安全特性。

本文采用气动仿真及气热耦合仿真,分别得到涡轮的气动性能和温度载荷,并进行涡轮盘的有限元强度仿真,对两者的结果进行了对比分析。

1 研究对象

以某型发动机涡轮为研究对象,该涡轮为全周进气冲击式涡轮,3级动力涡轮盘。流动及固体域示意如图1所示。

图1 涡轮流动及固体域示意图Fig.1 Schematic diagram of turbine flow and solid domain

气动仿真条件下,不考虑固体域,计算区域包括涡轮流道,级间密封和涡轮盘腔;气热耦合仿真中,除与气动仿真相同的流动域外,还包括固体域的涡轮盘及静叶盘。多级轴流涡轮工作过程中,涡轮盘承受的载荷主要有叶片及轮盘本身的质量离心力,涡轮盘各部位温度梯度导致的热应力,气动载荷(叶片传来的气体力和轮盘前、后端面上的气体压力),叶片及轮盘振动时产生的动载荷[3]。其中气动载荷、振动载荷对轮盘的静强度影响较小,载荷数据的影响也比较有限,所以本文进行强度计算时主要考虑材料为高温合金,其材料参数如表1所示。

表1 材料主要力学参数Tab.1 Main mechanical parameters of material

2 计算模型建立

2.1 计算网格

考虑到涡轮盘上均布的10个螺栓孔,以及互为质数的各级静动叶叶片数,在流动计算域的选取中,叶片通道按单通道选取,而盘腔流动域以及级间流动域则取1/10的扇形区域为计算域;固体温度场计算中旋转涡轮盘的计算域也取1/10的扇形区域,而静叶盘部分则根据相应的静叶片单通道角度进行选取[9-11],计算模型如图2所示。流动域和固体域的网格分别采用Ansys Workbench的Mesh模块中针对流动和结构的方式生成,并对流动边界层、叶顶间隙、泄漏间隙以及流固交界面处的网格进行加密。其中流体域网格数为1 373万,固体域网格数为416万。

图2 涡轮流动及固体域计算模型Fig.2 Calculation model of turbine flow and solid domain

2.2 边界载荷

利用商业软件CFX完成气动及气热耦合仿真,气动仿真中固体壁面按照绝热壁面处理,而在气热耦合中,流体域与固体域交界面给定流固交界面,其他非接触固体壁面则按绝热处理;气热耦合流动部分的边界条件与气动仿真相同。图3为气热耦合仿真的计算网格,去掉固体部分后剩下的即为气动仿真的网格。

图3 涡轮流动及固体域计算网格Fig.3 Calculating grid of turbine flow and solid domain

图4为涡轮盘有限元计算的网格。在利用Ansys Mechanical进行有限元仿真前,仿真得到的轮盘表面温度分布还需要插值到有限元网格上[12]。由于流场网格与有限元网格不一致,流固交界面上的温度数据需要通过插值算法传递到有限元网格节点上,作为有限元计算的温度载荷边界。同时,在有限元计算中,第Ⅰ级和第Ⅲ级固结在第Ⅱ级涡轮盘上,在第Ⅱ级涡轮盘内孔处给定周向约束,靠近第Ⅲ级一侧的端面上给定轴向约束,并给定轮盘转速[13]。

图4 涡轮盘有限元网格Fig.4 Finite element grid of turbine disk

3 计算结果

3.1 气动性能

表2给出了两种仿真方式得到的涡轮气动性能结果。图5给出了叶片通道中截面上的马赫数分布。两种方法得到的涡轮效率和流量的偏差非常小,仿真结果一致。但两者轴向力偏差略大,这主要是气热耦合仿真的壁面温度不同,使得近壁面处的传热特性发生变化,流动压力也随之改变。

图5 涡轮叶片通道中截面马赫数分布云图Fig.5 Mach number contour on the cross section in the turbine blade passage

表2 涡轮气动性能结果对比
Tab.2 Result comparison of turbine aerodynamic performance

参数气动仿真气热耦合偏差效率70.65%70.79%0.205%流量3.811kg/s3.812kg/s0.026%轴向力7635N7289N-4.747%

图6是仿真得到的涡轮盘表面的温度分布。气动仿真结果的温度范围为603～885 K,气热耦合仿真的结果为706～873 K;并且从温度云图也能看出两者温度分布存在较大差异,尤其是气动仿真结果在第Ⅲ级涡轮盘根部靠近第Ⅱ级涡轮盘侧出现了异常的高温区。

3.2 应力及位移

将图6的温度云图作为热边界条件,并考虑离心力的作用进行涡轮盘强度的有限元计算。气动和气热耦合仿真得到的涡轮盘位移如图7所示,气动结果的最大位移为1.39 mm,而气热耦合的结果为1.20 mm,两者都出现在叶顶位置,相差0.19 mm,相对偏差较大,对涡轮叶顶间隙的设计控制有较大影响[14-15]。

由两种仿真结果温度载荷计算得到的各级盘的等效应力见图8。由图8可知,离心力和温度载荷作用下各级盘的最大等效应力都出现在螺栓孔靠近盘心侧(Ⅱ级盘为腰形孔),气动仿真温度载荷下,Ⅰ，Ⅱ，Ⅲ级涡轮盘最大等效应力分别为835.45 MPa,717.11 MPa,655.55 MPa,而气热耦合温度载荷下的最大等效应力分别为721.12 MPa,673.7 MPa,547.75 MPa,最大等效应力偏差可达50～100 MPa。叶片根部区域的等效应力差值也达到了50～100 MPa,并且各级涡轮盘整个盘面上等效应力分布也存在着明显的差异。

图6 涡轮盘表面温度分布云图Fig.6 Temperature contour on the turbine disk surface

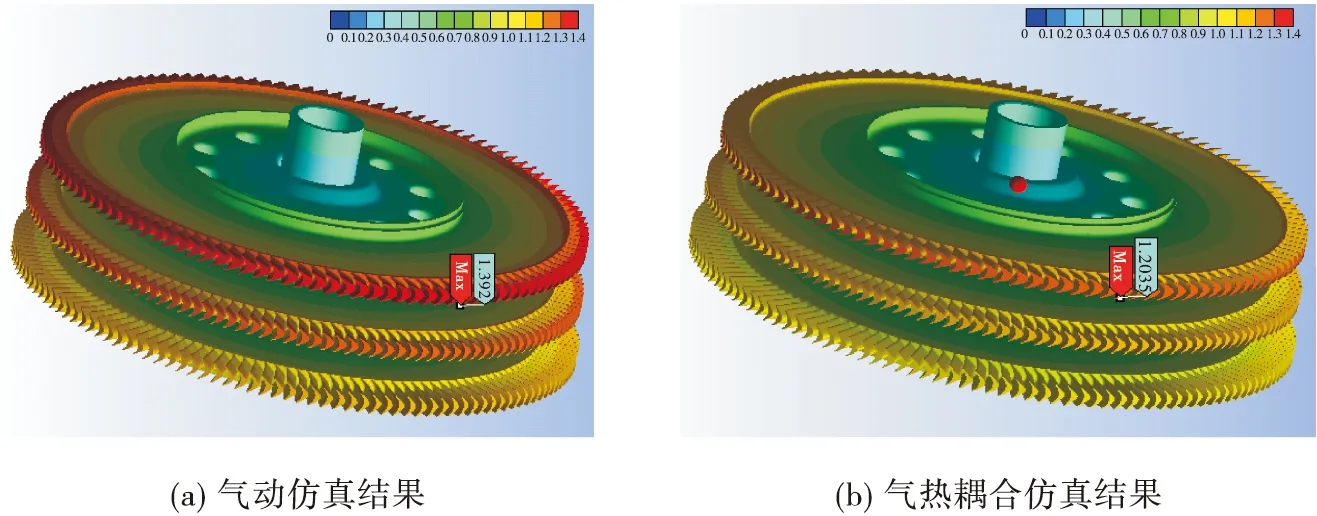
图7 涡轮盘位移变化图Fig.7 Displacement deformation of the turbine disk

图8 涡轮盘等效应力分布图Fig.8 Equivalent stress contour of the turbine disk

3.3 强度校核

利用有限元强度设计准则对上述结果的校核如表3～表5所示,由表可知,虽然两种仿真方法得到的最大等效应力存在较大的差异,但在相应温度条件下,材料的许用值仍有较大的安全裕量,并且全盘最大等效应力离最高温度下的许用值也有足够的安全裕量[16-17]，有限元结果满足要求[18-20]。

图9为使用塑性有限元强度仿真得到的整个涡轮盘的塑性变形量。可以看出离心力和气热耦合仿真温度载荷下的涡轮盘未发生塑性变形,处在安全范围内。而离心力和气动仿真温度载荷下的涡轮盘虽然根据业内普遍认可的准则,仍视为安全可靠,但可以看出与气热耦合下的结果还是存在差异的。

表3 Ⅰ级盘有限元校核结果Tab.3 Finite element check result of diskⅠ

表4 Ⅱ级盘有限元校核结果Tab.4 Finite element check results of disk Ⅱ

表5 Ⅲ级盘有限元校核结果Tab.5 Finite element check results of disk Ⅲ

图9 涡轮盘塑性变形Fig.9 Plastic deformation of turbine disk

4 结论

本文采用气动仿真及气热耦合对某三级轴流涡轮进行了仿真研究,得到了涡轮的气动性能和温度载荷,并进行涡轮盘的有限元强度仿真,对两者的结果进行了对比,得到以下结论：

1)气动仿真及气热耦合仿真得到的涡轮气动仿真性能高度一致,但由于壁面传热的作用,轴向力存在一定偏差。

2)以两种仿真结果的壁面温度作为载荷,并结合离心力进行有限元强度计算,得到的最大等效应力位置一致,但数值存在非常大的偏差;依据强度准则对有限元结果进行校核,虽然两者都满足强度准则要求,但有限元塑性计算结果依然有所差异。

3)综合以上分析可以看出,气热耦合结果充分考虑了固体传热的影响,相对气动仿真的结果更为可靠。