同质材料反射系统热特性研究

徐思华，彭小强，铁贵鹏，陈善勇，熊玉朋

（1.国防科技大学 装备综合保障技术重点实验室，湖南 长沙 410073；2.国防科技大学 智能科学学院机电工程研究所兼国防科技重点实验室，湖南 长沙 410073；3.超精密加工湖南省重点实验室，湖南 长沙 410073）

引言

随着光学仪器应用范围的不断扩展，温度适应性成为衡量其性能的重要指标。机械被动式、机械主动式以及光学被动式消热差方法常被用于光学系统无热化设计[1-2]，但稳定性、结构复杂性、准确性等问题限制了前两种方法的应用，光学被动式消热差方法在解决光学系统热问题上有着明显优势[3]。温度变化对光学系统的影响主要体现在光学元件几何参数、镜组间距和透镜折射率的变化上[4-5]，而反射系统的温度特性只表现为前两项。因反射系统设计参数较少，温度特性较为简单，采用同质材料（光学元件、支撑结构和镜筒等均为同一材料）的反射系统具有无热差特性[6]。国内外研究重点始终聚焦于透射系统的无热化[7-11]，对纯反射系统的温度特性鲜有报道，已有的研究也仅限于卡塞格林系统[12]，以及反射系统的材料选择与结构设计[13-15]，而在光学原理上缺乏相应完整的热性质模型。同时，热变形对于从本质理解反射系统温度特性具有十分重要的意义。因此，本文将热变形的特征及其具体计算方法与反射系统热差特性相结合，以期更好地表征后者的性质。

1 热变形的特征及计算方法

反射镜的温度效应表现为几何参数的改变，同时热变形也是光学系统热分析的基础，因此，有必要对热变形问题进行相应介绍。线性热膨胀系数：

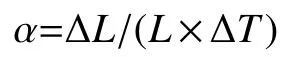
式中： ΔL为材料形变量；L为材料原始长度； ΔT为温度变化量，表征了特定材料在特定温度下由单位温度变化引起的单位长度量值的变化。

现考察任意形状物体的热变形情况。如图1所示，以曲线右端点(x1,y1)为对象，从“投影”视角可知，当该物体经历 ΔT的均匀温度变化后，有：

同理，从“分割”视角可知，有：

式中：dLxi=Lcosθ/n；dLyi=Lsinθ/n；n表示分割份数。该曲线上任意一点热变形后的坐标值均可由以上两种方法进行计算，且结果相同。若取坐标系2 为参考系，则同一点的新坐标变为(x1+b,y1+c)，热变形后的坐标变为(x1+x1αΔT+b+bαΔT,y1+y1αΔT+c+cαΔT)。可以看出，在不同坐标系下曲线上同一点受热变形的区别仅是坐标系不同带来的平移，曲线所处坐标系的不同与反射镜背部结构的不同是等价的。又因同质材料的反射镜在热变形中处于自由状态，所以反射镜光学面的热变形与反射镜背部结构无关，当反射镜的材料和初始面形确定，面形自身受热改变的情况就已确定。

图1 热变形计算示意图Fig.1 Schematic diagram of thermal deformationcalculation

由上述分析可知，对于反射镜光学面上任意一点(x,y) ，其热变形后的坐标为(x+xαΔT,y+yαΔT)，通过变量替换法将x=x′/(1+αΔT)，y=y′/(1+αΔT)代入原面形方程便可得到该反射镜热变形后的面形方程。

至此，我们对热变形进行了描述，给出了求解线性热膨胀理论且无约束条件下的热变形方法，并得到以下结论：

1）热变形的特征可用“投影”和“分割”两种视角理解，且“分割”就是微观的“投影”；

2）可对物体上任意一点热变形后的坐标值进行正交分解，分解结果只与该点与参考点在x和y向的投影或分割长度有关，所以反射镜光学面热变形只与其初始光学面形状、温差和材料热膨胀系数有关，而背部结构只是对该光学面产生平移效果；

3）反射镜面形由方程式表征后，热变形对应方程的改变可用变量替换法计算，且建立恰当的坐标系有利于简化计算。

2 反射系统的焦点温度特性

通过上述分析，以热变形的特征及其计算方法为基础，开展对反射系统温度特性的研究。焦点的偏移是光学系统热特性的重要体现，当焦平面与实际像面偏移量超过系统焦深时，成像质量便急剧恶化，因此，热离焦成为研究反射系统温度特性的关键问题。现以焦点为研究对象，从单反射镜的焦点温度特性出发，依次考察共轴反射系统、离轴反射系统的焦点温度特性，从而得出针对反射系统热特性的一般结论。

2.1 单反射镜的焦点温度特性

如图2 所示，由光学原理可知，该反射镜焦距f′=r/2 ，焦点为F′，假设其热膨胀系数为 α，当经历ΔT的均匀温度变化后，发生如图2 所示的热变形。以焦距f′等 于后焦距lF′，因此有：

图2 单反射镜焦点温度特性Fig.2 Focus temperature characteristics of single mirror

因反射镜的主平面始终与反射镜顶点重合，所

圆热变形后依然是圆（可通过变量替换法证明），其热变形只体现在半径值的线性改变上，于是从“几何”角度可知，反射镜热变形后的焦距即是其新半径值的一半，即：

又因r本身就是温度的函数，蕴含了焦点的温度特性信息，则从“解析”角度，将（3）式对温度T求（ α为反射镜热膨胀系数）得：导并代入

式（4）与式（5）便是单反射镜的焦点温度特性。可以发现“几何”和“解析”两种角度的计算结果一致，但后者更适合处理复杂反射系统。

若不考虑像差，实际像面应与焦平面重合，则对单反系统而言，有lBF=f′=lF′，lBF表示后截距。若结构件与反射镜热膨胀系数均为 α，则以反射镜光学面顶点为参考，像面的位移量ΔlBF=lBFαΔT，故热平衡后的后截距有如下关系：

式（6）表明因反射镜热变形引起的焦点位移量与原焦距对应镜筒的热膨胀量完全一致，即镜筒的热变形恰好对焦距的改变进行了补偿，所以焦平面在温度变化过程中将始终与实际像面重合，对于同质材料单反射系统而言不存在热差。

2.2 共轴反射系统的焦点温度特性

对于如图3 所示的共轴双反系统，给出其等效高斯光学系统图，如图4 所示。

图3 共轴双反系统Fig.3 Coaxial double-reflector system

图4 双反射系统等效高斯示意图Fig.4 Equivalent Gaussian diagram of dual reflective system

图4 中H表示主平面，S表示反射镜顶点间距。对于以上系统有：

式中： φ1、φ2分别表示反射镜1 和反射镜2 的光焦度； φ表示系统总光焦度。合并上述两式并写成焦距形式得：

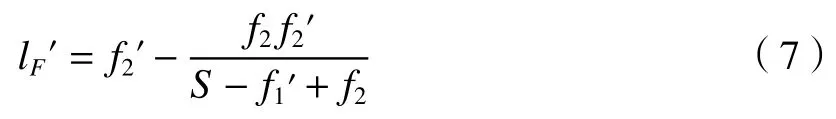
同理，将（7）式对温度T求导可得：

式中： αq表示结构件热膨胀系数； α表示两反射镜的热膨胀系数。故在经历 ΔT的均匀温度变化后，该系统后焦距的改变量为

后截距的改变量为

联立（8）式和（9）式可解得该系统由均匀温度变化引起的热离焦：

从（10）式可以看出，当α=αq时 ，TG=0，即同质材料共轴双反系统是无热差的。

因为共轴双反系统后截距lBF随温度的变化是线性的，即ΔlBF是线性的，而后焦距lF′随温度的变化与后截距保持一致，这说明可以用一个曲率半径为r0=2lBF=2lF′的反射镜（编号为0）代替图4 所示的双反系统，则它们在焦点的温度特性上是完全等价的，等效过程如图5 所示。

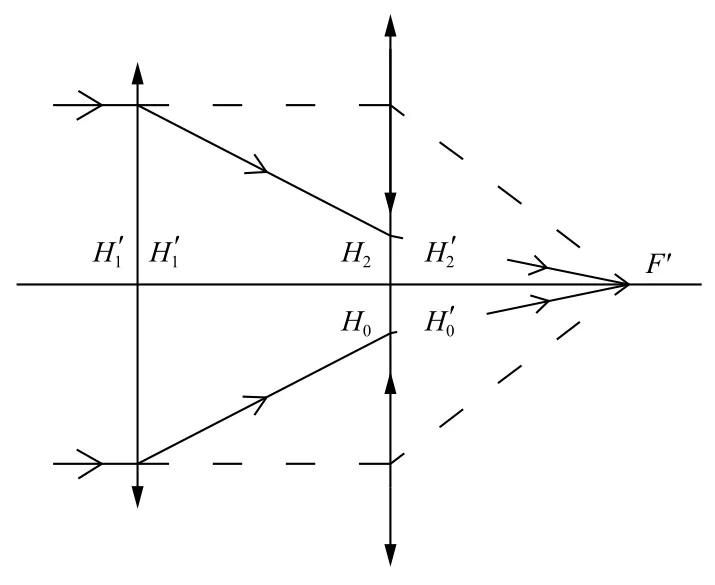
图5 单、双反射系统等效示意图Fig.5 Equivalent diagram of single and dual reflectivesystem

同理，对于如图6 所示的共轴三反系统，按照图5 所示过程将前2 个反射镜等效为一个反射镜（编号为0）后再与第3 个反射镜组合为等效的共轴双反系统，其后焦距lF′的计算方法与双反系统的完全一致，于是可以得到同样的无热差结论。采用类比的方法，用单反射镜代替多反射镜系统，再与新加入的反射镜组成针对后焦距而言的“共轴双反系统”，可得到同样的无热差结论，如果分组组合结果也相同。至此，我们便得到了同质材料共轴反射系统在均匀温度变化条件下无热差的结论。

图6 三、双反射系统等效示意图Fig.6 Equivalent diagram of three and dual reflective system

2.3 离轴反射系统的焦点温度特性

对于离轴的纯反射系统，依然从单反射镜开始分析。如图7 所示，半径为r的单反射镜与光轴夹角为θ。

图7 单反离轴系统焦点温度特性Fig.7 Focus temperature characteristics of single reflective off-axis system

定义反射镜几何焦点为FJ′，FJ′到反射镜顶点O的 距离称为几何焦距或几何后焦距，用符号lFJ′表示，则垂直于反射镜轴线并过反射镜几何焦点FJ′的平面定义为几何焦平面，用符号HJ′表示。根据光学原理可知，过反射镜顶点O的平行入射光线与几何焦平面HJ′的 交点即为像方焦点F′，故对图7 所示的单反系统有：

因 θ在热变形中不会改变，将后焦距即（11）式对温度求导，有：

后截距lBF=lF′，所以离轴的单反系统依然是无热差的。对于离轴多反系统，将其几何焦点的性质投影到光轴上来，并采用类似共轴多反系统的证明方法即可证明其具有无热差特性。

通过上述推导可以发现，均匀温度变化过程中反射系统焦点的位移或后焦距的改变只与反射系统材料的热膨胀系数有关，所以在无约束的理想状态下“同质材料”可理解为相同热膨胀系数的材料。但在实际光学系统中，常见的“同质材料”还是同种材料，最常用的便是铝合金。在温度变化不大的情况下，热膨胀系数相近的不同材料也近似满足“同质材料”条件，比如熔融石英和殷钢两种材料的组合。

3 验证实例与讨论

现以如图8 所示的红外离轴三反系统验证上述结论，该系统材料均为AL6061，故其热膨胀系数α=23×10-6/°C。该离轴三反系统在设计时并未进行过热优化。

图8 离轴三反系统原理图Fig.8 Schematic diagram of off-axis three-reflector system

由于反射镜在Zemax 软件中没有材料属性，故利用“跟随”命令和添加虚拟面的方法为反射镜赋予材料属性。在完成镜组空气间隔热膨胀系数设置后，建立-60 ℃、20 ℃、100 ℃ 3 个温度组态进行热分析，查看其在各个温度组态下的弥散斑大小和传递函数，结果如图9 和图10 所示。

图9 离轴三反系统弥散斑Fig.9 Dispersion spot of off-axis three-reflector system

从图9 可以看出系统弥散斑在各个视场和温度下基本都在艾里斑内（艾里斑半径9.754 μm），图10 表明各温度下系统的传递函数在70 lp/mm截止频率处均大于0.2，且在各个温度下传递函数基本保持一致。综上所述，该离轴三反系统拥有良好的温度适应性。

图10 离轴三反系统传递函数Fig.10 Transfer functions of off-axis three-reflector system

现分析该离轴三反系统后焦距随温度的变化情况，结果如图11 所示。其中-60℃温度条件下该系统后焦距为749.434 2 mm，而100 ℃时为752.197 2 mm，从图11 可以看出，其呈现明显的线性性质，图中直线的斜率同20 ℃时系统初始后焦距（750.815 7 mm）的比值与反射系统材料热膨胀系数一致，表明在设计温度20 ℃下，若像面与焦平面重合，则在整个温度区间焦平面将与像面始终保持重合，验证了同质材料反射系统无热差的结论。

图11 离轴三反系统后焦距变化Fig.11 Change in back focal length of off-axis threereflector system

因同质材料结构在均匀温度变化过程中不存在约束应力，可以得到同质材料反射系统在光学原理和机械结构上都具有无热化特性的结论。因此，同质材料反射系统在温度适应性上具有明显优势。同时，反射系统还具有无色差和能量衰减率低的特点，适用于远距离目标搜索[16]。

4 结论

本文探讨了同质材料反射系统热特性问题，表明用“投影”和“分割”两种视角可以很好地帮助光学设计人员理解无约束状态下镜面变形与反射镜背部结构无关的结论，变量替换法能够快速计算出反射镜在经历均匀温度变化后的面形。验证实例表明，当反射镜与镜筒等结构件采用同一材料时，机械结构可对反射系统因后焦距改变而产生的热离焦进行补偿，使得同质材料反射系统不存在热像差，保证了其在较大温差范围内具有良好的成像质量。