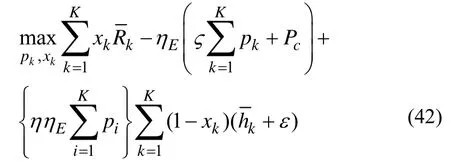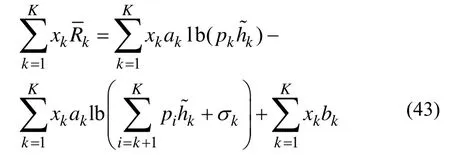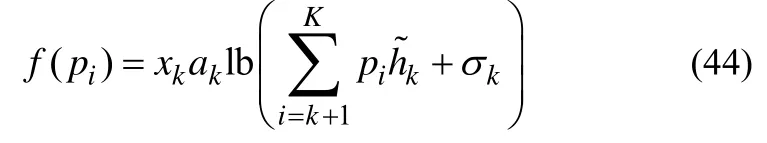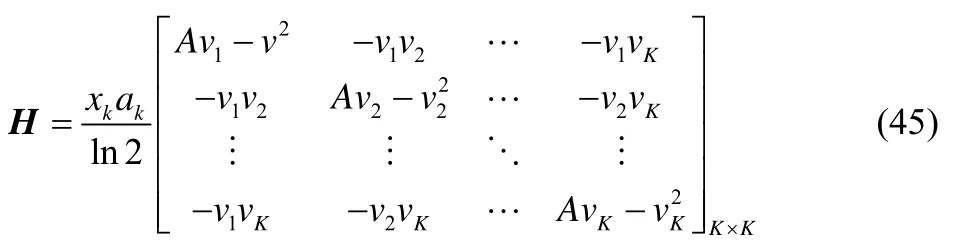基于非正交多址接入异构携能网络稳健能效资源分配算法

徐勇军，李国权，陈前斌，林金朝

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.山东大学山东省移动通信技术重点实验室，山东 济南 250100）

1 引言

随着移动通信技术的发展，各类无线终端和物联网设备对传输速率和频谱资源需求的剧增成为5G 移动通信系统需要考虑的关键问题之一[1]。在该背景下，巨大的能量消耗和日益短缺的频谱资源问题变得尤其严重。因此，5G 通信系统需要兼顾高传输速率和低能量消耗这两方面的问题。近年来，无线携能通信（SWIPT,simultaneous wireless information and power transfer）[2-3]被认为是解决无线通信设备节点能量短缺问题的有效技术。该技术的特点是充分利用射频信号具有同时携带数据信息和电磁能量的特点，在实现无线信息传输时，无线终端收集周围能量进行无线充电，从而延长通信设备在网运行寿命。另外，基于非正交多址接入（NOMA,non-orthogonal multiple access）[4]的移动通信系统允许多个用户终端共享相同的时间、频谱等资源，使系统容量进一步提升，受到人们的广泛关注。

因此，基于NOMA 的SWIPT 系统成为工业界和学术界的关注点。然而，由于差异化的用户需求和不同接入方式等因素的影响，导致目前蜂窝网络呈现出多层、异构的场景。基于低功率节点小蜂窝网络融合传统宏蜂窝构成的异构无线网络成为未来移动通信网络发展的趋势[5]。该网络可以有效提高网络传输效率和频谱利用率，同时减小覆盖盲区，因此研究基于NOMA 的异构携能通信网络相关技术具有非常重要的理论意义和应用前景。

资源分配是基于NOMA 的异构携能通信网络实现干扰抑制、提升能效的关键技术。通过调整基站发射功率和优化携能设备能量收集时间可以有效提高能量利用率、保护用户服务质量（QoS,quality of service）。文献[6]研究了基站配备多天线的NOMA 携能通信网络稳健资源分配问题，基于有界信道不确定性，研究了速率最大化的波束成形设计问题。考虑中断概率约束和统计信道状态信息，文献[7]研究了单天线NOMA 携能通信网络基于传输功率最小化的稳健资源分配问题，然而只考虑了2 个用户的通信场景。针对NOMA 认知携能通信网络，考虑用户最小速率约束和基站总发射功率约束，文献[8]研究了总吞吐量最大的功率分配和感知时间优化问题。针对能量接收机窃听信息接收机信号的NOMA 携能通信网络，考虑能量收集设备最小收集能量约束和信息用户最小速率约束，文献[9]研究了总安全容量最大的资源优化问题。然而上述工作都没有考虑能效问题。文献[10]研究了NOMA 携能通信网络能效优化问题，考虑基站最大发射功率约束和用户最小速率需求约束，利用Dinkelbach 方法进行问题转换与求解。基于中继辅助的全双工NOMA 携能通信网络，文献[11]研究了最优功率分流和波束成形问题。同时，其将提出的算法拓展到非完美信道状态信息的通信场景，然而不完美信道状态下的波束成形算法无法直接拓展到单天线NOMA 系统。考虑完美信道状态信息，文献[12]研究了NOMA 异构网络能效最大的子载波和功率分配算法。基于用户中断概率约束，文献[13]研究了异构携能通信网络能效最大的稳健资源分配问题，利用最小最大概率机方法提出了分布式资源分配算法。基于用户中断概率约束，文献[14]研究了异构NOMA 网络能效最大的资源分配问题，利用双边搜索方法获得功率分配策略。综上所述，对考虑参数摄动的异构携能通信网络在NOMA 协议下的稳健能效资源分配问题没有得到很好的研究。为了提高网络吞吐量、用户接入数、稳健性并降低能量消耗，对基于NOMA 异构携能通信网络稳健资源分配算法的研究具有非常重要的理论意义和现实价值。

本文主要的研究工作如下。

1)建立下行NOMA 两层异构携能通信网络资源分配模型。最大化多个微蜂窝用户能效，并满足最小能量收集约束、最小速率约束、最大跨层干扰功率约束、最大发射功率约束和有效时间切换约束。考虑目标函数和约束条件中的信道不确定性影响，建立基于椭圆球形有界信道不确定性下的稳健资源分配问题。该问题是一个非凸、非线性、多变量耦合的优化问题，很难直接获得解析解。

2)利用柯西不等式和最坏准则方法，将含参数摄动的约束条件和目标函数转换为确定性的形式。基于Dinkelbach 方法将目标函数转换为非分式规划问题。利用连续凸近似方法，将原问题转换为凸优化问题，并证明了目标函数的凸凹性。基于拉格朗日对偶原理和梯度更新算法获得解析解，同时给出了本文的算法步骤、计算复杂度分析和稳健灵敏度分析。

3)仿真结果表明，本文算法具有很好的时间切换和功率分配性能，并具有良好的能效性能。与传统非SWIPT 算法和非稳健算法对比，验证了本文算法的有效性。

2 系统模型

针对由一个宏蜂窝网络和一个微蜂窝网络组成的下行传输多用户两层异构无线网络，接收机含能量收集电路与串行干扰消除功能，如图1 所示。每个子信道可以被多个微蜂窝用户（FU,femtocell user）使用，信道最差的终端用户优先被解码，并将解码信息广播给其他信道好的用户，从而实现干扰消除，减小共道干扰。每个终端含有信息解码和能量收集电路，通过时间切换方法来区分信息与能量信号。假设所有用户和基站配备单根天线，网络中有M个宏蜂窝用户（MU,macrocell user）和K个微蜂窝用户，分别用集合∀m∈{1,2,…,M}和∀i,k∈{1,2,…,K}表示。由于下行传输中宏基站发射功率远大于微蜂窝，因此为了避免对微蜂窝用户过强的共道干扰和接收机端的串行干扰消除复杂度，假设宏用户在进行NOMA 传输时每个子信道只允许2 个用户同时工作[15-16]。假设在单位时隙里，xk和1-xk分别表示微蜂窝用户k用于信息解码和能量收集的时间。对于任意用户，假设信道增益满足h1≤h2≤ …≤hi≤hk≤ …≤hK，并考虑单位带宽子信道。系统参数如表1 所示。

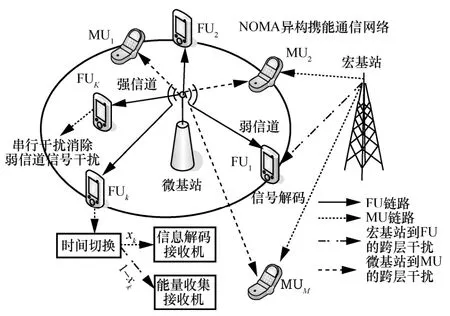
图1 下行NOMA 异构携能通信网络

由于当前用户k可以检测到比它信道弱的用户信号并消除该干扰信息，其数据速率可以描述为

表1 系统参数

为了保证每个宏用户的通信质量，微蜂窝的发射功率需满足

由于基站发射功率不可能是无穷大，因此微蜂窝用户总的发射功率满足

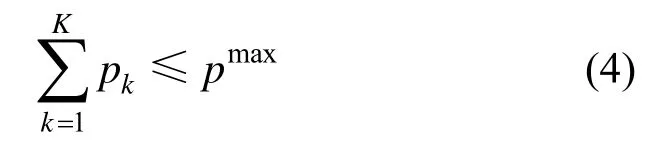
考虑SWIPT 的影响，每个用户接收机端收集到的有效能量为

为了延长网络设备运行寿命，考虑到每个能量接收机存在一个最小收集门限，能量收集同时应该满足

考虑电路功率消耗的影响，微蜂窝网络总的功率消耗为

由于能量收集能对功率消耗进行补偿，因此微蜂窝网络真实的功率消耗为

因此，系统总的能效可以定义为

假设基站可以获得完美的信道状态信息，可以建立如下能效最大的资源分配模型

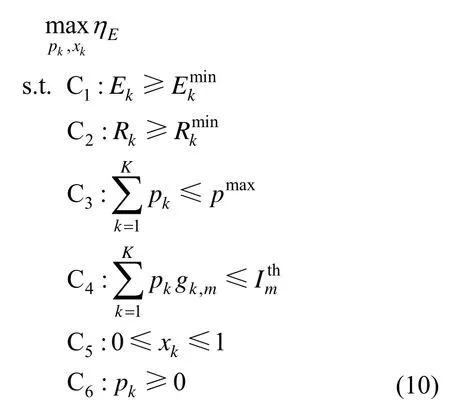
显然，由于目标函数和约束条件 C2的影响，式(10)优化问题是一个多变量耦合、非凸优化问题，不容易直接获得功率分配和时间切换系数的解析解。约束条件 C1和 C2决定有效发射功率的下界，约束条件 C3和 C4决定有效发射功率的上界。另一方面，由于该问题假设真实的信道增益hk和gk,m与信道增益估计值相等，即和，该优化问题为非稳健优化问题（也可以称为名义优化问题）[17]。然而在实际的NOMA 异构携能通信网络中，因为有串行干扰消除残留误差、能量收集非线性特性以及无线信道的随机性、时延等因素的存在，导致获得完美的信道状态信息这一假设过于理想，不满足实际物理通信场景。因此，对于克服信道不确定性（即Δhk≠ 0,Δgk,m≠ 0）、提高网络稳健性的问题研究显得尤其重要。

3 算法设计

3.1 稳健问题描述与转换

根据稳健优化理论可知[18]，对不确定性参数的建模有基于误差统计模型的贝叶斯近似方法和基于有界不确定性参数的最坏准则方法。由于下垫式频谱共享机制需要保证宏用户的性能不受其他用户的影响，即不允许用户中断事件的发生，因此基于有界不确定性的最坏准则方法更适合本文所讨论的网络场景，可以满足所有估计误差存在的情况，保护各类用户的通信质量，确保无中断发生。从式(10)优化问题的讨论可知，不确定的信道增益参数由其估计值和加性估计误差组成。因此，信道不确定性可以描述为

其中，Rg和Rh分别表示微蜂窝基站与宏用户之间信道不确定性集合和微蜂窝用户之间的信道不确定性集合；εm≥ 0表示微蜂窝网络对第m个宏用户接收机所有信道链路不确定性平方和的上界，当εm=0时，估计信道增益等于实际信道增益，此时没有信道估计误差，该情况等价于式(10)，εm越大，意味着对于宏用户m接收机来讲，信道摄动和随机性大，从而需要对该类用户进行保护；gm和Δgm分别为估计的信道增益和相应的估计误差向量，即gm=[g1,m,…,gK,m]T和Δgm=[Δg1,m,…,ΔgK,m]T；δk≥ 0表示任意微蜂窝链路信道增益不确定性的上界；ε≥0 表示所有微蜂窝用户链路信道不确定性和的上界，且满足。

根据上述不确定性描述，式(10)可以描述为

根据最坏情况准则，在任意信道不确定性下都需要满足以上约束。因此，目标函数可以转换为在信道估计误差下使最小的能效最大化，因此式(13)问题可以转换为

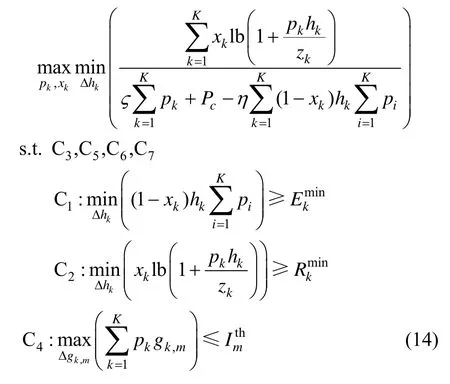
式(14)问题可以等价为

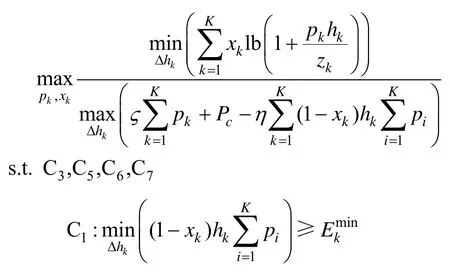
式(15)显然是一个含参数摄动的无穷维、非凸优化问题。因此，需要将上述含信道不确定性的优化问题转换为确定性优化问题，再将该确定性优化问题转换为凸优化求解。

根据式(11)和式(12)的不确定性描述，可以将约束条件 C1和 C2等价转换为

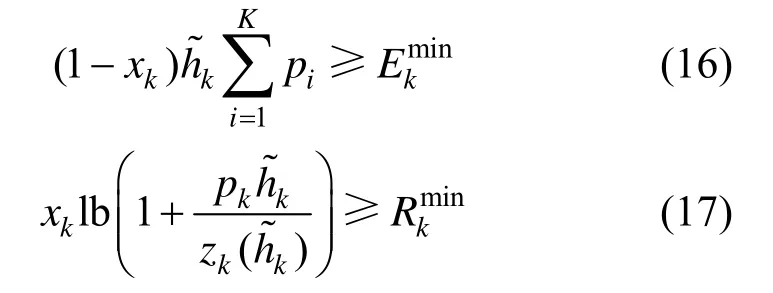
虽然式(18)是一个确定性的凸约束条件，但是由于功率的平方不易得到解析解，因此根据，含不确定性参数的跨层干扰约束可以缩放为

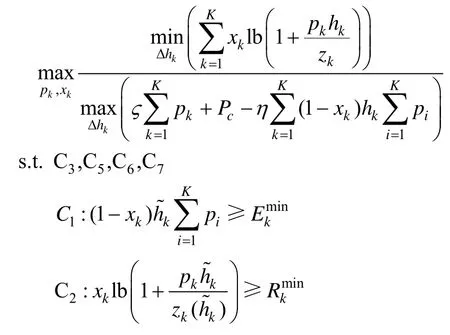
目标函数依然是一个含不确定性参数且不易处理的问题。由于Dinkelbach 方法[19]被普遍应用于处理非线性分式优化问题，因此本文应用该方法处理能效目标函数。基于Dinkelbach 方法，借助辅助变量ηE，目标函数可以转换为

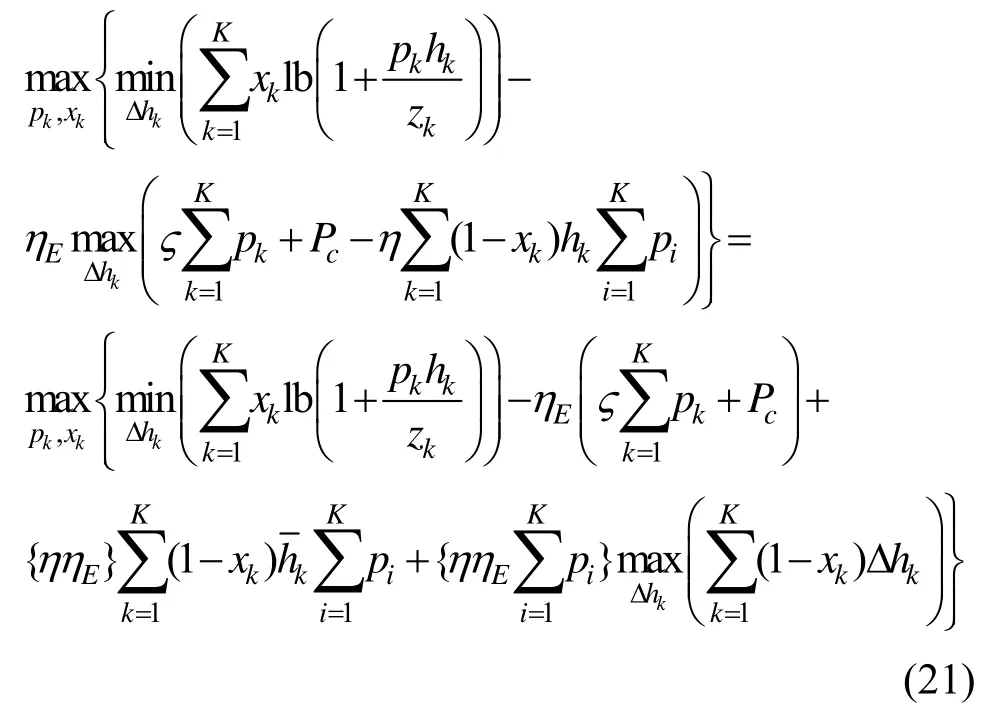
根据式(16)～式(18)的方法，目标函数可以转换为

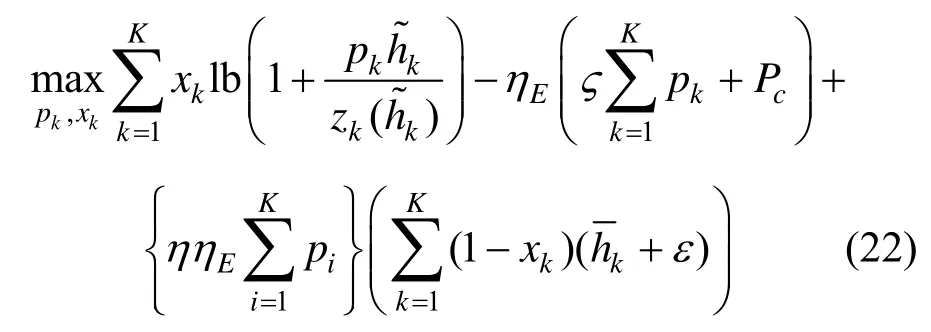
因此，式(20)问题可以转换为

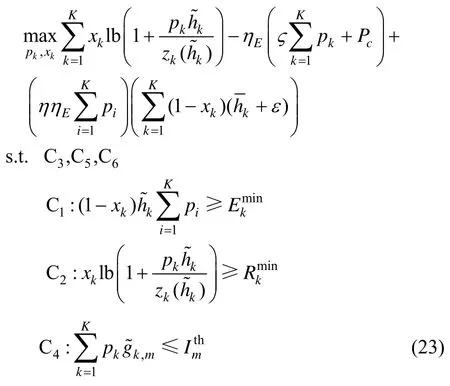
由于速率函数的影响，式(23)问题依然是个非凸问题。采用连续凸近似方法[20]，基于信干噪比（SINR,signal to interference plus noise ratio）的速率函数可以近似为。其中的初始值为系统参数初始化所对应的初始值。因此式(23)问题变为

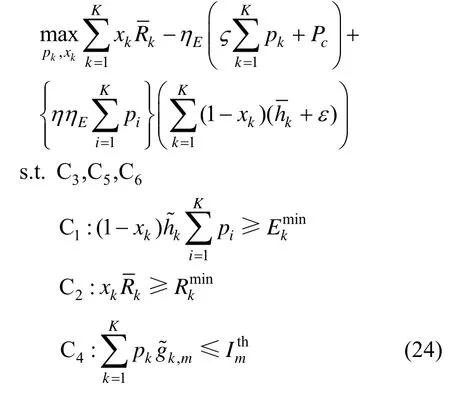
由于约束条件都变为线性约束，因此它们都是凸约束条件。然而目标函数中对于变量{pk},∀k的凸凹性需要通过多变量海森矩阵的正定性来判断。

定理1对于确定的参数η,ηE,ε,δk，目标函数是关于变量pk,∀k的严格凹函数。

证明详见附录1。

3.2 稳健功率分配算法设计

根据式(24)问题的描述，可以构建如下多变量拉格朗日函数。

其中，λk≥0,βk≥0,αm≥0,χ≥ 0和ϖk≥ 0是拉格朗日乘子。式(25)可以重新描述为

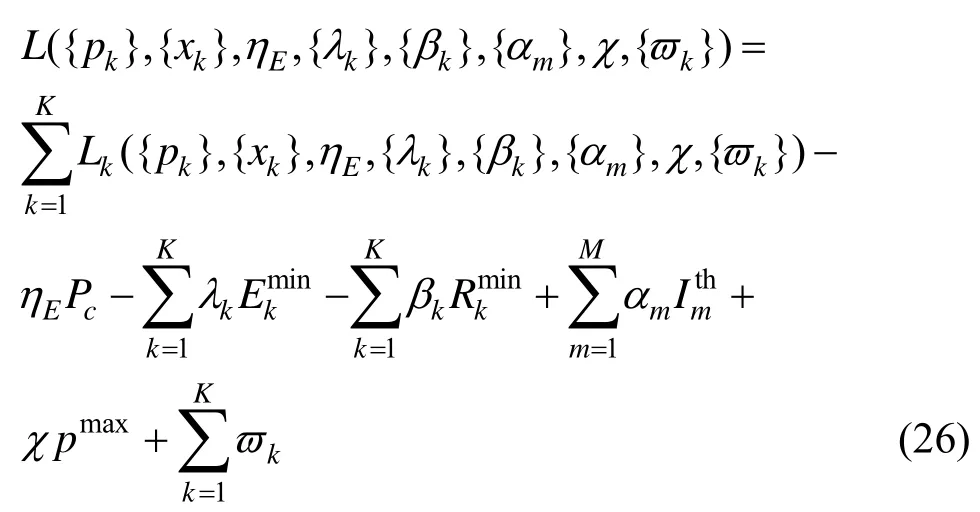
其中，有

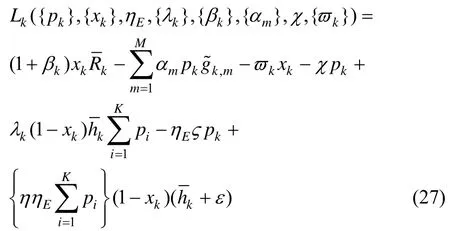
对于给定的能效ηE，式(24)问题的对偶问题为

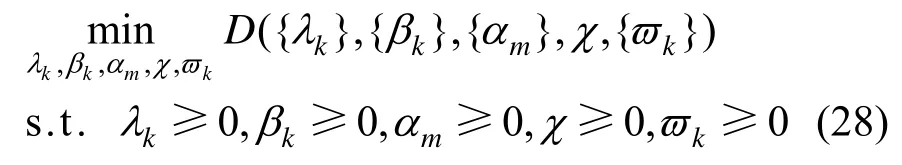
其中，对偶函数为

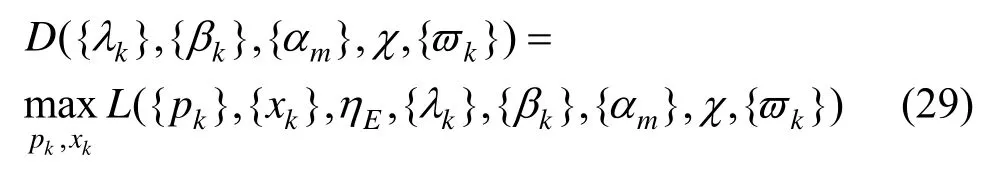
从式(28)和式(29)可以看出，对偶分解将原问题转换为两层优化问题。内层循环求解最优功率{pk}和时间切换系数{xk}，外层迭代更新求解拉格朗日乘子。根据KKT 条件[3]，最优功率可以得到

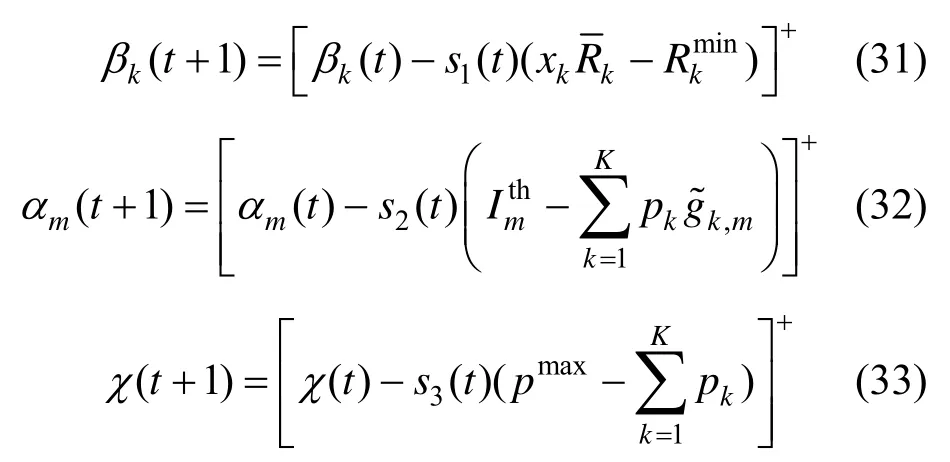
其中，[x]+=max{0,x}，t为迭代次数，s1(t)、s2(t)和s3(t)为正的迭代步长。基于确定的能效和时间因子，功率分配算法如算法1 所示。根据所求的最优功率，最优能效更新算法如算法2 所示。

算法1基于对偶理论的迭代功率分配算法

算法2基于迭代的最优能效更新算法

3.3 稳健时间切换控制算法设计

显然式(34)问题是含有线性目标函数和凸约束条件的线性规划问题，可以根据函数单调性求解。根据式(34)问题的形式，最优的时间切换系数为

因此，基于上述结论，最终的基于迭代的稳健能效最优联合功率分配和时间切换算法如算法3 所示。

算法3基于迭代的稳健能效最优联合功率分配和时间切换算法

4 性能分析

4.1 计算复杂度分析

由于在NOMA 系统中，用户接收机端的干扰消除与用户设备数量相关，因此根据现有文献[21]可知其复杂度为O(K2.376)。由于Dinkelbach 方法的计算复杂度与迭代精度和用户数相关[19]，即。根据梯度更新算法式(30)～式(33)，可以得到功率收敛的计算复杂度为O(MK)。假设π1,π2决定的最大迭代次数为T，则总的计算复杂度为。

4.2 稳健性分析

为了分析不确定参数对系统性能的确定性影响，描述稳健算法和最优算法（即非稳健算法）之间的能效差异，本节将分析稳健性代价问题，即非稳健算法和稳健算法效用函数之间的关系。根据稳健灵敏度分析可知[22]，在微小摄动因子影响下，可以假设2 种算法具有相同的最优功率和拉格朗日乘子。根据式(25)的拉格朗日函数，可以得到

又因为lb(a+b)≥lba+lbb，则有

根据泰勒展开可以得到

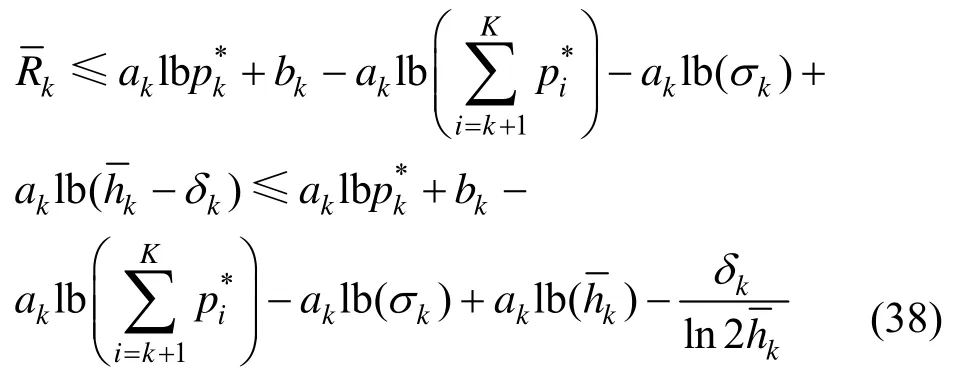
因此，稳健优化问题与非稳健优化问题的间隙为

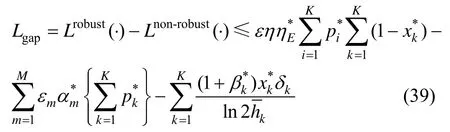
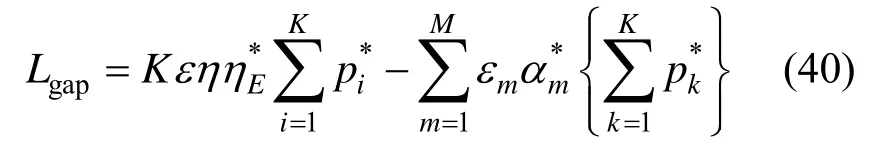
当C4成立时，宏用户得到很好的保护，则，有

因此，Lrobust≥Lnon-robust，本文稳健资源分配算法的能效大于非稳健资源分配算法。

5 仿真分析

为了验证本文算法的有效性，将其与非SWIPT的最优资源分配算法[23]以及基于SWIPT 的最优资源分配算法[24]对比。假设系统存在2 个微蜂窝和一个宏蜂窝用户，宏蜂窝和微蜂窝的小区半径分别为500 m 和20 m，宏蜂窝和微蜂窝基站间的最小距离为50 m，宏用户信道衰落模型为128.1+37.6logddB，微蜂窝用户的信道衰落模型为122+38logddB。其他仿真参数为功率放大器效率因子ς=0.38，能量收集效率系数η=0.1，接收机背景噪声为σk=10-8mW，微蜂窝基站最大发射功率门限为pmax=1 mW，电路总功率效率Pc=0.02 mW，最小传输速率需求门限为2 kbit/s，最小收集能量需求为0.02 mW。

图2 给出了不同干扰功率门限下微蜂窝用户总的能效性能。从图2 中可以看出，随着宏用户可以忍受的干扰门限值增加，微蜂窝用户总的能效下降。因为大的干扰门限可以使微蜂窝用户进一步增大发射功率来提高用户的QoS，但是由于能效函数是关于功率的递减函数，因此随着功率的增大能效值减小。而从信道不确定性上界对微蜂窝网络能效性能影响来看，随着不确定性参数的增加，系统能效随之增加。因为大的不确定性参数，意味着信道估计值偏离其真实程度较大，使微蜂窝网络降低发射功率，防止给宏用户带来过多的有害干扰，从而使能效增大。

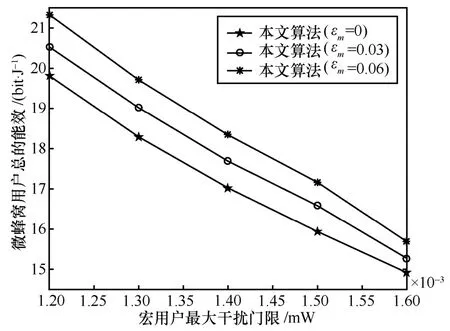
图2 微蜂窝网络能效与宏用户干扰门限之间的关系

图3 给出了不同用户在变化的最小速率门限下的最优时间切换系数，假设用户1 的信道好于用户2 的信道。从图3 中可以看出，随着用户速率需求的增加，最优用户时间切换系数随之增大。因为最小速率门限提升，会使每个用户需要达到更高的QoS 需求，因此通过分配更多的时间进行信息传输，减小能量收集时间可以有效地提高用户的传输速率来实现期望性能。由于用户2 的信道条件比用户1 的信道条件差，因此用户2 的时间切换系数大于用户1 的时间切换系数，从而补偿信道差异带来的性能损失。进一步可以发现，随着不确定参数增加，用户的最优时间切换系数增大。因为不确定性增加会减小有效发射功率的调节范围，从而通过提高有效的时间切换系数来使能效进一步提升。

图3 微蜂窝用户实际切换系数与最小速率门限之间的关系

图4 给出了微蜂窝用户总的能效与最小速率门限在不同干扰信道不确定性下的关系。假设宏用户最大干扰门限为0.002 mW，最小能量收集门限为0.02 mW。仿真结果表明，随着最小速率门限的增大，微蜂窝用户总的能效增大。因为速率门限的提高会使最小发射功率增加来满足每个用户的服务质量，使用户速率得到较大程度的提升，最终提高了系统总的能效。另一方面，本文算法在较小参数不确定性下的能效低于较大参数不确定性的能效。因为随着干扰功率约束中信道不确定性的增加，会降低最大可行的发射功率，从而使总的功率消耗降低。

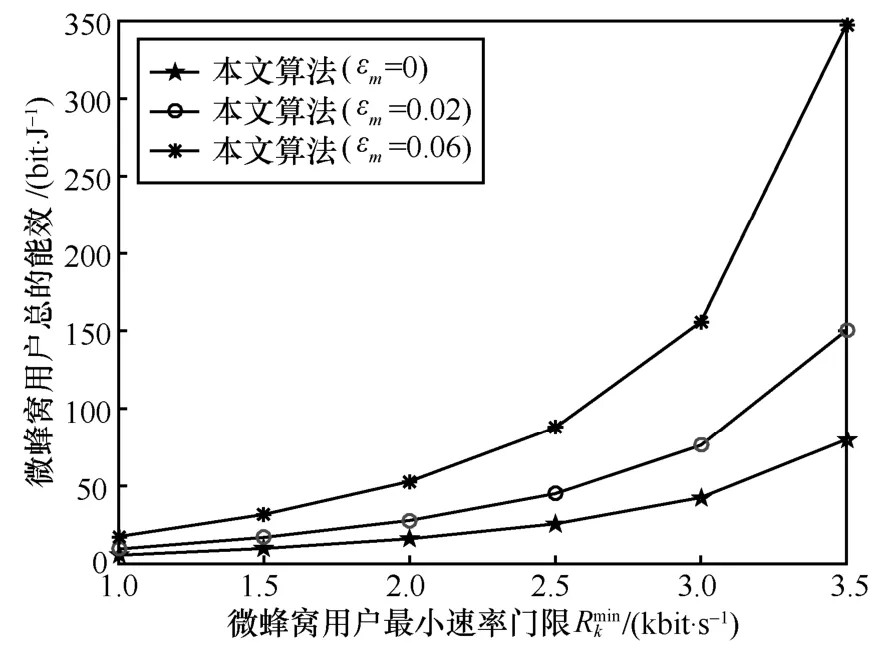
图4 微蜂窝网络能效与用户最小速率门限的关系

图5 给出了微蜂窝用户总的能效随最小能量收集门限的变化关系。假设宏用户最大干扰门限为0.001 mW。结果表明，随着最小能量收集门限的增加，微蜂窝用户总的能效降低。说明系统要求收集更多的能量来实现数据传输，从而降低了数据传输时间，减小了总的数据速率导致能效降低。同时，随着速率中信道不确定性参数增大，系统总的能效逐渐减小。在确定的最优功率条件下，该不确定性参数是关于目标函数的递减函数。也就是说，随着速率约束不确定性增大，为了防止微蜂窝用户出现中断，通过提高发射功率来满足每个用户的QoS 需求，使功率消耗增大，总的能效降低。

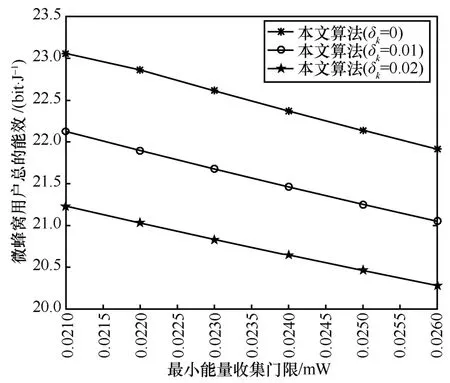
图5 微蜂窝用户能效与最小能量收集门限的关系

图6 给出了平均切换时间与最小能量收集门限的关系。随着最小能量收集门限增大，用户的时间切换系数随之减小。从式(35)可以看出，该能量门限与用户的时间切换系数成反比关系。从物理意义上来看，最小能量收集门限的提升，说明系统关注于更多的收集无线信号能量用于上行传输或存储起来，从而降低了用户的有效信息传输时间，且随着用户速率中信道不确定性因子的增加，微蜂窝所有用户的平均时间切换系数延长。

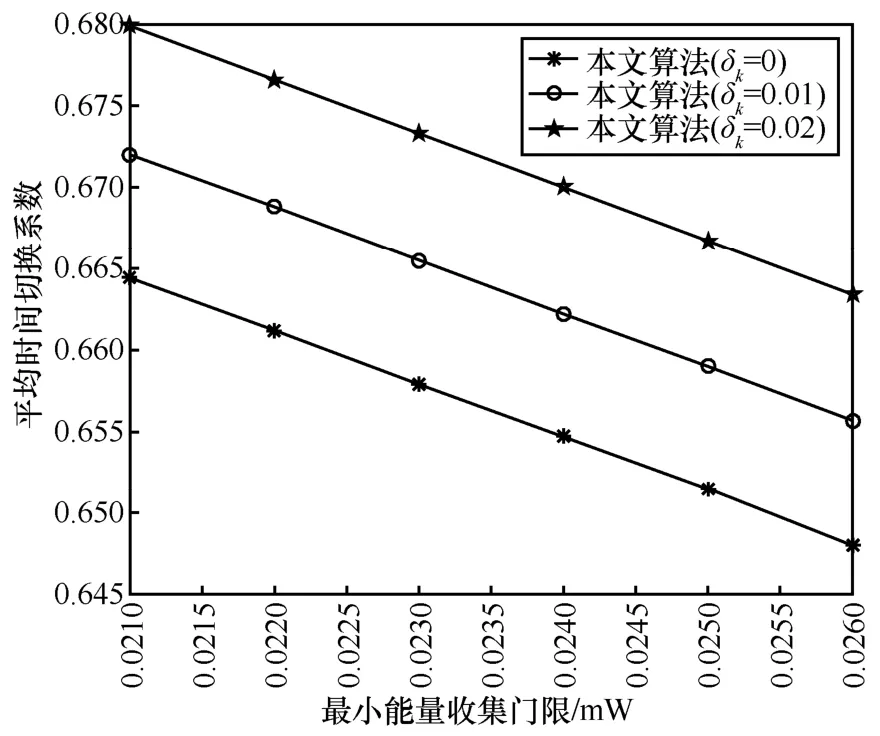
图6 平均时间切换系数与最小能量收集门限的关系

图7 给出了本文算法与传统非携能通信网络资源分配算法（without SWIPT）[23]、无线携能网络能效资源分配算法（with SWIPT）[24]在系统能效方面进行对比。仿真结果表明，本文算法具有最大的能效性能。因为本文算法同时考虑了能量收集和信道不确定性，从而使系统在保证稳健性的同时提高系统能效。另外，基于能量收集的资源分配算法（with SWIPT）系统能效高于没有考虑能量收集的传统能效资源分配算法（without SWIPT）。因为能量收集技术可以使功率消耗得到一定的补偿，从而使总的功率消耗低于传统算法（without SWIPT）。

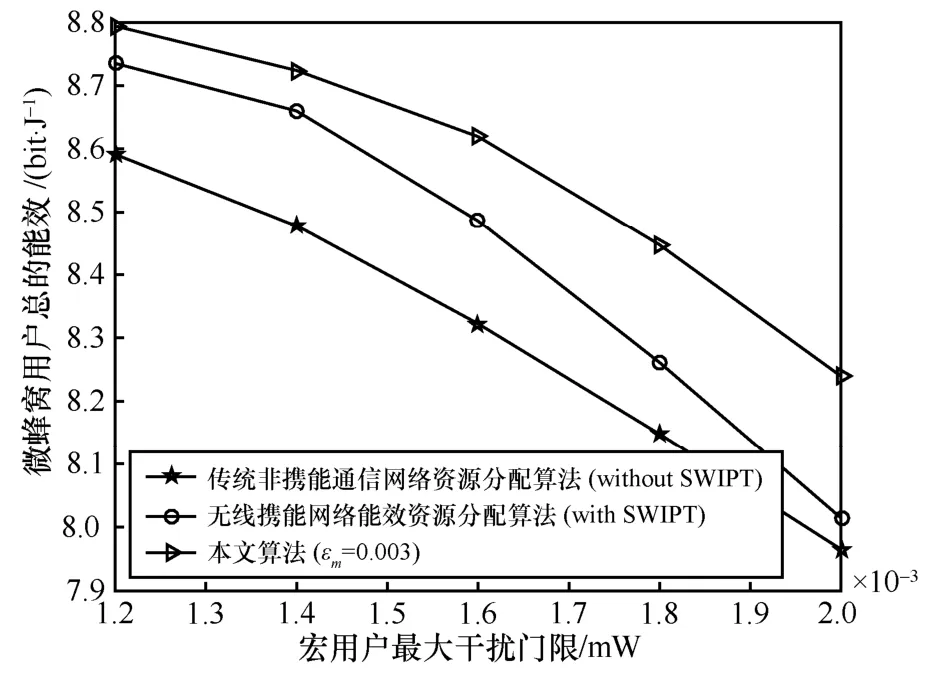
图7 不同算法的能效性能对比

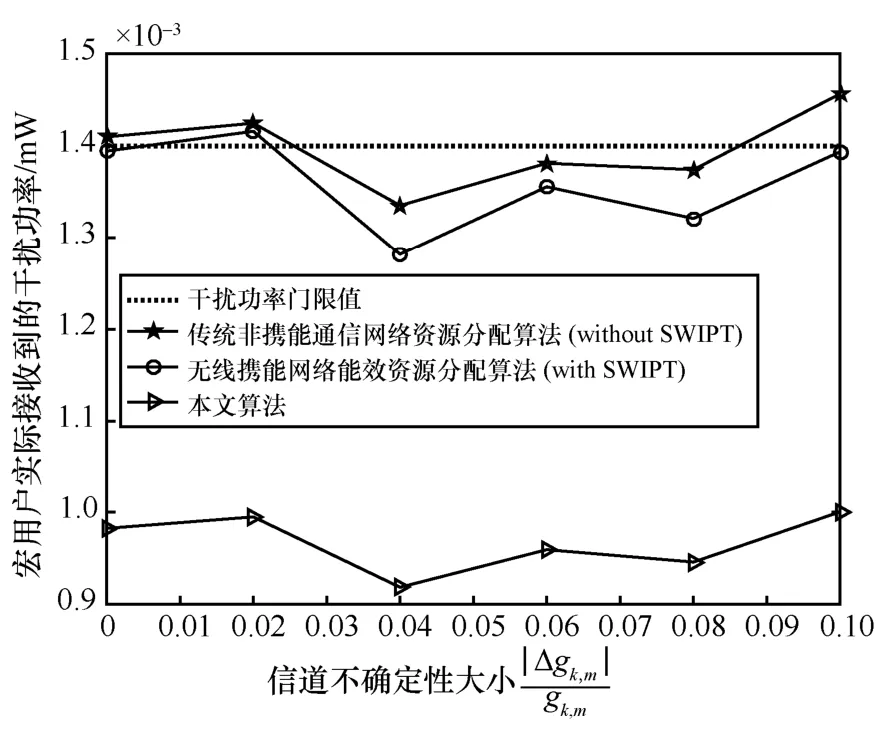
图8 给出了不同算法在随机信道不确定性下的干扰功率情况。假设干扰功率中的信道增益满足，其中gk,m=+Δgk,m，gk,m为微蜂窝网络与宏用户间的实际信道增益，为信道增益估计值，Δgk,m为估计误差，并且随机产生信道估计误差。干扰功率门限为0.001 4 mW。从图8 中可以看出，当信道增益过估计（即>gk,m）时，宏用户实际接收到的干扰功率下降。当信道增益欠估计（即

6 结束语

本文对基于NOMA 的异构携能通信网络稳健功率分配和时间优化策略进行研究。考虑用户QoS约束和最小能量收集约束，建立基于有界信道不确定性的稳健能效最大化资源分配模型。利用Dinkelbach 方法将分式目标函数转换为总数据速率与加权总能量消耗相减的形式；利用worst-case 方法和柯西不等式，将原问题转换为确定性的优化问题；根据连续凸近似方法将该问题转换为凸优化问题，利用拉格朗日对偶理论和梯度更新方法得到闭式解，并分析了算法的计算复杂度和稳健灵敏度。仿真结果表明，本文算法具有较好的稳健性和能效性能。

图8 不同算法在随机信道不确定性的干扰情况

附录1 效用函数凸凹性证明

稳健优化问题式(23)的目标函数为

显然，式(42)的第二项和第三项为关于变量{pk},∀k的线性函数。因此只需要关注第一项的凸凹性证明。第一项可以展开为

可以得到如下海森矩阵

其中，v=[v1,…,vK]T，。根据效用函数定义，显然从i=1 到i=k-1 的元素为0。定义任意非负向量Z=[Z1,Z2,…,ZK]T，则

根据柯西不等式有(XTX)(YTY)≥(XTY)2，令X=和Y=，可知ZTHZ≥ 0成立。因此海森矩阵为半正定，且f(pi)是一个凸函数，而 -f(pi)为凹函数。因此，目标函数(42)为关于变量的凹函数，存在全局最优解。

证毕。