土性参数波动范围的计算方法及影响因素

谭晓慧，杜林枫，费锁柱，侯晓亮，马海春

土性参数波动范围的计算方法及影响因素

谭晓慧，杜林枫，费锁柱，侯晓亮，马海春

（合肥工业大学资源与环境工程学院，安徽 合肥 230000）

波动范围（Scale of Fluctuation，SOF）是表征土体空间变异性的重要参数。为了探究土性参数波动范围的最优化算法及影响因素，该研究通过对比分析随机场法和地质统计学法的异同点，采用控制变量法对土性参数在不同条件下计算了SOF值，探讨了数据的趋势性、拟合参数初值、拟合点个数等因素对土性参数SOF计算结果的影响。研究结果表明：1）在利用随机场法和地质统计学法计算SOF时，去趋势化可以消除数据趋势性带来的影响，归一化可以减少不同初值对计算结果的影响。2）提出了一种同时适用于随机场法与地质统计学法的确定拟合参数初值及拟合点个数的统一方法，并在此基础上计算了某工程非饱和黏土土性参数的竖直SOF，其范围为0.14～0.62 m。研究成果可为农田的土壤改良及农田精细管理提供依据。

土壤；土体参数；空间变异性；波动范围；随机场理论；地质统计学；土力学

0 引 言

由于土体的成因类型、结构构造、地下水位、沉积条件、应力历史、风化等地质作用的差异，使得土体参数具有显著的空间变异性[1]。随着土体空间内两点之间距离的增加，参数的相关性逐渐减小。当距离大于某个值之后，参数之间的相关性可以忽略不计，此距离称作波动范围（Scale of Fluctuation，SOF）。作为描述土性参数空间变异性的重要指标，它对岩土工程的可靠度分析与设计具有重要影响[2]。

当前常用的2类分析土性参数空间变异性的方法是随机场法与地质统计学方法[3]。在随机场法方面，Vanmarcke等[4]将随机场理论引入岩土工程的可靠度分析，使用方差折减函数来表示波动范围对土体空间异性的影响，并通过积分法求解波动范围；闫澍旺等[5-6]提出了不同情况下方差折减函数的确定原则；张亚楠等[7]认为通过方差折减可以合理地表征土体参数的空间变异性；蒋水华等[8]分析了不同自相关函数类型及波动范围对边坡可靠指标的影响；田密等[9]使用贝叶斯方法结合随机场法对内摩擦角的空间变异性进行了分析。在地质统计学方面，有学者认为波动范围是半变异函数()增长到基本稳定时的滞后距[10-13]；Rezaur等[10,14-16]则通过将地质统计学法的模型转化为随机场法模型来计算波动范围；徐英等[17]将地质统计学应用在尺度效应的研究中，分析了土壤水盐的空间变异性；李建波等[18]则将地质统计学应用在温室土壤含水率与导热率的空间分布及相关性研究中。

Onyejekwe等[19]以静探数据为例，对随机场法和地质统计学法进行了对比，指出采用地质统计学方法得到的波动范围一般大于随机场法。静探数据的优点是它在深度方向上的测试结果是连续曲线，因此在竖直方向上每隔一定间距对该曲线进行离散化后，可以得到很多的数据点用于求解土体的波动范围。但是，求解其他土性参数的波动范围时，需要在钻孔中取样并进行室内试验。由于每组试验需要多个环刀土样，而每个土样的厚度至少为2 cm，因此，即使在钻孔中连续取样，能够进行的室内试验组数也相对较少[20]。此外，无论随机场法还是地质统计法，求解土体的波动范围时均需要对试验数据进行非线性曲线拟合，因此，试验个数、对试验数据的处理方法以及曲线拟合方法等因素都会影响波动范围的计算结果，而计算结果的不确定会影响后续可靠度分析的准确性，从而对实际的生产实践造成影响。

综上所述，本文对比分析了随机场法与地质统计学方法的异同点，探讨了数据的趋势性、拟合参数初值、拟合点个数等因素对土性参数波动范围计算结果的影响，提出了同时适用于随机场法与地质统计学法的确定拟合参数初值及拟合点个数的统一方法。在此基础上，以某工程的非饱和黏土为研究对象计算分析了土性参数的波动范围，验证了这一方法的可行性，为农田土壤改良及农田精细管理提供依据。

1 土体空间变异性分析方法

随机场法与地质统计学法是描述土体空间变异性的2种主要方法，二者分别以自相关函数（Auto-Correlation Function，ACF）及半变异函数（Semi-Variogram Function，SVF）来表征土体的空间变异性。因此，随机场法又称自相关函数法，地质统计学法又称半变异函数法。

1.1 随机场法与自相关函数（ACF）

随机场理论的核心思想是用方差折减函数把土体的点变异性与空间变异性结合在一起，使土体的点性质转化为空间平均性质。该理论的实质是用平稳正态随机场来模拟土体参数在空间上的变异性。因此，随机场理论要求土体参数在数学意义上符合平稳随机场的条件。平稳随机场是指随机场围绕某一均值连续地发生波动；在整个研究区域内，随机场的均值及方差为常数，且协方差函数仅与两点间的距离有关。

设土性参数平稳随机场为{(),Î}，其中，表示土性参数，它是空间位置的函数，是空间范围（距离）。记随机场的均值为，方差为2，即E(())=，Var(())=2，可以推得方差折减函数2()的表达式如下：[21]

式中σ2是随机场在空间上的平均方差；2是随机场的点方差，即0时的方差；是滞后矩(=0～)；()是点()与()的自相关函数，它是协方差函数()与点方差的比值，即

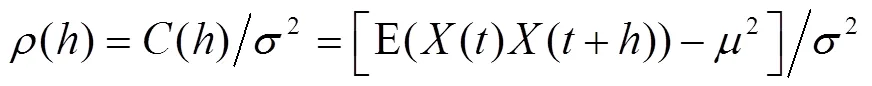
波动范围（SOF，符号记为）的计算公式如下：[5,21]

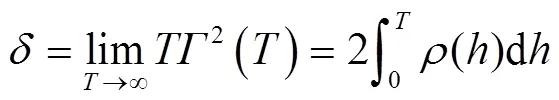
文献中亦常采用自相关距离（Auto-Correlation Distance，ACD）或自相关长度来表示土性的空间变异性[22-24]。岩土工程中常用的自相关函数模型及其对应的波动范围与自相关距离见表1[14-16,19,25-26]。表1中，模型对应的SOF值可以由式（3）积分求得，各模型对应的ACD值即为模型参数值。由表1知，除了余弦指数型ACF，其他模型的SOF与ACD值均有较大差别，但很多文献在使用SOF与ACD时并未严格区别这二者的关系[16,22,26]。

表1 常用自相关函数模型的波动范围和自相关距离

注：为滞后距，为拟合参数，(h)为自相关函数。

Note:is the hysteresis distance, andis the fitting parameter,(h) is the auto-correlation function.

1.2 地质统计学法与半变异函数（SVF）

空间岩土参数值的随机性是一种固有的随机性，它包含在岩土参数的整体空间结构之中，是结构与随机性的统一体。而地质统计学是以区域化变量为基础，借助于半变异函数（SVF）研究既具有随机性又具有结构性的自然现象的一种方法。与随机场理论相同，地质统计学理论也要求研究对象具有平稳性与正态性。

地质统计学法采用半变异函数()来表示参数的空间变异性[6,19,27-29]。半变异函数是区域化变量在点处的值()与点处的值()之差的方差的一半，即

根据方差的计算公式及二阶平稳性假设，可得

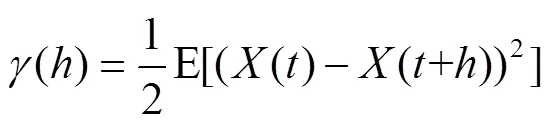
将上式的平方项展开后，进一步可以求得

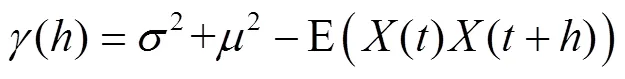
参考式（2），上式可改写为

可见，平稳随机过程()的自相关函数()与归一化后的半变异函数()/2之和为常数1。()随着的增大而减小，即随着距离的增大两点间相关性减小；()随着的增大而增大，即随着距离的增大两点间离散性增加。因此，随机场理论中的自相关函数与地质统计学中的半变异函数是采用不同的方法来表示研究对象的变异性，二者本质相同。

与ACF相似，SVF亦可用某种理论函数模型来表示。常用的SVF模型见表2，表中0为块金方差，s为结构方差；0+s为总方差。

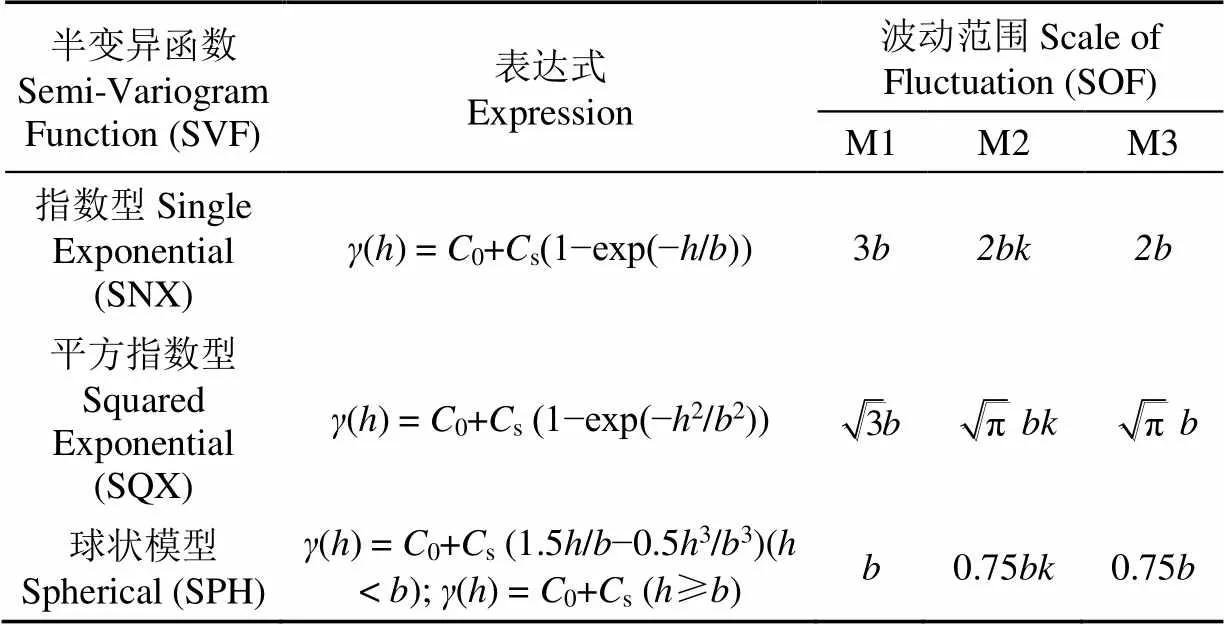
表2 常用半变异函数模型的波动范围

注：=s/(0+s)，()为半变异函数，0为块金方差，s为结构方差，M1、M2和M3为3种使用地质统计学法求解波动范围的方法。

Note:=s/(0+s),() is the semi-variogram function,0is the nugget variance,sis the structural variance, and M1, M2 and M3 are 3 methods to solve the scale of fluctuation using geostatistical methods.

在地质统计方法中常采用变程（亦称有效变程或相关程）来表示区域化变量的相关范围[6,19,27-29]。在变程之内，区域化变量具有空间相关性；在变程之外，区域变量不再相关。因此，地质统计学中的变程等同于随机场理论中的波动范围[19]。本文后续的分析中统称变程为波动范围。

在采用地质统计学法求解SOF时，文献中存在多种方法，本文将其归纳为M1、M2及M3这3种方法，其具体内容及对应的推导过程如下。

1.2.1 M1法

1.2.2 M2法

该方法先根据SVF与ACF的关系（式（7））将SVF模型转换为对应的ACF模型，再由ACF的积分求解公式（式（3））来求解SOF[27,29]。

由于距离→∞时，由式（7）知()=0，()=2；而由表2的SVF模型表达式可得当→∞时，()=0+s。因此，0+s=2。将该式代入式（7），可得

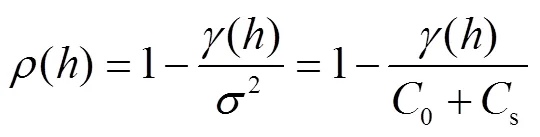
由上式可以求得表2中3种SVF模型对应的ACF的具体表达式[29]。在此基础上，可由式（3）求得对应的波动范围。因此，地质统计学法中的M2法与随机场法具有一一对应的关系。由M2法得到的SOF与SVF拟合参数的关系参见表2。

1.2.3 M3法

文献[6,19,28]采用M3法求解SOF。由表2可知M3法是M2法中取0= 0的特例。

对比表2中3种求解SOF的方法可知，当0≠ 0时，3种方法求解的SOF值各不相同。由于地质统计学法中的M2法与随机场法具有模型上的对应关系，因此，本文后续计算中如无特别说明，均采用M2法来求解土性参数的SOF值。

1.3 波动范围的计算

由上述分析可知，为了求解参数的SOF，应先对试验数据进行曲线拟合，求得曲线拟合参数，再根据表1～表2中SOF与曲线拟合参数的对应关系求解SOF，具体过程如下。

1）基于土性参数的试验数据求解ACF或SVF的估算值。对于具有个样本的空间随机过程()，由式（2）及式（5）可以得到ACF及SVF的估算值。其计算公式如下

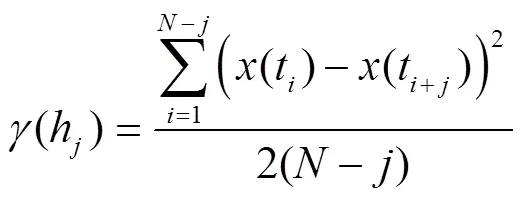
式中(t)表示t处的土性参数值；h表示点t与t之间的距离；= 0, 1, 2, …,。理论上，的最大值可取−1。但由式（9）及式（10）知，随着的增加，参与求和计算的数据对个数(−)逐渐减少，这将导致函数()或()估算值的计算误差随着或的增加而增加。因此，一般只取函数()或()的初始部分数据进行()～或()～曲线拟合。

2）采用上文提到的各种ACF或SVF模型对()～或()～数据进行非线性曲线拟合，求得模型拟合参数。本文采用科学计算语言Matlab中的lsqcurvefit函数来进行非线性曲线拟合。需要指出的是，常用的SVF拟合模型中有3个参数（0、s及），但由于0+s=2，因此，可取s=2−0，视0及为参数进行SVF参数曲线拟合。若对SVF模型进行3参数曲线拟合，将会导致错误的计算结果。

3）根据表1及表2列出的各模型SOF与拟合参数的对应关系求解相应的SOF值。

2 土性参数SOF影响因素分析

2.1 试验方法

求解土性参数的SOF值需要以试验数据为基础进行曲线拟合，因此本文分别以安徽省合肥市望江台小区施工工地触探试验（Cone Penetration Test，CPT）钻孔的试验数据及室内试验结果为例来分析土性参数SOF的影响因素。该工地土质较为单一，主要土层为黄褐色非饱和黏土，地下水位离地表约15 m。

土体的空间变异性分为竖向变异性与水平变异性，求解土体竖向SOF与水平SOF的不同点主要在于试验样本点的位置，本次只针对土体的竖向变异性进行分析。具体取样方式为分别在该场地3个钻孔中从地表下2 m处向下连续采取原状土样，再将土样分为等长的15段，每段土样长0.2 m。算例1：由该工地1个钻孔CPT试验得到锥尖阻力c与深度的关系（图1a），该组数据的个数1= 98，取样间距Δ1= 0.1m。算例2：该工地1个钻孔中非饱和土样的饱和体积含水率s与深度的关系，该组数据的个数2= 15，取样间距Δ2= 0.2 m（图1b）。算例1与2分别代表试验数据个数较多及较少的2种典型情况。这两个算例的数据来源不同，因此深度范围存在区别。

注：空心小圆圈代表原始数据点，虚线代表试验数据的趋势分量。

由于求解SOF需要对试验数据进行曲线拟合，下面分别分析试验数据的趋势性、拟合参数初值、拟合点个数等因素对SOF计算值的影响。在分析某种影响因素时，如无特别说明，其他影响因素取以下所示的基准值：1）对数据进行去趋势化处理；2）SOF的拟合初值取0.5m；3）对SVF数据进行归一化处理；4）拟合点的个数取=/2。

2.2 数据趋势性对SOF的影响

由图1知，算例1中数据c的趋势分量随着深度的增加而呈现线性增大的趋势，算例2中数据s的趋势分量则与深度无明显关系，这与文献[30]关于CPT试验数据具有趋势性而实验室物理性质指标数据无趋势性的结论一致。为了研究数据的趋势性对SOF计算值的影响，分别对未去趋势化及去趋势化后的数据求解SOF。数据去趋势化的方法是：采用线性函数拟合试验数据与深度的关系，得到原始数据的趋势分量，再将原始试验数据减去相应的趋势分量，即可得到去趋势化后的数据。通过数据去趋势化，可将原始随机场转变为零均值的平稳随机场。

数据去趋势化对SOF的影响结果见图2～图3，图中SVF数据未归一化。图2的纵坐标为ACF或SVF的估算值（()～或()～），横坐标为数据点之间的距离（）。由于算例1的试验数据具有趋势性，因此数据是否去趋势化对各种ACF及SVF模型的拟合结果均具有明显的影响。但是对于算例2，其原始试验数据与深度无明显趋势性，所以去趋势化对各ACF及SVF模型的拟合结果没有影响（图3）。后续计算为统一起见，均先对试验数据进行去趋势化处理，再求解参数的SOF。

注：ACF为自相关函数，SVF为半变异函数，横坐标“距离”指土体空间内两点距离。下同。

注：相比图b和图c，图d为进行了数据归一化处理后的结果。在图a和图d中，δ0 = 0.5 m及δ0 = 1.0 m的图形相同（δ0为SOF的初值）。

2.3 拟合参数初值对SOF的影响

2.3.1 拟合参数初值的选取

表1及表2显示的常用ACF或SVF模型均为非线性函数，而非线性曲线拟合的结果与拟合参数的初值有关。为了准确求得SOF的计算值，应尽可能合理地给定函数拟合的初值。

对于随机场法，表1中常用ACF只有1个拟合参数，它与SOF值有对应关系。因此，本文先根据经验假定SOF的初值0，再由表1中SOF的计算式反求各种ACF的拟合参数的初值（见表3）。

对于地质统计学法，表2中常用SVF有2个独立的拟合参数（0及），其中与SOF值有对应关系。由于M3法与ACF法有直接的对应关系且其SOF与0无关，因此，假定SOF的初值0之后，可根据表2中M3法的SOF计算式求得3种SVF的拟合参数的初值（见表3）。一般地，块金方差0较小，结构方差s较大。所以，为了具有普适性，根据经验，在曲线拟合时假定0= 0.1max，其中max表示参与曲线拟合的()估算值的最大值。

2.3.2 拟合结果

土体的竖直SOF一般较小，其常见范围是0.2～3.0 m[19,31]。为分析拟合参数初值对SOF计算值的影响，于常见范围中分别取SOF的初值0为0.5和1.0 m。

对于算例1，0= 0.5及1.0 m对应的拟合结果相同，ACF和SVF的拟合结果分别对应图2b 和图2d，这表明当拟合参数的初值变化不大时，参数初值对SOF的计算结果无影响。对于算例2，2种拟合参数初值对应的拟合结果见图3。可见，2种拟合参数初值（0= 0.5及1.0 m）对ACF的拟合结果无影响（图3a），但对SVF的拟合结果有明显影响（图3b及图3c）。

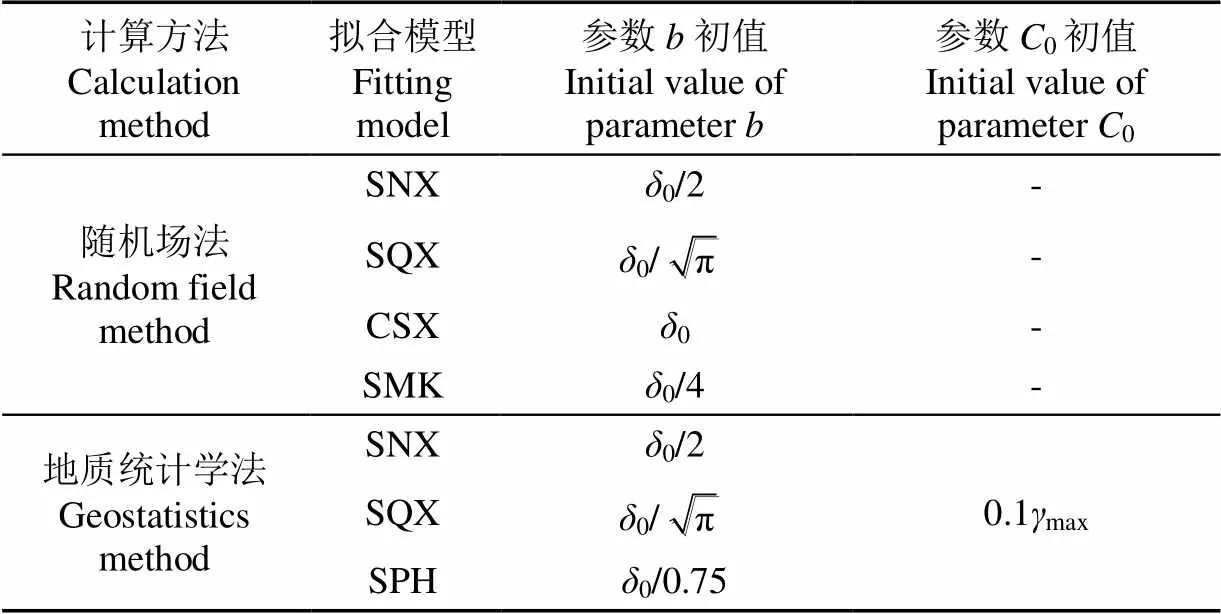
表3 拟合参数初值

注：max为参与曲线拟合的()估算值的最大值。

Note:maxis the maximum value of the estimated value of() involved in the curve fitting.

对比分析图3a、图3b及图3c的纵坐标可知，ACF与SVF的纵坐标范围值相差3个数量级。ACF的变化范围为0～1，但SVF的变化范围则为(0～1) ×10-3，该数值非常小，因此拟合参数初值的较小变化就可能导致拟合结果出现较大变化。相反，算例1中ACF与SVF的纵坐标范围值相差很小（图2），拟合参数初值的较小变化不会导致拟合结果出现较大变化。

结合式（7）可知，归一化后的SVF（即()/2）的变化范围为0～1。因此，为了减少拟合参数初值对SOF计算值的影响，本文提出如下的改进计算方法：先对SVF数据进行归一化处理，再对归一化后 SVF值进行曲线拟合。此时，2种拟合初值对应的SVF拟合结果相同（见图3d）。后续计算中，均先对SVF估算值进行归一化处理，再进行SVF函数拟合。

2.4 拟合点个数对SOF的影响

由ACF及SVF的估算公式（式（9）及式（10））可知，随着距离的增加，参与求和计算的数据对个数(−)逐渐减少，因此ACF及SVF估算值的计算误差随着的增加而增加。在进行曲线拟合时，应剔除这些误差大的数据点对计算结果的影响。

记参与曲线拟合的数据点分别为= 0, 1, 2, …,。其中，= 0表示2点之间的距离为0，=表示除去第0点后拟合点个数的最大值。文献中主要采用以下几种方法来确定拟合点的个数：取=/2[19]，=/4[6,16]及=/10[29]。由图2～图3可知，随着距离的增加，理论ACF的值由1减小为0，归一化理论SVF的值由0/2增加为1。因此，本文提出只对曲线初始段()≥0或() ≤1的数据点进行曲线拟合。各种方法的拟合结果见表4～表5，表中a行对应的数据代表本文方法的结果。

由表4及表5可见，拟合点个数对拟合相关系数2的影响较大，而对SOF的计算值则影响较小。

由于原始数据来源不同，多种取拟合点个数的方法产生了不同的结果。对于算例1（试验点个数较多），本文方法与=/10对应的2及SOF较为一致，这2种方法的2明显大于/2及/4。对于算例2（试验点个数较少），/2对应的2和SOF明显小于其他3种方法；对于多数拟合模型，本文方法与/4对应的2及SOF值较为一致。这体现了当数据点较多时，取大量拟合点会引入误差较大的部分数据，而当数据点较少时，取=/10会造成只对极少的数据点进行拟合，从而失去实际意义。

表4 拟合点个数对拟合相关系数及SOF的影响（算例1）

注：代表全部的数据点个数，代表参与拟合的数据点个数，a代表本文方法的数据点个数。

Note:represents the number of all data points,represents the number of data points participating in the fitting, andarepresents the number of data points of the method presented in this paper.

表5 拟合点个数对拟合相关系数及SOF的影响（算例2）

上述2个典型算例的对比分析表明，当试验点个数较多时，取/10较为合理；当试验点个数较少时，取/4较为合理。而本文方法则可同时适用于这2个典型算例。因此，本文的方法具有更广泛的适用性。

2.5 求解SOF的计算条件

通过本节的影响因素分析，确定求解SOF的计算条件为：1）对试验数据进行去趋势化处理，从而消去数据的趋势性对计算结果的影响；2）对SVF数据进行归一化处理，以便消去数值的数量级差距对SVF数据的影响；3）只对曲线初始段()≥0或()≤1的数据点进行曲线拟合。

3 两类方法波动范围的对比分析

在第2节确定的SOF计算条件下，可求得表1及表2中各种模型对应的SOF值。由于常用的ACF及SVF模型都含有单指数型（Single Exponential，SNX）及平方指数型（Squared Exponential，SQX），下面以这2种模型为例进行SOF的对比分析。2个算例的SOF值及曲线拟合决定系数2见表6。

由表6可见，2个算例SNX模型对应的SOF均大于SQX模型。对于SNX模型，SVF-M1方法的SOF明显大于其他3种方法，而其他3种方法的SOF在算例1中几乎相等，算例2中ACF方法的SOF明显小于其他3种方法；对于SQX模型，算例1中各种方法的SOF基本相等，算例2中，3种SVF方法的SOF均大于ACF方法。

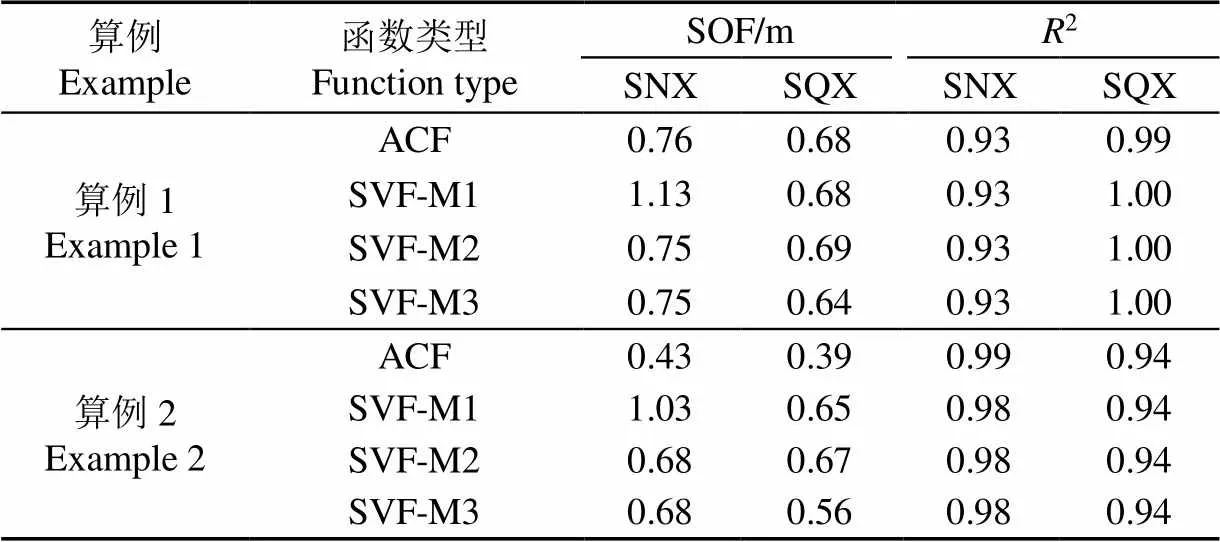
表6 SOF和拟合相关系数的对比分析

算例1中SNX模型的2均小于SQX模型，而算例2中的规律恰好相反。

2个算例的对比分析表明：1）对于同一种拟合模型，ACF与SVF的SOF没有固定的相对大小关系；2）土性参数的SOF值与计算方法及拟合模型有关；3）不同的拟合模型适用于不同的试验数据，没有一种拟合模型始终优于另一种拟合模型。

4 非饱和土性质参数的波动范围

4.1 试验土样土性参数

对2.1节中工地所取的土样进行室内试验，测定非饱和土样的基本物理性质指标及土水特征指标。其中，基本物理性质指标包括含水率、密度及颗粒相对密度s，土水特征指标指土水特征曲线（Soil-Water Characteristic Curve，SWCC）的拟合参数。本文采用van Genuchten模型[32]来表示SWCC，其拟合参数为VG、VG及饱和体积含水率s，以1#钻孔为例，土性参数的试验数据见表7。

表7 土性参数试验结果（1#）

4.2 土性参数的波动范围

在2.5节总结的计算条件下，对3个钻孔的试验数据进行计算，可得出土体各参数的波动范围。以SNX及SQX模型为例，ACF及SVF这2类方法对应3个钻孔各指标SOF的均值见表8（此处的均值是指对3个钻孔中同一指标的SOF取平均值）。

表8 土性参数的波动范围（SOF）

由表8可见，合肥地区非饱和黏土竖直方向上的SOF范围处于0.14～0.62 m，并且对于同一种计算方法及函数模型，土体各性质参数的SOF的变化范围无明显区别。但是，采用随机场法即ACF求得的土体SOF略小于采用地质统计学法即SVF求得的相应值。例如，对于ACF法，采用SNX及SQX模型得到的土体SOF值分别为0.15～0.51 m及0.14～0.45 m，二者的范围大致相同；对于SVF法，采用SNX及SQX模型得到的土体SOF值分别为0.19～0.62 m及0.24～0.61 m，二者的范围亦大致相同，但它们略大于随机场法（ACF）的SOF值。

5 结 论

本文对比分析了求解土性参数波动范围（Scale of Fluctuation， SOF）的随机场法与地质统计学法，探讨了数据趋势性、曲线拟合参数初值及拟合点个数等因素对波动范围计算结果的影响，并计算了某工程场地非饱和黏土性质参数的波动范围。主要结论如下：

1）随机场法与地质统计学法分别采用不同的理论来研究土性参数的空间变异性。由于地质统计学法中的M2方法是将SVF（Semi-Variogram Function，半变异函数）模型转换为ACF（Auto-Correlation Function，自相关函数）模型，2种方法计算得到的波动范围有一一对应关系。

2）在地质统计学法中对半变异函数进行曲线拟合时，应先对SVF估算值进行归一化处理，这样可以减少曲线拟合参数的初值对计算结果的影响。

3）提出了确定曲线拟合参数初值及拟合点个数的统一方法，该方法可同时适用于随机场法与地质统计学法。

4）以某工程的非饱和黏土为研究对象，在试验研究的基础上使用ACF法和SVF法求得了土体物理性质参数及水力参数的竖向波动范围，结果表明：土体各性质参数的SOF无明显区别；采用随机场法求得的土体SOF略小于采用地质统计学法。

5）合肥地区非饱和黏土竖直方向上的SOF范围处于0.14～0.62 m。

[1]刘晓，唐辉明，熊承仁. 边坡动力可靠性分析方法的模式、问题与发展趋势[J]. 岩土力学，2013，34(5)：1217-1234. Liu Xiao, Tang Huiming, Xiong Chengren. Patterns, problems, and development trends of analysis methods for slope dynamic reliability[J]. Rock and Soil Mechanics, 2013, 34(5): 1217-1234. (in Chinese with English abstract)

[2]Deutsch C V, Journel A G. Geostatistical software library and user’s guide[J]. Technometrics, 1998, 40(4): 357-357.

[3]高大钊. 岩土工程设计安全度指标及其应用[J]. 工程勘察，1996(1)：1-6. Gao Dazhao. Safety index of geotechnical engineering design and application[J]. Geotechnical Investigation & Surveying, 1996(1): 1-6. (in Chinese with English abstract)

[4]Vanmarcke E H. Probabilistic modeling of soil profiles[J]. Journal of Geotechnical Engineering Division, ASCE, 1977, 103(11): 1227–1246.

[5]闫澍旺，朱红霞，刘润. 关于随机场理论在土工可靠度计算中应用的研究[J]. 岩土工程学报，2006，28(12)：2053-2059. Yan Shuwang, Zhu Hongxia, Liu Run. Study on application of random field theory to reliability analysis[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2053-2059. (in Chinese with English abstract)

[6]朱红霞，闫澍旺. 天津港地基土随机场特性及可靠度分析[J]. 岩石力学与工程学报，2007，26(S2)：3959-3965. Zhu Hongxia, Yan Shuwang. Random field model and reliability analysis of foundation soil in Tianjin port[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S2): 3959-3965. (in Chinese with English abstract)

[7]张亚楠，曹子君，高国辉，等. 考虑土体参数空间变异性的浅基础扩展式可靠度设计[J]. 武汉大学学报：工学版，2018，51(9)：753-759. Zhang Ya’nan, Cao Zijun, Gao Guohui, et al. Expanded reliability-based design of shallow foundations in spatially variable soils[J]. Engineering Journal of Wuhan University, 2018, 51(9): 753-759. (in Chinese with English abstract)

[8]蒋水华，李典庆，周创兵，等. 考虑自相关函数影响的边坡可靠度分析[J]. 岩土工程学报，2014，36(3)：508-518. Jiang Shuihua, Li Dianqing, Zhou Chuangbing, et al. Slope reliability analysis considering effect of autocorrelation functions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 508-518. (in Chinese with English abstract)

[9]田密，李典庆，曹子君，等. 基于贝叶斯理论的土性参数空间变异性量化方法[J]. 岩土力学，2017，38(11)：3355-3362. Tian Mi, Li Dianqing, Cao Zijun, et al. Quantification of spatial variability of soil parameters using Bayesian approaches[J]. Rock and Soil Mechanics, 2017, 38(11): 3355-3362. (in Chinese with English abstract)

[10]Rezaur R B, Rahardjo H, Leong E C. Spatial and temporal variability of pore-water pressures in residual soil slopes in a tropical climate[J]. Earth Surface Processes and Landforms, 2002, 27(3): 317-338.

[11]Liao K H, Xu S H, Wu J C, et al. Assessing soil water retention characteristics and their spatial variability using pedotransfer functions[J]. Pedosphere, 2011, 21(4): 413-422.

[12]Wang Y Q, Shao M A, Han X W, et al. Spatial variability of soil parameters of the van Genuchten model at a regional scale[J]. CLEAN - Soil, Air, Water, 2015, 43(2): 271-278.

[13]Taskinen A, Sirviö H, Bruen M. Generation of two-dimensionally variable saturated hydraulic conductivity fields: Model theory, verification and computer program[J]. Computers & Geosciences, 2008, 34(8): 876-890.

[14]Stuedlein A W, Kramer S L, Arduino P, et al. Geotechnical characterization and random field modeling of desiccated clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(11): 1301-1313.

[15]Uzielli M, Lacasse S, Nadim F, et al. Soil variability analysis for geotechnical practice[C]// Proceedings of the 2nd International Workshop on Characterisation and Engineering Properties of Natural Soils. London: Taylor & Francis Group, 2006.

[16]Phoon K K, Quek S T, An P. Identification of statistically homogeneous soil layers using modified bartlett statistics[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 129(7): 649-659.

[17]徐英，陈亚新，史海滨，等. 土壤水盐空间变异尺度效应的研究[J]. 农业工程学报，2004，20(2)：1-5. Xu Ying, Chen Yaxin, Shi Haibin, et al. Scale effect of spatial variability of soil water-salt[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(2): 1-5. (in Chinese with English abstract)

[18]李建波，王卫华，Su Yiming，等. 温室土壤含水率与导热率空间分布及相关性[J]. 农业工程学报，2016，32(19)：127-132. Li Jianbo, Wang Weihua, Su Yiming, et al. Spatial pattern and interrelation of soil water content and thermal conductivity in greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(19): 127-132. (in Chinese with English abstract)

[19]Onyejekwe S, Kang X, Ge L. Evaluation of the scale of fluctuation of geotechnical parameters by autocorrelation function and semivariogram function[J]. Engineering Geology, 2016, 214: 43-49.

[20]Tan X H, Li P, Shen M F, et al. Evaluation of the spatial variability characteristics of the unsaturated clay in Hefei, China[J]. Soils and Foundations, 2020, 60(2): 454-465.

[21]Vanmarcke E. Random Fields, Analysis and Synthesis[M]. Cambridge, Mass: MIT Press, 1983.

[22]Srivastava A, Babu G L S, Haldar S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis[J]. Engineering Geology, 2010, 110(3/4): 93-101.

[23]谭晓慧，胡晓军，吴坤铭. 同时考虑基本变量和极限状态模糊性的边坡模糊随机有限元可靠度分析[J]. 岩石力学与工程学报，2009，28(S2)：3952-3958. Tan Xiaohui, Hu Xiaojun, Wu Kunming. Fuzzy random finite element reliability analysis of slope stability with fuzzy basic veriables and fuzzy states[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3952-3958. (in Chinese with English abstract)

[24]Cho S E, Park H C. Effect of spatial variability of cross-correlated soil properties on bearing capacity of strip footing[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(1): 1-26.

[25]蒋水华，李典庆，周创兵，等. 考虑自相关函数影响的边坡可靠度分析[J]. 岩土工程学报，2014，36(3)：508-518. Jiang Shuihua, Li Dianqing, Zhou Chuangbing, et al. Slope reliability analysis considering effect of autocorrelation functions[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 508-518. (in Chinese with English abstract)

[26]Zielli M U, Vannucchi G, Hoon K K P. Random field characterisation of stress-nomalised cone penetration testing parameters[J]. Géotechnique, 2005, 55(1):3-20.

[27]Elkateb T, Chalaturnyk R, Robertson P K. An overview of soil heterogeneity: Quantification and implications on geotechnical field problems[J]. Canadian Geotechnical Journal, 2003, 40(1): 1-15.

[28]Meek D W. A semiparametric method for estimating the scale of fluctuation[J]. Computers & geosciences, 2001, 27(10): 1243-1249.

[29]王建锋. 用地质统计学计算土层相关尺度[J]. 土木工程学报，2005，38(10)：102-107. Wang Jianfeng. Estimation of autocorrelation distance of soil properties by using geostatistics[J]. China Civil Engineering Journal, 2005, 38(10): 102-107. (in Chinese with English abstract)

[30]张继周，缪林昌，陈俊波. 苏中腹地湖相软土土性参数变异性统计描述[J]. 岩土力学，2010，31(2)：471-477. Zhang Jizhou, Miu Linchang, Chen Junbo. Statistical characterization of variability of lacustrine soft soil in central region of Jiangsu Province[J]. Rock and Soil Mechanics, 2010, 31(2): 471-477. (in Chinese with English abstract)

[31]Phoon K K, Kulhawy F H. Characterization of geotechnical variability[J]. Canadian geotechnical journal, 1999, 36(4): 612-624.

[32]Sillers W S, Fredlund D G. Statistical assessment of soil-water characteristic curve models for geotechnical engineering[J]. Canadian Geotechnical Journal, 2001, 38(6): 1297-1313.

Calculation method and influence factors for fluctuation scale of soil parameters

Tan Xiaohui, Du Linfeng, Fei Suozhu, Hou Xiaoliang, Ma Haichun

(,230000,)

Soil properties vary randomly from location to location, due mainly to different genetic types, geologic structures, depositional conditions, stress history, and weathering conditions. Serving as a key parameter to describe the spatial variability, the Scale of Fluctuation (SOF) can be defined as the minimum distance within which a significant correlation exists among soil properties. Specifically, the spatial fluctuation of soil parameter decreases with the increase of the SOF. The SOFs of soil properties is also critical to the reliability analysis on geotechnical structures. The random field and geostatistical methods are commonly used to calculate the SOF of soil properties. In this study, a theoretical derivation was conducted to comparatively analyze the Auto-Correlation Function (ACF) in the random field method, the Semi-variance Function (SVF) in the geo-statistical method, and the corresponding SOFs. Two typical cases (one has many test data, and another has very limited test data) were selected to explore the influences of the trend in the test data, the initial values of curve fitting parameters, and the number of fitting data, on the calculated SOFs for the random field and geo-statistical method. The results demonstrated that the random field and geo-statistical method were essentially the same, and a clear one-to-one relationship was found in the ACF of random field method, and the SVF of M2 method in the geo-statistics method. It infers that the test datum can be detrended before they were used for calculating the SOFs. Prior to the curve fitting for the SOFs of soil properties, the estimated SVF can firstly be normalized. A unified approach was also proposed to determine the initial values of curve fitting in the random field and geo-statistical method, particularly from the experience values of SOFs for soil properties. The optimum number of fitting data was determined for the ACF and the SVF. In calculating the SOFs of soil parameters, it needed to consider only the first several estimated ACFs greater than or equal to zero, and that of SVFs less than or equal to one. In calculating the vertical SOFs of soil parameters, several laboratory tests were conducted for an unsaturated clay, where soil samples were vertically taken from three bore holes. Three physical parameters (water content, density, and specific density of soil particles), three fitting parameters (,ands) of Soil Water Characteristic Curve (SWCC) in the van Genuchten model, , and then the SOFs of all these soil parameters were calculated using the random field and geo-statistical method. The values of SOF for these soil properties of unsaturated clay were 0.14-0.51 m in the random field method, and 0.19-0.62 m in the geo-statistical method, indicating that the calculated SOFs from the random field method were a relatively smaller than those from the geo-statistical method.

soils; soil parameters; spatial variability; scale of fluctuation; random field theory; geostatistics; soil mechanics

谭晓慧，杜林枫，费锁柱，等. 土性参数波动范围的计算方法及影响因素[J]. 农业工程学报，2020，36(24)：91-98.doi：10.11975/j.issn.1002-6819.2020.24.011 http://www.tcsae.org

Tan Xiaohui, Du Linfeng, Fei Suozhu, et al. Calculation method and influence factors for fluctuation scale of soil parameters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(24): 91-98. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.24.011 http://www.tcsae.org

2020-09-21

2020-12-10

国家自然科学基金资助项目（41972278）

谭晓慧，博士，教授，主要从事岩土工程的可靠度分析与概率极限状态设计方面的研究。Email：tantan9666@126.com

10.11975/j.issn.1002-6819.2020.24.011

TU43

A

1002-6819(2020)-24-0091-08