自适应航天器态势分析系统

雷宇田,杨嘉琛,满家宝,奚 萌

(天津大学电气自动化与信息工程学院,天津 030072)

0 引言

在21世纪各国激烈竞争与博弈的环境之下,航天器相关技术起到了相当重要的作用。而对航天器的姿态及位置偏移量等信息的有效测量,在航天器的组装及发射过程中至关重要。能够在短时间内快速、准确地测量出航天器姿态和距离偏移量,并进一步实现精准矫正与控制也成为了航天器在组装及发射前的必然要求。

与此同时,现今国内外军事应用领域所使用的航天器组装及发射中的态势测量与分析系统精度较低,与偏移矫正系统误差较大,这些问题严重制约了航天器组装及发射过程中的精准化测量,可能导致在组装过程中出现损耗等问题,进而引发潜在的应用风险。

国内外许多学者都对此展开了研究,而基于单目视觉装置的位置与姿态测量方案取得了较好的测量效果。在国内最新提出的三维姿态角测量方案中,苏建东等[1]于2017年提出了基于单目视觉和棋盘靶标的平面姿态测量方法,利用棋盘靶标标定摄像机,然后利用Givens矩阵分解外参矩阵,求取姿态角。张浩鹏等[2]提出了基于姿态加权核回归的航天器姿态估计,通过对视觉输入的核函数进行加权学习姿态特征。在利用卷积神经网络估计物体姿态方面,王松等[3]进行了基于卷积神经网络(CNN)的深度图姿态估计算法研究,利用深度图像和线性回归估计姿态函数。

在基于三轴陀螺仪和其他相关测量仪器的位姿测量和解算方面,吴涛等[4]提出了基于卡尔曼滤波的航姿参考系统设计,利用三轴陀螺仪测量姿态四元数,然后利用卡尔曼滤波算法将三轴磁传感器与三轴加速度计的数据进行融合,从而修正姿态四元数,提高解算精度。张力军等[5]提出了基于欧拉角观测模型的航天器姿态确定方法,通过研究基于欧拉角的观测模型,证明了原灵敏度矩阵的缺陷,推导出了正确的矩阵形式并进行了数据仿真。刘转等[6]提出了导向轴姿态测量方法研究,利用三轴重力加速度记采集导向轴的姿态信息,设计出一套基于导向轴的姿态测量系统并继续了模拟实验。

但这些方案仍未摆脱传统的基于单目视觉的位姿测量对图像的高精度获取要求,且使用条件较为严苛,在一定程度上限制了位置与姿态测量的准确性。因此,一个能够降低对测量设备及环境的依赖和降低解算法复杂度的姿态角测量方法显得尤为重要。

基于以上研究及发展现状,本文首次利用深度学习中的卷积神经网络理论,基于单目视觉系统,拍摄已贴放特定标识物的航天器影像,通过分析航天器影像数据,实现对航天器运输及发射过程中航天器的三维姿态角、距拍摄点距离以及位置相对拍摄中心偏移量的态势精准测量与自适应分析。

1 模型的建立及样本的获取

1.1 算法思路概述

本文采用的卷积神经网络算法的输入为六维模型的平面图,输出为该六维模型的姿态参数。采用的模型是对姿态参数进行估计的回归模型,输出的参数是连续的。

本文的卷积神经网络的结构借鉴了主流网络结构,利用控制变量法探究神经网络的学习率、损失函数、激活函数及网络结构等来优化目标函数。本文算法分为训练阶段和测试阶段进行。训练阶段中,用训练集中的图像作为卷积神经网络的输入,输出为相应的姿态和位置参数,由此训练了一个合适的卷积神经网络模型。测试阶段中,使用测试集中的图像作为卷积神经网络的输入,经过预先训练的卷积神经网络模型后得到相应的姿态和位置参数输出,并与其本身的的标签进行比较,以此来判断姿态和位置参数估计网络的质量。

1.2 训练及测试样本获取

考虑到在位置和姿态角测量中,搭建实际环境的难度较高,花费的时间过长、费用较高,且安装精度难以控制,会对本文的测量精度产生一定影响,而且卷积神经网络的训练需要大量不同位置和姿态角的图片作为训练样本,因此实验采用在PC端仿真的方法来实现对实验模型的搭建以及全部样本的获取。

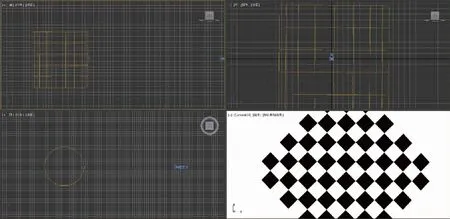
图1 3d Max模型示意图Fig.1 The model in 3d Max

训练及测试样本全部由3dMax软件仿真得到。本文用3dMax建立了一个圆柱体模型用来模拟航天器的主体部分,并在主体侧面贴放了合适大小的标志物。本次实验选取航天器主体半径为1m,高度为2m,标识物为半径0.8m的黑白棋盘格[7],并将圆柱体表面颜色设置为白色。为了使目标物在滚转角和偏航角的转动特征更加明显,本文将水平的棋盘格旋转45°,改为竖直放置,从而增加其边缘信息的复杂度,有效地增加边缘复杂度能够使神经网络学习到更多的变化特征。实验证明,将标识物旋转放置的确可以使网络对其在相机拍摄面上的运动测量精度上升。棋盘格图样及贴放方式如图1所示。随后引入摄像机,将其与目标物主体的距离设置为6m,即距标识物5m。调整摄像机焦距与标识物对焦,并适当调整摄像机的视野范围,使标识物可以占据拍摄图片的绝大多数区域,同时保证在目标物带动标识物进行位移、旋转的过程中不会使目标物超出相机拍摄范围。

将目标主体沿x、y、z轴方向的位移状态定为[abc]。由于视角问题,将航天器的俯仰角定义为d,偏航角定义为e,滚转角定义为f。样本六维姿态取值范围如表1所示。

表1 取值范围表

为模拟实际需要,设置沿轴方向位移的步长均为0.01m,三个旋转角度的步长均为0.01°。由此可得不同的样本一共有1013×113=1371330631种,由此必须采用随机数组来生成所需的样本图片。为了避免生成随机数时的正态分布情况,借助MATLAB中的unidrnd()函数,在6个维度生成均匀随机分布的随机数,以此来实现图片样本在6个维度上各自范围内的均匀随机分布,防止一般随机函数的正态分布效应影响训练结果。

用3dMax自带脚本语言编写脚本文件,将生成的5万组随机数导入到脚本文件中,随后均匀随机生成样本5万张,作为实验的基础样本。

基于3dMax生成的基础样本以连续的数字序列命名,对其进行标签化处理,以此和生成的随机数组一一对应，最终形成实验的训练集和测试集。

1.3 卷积神经网络架构搭建

1.3.1 卷积神经网络的优势

本文选择卷积神经网络而没有使用传统神经网络的原因是在特征提取方面,卷积神经网络和传统神经网络有很大的不同。卷积神经网络利用局部连接和权值共享的方法优化特征提取,减少神经网络训练所需的参数数量[8]。

1)局部连接是神经网络中某一层的神经元只连接上一层中一部分的神经元,而不进行全连接。传统神经网络采用全连接,随着图片的增大和网络深度的增加,参数会成指数级增加。而局部连接可以让神经网络的参数大为减少,同时不受图片大小的影响。

2)权值共享是赋予所有神经元相同的参数。如果针对每一个神经元都训练一套参数,且隐藏层神经元个数较多,就会导致全局需要海量参数,非常不便于训练。但是参数权值共享的方法可以让全局的神经元使用同一套参数,大大减少了所需训练的参数与数量,同时也减少了所需的存储空间。

1.3.2 卷积神经网络的概要

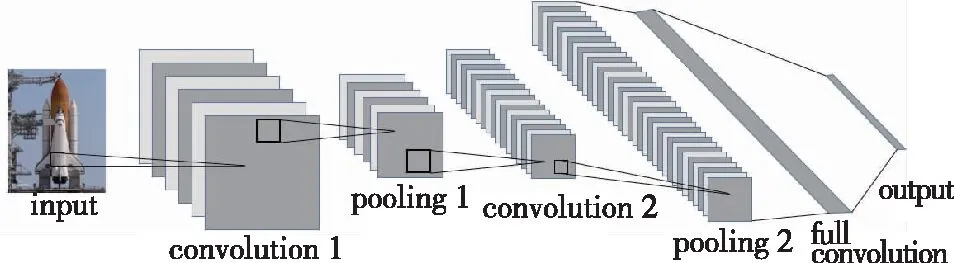
图2 卷积神经网络示意图Fig.2 Convolutional neural network

卷积神经网主要包括输入层、卷积层、池化层、全连接层和输出层,同时也需要对激活函数和损失函数等进行设置。

卷积层是对上一层的图片进行卷积操作,相当于用一个滤波器对图像进行滤波,生成相对应的特征图(feature map)。

池化层又称为采样,最常用的是最大值采样,目的是通过采样来减少特征值,也就减少了计算量,并且还减小了训练期间过拟合的可能性。而为了进一步解决过拟合的问题,现在通常使用dropout(随机丢弃网络节点)方法,可以使神经元随机失活,从而降低神经元之间的相互依赖性。

激活函数为整个网络提供非线性的拟合,提高神经网络模型的复杂程度,使其可以逼近任意函数。一般常用的激活函数有sigmoid、tanh、ReLU和ELU等函数。

sigmoid函数的表达式为

(1)

式中,e是自然常数,其值为2.71828；z是自变量,取值范围为全体实数集。对应表达图像如图3所示。

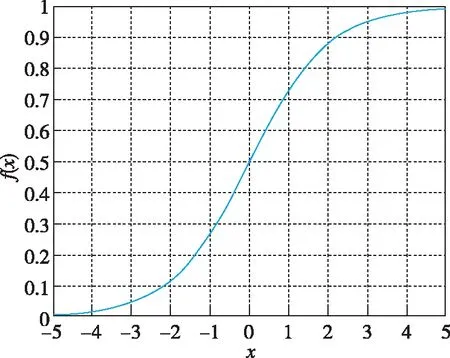
图3 Sigmoid函数图像Fig.3 Sigmoid function

tanh函数的表达式为

(2)

该函数为奇函数,当输入z小于0时,取值范围为[-1,0]；当输入z大于0时,取值范围为[0,1]。其对应表达图像如图4所示。

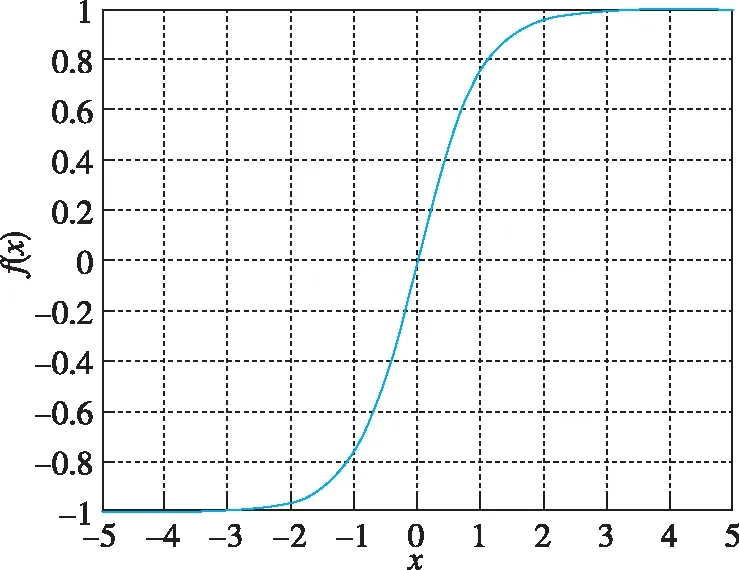
图4 tanh函数图像Fig.4 tanh function

Sigmoid函数将输入的任意值压缩至0～1的范围内,但在绝对值较大的地方梯度比较平缓,同时它的输出也不是0均值。tanh函数可以看作是sigmoid函数的改进版,但只改进了输出均值不为0的问题。由于绝对值大的地方梯度平缓,Sigmoid函数和tanh函数均存在梯度消失的问题。ReLU函数是目前最为常用的激活函数,很好地避免了梯度消失的问题,同时由于它的正半轴是线性函数,所以计算速度和收敛速度都非常快。但ReLU函数也有缺点——负半轴输出均为0，这会导致某些神经元永远不会被激活,造成网络大面积坏死。而ELU函数针对这个问题做了改进,在负半轴有一定的输出，但负半轴的输出一样存在梯度饱和的问题。

ReLU函数的表达式为

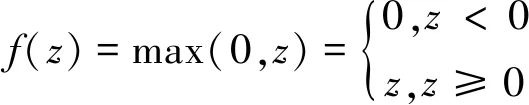
(3)

其对应表达图像如图5所示。

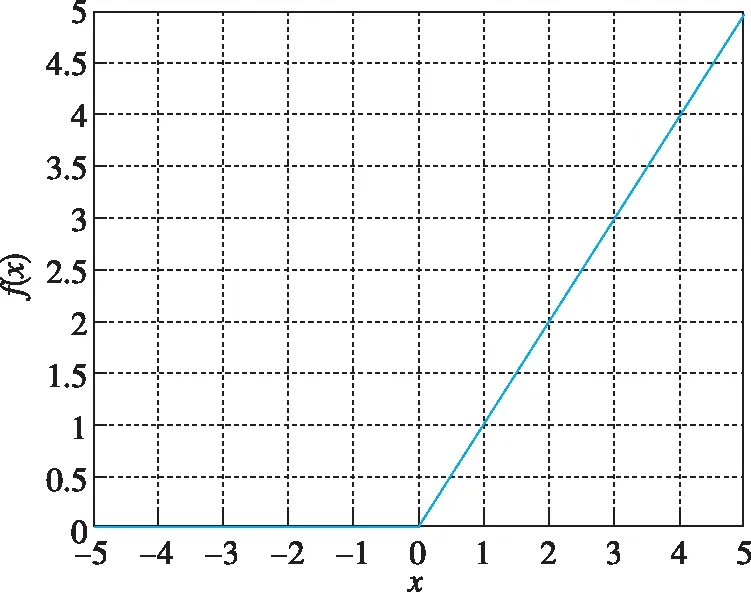
图5 ReLU函数图像Fig.5 ReLU function

ELU函数的表达式为

(4)

式中,α是一个大于0的参数,用于调节该函数在z≤0时的函数形状。其对应表达图像如图6所示。

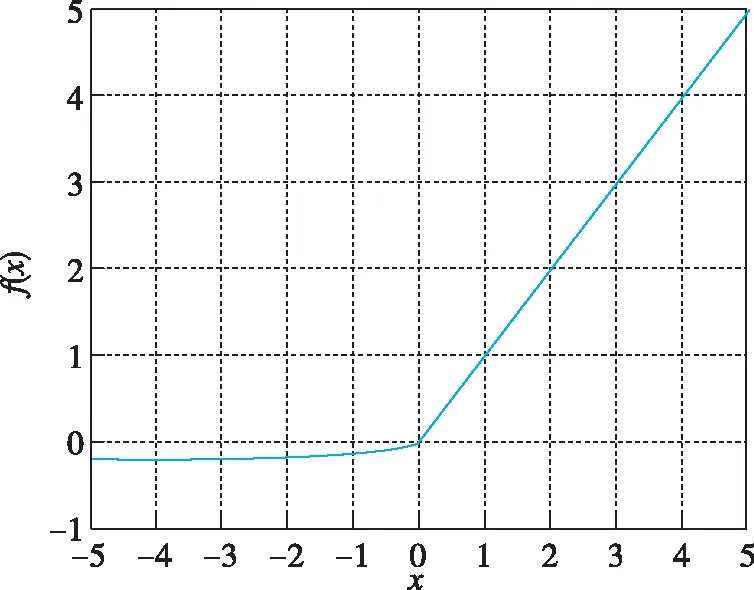
图6 ELU函数图像Fig.6 ELU function

1.3.3 神经网络模型

由于传统的浅层神经网络已经能够进行较好地非线性表达,故本文选用了9层神经网络结构，如图7所示。由于服务器计算能力有限，故本文输入层选用512×256的图片。由于本文选用了黑白棋盘格作为标识物,位置和姿态参数估计主要依靠卷积神经网络所提取的边缘信息特征,于是选用了最为常用的大小为3×3的卷积核[9-10],同时采用最大值池化,池化层核的大小为2×2，这可以较为显著地减小计算量。如前所述,本文对于位置和姿态参数的估计是一个回归问题,所以最后一层激活函数应选择Linear函数,对应的表达式为

f(z)=az

(5)

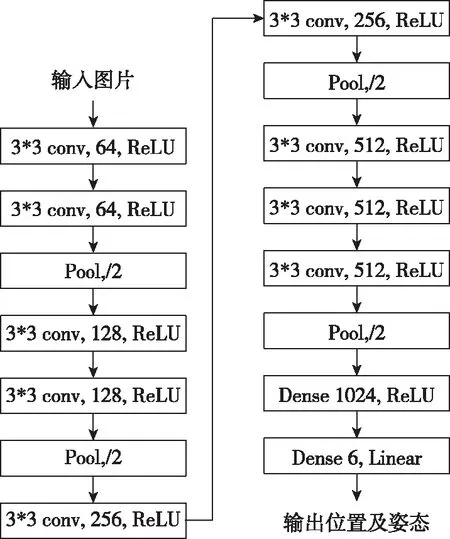
图7 卷积神经网络架构Fig.7 CNN structure

本文使用的损失函数是均方根误差(MSE),它的含义是计算同一类别中所有样本的估计值与其预测值的欧氏距离平方的均值

(6)

如果模型预测的结果与实际值的误差满足正态分布,那么这个假设就是合理的。

2 实验结果

本文实验分为以下几个步骤：1)利用3dMax软件生成本文所需数据集；2)对训练集和测试集进行标签化和预处理；3)将样本集和标签投入网络,训练合适的神经网络权重模型；4)用训练好的模型预测测试集的位置和姿态输出，并与标签进行比较,分析误差。

本文训练所需样本的获取及标签化如前所述。对样本集和测试集做相同的数据预处理。因电脑的存储能力限制,本文将原始生成的640×640大小的图片变换大小到256×512。这是一个常用的图片大小[11],本文以此作为基准进行对比实验。由于服务器性能等原因,使用训练50轮为基准进行对比实验,因为当网络训练至50轮时，该卷积神经网络已经可以收敛至一个相对较优的结果。

为探究不同网络对位置和姿态参数估计的影响并确定适用于实验的神经网络,本文选用了9层卷积神经网络,15层卷积神经网络,50层的ResNet网络,152层的ResNet网络和DenseNet网络进行对比试验。不同网络训练得出的位置和姿态的平均误差表如表2所示。(位置误差单位为m,角度误差单位为(°),下同)

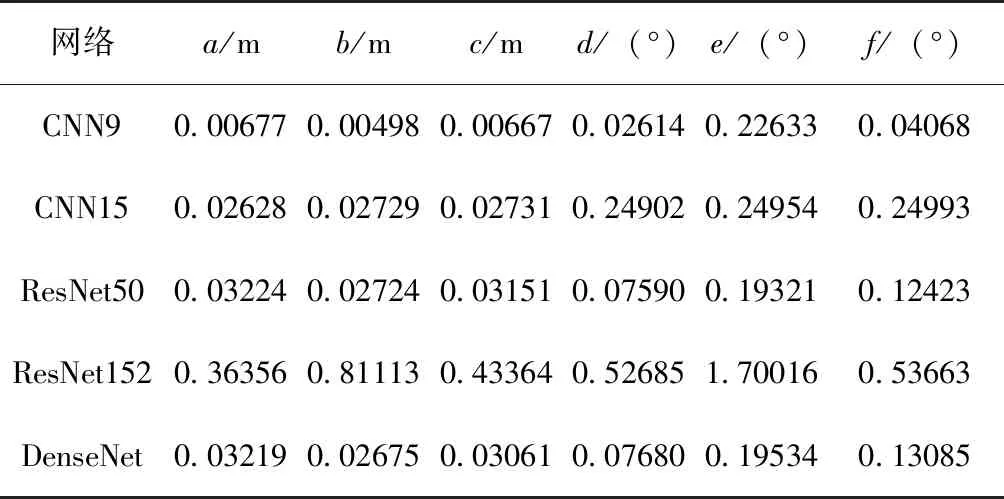
表2 不同网络的六维度平均误差

相对于简单卷积网络CNN，深度残差网络ResNet具有更深的网络结构,但也不会产生将CNN直接加深后导致的梯度消失和梯度爆炸现象。在此基础上,密集连接卷积网络DenseNet每一块训练的特征信息来自于前面网络的所有块,保留了更多特征。而从实验结果来看,除偏航角外,9层简单卷积神经网络的结果均明显优于其他卷积神经网络的测量结果。分析认为,作为特征标识物的黑白棋盘格的特征较少且容易提取。较之于ResNet和Dense Net等深层网络来说,浅层网络更易于拟合。同时浅层网络也没有过多信息特征冗余,所以精度更高,效果更好。从ResNet152的测量结果也可以印证这一点。相比于ResNet50和DenseNet,它基本处于未拟合的状态，输入范围为-0.5°～0.5°,偏航角的平均误差却高达1.7°,效果差于随意猜测一个值,可见网络未能成功描述此函数关系。同理,15层卷积神经网络增加了网络的复杂度,最终得到的特征图较小,损失了一些关键信息,导致检测精度下降。

总的来说,9层卷积神经网络已经可以较好地拟合出从输入图片到输出其位置和姿态的函数关系,无需复杂的多层网络。

为探究不同激活函数对位置和姿态参数估计的影响,本文选用了ReLU、tanh、ELU和sigmoid这4个常见的激活函数进行对比。激活函数不同时训练得出的位置和姿态的平均误差表如表3所示。(注：激活函数不同指的是除最后一层激活函数为Linear不变之外其余全部均做替换)

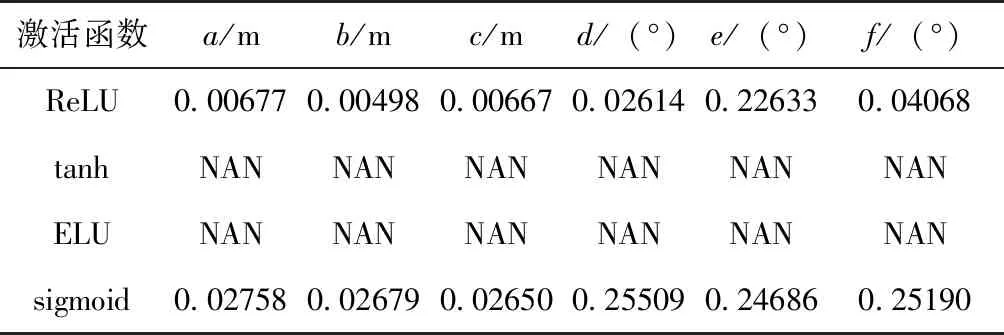
表3 不同激活函数的六维度平均误差

从实验结果来看,ReLU作为激活函数时网络精度较好,显著优于收敛速度较慢的sigmoid函数。而另外两个常用的激活函数直接导致网络不收敛。分析认为,激活函数ReLU负半轴均为0的性质增强了网络整体的非线性表达,同时ReLU函数仅需简单的判定,这极大地加快了训练网络的速度,达到了最优。而sigmoid激活函数和均方差损失函数的组合使梯度下降较慢,同时网络训练速度慢,最终在训练轮数相同的情况下,sigmoid函数激活的网络并没有较好的拟合,精度较差。所以,最终本文选择了ReLU作为激活函数。

为探究学习速率对位置和姿态参数测量的影响,本文选取0.03、0.04、0.05这3个学习速率进行探究。学习速率不同时训练得出的位置的平均误差表如表4所示,姿态的平均误差表如表5所示。

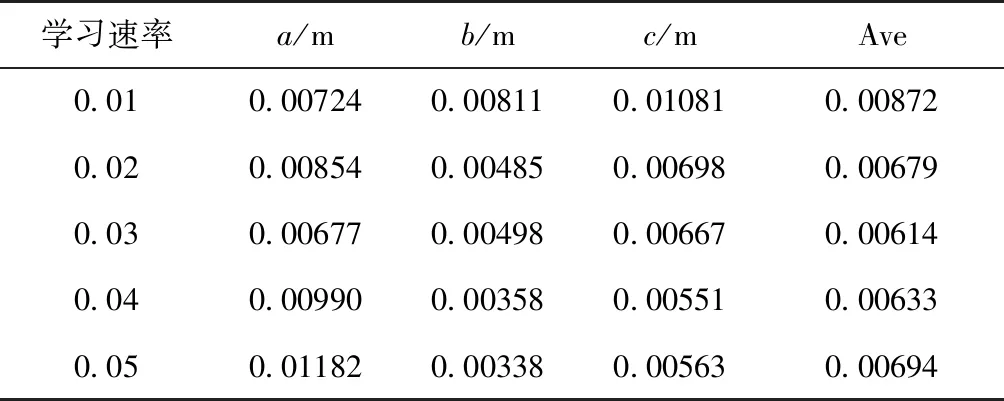
表4 不同学习速率的位置平均误差

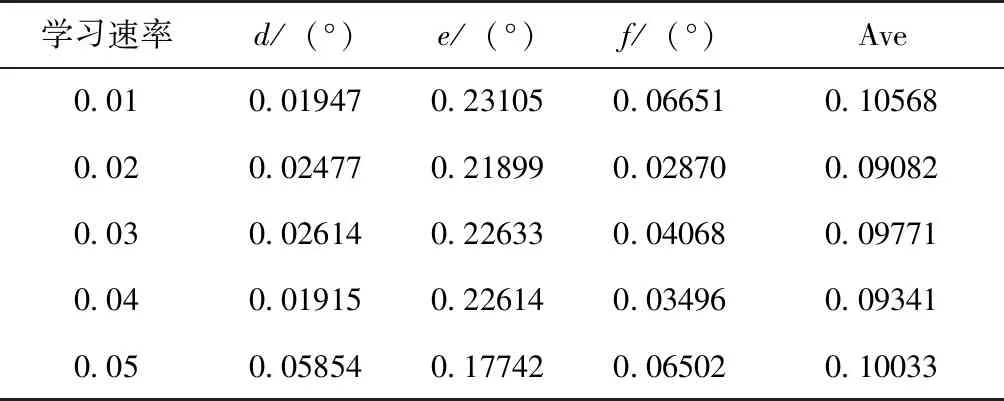
表5 不同学习速率的姿态平均误差

从实验结果来看,在位置平均误差方面,对于x方向来说,学习速率为0.03时网络精度最高；对于y方向来说,学习速率为0.05时最好；对于z方向来说是0.04时最好。同理,在姿态平均误差方面,也出现了这样分布的特点。分析认为,对于摄像机来说,各位置、姿态并不等价,虽然在图片输入时特征标识物为正方形,y和z方向的表现理应相同,偏航角和滚转角的表现理应相同。但图像输入时经过了从原始图像到512*256的统一变换,使位置、姿态6个维度方向上的表现具有各自的特点。所以不同的学习速率在各位置和姿态的表现并不相同。通过计算平均数发现,学习速率为0.03～0.04较为合适,略优于学习率为其他时的情况。位置的单位是m,姿态的单位是(°),两者没有直接的可比性。若位置精度要求为1cm时,位置已达到精度要求,此时应选学习速率为0.04。

为探究输入图像大小对位置和姿态参数估计的影响,本文选取了512×256、480×480、640×640这3个典型尺寸进行探究,其中640×640即为原图像大小。输入图像大小即代表着每一张图片向卷积神经网络中输入信息量的多少。512×256=131072,480×480=230400,从包含的像素点来看,后者图像中包含的信息量大约为前者的1.75倍。而640×640的图像中包含的信息量大约是480×480中的1.77倍。输入网络中的图像大小不同时训练得出的位置的平均误差表如表6所示,姿态的平均误差表如表7所示。

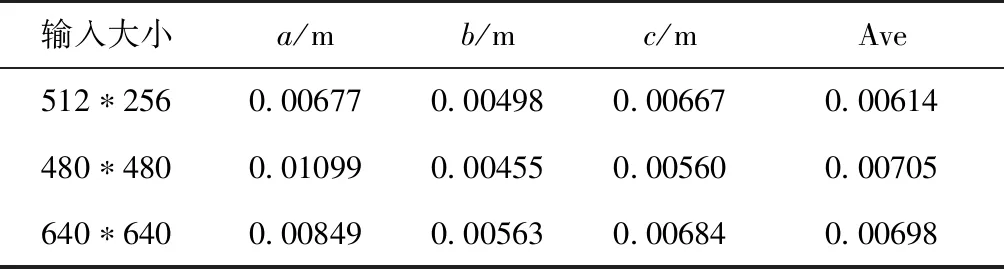
表6 不同图像输入大小的位置平均误差

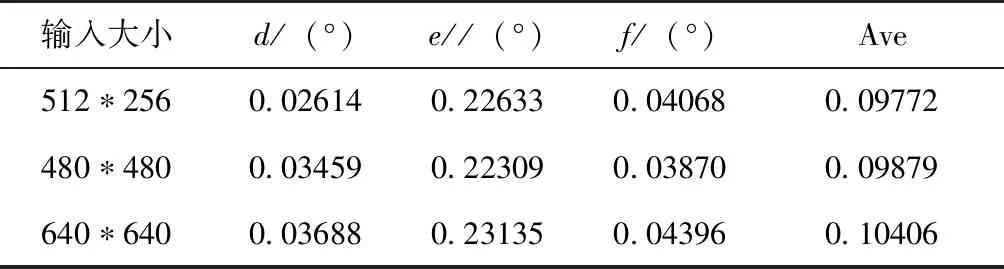
表7 不同图像输入大小的姿态平均误差

从实验结果来看,输入图像大小为512×256时对于x方向和俯仰角的训练效果最好,且明显优于其他两种情况。而在剩下4个维度的训练中,除了z方向上明显低于输入图像为480×480的精度,其余均无明显差距。而输入图像为640×640时全方位的精度均有所下降。分析认为,输入图像过大会导致图像特征冗余,反而不利于神经网络的训练。而经过512×256变换的图像在y方向和z方向信息不均等,反而在旋转时为网络提供了更鲜明的信息,最终效果佳。最终选择将图像变换大小为512×256。

3 结论

1)本文实现了利用卷积神经网络对带有标识物的航天器6个维度姿态的测量,通过仿真实验结果可知,态势分析系统可以较为精确地测量6个维度的位姿。

2)对于姿态估计问题,通过仿真实验结果证明简单的9层卷积神经网络能更好地对航天器姿态进行估计。

3)在学习速率合适的情况下,ReLU作为激活函数可以给网络增加更多的非线性特征,能够对姿态估计的非线性函数进行较好的拟合。