一种步进式压电陶瓷驱动器负载模型研究

王学亮 彭吉 徐立松 李朋志 陈雪 郑楠 李佩玥

摘  要： 为了能够准确高效地以步进式压电陶瓷驱动器进行定位控制，文中对其在不同负载力条件下的位移性能进行了研究。首先，设计和实施了测定驱动器位移?负载力曲线的实验;然后，通过高阶多项式拟合的方法对实验结果进行拟合，分析得到可用的拟合结果，将其作为被测驱动器的位移?负载力关系;最后，随机选取了其他的负载力条件，将实测位移量与通过拟合曲线进行计算的结果进行对比，验证该位移?负载力模型的准确性。实验结果表明，使用该方法获得的步进式压电陶瓷驱动器的位移?负载力模型可用2阶多项式关系进行描述，与实测值的误差约为1%，可为后续针对该驱动器进行定位控制算法设计提供支撑。

关键词： 压电陶瓷; 步进式驱动器; 定位控制; 负载实验; 多项式拟合; 数据分析

中图分类号： TN305.7?34                           文献标识码： A                      文章编号： 1004?373X（2020）02?0014?03

Study on a load model for stepping piezoceramic actuator

WANG Xueliang1，2，3， PENG Ji1，2，3， XU Lisong1，2，3， LI Pengzhi1，2，3， CHEN Xue1，2，3， ZHENG Nan2，3， LI Peiyue2，3

Abstract： The displacement performance of the stepping piezoceramic actuator under different load force conditions isstudied to accurately and efficiently perform the positioning control with it. The experiment of measuring the displacement?load force curve of the actuator was designed and implemented. The experimental results are fitted by means of the high?order polynomial fitting method， and the available fitting results are obtained by analyzing， which are taken as the displacement?load force relationship of the actuator under test. Other load force conditions are selected randomly， and the measured displacement values are compared with the results calculated by the fitted curve to verify the accuracy of the displacement?load force model. The experimental results show that the displacement?load force model of the stepping piezoceramic actuator obtained with this method can be described by the second?order polynomial relation， and the error of this method is about 1% in comparison with the measured value; which can provide a support for the subsequent design of positioning control algorithm for this actuator.

Keywords： piezoceramic; stepping actuator; positioning control; load experiment; polynomial fitting; data analysis

0  引  言

壓电陶瓷材料具有分辨率高、频率特性好、输出力大、无磁干扰和发热小等优点，被广泛作为纳米级定位系统的执行机构使用[1?4]。叠堆式压电陶瓷的伸长量通常为陶瓷自身长度的0.1%，因此很难使用叠堆式压电陶瓷实现mm量级的定位行程[5?7]。为了实现mm量级的定位行程，同时保证nm量级的定位精度，人们利用多个叠堆式压电陶瓷构建了步进式压电陶瓷驱动器，具有体积小、行程大和精度高等优点。国内外的学者对步进式压电陶瓷驱动器开展了广泛的研究：黄卫清等人针对光波导封装应用场景，研究了一种非共振式压电电机驱动的旋转定位平台，通过连续作动和步进作动两种工作模式实现大行程和高精度[8];HO和JAN提出一种具有交流?直流复合驱动模式的步进式压电电机，通过交流驱动模式和支流驱动模式的切换，既可以实现高速运动又可以实现nm量级分辨率[9];曹小涛等人为实现大行程和高精度的位移控制，利用非共振式尺蠖型压电直线电机，基于高压功率运算放大器，设计了非共振式压电直线电机的精密复合放大驱动电路和具有迟滞前馈的复合控制算法[10];DENG和XU等人提出一种基于压电材料的二维弯曲特性制成压电步进驱动器[11]，针对该类驱动器，通过施加双相支流驱动电压，提出了八步运动规划[12];程光明等人针对压电惯性驱动器，研究了压电双晶片振子在方波激励下的冲击响应，使用加速度传感器测试惯性冲击力，完成实验验证[13]。

以上的研究多针对步进式压电陶瓷驱动器的构建和驱动等问题展开，而针对其定位性能受外部负载力影响，即位移?负载力模型的研究较少。而在实际使用步进式压电陶瓷驱动器构建定位系统时，为了保证nm量级的定位精度，通常使用柔性结构作为压电陶瓷驱动器的导向，当输出位移量时，随着压电陶瓷驱动器的推动，柔性结构发生形变，对驱动器施加的外部负载力随之变化，这将导致驱动器的控制模型发生改变。虽然这种影响可以通过外部加入位移传感器构成位置闭环系统最终加以消除，但将不可避免地增加算法的迭代次数，进而影响定位系统的快速性。为了准确高效地使用步进式压电陶瓷驱动器进行高精度的快速的定位控制，本文对步进式压电陶瓷驱动器的位移?负载力模型进行研究。

1  研究对象及其工作原理

本文的研究对象为Physik Instrumente（PI）公司N?111.20型压电陶瓷驱动器，该驱动器采用一种称为NEXLINE的步进技术实现：驱动器内部由运动轴和压电叠堆组成。其中压电叠堆分为两组，每组由剪切（shear）叠堆组件和夹持（clamp）叠堆组件构成，共计4种压电叠堆组件，分别为clamp1组件、shear1组件、clamp2组件和shear2组件。当N?111.20型压电陶瓷驱动器工作时，4种压电叠堆组件按特定时序运动如图1所示。clamp组件交替夹紧运动轴，期间shear组件交替产生位移，如此往复。利用这种多个压电叠堆的时序运动，N?111.20型驱动器可以实现大行程下的高精度定位。

当外部负载力发生变化时，由于压电陶瓷材料本身的特性所限，在相同的驱动电压下压电叠堆产生的位移也将随之改变。图2示意了一种标称位移30 μm@1 000 V，刚度为200 N/μm的压电叠堆的位移?负载力曲线，可以看到随着负载力逐渐变大，在相同驱动电压下压电叠堆所产生的位移量逐渐减小。步进式压电陶瓷驱动器是由压电叠堆组件所构成，因此不可避免地其输出位移也受到外部负载力影响，但同时由于其内部复杂的工作原理，其位移?负载力的关系也更加复杂。

2  设计实验

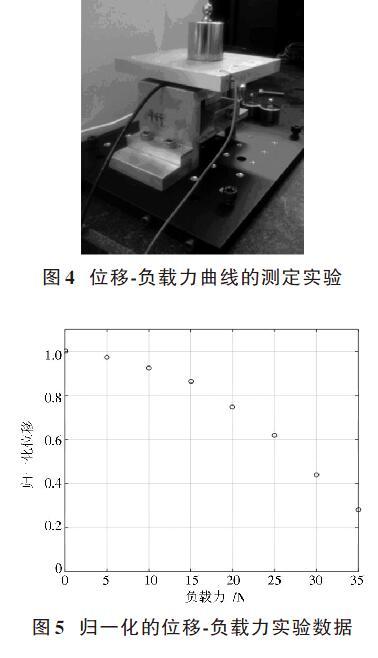
为了获得N?111.20型步进式压电陶瓷驱动器的位移?负载力关系，本文设计了如图3所示的实验装置。驱动器被夹紧工装固定于底部隔震平台，并由夹紧工装保证其运动轴垂直于隔震平台，运动轴上固定托架工装，通过向托架工装上增减砝码来调整驱动器所受外部负载力。另有一Z形支撑工装，其上固定电容传感器，并以托架工装下表面为被测面，以此检测驱动器的位移量。

实验过程如图4所示。首先保持驱动器空载，对驱动器施加步进信号，同时通过电容传感器测量和记录其位移增量。然后控制驱动器返回原工作起点，重复两次上述过程，以三次位移测量值的平均值作为当前负载力条件下的位移测量结果。以500 g为增量逐步向托架工装上安装砝码，并重复上述过程，获得不同负载力条件下的位移值。

通过上述实验方法，对N?111.20型步进式压电陶瓷驱动器的位移?负载力曲线进行测量，并且对位移数据进行归一化处理，得到位移?负载力数据点如图5所示。可以看到该驱动器随着外部负载力的增加，其输出位移量逐渐减小，且曲线具有非线性特征。

3  数据分析

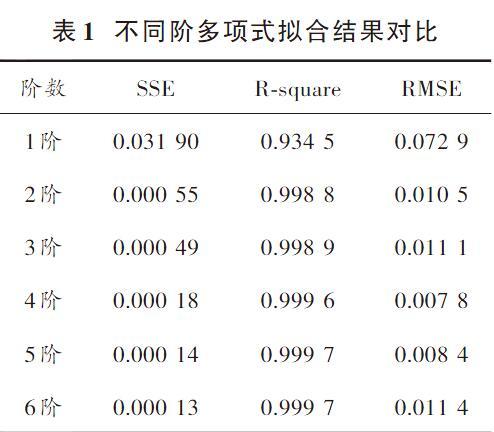
本文对以上实验数据进行了多阶多项式拟合，拟合结果如表1所示。可以看到，除了采用1阶多项式拟合以外获得结果都具有较小的和方差（SSE）与标准差（RMSE），同时其确定系数（R?square）>99%，都是可用的拟合结果。同时，综合考虑驱动器使用过程中其控制算法的复杂性和实时性，最终选定2阶多项式拟合的结果，并获得N?111.20型压电陶瓷驱动的位移?负载力的关系为：

[df=-0.000 55f2-0.001 7f+0.999 2]

式中：d是归一化处理后的位移;f是单位为牛顿的负载力。

为了验证拟合结果的准确性，随机选取了3组负载力，测试了驱动器对应条件下的位移，并对比拟合曲线的计算结果，如表2所示。可以看到，通过拟合曲線计算的结果与实际测量的结果相差不大，误差约为1%，因此，拟合曲线的结果是基本准确的。

4  结  论

本文针对步进式压电陶瓷驱动器在不同负载力条件的位移性能进行了研究，提出一种位移?负载力曲线的测量方法，并使用该方法对N?111.20型步进式压电陶瓷驱动器进行测试。对实验结果进行拟合分析得到N?111.20型压电陶瓷驱动的位移?负载力之间的2阶多项式关系。验证结果表明，通过该拟合曲线计算的结果和实际测量的结果误差约为1%，能够为后续针对该驱动器进行定位控制算法设计提供有效支撑。

参考文献

[1] 郭嘉亮，李朋志，李佩玥.压电陶瓷定位系统电容传感器容错控制[J].现代电子技术，2014，37（21）：152?155.

[2] PAN Qiaosheng， ZHANG Qi， WANG Hongbo， et al. Piezoelectric linear motor using resonant?type clamping based on harmonic vibration synthesis [J]. Mechatronics， 2014， 24： 1112?1119.

[3] 王学亮，李佩玥，郑楠，等.运放对压电陶瓷驱动电路系统精度影响的研究[J].电子测量技术，2014，37（10）：33?36.

[4] 安凯.压电驱动器电压及其频率对驱动速度的影响[J].现代电子技术，2014，37（13）：113?115.

[5] SUN Xiantao， CHEN Weihai， ZHANG Jianbin， et al. A novel piezo?driven linear?rotary inchworm actuator [J]. Sensors and actuators A： physical， 2015， 224： 78?86.

[6] 于月民，冷劲松.新型压电旋转驱动器的设计与性能测试[J].机械工程学报，2015，51（8）：185?190.

[7] 韩丽玲，潘成亮，鲁思颖，等.新颖微型压电旋转关节的建模与仿真[J].纳米技术与精密工程，2016，14（3）：229?236.

[8] 黄卫清，陶杰，孙梦馨，等.非共振型压电电机驱动的大行程精密定位旋转平台的建模和实验[J].光学精密工程，2016，24（11）：2712?2720.

[9] HO Shinetzong， JAN Shanjay. A piezoelectric motor for precision positioning applications [J]. Precision engineering， 2016， 43： 285?293.

[10] 曹小涛，李德全，李洪文，等.非共振式压电直线电机精密驱动及定位控制[J].光学精密工程，2017，25（8）：2139?2148.

[11] DENG Jie， LIU Yingxiang， CHEN Weishan， et al. Development and experiment evaluation of an inertial piezoelectric actuator using bending?bending hybrid modes [J]. Sensors and actuators A： physical， 2018， 275： 11?18.

[12] XU Dongmei， LIU Yingxiang， LIU Junkao， et al. Motion planning of a stepping?wriggle type piezoelectric actuator operating in bending modes [J]. IEEE access， 2016， 4： 2371?2378.

[13] 程光明，李曉旭，温建明，等.压电惯性驱动器惯性冲击力的分析与检测[J].光学精密工程，2015，23（6）：1681?1687.

作者简介：王学亮（1984—），男，辽宁铁岭人，硕士，主要研究方向为精密位移控制系统设计。