沙地樟子松边材液流速率的方位差异特征
党宏忠 冯金超 韩 辉
(1.中国林业科学研究院荒漠化研究所 北京 100091; 2. 辽宁省沙地治理与利用研究所 阜新 123000)

由于方位差异的普遍存在,单单从某一方位测定的边材液流速率用于估算单株液流时可能并不可靠,而实践中仅通过加大探头数量(如每株树安装多达6个以上探头(López-Bernaletal., 2010)的方法,不仅会大幅度增加观测成本,而且对于胸径较小的树木,会引起相邻加热探针的相互干扰而导致测定结果异常(赵平等, 2005)。Js方位差异尽管具有不对称性,且在不同个体间存在不确定性(Fernándezetal., 2001; Oliverasetal., 2001),但各方位间一般具有高相关性(马玲等, 2005; 王华等, 2010; Luetal., 2000)。因此,就某一树种而言,用较少的方位测定来推算整树液流速率的可靠模型与方法,这对于提高单株液流的估算精度、节俭观测成本具有十分重要的意义(Komatsuetal., 2016)。
樟子松(Pinussylvestrisvar.mongolica)是我国三北防护林建设中最重要的树种之一。在我国,樟子松的天然分布主要集中于大兴安岭南侧红花尔基一带(焦树仁, 2001)。自20世纪50年代以来,樟子松被引种到科尔沁沙地建设防风固沙林(焦树仁, 1986; 朱教君等, 2003),并自此陆续在整个北方地区引种推广,对我国的“三北”防护林建设具有重要作用。然而随着林龄的增加,以及全球气候变化的影响,樟子松林分普遍产生了早期的生长衰退甚至死亡的现象,林分密度与水资源供应间关系的失衡被普遍认为是引起林分衰退的主要原因或诱因(移小勇等, 2006; 朱教君等, 2005),而精准估算单株乃至林分的蒸腾用水量对于揭示樟子松的衰退原因有重要作用。鉴于此,本研究对沙地樟子松Js方位间的差异做出科学的评价,并提出整株树平均液流速率估算的简化模型,旨在探寻兼顾估算精度与节约成本的对单株蒸腾估算的方法。
1 材料与方法
1.1 研究区概况
试验地选择在辽宁省固沙造林研究所实验林场三家子工区。该实验林场位于科尔沁沙地东南缘,地理位置42°40′57″ N,122°33′06″ E,海拔207 m,年均气温6.3 ℃,全年无霜期150~160天,年均降水量475.5 mm(1954—2010年),60%~70%集中在6—8月,年蒸发量1 553.2 mm,约为降水量的3.27倍。该区土壤以风沙土为主,沙土颗粒均匀,沙层厚度126~128 m,沙层的颜色和机械粒径成层更迭分布,变化比较明显,沙土瘠薄,有机质含量较低,一般为0.3~0.99 g·kg-1。林下灌木主要有: 鸡桑(Morusaustralis)、榆树(Ulmuspumila)幼苗(盖度<1%)、胡枝子(Rhamnusdavurica)(盖度<1%)等; 草本主要为马唐(Digitariasanguinalis)(盖度约47%)、拂子茅(Calamagrostisepigeos)(盖度约16%)、碱草(Aneurolepidiumchinense)(盖度约15%)、中华隐子草(Cleistogeneschinensis)(盖度约10%)等18种草本(总盖度约93%)(韩辉等, 2015)。
1.2 研究方法
1.2.1 降水及土壤水分监测 降水通过在试验林分外50 m处的空旷地上架设的小型气象站观测,雨量桶传感器来自于美国AVALON公司。数采器为SQ2020(英国Grant公司)。采样间隔为10 min,记录间隔为30 min。在样地内株间随机选择3处监测土壤水分动态。每处均在距表层0.1、0.2、0.4、0.6、0.8和1 m处分别安装ECH2O土壤水分传感器(Decagon Devices Inc., USA),连接Em50数据采集器,采集间隔为30 min。传感器监测数据通过在试验地用烘干法校正的经验方程计算出土壤体积含水率(θ,%)。
土壤水分相对有效指数(REW)的计算采用公式(Granier, 1987; Orenetal., 1999):
(1)

1.2.2 树干边材液流速率的监测 在沙地樟子松成熟林内建立20 m×20 m的试验样地。选择4株生长健康的樟子松大树开展液流速率的监测。样树基本情况见表1。液流速率的测定采用Granier式热扩散传感器(TDP-3 cm,澳大利亚Dynamax 公司)测定。该传感器由上下2根探针组成,其中上部探针为加热探针。每个样树分别在东、南、西、北4个垂直方位(根据手持罗盘仪确定)各安装1套TDP-3 cm传感器,所有传感器连接16通道SQ2020数采器(英国Grant公司)。数据采集间隔为10 min,记录间隔为30 min。采用100 W多晶太阳能板接12V-100AH铅酸蓄电瓶连续供电。TDP安装过程及技术要点见文献(Dangetal., 2014; 党宏忠等, 2010)。边材液流速率(Js,cm·h-1)的计算采用Granier(1987)公式:
(2)
式中,ΔT为上下两探针间实际温差(℃), ΔT0为液流为零时上下两探针间的温差(最大值,℃),该值以10天为1个周期采用两次回归法确定(Granier, 1987; Luetal., 2004)。
边材宽度采用生长锥钻取树芯(试验结束后),并通过颜色变化确定边材与心材边界。

表1 样树基本情况Tab.1 Information of sample trees for measuring sap flow density
1.2.3 数据处理及分析 为消除样树个体间差异并便于比较,每株样树以在整个观测期内测得的最大液流速率值为参考值进行标准化处理,称为相对液流速率(Js/max,无量纲)。北、西、南、东4个方位的相对液流速率分别记为Js/max-N,Js/max-W,Js/max-S与Js/max-E。4个方位Js/max的平均值作为整个样树的液流速率(Js/max-mean)。不同方位间相对液流速率的比较采用单因素方差分析方法(One-way ANOVA)在统计软件OriginPro2018中完成,其中多重比较采用Tukey HSDposthoc在α=0.05或0.01为显著性临界水平进行判断。
除了采用调整决定系数(Adj.R2)外,还利用统计量评估方程拟合或模型的优度和精度Cai等(2007):
均方根误差(RMSE):
(3)
平均误差(ME):
(4)
符合指数(d):
(5)
式中,当d值接近于1时表示对观测值的最佳预估。

在OriginPro2018(OriginLan Inc., Northampton, MA, USA)中做图。
2 结果与分析
2.1 主要环境因子的季节动态
2016年4月1日—10月31日为樟子松主要生长季。试验期间共观测到20次有效降雨事件(> 10 mm·d-1),总计降雨量为600.8 mm,为典型的湿润年份。但降水具有明显的季节分异特征,在生长季的前半期,降水只占整个生长季降水的33%,而后半期降水占比高达67%。与此同时,前半期1 m内平均REW为0.38(θ平均为8%),明显低于后半期的0.63(θ平均为11.9%)。尤其是在前半期有61天的REW低于0.4(θ< 8.4%)而处于干旱状况,其中REW最低值仅为0.16(θ=4.8%, 2016-07-17),土壤水分处于严重亏缺状态。整个生长季期间,1 m内土壤水分状况对强降雨事件的响应比较敏感(图1)。

图1 生长季降水量、土壤水分相对有效指数(REW)的动态变化Fig.1 Dynamic changes in daily precipitation and soil moisture relative effective index (REW) during the growing seasonREW=0.4 (Granier,1987)作为阈值来划分土壤干旱与湿润状态。 The thresholds value of REW = 0.4 (Granier, 1987) was used to classify soil drought and wetting.
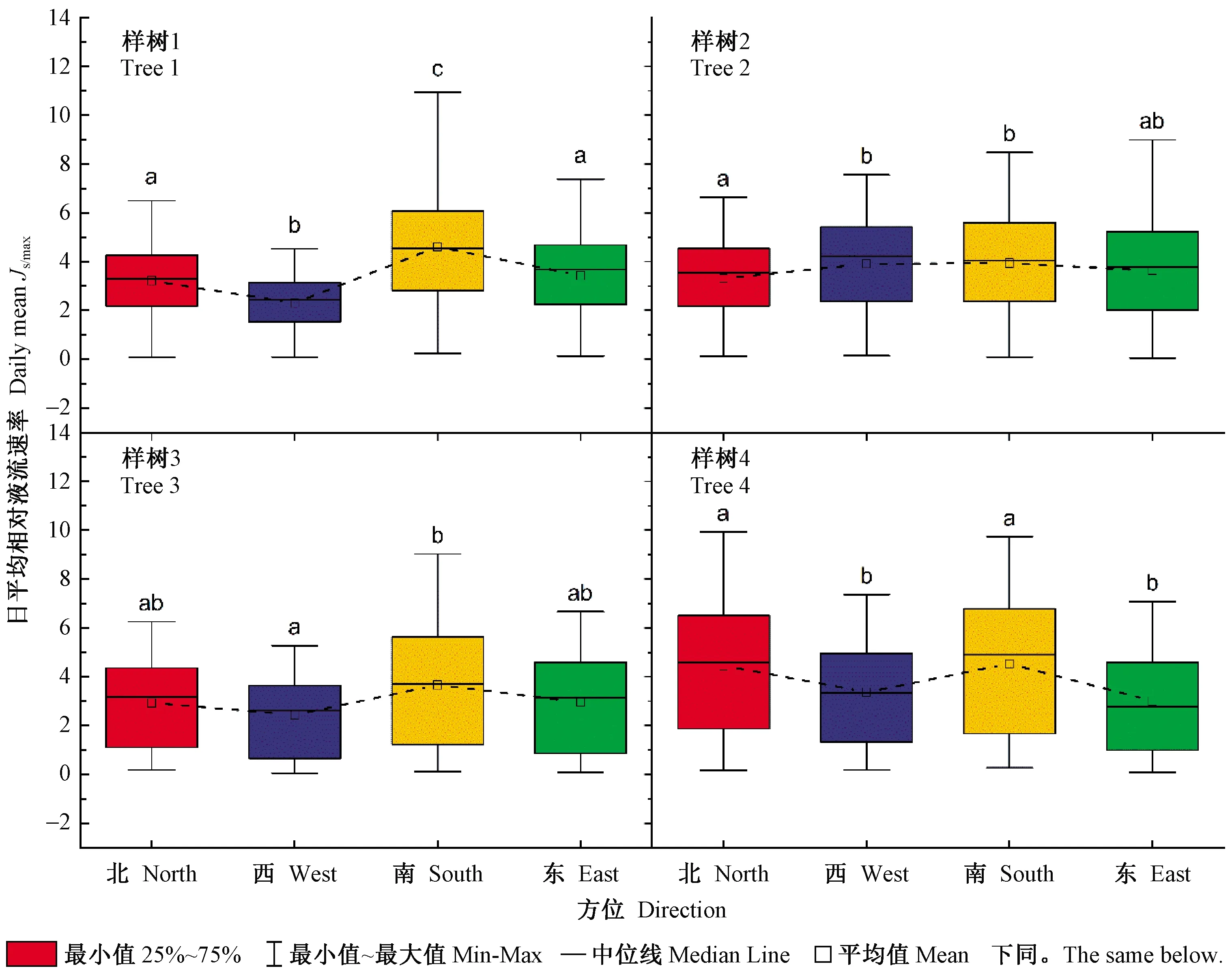
图2 生长季不同方位相对液流速(Js/max)日平均值的比较Fig.2 Comparison of daily mean values of relative sap flux density, hourly sap flux density divided by the maximum in the whole study period (Js/max), in different azimuthal direction during the growing season不同字母代表差异显著性。Different letters represent the difference in significance.
2.2 不同方位液流速率的差异
对4株样树不同方位日平均相对液流速率(Js/max)的比较表明,不同方位的Js/max不仅有着明显的不同,而且还存在着个体差异(图2)。对于样树1,最高的日均液流速率值来自于南侧(Js/max-S为4.6),其次为东侧(Js/max-E为3.4)和北侧(Js/max-N为3.2),西侧最低(Js/max-W为2.3),南侧液流速率与其他方位的存在显著差异(P<0.01)。对于样树2、样树3和样树4,最高液流速率同样均来自于南侧,Js/max-S值分别为3.9、3.7和4.5,但最低液流速率的方位在不同样树间不一致,分别来自于北侧(Js/max-N为3.3)、西侧(Js/max-W为2.4)和东侧(Js/max-E为3.0),不同样株的各方位Js/max值的差异程度不同。
2.3 土壤干旱对不同方位液流速率的影响
在生长季的前半期,尽管大气蒸发需求较后半期强劲,但降水相对少且土壤含水率较低,试验区樟子松遭遇了极端干旱的胁迫。方差分析结果表明,在干旱期(REW< 0.4),Js/max-N日平均为(0.11 ± 0.007),显著低于湿润期(REW ≥ 0.4)的(0.16 ± 0.006)(P< 0.001)。类似地,Js/max-W在干旱和湿润期的值分别为(0.10 ± 0.007)和(0.14 ± 0.006),Js/max-S分别为(0.15 ± 0.01)和(0.20 ± 0.009),Js/max-E分别为(0.11 ± 0.008)和(0.15 ± 0.007),除西侧的液流速率在干旱期与湿润期具有显著差异外(P=0.017),其他方位均呈极显著差异(P< 0.01)(图3)。

图3 湿润和干旱土壤不同方位相对液流速率(Js/max)差异性比较Fig.3 Comparison of standardized sap flux density(Js/max)at different azimuthal directions in wet soil moisture condition with that in drought soil moisture condition
2.4 不同方位液流速率间的关系
为了明确不同方位间液流速率间的定量关系,本研究以北侧(通常选择在树干北侧测量,减少阳光直射带来的测量误差)为因变量,建立其他方位与Js/max-N间的回归关系。结果表明: 各方位液流速率与北侧液流速率均有紧密的线性相关(Adj.R2> 0.93,P<0.01),但不同个体间相关紧密度存在差异。如对于西侧与北侧间的线性相关,相关紧密度(直线斜率)在0.7~1.2,样树2和样树3更接近于1(图4a)。对于南侧与北侧间的线性相关,相关紧密度(直线斜率)在1.06~1.39,样树4更接近于1(图4b)。对于东侧与北侧间的线性相关,相关紧密度(直线斜率)在0.79~1.10,样树3更接近于1(图4c)。
2.5 估算整树平均相对液流速率的简化模型及可靠性检验
为明确不同方位液流速率对于整株树液流速率(Js/max-mean,4个方位的平均值)的代表性,简化野外测定的工作量,笔者对整个生长季的数据集按单双日划分为相等数量的2个样本,样本1用于拟合各方位相对液流速率与Js/max-mean间的线性关系。样本2用于模型精度的检验。结果表明: 北侧相对液流速率(Js/max-N)与平均液流速率(Js/max-mean)间的线性相关更紧密(Adj.R2> 0.99,P<0.01,RMSE=5.47)(图5a),斜率为1.015,接近于1,表明用北侧液流速率的测定能够更好的代表对整株树的平均液流速率,据此建立用北侧液流速率估算整株平均液流速率的简化模型。
Js/max-mean=1.015×Js/max-N。
(6)
进一步利用样本2对该模型进行验证,通过对观测计算的Js/max-mean与模型预估值(利用北侧液流速率观测值通过模型推算)的比较,结果表明: 该模型对4株样树(独立样本)均取得了精度均高的估算(d=0.99, RMSE < 0.05)(图6)。

图4 生长季北侧液流速率(Js/max-N)与其他三侧相对液流速率间相关性间的相关性Fig.4 The standardized sap flux density in the north-side (Js/max-N) related to the other sides 西侧(Js/max-W)、南侧(Js/max-S)和东侧(Js/max-E)West-side (Js/max-W), South-side (Js/max-S), and East-side (Js/max-E).
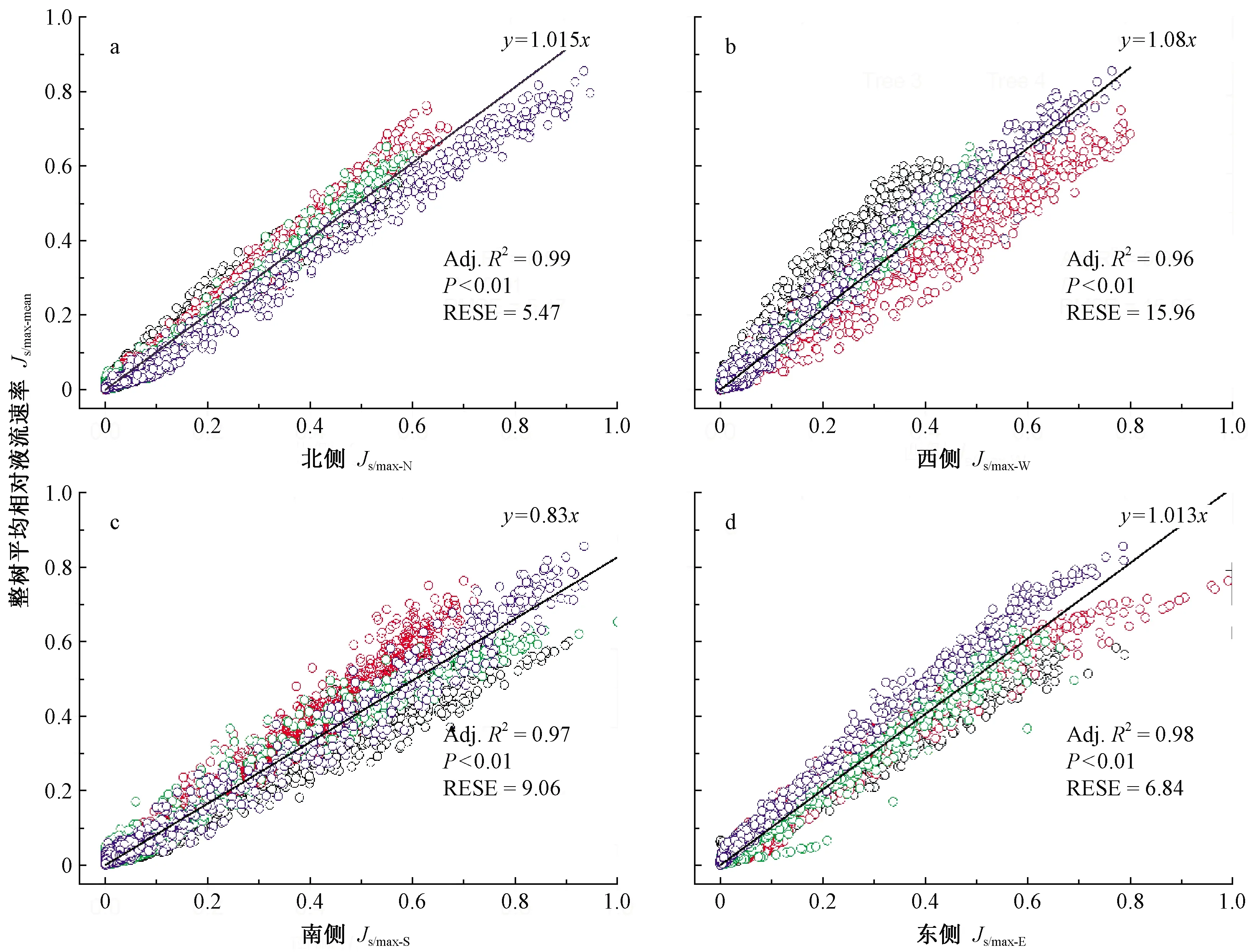
图5 生长季4个方位相对液流速率(Js/max)与整树相对液流速率平均值(Js/max-mean)间的相关性Fig.5 Relationship between the standardized sap flux density in each side (Js/max) and the mean standardized sap flux density during the whole growing season (Js/max-mean)

图6 整树液流平均速率的预估值与测定值间的关系Fig.6 The relationship between the predicated value and the measured value for standardized sap flux density (Js/max-eam)
3 讨论
许多树种的树干液流在不同方位存在着显著的差异,如马占相思(Acaciamangium)(马玲, 2005)、芒果(Mangiferaindica)(Luetal., 2000)、侧柏(王华田, 2006)等,而关于不同树种液流速率方位差异的规律,目前并不明确。如黄土区果树南侧液流速率最大,北侧最小,东、西侧较为接近(孟秦倩等, 2013)。黄土丘陵区枣树表现为西向液流速率较高(马建鹏, 2016),胡杨表现为东、西侧液流速率最大(司建华, 2004),而沙柳(Salixcheilophila)和小叶杨的方位差异关系不固定,并且随季节而变化(徐丹丹, 2017)。本研究中监测到樟子松南侧液流速率较高,但各方位间的相对大小顺序存在个体间的差异(图2),方位差异在同一个体上比较稳定但在不同样木上顺序并不一致的现象在元宝枫(Acertruncatum)等树种上也有报道(王瑞辉等, 2006)。
关于树木个体边材液流速率方位差异的原因与机制,有研究认为与树木冠层对阳光的曝露程度的不同有关(Granier, 1987; Orenetal., 1999; Shinoharaetal., 2013);也有研究认为可能是由于不同方位的木质部生长速度的分化带来管腔直径(vessel lumen diameter)大小的不同,导致水力导度的差异(Tateishietal., 2008)以及导管系统发达程度的分化或枝下高的不同(王华, 2010)所致;也可能与根系的不均匀分布(异质生境)有关(Nadezhdina, 2010)。树冠结构引起的冠层接受光照时间及光合有效辐射量的不同进而引起液流的方位差异也被认为是主要原因(López-Bernaletal., 2010)(梅婷婷等, 2012),但是也有报道认为被测木树干不同方位边材宽度、相应方位的冠幅大小与液流速率大小的关系并不明确(王华田, 2006)。从本研究中南侧液流速率普遍较高(图2),结合对北方地区油松(Pinustabulaeformis)等树种相似的测定结果来看(王华, 2010),北半球南侧受光较多可能是主要原因之一。
松属(Pinus)等针叶树种一般具有通直、均一的树干和近似于圆锥体的树冠,相对于阔叶树种而言,边材的宽度在不同方位间一般具有较好的一致性。本研究中笔者发现了樟子松不同方位间液流速率的显著差异(图2,图3),且方位差异格局在不同个体间还存在着不确定性,这表明考虑不同方位液流速率差异的必要性。为了解决方位差异对单株液流通量估算可能带来的误差,在实际研究中,一个可行的方案是根据不同树种边材液流方位变异程度和树干直径,适当增加探头的数量,如有学者认为DBH < 15 cm的单株可用1个探头,15~20 cm的用2个探头, 20 cm以上的用3~4个(Granier, 1987)甚至6个以上探头(López-Bernaletal., 2010),但过多探头必须大幅度增加观测成本,且带来严重的干扰与误差(赵平, 2005)。尽管樟子松液流速率的方位差异较大,但同一个体不同方位的液流速率间呈紧密的线性相关(Adj.R2∶0.93~0.99,P< 0.01,图4),这与许多树种的测定结果一致(马玲, 2005; 王华, 2010; Luetal., 2000),因此只需测定某一方位的液流速率后经模型估算整树平均液流速率,并进一步估算林段的蒸腾成为可能(赵平, 2005)。本研究北侧液流速率比其他方位液流速率能更好地代表樟子松整树的平均液流速率,且斜率接近于1(图5a),这表明对于该区域的樟子松而言,利用北侧液流速率通过简化模型能够实现较高精度地估算整树平均液流速率(图6)。本研究结果对于降低野外测定成本,提高单株蒸腾量估算精度提供了重要依据。
4 结论
对樟子松大树4个垂直方位液流速率整个生长季的监测结果表明: 樟子松树干液流速率存在显著的方位差异,一般南侧液流速率相对较高,但各方位间的相对大小顺序存在着个体间差异。土壤水分亏缺均显著引起各方位液流速率的同步下降。树干北侧方位的液流速率与其他方位间均具有紧密的线性关系。模拟结果表明,作为液流测定中较常采用的方法,从北侧测定的液流速率能较好地代表樟子松整株树平均液流速率,对建立的模型经独立样本的检验,精度达到0.99以上。

