带电粒子在匀强磁场中做圆周运动的圆心确定方法

(甘肃省华亭市第二中学，甘肃 华亭 744100)

1 引言

带电粒子在匀强磁场中运动的问题是高中物理教学的重点，也是难点，更是历年高考的热点。解决带电粒子在磁场中运动问题的基本思路是：先分析粒子的运动过程，确定运动轨迹的圆心，画出轨迹圆；再综合运用洛伦兹力、向心力及圆的几何知识进行求解。这类问题对学生的综合能力要求较高，多数学生感到困难，无从下手。其主要原因是学生不能在圆周运动与圆之间建立联系，也就不能根据圆的几何关系找到圆心，不能画出圆弧，也就不能顺利解决问题，可见确定圆心是解决这类问题的突破口。

2 典型例题分类解析

2.1 已知粒子射入、射出磁场的速度方向

例1：如图1所示，一个质量为m、电荷量为q(q<0)的带电粒子从x轴上的P(a，0)点以速度v，沿与x轴正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限，不计粒子重力。求：(1) 匀强磁场的磁感应强度B和射出点的坐标；(2) 带电粒子在磁场中的运动时间。

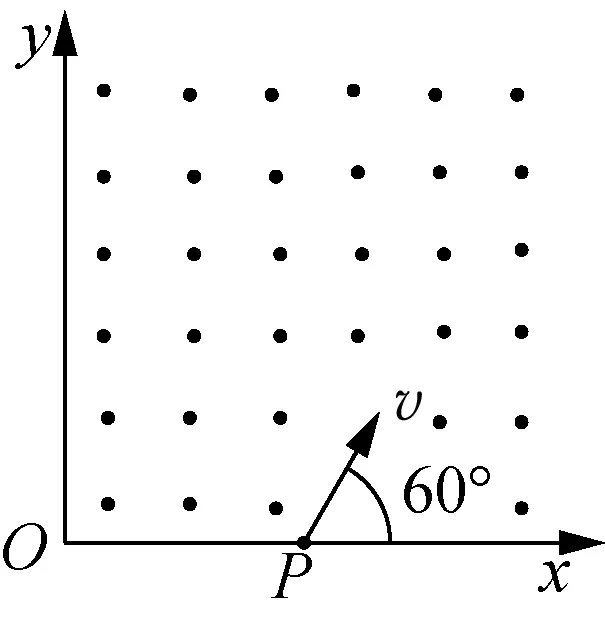
图1

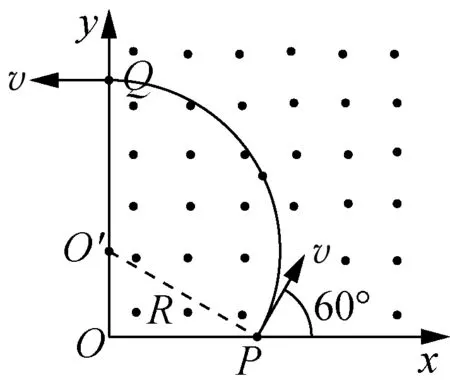
图2

解析：已知电荷射入和射出磁场的方向，根据速度方向与圆半径的垂直关系，可知y轴是圆的一条直径，再过P点做速度的垂线，这条垂线就是另一条直径，两条直径的交点就是圆心。

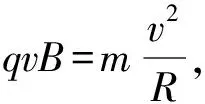
2.2 已知粒子射入磁场的速度方向和射入磁场、射出磁场的位置

例2(2016年四川卷)：如图3所示，正六边形abcdef区域内有垂直于纸面的匀强磁场。一带正电的粒子从f点沿fd方向射入磁场区域，当速度大小为vb时，从b点离开磁场，在磁场中运动的时间为tb，当速度大小为vc时，从c点离开磁场，在磁场中运动的时间为tc，不计粒子重力,则( )。

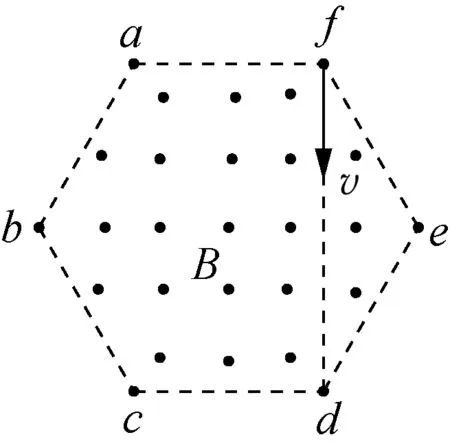
图3

A.vb∶vc=1∶2，tb∶tc=2∶1

B.vb∶vc=2∶1，tb∶tc=1∶2

C.vb∶vc=2∶1，tb∶tc=2∶1

D.vb∶vc=1∶2，tb∶tc=1∶2

解析：已知粒子射入磁场的速度方向和射入、射出磁场的位置，两位置的连线是圆的弦，弦的中垂线过圆的一条直径，速度的垂线过圆的另一条直径，两直径的交点就是圆心。

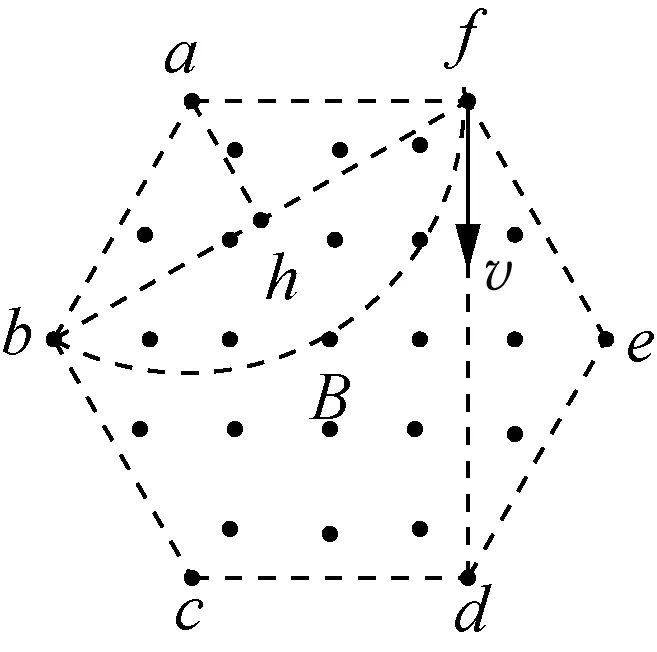
图4

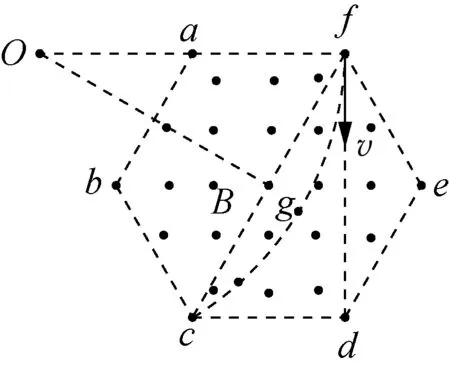
图5

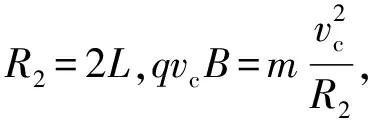
图4和图5中圆弧所对应的圆心角分别为120°和60°，根据粒子做圆周运动的时间与圆心角成正比，则有：tb∶tc=2∶1，故选项A正确。

2.3 已知粒子射入磁场的速度方向和任一速度的方向

例3(2016年新课标Ⅲ卷)：平面OM和平面ON之间的夹角为30°，其横截面(纸面)如图6所示，平面OM上方存在匀强磁场，磁感应强度大小为B，方向垂直于纸面向外。一带电粒子的质量为m，电荷量为q(q>0)。粒子沿纸面以大小为v的速度从OM的某点向左上方射入磁场，速度与OM成30°角。已知粒子在磁场中的运动轨迹与ON只有一个交点，并从OM上另一点射出磁场，不计重力。粒子离开磁场的射点到两平面交线O的距离为( )。

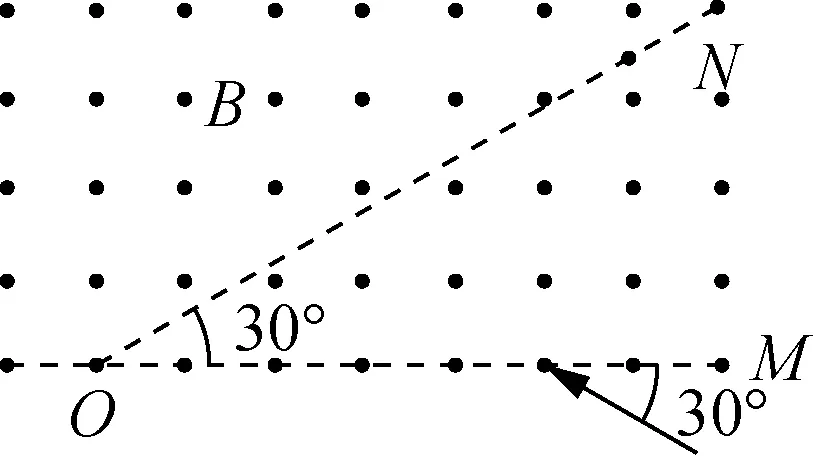
图6

解析：已知粒子射入磁场时的速度方向和圆轨迹的一条切线，根据速度方向沿着切线方向，可画出两切线的夹角，该夹角的平分线经过圆的一条直径。再画出入射速度的垂线可得到另一条直径，两条直径的交点就是圆心。

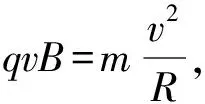
图7

2.4 已知粒子射入磁场的速度方向和射出磁场时速度方向的偏向角

例4(2013年新课标Ⅰ卷)：如图8所示，半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面)，磁感应强度大小为B，方向垂直于纸面向外。一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为R/2。已知粒子射出去的磁场与射入磁场时运动方向间的夹角为60°，不计重力，则粒子的速率为( )。

解析：已知粒子射入磁场时的速度方向和射出磁场时的偏向角，由偏向角与轨迹圆的圆心角相等，可知弦与半径的夹角为60°、弦和两半径构成等边三角形。

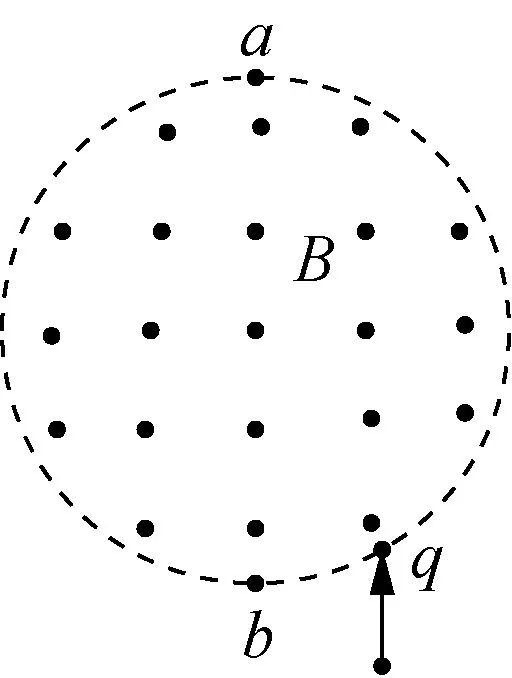
图8

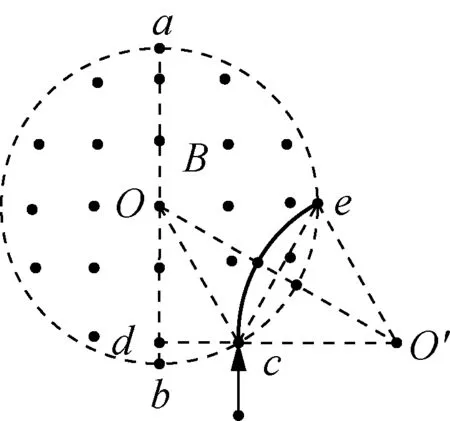
图9

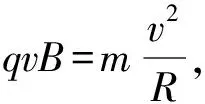
3 圆心的确定方法

根据“圆与圆周运动”的关系及4道典型例题的分析求解，总结确定圆心的方法如下：

(1) 若知道粒子射入磁场和射出磁场时的速度，分别作出两速度的垂线，则两垂线的交点就是圆心；

(2) 若知道粒子射入磁场的速度和射出磁场的位置，连结粒子射入与射出磁场的两位置得到圆弧的弦，再画出弦的中垂线和射入磁场的速度的垂线，则两条垂线的交点就是圆心；

(3) 若知道粒子射入磁场的速度和粒子做圆周运动的圆弧的一条切线，画出速度的延长线，该速度的延长线是圆弧的另一条切线，再作两切线相交的夹角的平分线和速度的垂线，则角平分线与速度的垂线的交点就是圆心；

(4) 若知道粒子射入磁场的速度和射出磁场时速度的偏向角，根据速度的偏向角与圆心角相等的关系可得到弦与半径的夹角，就可以画出弦，再作出速度的垂线和弦的中垂线，则两垂线的交点就是圆心。

4 教学建议

带电粒子在匀强磁场中的圆周运动问题与几何密切相关，是物理与数学相结合的一类综合问题，对学生应用数学解决物理问题的能力要求较高，而学生的困难之处恰是不能将圆的几何知识迁移到圆周运动中来，没能抓住它们之间的内在联系。针对这一现象结合实际教学，给出以下3点教学建议。

(1) 复习初中数学中圆的相关知识，让学生熟悉切线、直径、圆心角、弦的几何关系，为圆周运动的学习做好准备。

(2) 引导学生建立圆与圆周运动之间的相互联系，突出数学知识在物理问题中的应用。

(3) 鼓励学生多作图，培养学生使用尺规作图的习惯和作图、识图的能力，在作图的过程中体会“找圆心”的基本方法。