无机支柱真空玻璃的封接边缘受力分析

刘敏孙诗兵吕锋李要辉王晋珍

(1.北京工业大学 材料科学与工程学院， 北京100124；2.中国建筑材料科学研究总院， 北京100024)

0 引言

真空玻璃是一种热损失极小而可见光透过率较高的新型玻璃。 两片平板玻璃之间由按一定顺序排列的支撑柱隔开，边缘处由封接焊料封接，在某一块平板玻璃的一角处设置抽真空的排气口，将腔体中的空气抽完后密封得到真空玻璃。

使用无机支撑柱代替金属支撑柱，可以有效改善真空玻璃传热系数不理想和支撑柱与平板玻璃接触界面处的支撑柱失效的问题。 目前真空玻璃生产中使用较多的是金属支撑柱，关于真空玻璃的受力、传热数值模拟分析[1-8]都是用弹性模量较高(约为210 GPa)的不锈钢或合金支撑柱，几乎没有对使用无机支撑柱的真空玻璃的受力分析。

真空玻璃的封接焊料是国内外学者研究的重点和热点，有学者利用有限元软件对低温封接材料[7，9-11]和工艺[12-15]进行研究，但很少有封接边缘部分受力的研究。 许海凤等[16]提出封接玻璃焊料受拉力、封接玻璃界面受拉力和剪切应力是引起真空玻璃边缘破损的原因，并且采用十字交叉法对玻璃焊料进行3 点弯曲强度实验，测试各种荷载下封接焊料的拉伸粘结强度，证明目前的封接技术满足强度要求。 由于真空玻璃受力时边缘部位的情况复杂，影响到靠近边缘位置支撑柱的受力，理论计算需要大量工作，且得到的结果并不一定准确。 利用有限元软件对真空玻璃在各种荷载下进行模拟，分析其受力，可以得到详细直观的结果，更好地为真空玻璃的发展提供依据。

文章利用ANSYS 有限元软件对无机支撑柱的真空玻璃进行模拟受力分析，主要研究封接边缘的受力情况及其对真空玻璃受力的影响。

1 无机支柱真空玻璃有限元模型的建立

真空玻璃中平板玻璃的厚度远小于边长，可以看作薄板，选用SHELL 单元。 支撑柱为圆柱形，直径为0.5～1 mm、高度为0.15～0.25 mm，体积相对玻璃板非常小，采用LINK 单元。 其实体模型为1 条长度为支撑柱高度的直线，设置其面积参数为支撑柱上下底面的面积大小。 封边采用SOLID 和SHELL 单元建模都不能得到理想结果，所以将其简化成紧密排布的LINK 单元，封边LINK 单元的截面面积总和为封接面积。 在实体模型的基础上划分网格得到真空玻璃有限元模型。

建立了300 mm×300 mm 的真空玻璃模型，如图1 所示。 计算在大气压下真空玻璃的受力和变形情况，分析封接边缘区域如何受力。 真空玻璃的规格参数为:平板玻璃弹性模量为70 GPa、支撑柱和封接边缘的弹性模量为75 GPa、平板玻璃厚度为5 mm、支撑柱半径和高度都为0.2 mm。 网格大小为1 mm，分别计算了封边宽度为10(5 排间隔2 mm 的LINK 单元)、8(4 排间隔2 mm 的LINK 单元)、6 mm(3 排间隔2 mm 的LINK 单元)时，真空玻璃的变形和受力情况。 约束和荷载如下:

(1) 将有限元模型中所有重合的节点在Z方向耦合，即将封边和支撑柱粘结在玻璃板上；

(2) 所有耦合的节点Ux、Uy为0，即封边和支柱与玻璃板接触的部分位移一致；

(3) 封边和支撑柱的底面，即所有LINK 单元另一端的节点Uz为0；

(4) 在玻璃板上施加100 000 Pa/m2，即1 个大气压大小的均布荷载。

在以上有限元模型的基础上进行计算和后处理，得到无机支柱的真空玻璃中平板玻璃在大气压下的受力情况。 真空玻璃中平板玻璃在大气压下会发生弯曲变形，产生位移，利用ANSYS 中的坐标轴建立模型时，平板玻璃的厚度方向为z轴，大气压力的方向与z轴负方向一致，平板玻璃在厚度方向发生的位移如果与大气压力方向一致则为正，反之为负。

图1 300 mm×300 mm 真空玻璃模型图

2 封接边缘受力分析

2.1 封边宽度的影响

建立边长为300 mm，封边宽度分别为10(5 排间隔2 mm 的LINK 单元)、8(4 排间隔2 mm 的LINK 单元)、6 mm(3 排间隔2 mm 的LINK 单元)，网格大小为1 mm 的真空玻璃模型，计算出1 个大气压下真空玻璃的变形和受力大小，计算结果见表1。 以封边宽度10 mm 为例，其位移和应力分布云图如图2 所示。 由表1 可以看出，当封边宽度增加时，平板玻璃的最大位移变小，而平板玻璃受到的最大压应力增大。 由位移和应力分布图可以看出，由于封边的影响，真空玻璃最靠近封边的一圈支撑柱在大气压下的变形和受到的压应力比其他支撑柱小，而第2 圈支撑柱的变形和受到的压应力最大。

数据分析模型如图3 所示。 图3(a)中红色框内表示真空玻璃上方的5 排封边处的LINK 单元，由上到下为上封边1～5 排LINK 单元。 绿色框中表示真空玻璃左边的5 排封边处的LINK 单元，由左到右为左封边1～5 排LINK 单元。 根据真空玻璃结构的对称性，下封边和上封边一致，右封边和左封边一致，所以不再作分析。 将封边区域的LINK 单元分为8 部分，如图3(b)所示。 图3(c)中的1 ～5 代表从下到上的5 排支撑柱，同样根据结构对称性，上面4 排支撑柱与下面4 排一致。

表1 封边宽度不同时真空玻璃的受力情况表

图2 封边宽度10 mm 计算云图

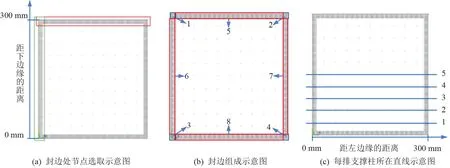
图3 数据分析模型图

在有限元计算中，每1 个节点都对应1 个位移，根据真空玻璃结构对称性，选择左侧封边5 排LINK单元节点和由下往上前5 排支撑柱进行分析。 将节点的位移作图，可以得到真空玻璃封边及平板玻璃的受力情况。 边长为300 mm、封边宽度为10 mm，即5 排LINK 单元；封边宽度为8 mm，即4 排LINK单元；封边宽度为6 mm，即3 排LINK 单元的位移变化图如图4 所示。 LINK 单元的位移出现波浪状与模型有关，将封边简化成排列的LINK 单元，在LINK 单元与平板玻璃接触的节点处位移比较小，在分析时应忽略波浪形状，取平均值。 由图4 可以看出，真空玻璃的封边区域的位移有正有负，受压为正、受拉为负，封边即受压力，也受拉力，且拉力由封边区域的平板玻璃和封接焊料共同承受。 在大气压的作用下，300 mm×300 mm 的真空玻璃承受的压力为9 000 N。 当封边宽度为10 mm 时，封边处上、下、左、右由LINK 单元组成，每个角即图3(b)中的1～4部分为重合部分，分别为25 个LINK 单元。 封接边缘部分的LINK 单元承受的力为2 384.06 N(正负抵消后)，81 个支撑柱承受的力为6 615.88 N，两者共同承受8 999.94 N 的压力，与实际情况符合。

通过对比发现，在3 种不同封边宽度的真空玻璃计算中，距离平板玻璃边缘最远的一排LINK 单元的位移全为正方向，而其他几排LINK 单元的位移变化趋势为由正变负，如当封边宽度为10 mm时，靠近平板玻璃左边缘最近的一排LINK 单元的位移，在距下边缘25 mm 处开始由正变负，距下边缘275 mm 处开始由负变正，封边处位移变化具有对称性。 由此可得真空玻璃的受力示意图，如图5所示。 除封接边缘区域矩形框内部分受拉力外，其他部分在大气压的作用下都受压力。

将封边宽度分别为6、8、10 mm 的真空玻璃左封边第1 列(离边缘最近)LINK 单元和第5 列(离边缘最远)LINK 单元的位移分别进行比较，发现封边宽度越小，封边处节点位移绝对值越大，即封边承受的力越大，如图6 所示。

图4 左边封边区域LINK 单元节点位移图

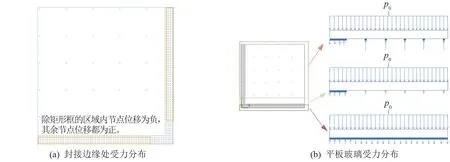
图5 真空玻璃受力分布图

图6 不同封边宽度下最靠近与最远离边缘的第1 列LINK 节点位移图

真空玻璃中由下往上5 排支撑柱所在直线所有节点的位移如图7 所示。 平板玻璃在封边处的位移为2～3 μm，其数值很小，目前没有能够测试此数量级应变的仪器，所以实验结果有待进一步验证。 平板玻璃上与支撑柱接触位置的节点位移如图8 所示。 第1 排支撑柱位移最小，原因是第1 排支撑柱距离封边比较近，在边缘位置，封接焊料承担了大部分应力，而第2 排支撑柱的位移最大，第3、4、5 排支撑柱的位移比第2 排小，且大小接近。 可以看出，封边对第1 排和第2 排的支撑柱影响最大，离封边越远的地方受其影响越小。 由图8(a)可以得出，封边宽度越小，第1 排支撑柱的变形越大。

图7 平板玻璃上支撑柱所在直线的结点位移图

图8 平板玻璃上与支撑柱接触处节点位移图

根据第2 圈支撑柱受到的应力最大的结果，将封边宽度为10 mm 的真空玻璃第2 圈支撑柱的弹性模量增大至210 GPa，ANSYS 计算结果如图9 所示。 真空玻璃最大位移为2.26 μm，最大压应力为10.5 MPa。 与表1 中的结果相比，最大位移减小，最大应力增大。 所以在平板玻璃能够承受的应力范围内，将受最大应力的一圈支撑柱的弹性模量增大能起到优化结构的作用。

图9 第2 圈支撑柱增大后真空玻璃的位移和应力图

2.2 封接焊料弹性模量的影响

当真空玻璃间隙为0.3 mm，即支撑柱高度为0.3 mm时，计算不同弹性模量的封边，即E封边对其受力的影响，计算结果见表2。E封边变化对平板玻璃上其他部分影响较小，最大位移和最大压应力的值不会发生变化。E封边约为100 GPa 时，封边处受到的最小压应力最小，当E封边增大或减小时，最小压应力会稍微增大。

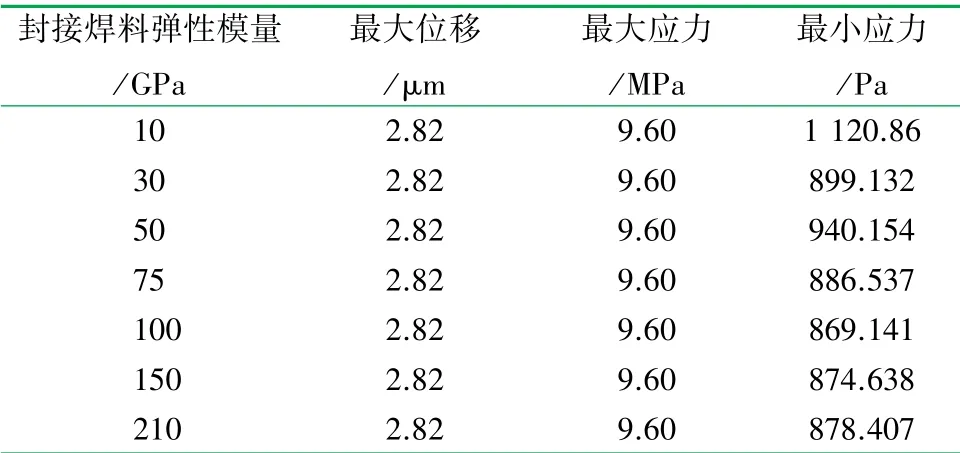
表2 封接焊料弹性模量不同时真空玻璃的受力情况表

最小压应力发生在真空玻璃角部，即真空玻璃的封边区域，所以将封边区域LINK 单元的节点位移作图进行分析，如图10 所示。 LINK 单元的节点位移(位移绝对值)随E封边的增大而减小，并且E封边＜50 GPa 时，其大小的变化对LINK 位移影响较大，E封边＞50GPa 时，随E封边增大，LINK 单元位移减小幅度会变小，且E封边越大，LINK 单元的位移越趋近于0。 图10(a)～(c)中显示靠近边缘的第1、2、3 列LINK 单元变形规律一致。 图10(d)中，E封边分别为10 和15 GPa 时，第4 列LINK 单元的节点位移全部为正，并且可以看出第4 列LINK 单元的节点位移从角部位置到中部的变化为先减小后增大再减小。第5 排LINK 单元的节点位移如图10(e)所示，与2.1中结果相同，位移全部为正，但E封边为15 GPa时，第5 排LINK 单元的节点位移最小。

2.3 支撑柱半径、高度的影响

表3、4 分别是当支撑柱半径和高度变化时，真空玻璃的位移和应力的大小。 由表3 可知，当支撑柱半径＜0.25 mm 时，真空玻璃在大气压作用下，随着半径的减小，受到的最大压应力会减小，最小压应力会增大，即最大压应力和最小压应力的差会随半径减小而减小，真空玻璃受力更均匀，但真空玻璃变形的最大位移会随半径减小而增大。 当支撑柱半径＞0.25 mm 时，真空玻璃受到的最大压应力没有发现明显变化，但是最小压应力会随着半径的增大而增大，最大位移会随半径增大而明显减小。 为了达到真空玻璃力学性能和热学性能平衡，在变形大小允许范围内，应该尽可能将支撑柱的半径减小。 由表4可知，平板玻璃的最大位移和角部的最小压应力随支撑柱高度的增大而增大，并且最大位移发生的位置会向平板玻璃中心方向靠近，最大应力随支撑柱高度增大而减小。 在变形允许的范围内，真空玻璃的支撑柱的高度可以适当增加。

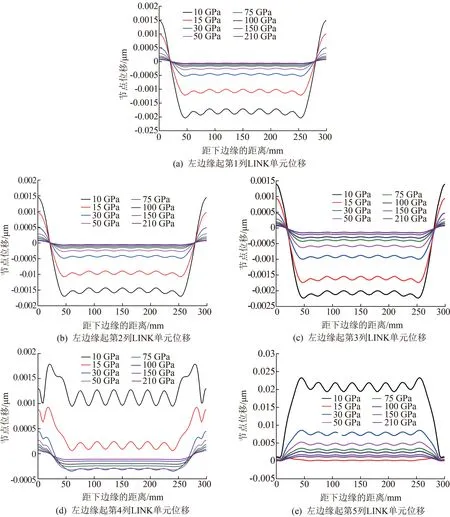
图10 不同弹性模量封边的真空玻璃封边区域位移比较图

表3 支撑柱半径不同时真空玻璃的受力情况表

3 结论

表4 支撑柱高度不同时真空玻璃的受力情况表

通过上述分析，得到以下结论:

(1) 在大气压作用下，真空玻璃的封边区域角部位置及最远离边缘的一部分封边受压，其他封边区域承受拉力，不与封边接触的部分全部承受压力。封边区域的受力会随封边宽度减小而增大。

(2) 真空玻璃的最大位移一般都发生在角部第1 排和第2 排支撑柱之间。 真空玻璃封边对第1 圈和第2 圈支撑柱的影响最大。 第1 圈支撑柱由于最靠近封边，其位移最小，即承担压力最小。 第2 圈支撑柱位移最大，从第2 圈开始，支撑柱处位移稍微减小，但远大于第1 圈支撑柱位移，越远离边缘受封边影响越小。

(3) 将位移最大的第2 圈支撑柱的弹性模量增大，甚至采用不同于无机支柱的刚性支柱，可以减小真空玻璃在大气压下的最大位移。

(4) 平板玻璃的最大位移和角部的最小压应力随支撑柱高度的增大而增大，并且最大位移发生的位置会向平板玻璃中心方向靠近。 最大应力随支撑柱高度增大而减小。 在变形允许的范围内，真空玻璃的支撑柱的高度可以适当增加。