压电陶瓷复合换能器固有频率的有限差分法∗

张 超 姚春东 具自强 贾贺通 董子龙 武 勇

0 引言

超声换能器是超声振动系统中最重要的部分之一[1]。在1880年居里兄弟发现压电效应以及1916年法国物理学家郎之万发明压电换能器之后[2]，压电陶瓷换能器因其机电转换效率高、成本低、容易成型等优势，已成为应用最为广泛的一种换能器。压电陶瓷复合超声换能器是近几年国内外专家学者的研究热点。事实上，压电陶瓷复合超声换能器的结构形式多种多样，例如：压电陶瓷圆管复合超声换能器(由压电陶瓷圆管与金属预应力管组成)、镶拼式复合压电超声换能器(由金属预应力管、可调柱形弹性胀套内芯和柱面压电陶瓷环组组成)、宽频带压电陶瓷换能器(由两个径向增强复合振子沿轴向叠加组成)等[3−5]。该类换能器的结构形式大多是在压电陶瓷圆环(管)与金属圆环(管)的复合结构上进行的进一步改进或集成。

为获得换能器的最佳工作状态，换能器的工作频率需为其固有频率，因此对换能器径向振动固有频率的计算就显得极为重要。考虑到换能器中压电陶瓷圆管与金属外圆管复合结构的典型性，本文以由径向极化的压电陶瓷圆管与金属预应力管沿径向复合而成的二元压电陶瓷复合换能器为例，利用有限差分法，通过对其固有频率的研究，以期说明有限差分法在计算压电陶瓷复合超声换能器固有频率方面的可行性及准确性。相关专家对上述结构换能器的固有频率进行了大量研究。例如：文献[6]基于薄壳理论，忽略了压电陶瓷薄圆管中的径向正应力及剪切力，分析了压电陶瓷薄圆管换能器的固有频率。文献[7]对由径向极化的压电陶瓷薄壁圆管和金属薄壁预应力管复合而成的换能器进行了固有频率的相关研究。文献[8]研究了由压电陶瓷薄壁圆管与金属预应力管所复合而成的换能器，对其固有频率进行了相关计算。文献[9]则研究了由径向极化的压电陶瓷圆管与金属预应力管沿径向复合而成的换能器，将其近似看成力学中的平面应变问题，分析了其纯粹的径向振动，得出了其等效电路及频率方程。针对上文中所指出的几种换能器的研究，都是基于本构方程、相容方程、波动方程，将换能器等效为等效电路图，从而推导出换能器径向振动的频率方程。这种方法可以对换能器径向振动的固有频率进行计算，但计算过程较为繁琐，且不易于计算机实现。

与之相比，有限差分法是求解变系数微分方程的有效手段，具有适用性强、逻辑清晰、计算机可编程程度高等显著优点[10]。利用有限差分法对换能器固有频率进行计算，可以大大缩短数学推导过程，公式复杂程度也会得以简化，还可进一步简化计算机编程过程。且有限差分法对换能器固有频率进行计算未见相关公开报道。基于以上考虑，本文提出计算换能器固有频率的有限差分法，希望能够丰富换能器固有频率的研究理论，以及提供一种新的计算方法供工程人员选择。本文推导了该换能器径向振动的数学模型及其有限差分形式，给出了对换能器径向振动固有频率理论计算的有限差分方法，并分析了换能器径向振动固有频率与其结构尺寸的影响关系。本文所建立的换能器径向振动固有频率的有限差分法具有一定的通用性，同样适用于结构形式相近的换能器及其他元器件。

1 换能器径向振动的有限差分形式

为便于研究，做如下假设：(1)换能器的轴向尺寸远大于其径向尺寸，按照弹性力学中的平面应变问题[11]，忽略其轴向振动，将其看作纯径向振动进行分析。(2)忽略压电陶瓷圆管与金属预应力管之间过盈量的影响。

图1为一个由内部径向极化的压电陶瓷圆管和外部金属预应力管复合而成的压电陶瓷复合超声换能器，图1(a)褐色部分为压电陶瓷圆管，空白部分为金属预应力管。ra、rb分别为压电陶瓷圆管内外径；rb、rc分别为金属预应力管内外径；h为换能器的高度；Er为外界激励电压。压电陶瓷圆管和外部金属预应力管为过盈配合。工作时，给予压电陶瓷圆管以外界电压激励，激发外部金属预应力管发生径向振动，从而沿径向产生声波辐射。

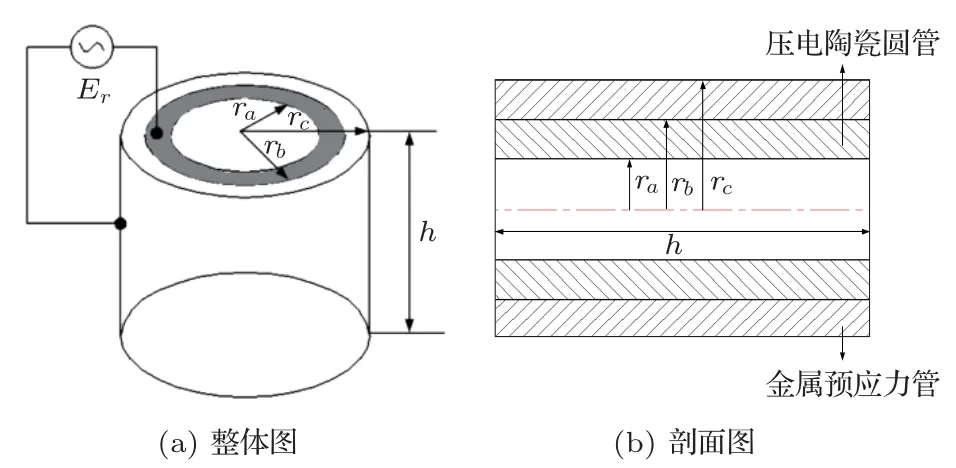
图1 换能器结构示意图Fig.1 Schematic diagram of the transducer structure

1.1 换能器径向振动的力学模型

由换能器的结构及工作原理，将换能器简化为由压电陶瓷圆管与金属预应力管组成的组合厚壁筒力学模型。图2为压电陶瓷复合超声换能器力学模型，Pe为换能器所受环境载荷。

图2 换能器径向振动的力学模型Fig.2 Mechanical model of radial vibration of transducer

1.2 换能器径向振动的数学模型

固有频率是物体的固有属性[12]，进行换能器固有频率计算时换能器应处于自由振动状态，此时没有外加电压激励和环境压力。针对1.1 节所建立的力学模型，综合压电弹性力学、厚壁筒理论可推导出换能器径向振动的数学模型为

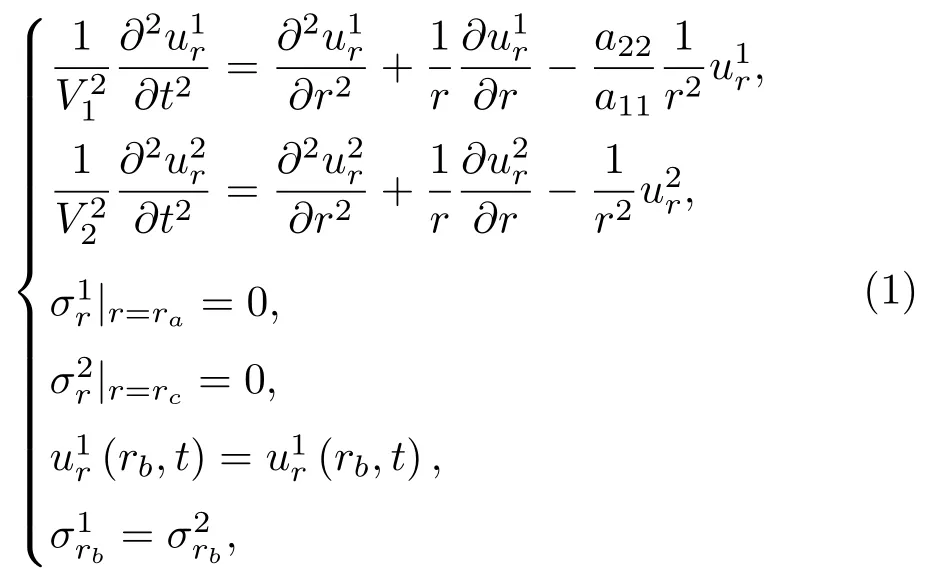
其中，

式中，u1r、u2r分别为压电陶瓷圆管、金属预应力管的径向位移；分别为声波在压电陶瓷材料、金属材料中的径向传播速度；ρ1、ρ2分别为压电陶瓷、金属材料的密度；σ1r、σ1θ、σ2r、σ2θ分别为压电陶瓷圆管、金属预应力管的径向、周向应力；SE11、SE12、SE13、SE33分别为压电陶瓷的弹性柔顺常数；E、γ分别为金属材料的杨氏模量和泊松比。

1.3 数学模型的有限差分形式

利用有限差分法进行计算，需先建立换能器径向振动的离散模型。取r-z平面为研究平面，沿径向将换能器进行离散为I个节点，单元长度为dr。压电陶瓷圆管内壁处为第一个节点，压电陶瓷圆管与金属预应力管配合处为节点i0，金属预应力管外壁处为节点I。图3为换能器径向振动的离散模型示意图。

对位移函数进行分离变量，有u1r=u1ejωt、u2r=u2ejωt，并由牛顿前差公式、中心差分公式，可得以下结论。

在压电陶瓷圆管内边界处， 0 边界条件σ1r|r=ra=0的差分形式为

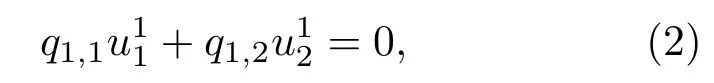
压电陶瓷圆管波动方程的差分形式为

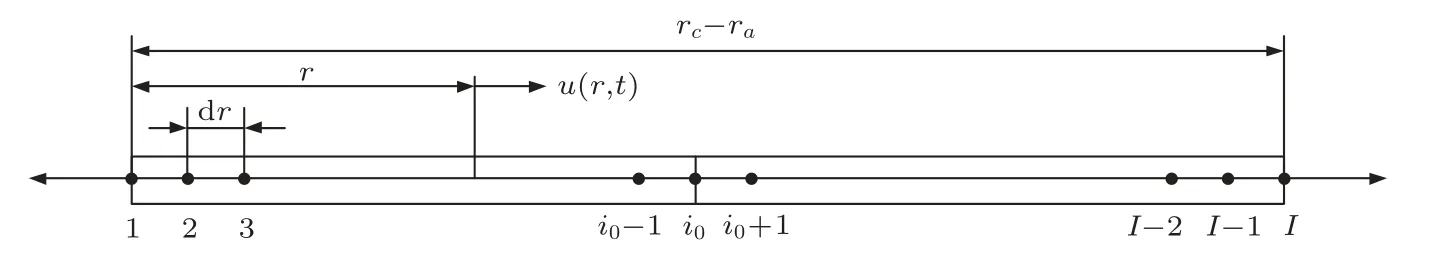
图3 换能器径向振动的离散模型Fig.3 Discrete model of radial vibration of transducer

其中，

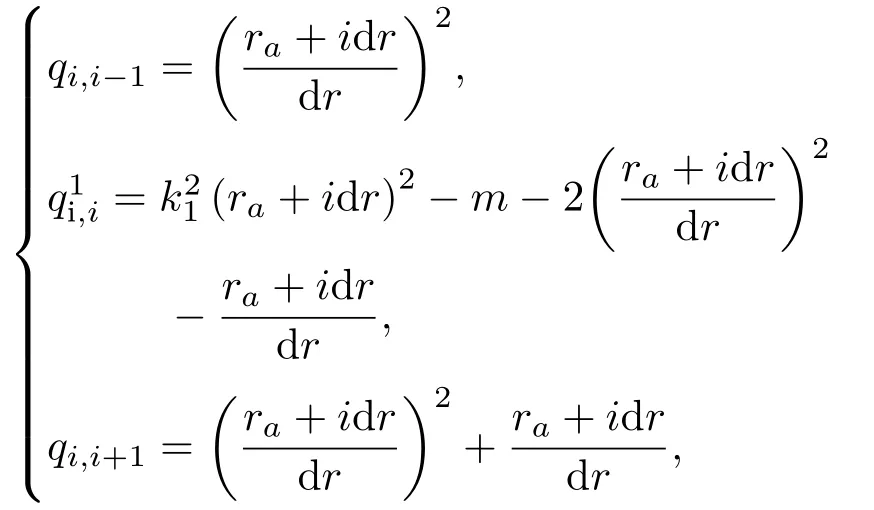
式中，k1=ω/V1为压电陶瓷圆管振子径向振动的波数；

压电陶瓷圆管与金属预应力管连续处，节点i0的差分形式为

其中，

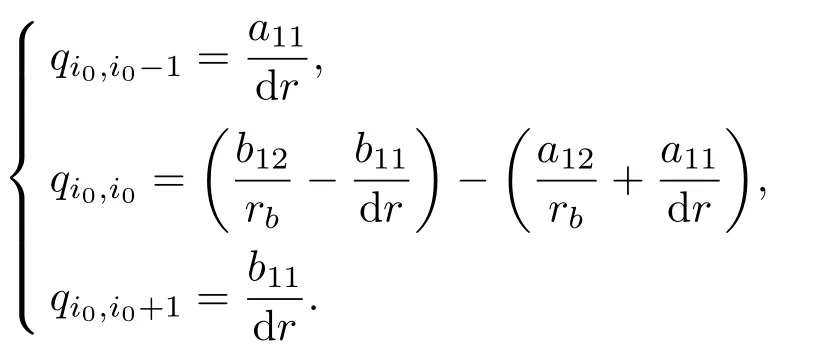
金属预应力管的波动方程的差分形式为

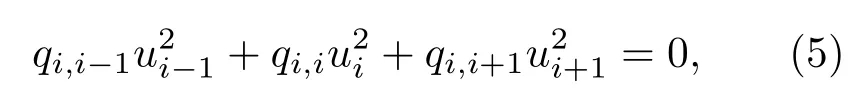
其中，

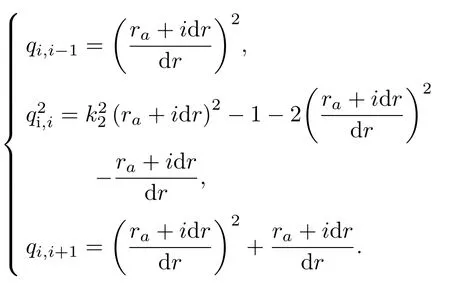
金属预应力管外壁边界处，边界条件σ2r|r=rc=0的差分形式为

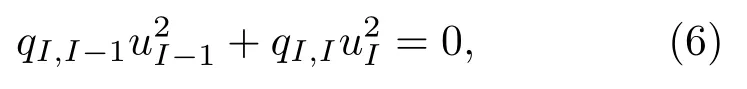
其中，

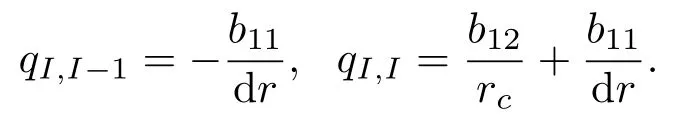
由以上结论，可以得到如下n阶齐次方程组：

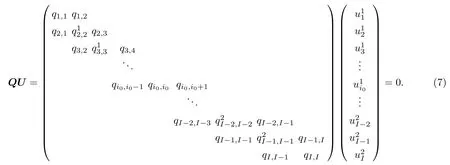
根据本文所建立的有限差分法，可以对式(2)～(6)进行变形处理为

式(8)中的第1 式和第5 式分别对应所建立力学模型的内外边界条件，在处理边界条件时，可以引入有限差分法进行边界处的节点进行数值计算；第2 式、第3式和第4 式可以对内部节点进行数值计算。当对时间同样进行离散处理时，并给定初始位移和初始速度时，可以根据所建立的有限差分法构建如图4所示的差分网格。

图4 差分网格Fig.4 Difference grid

图4中，矩形a 表示有限差分法进行计算时内边界处(第1 个节点)是如何进行数值计算的：首先假设内边界处节点位移为0；其次，根据初始条件计算出其他内部节点的位移；最后根据第2 个节点对内边界处节点位移进行覆盖计算。矩形b 表示有限差分法进行计算时外边界处(第I个节点)是如何进行数值计算的：首先，根据初始条件计算出其他内部节点的位移；最后根据第I-1个节点对外边界处节点位移进行计算。矩形c、矩形d 则表示内部节点的数值计算路线：某内部节点每一时刻的位移是由前一时刻的3 个节点位移及前二时刻的一个节点位移计算所得。

2 换能器径向振动的特征方程

式(7)为齐次线性方程组，其有非零解的条件是系数行列式为0，即：

矩阵Q为三对角矩阵，由高斯消元法对行列式|Q|进行处理，可得

其中，

方程(10)即为换能器径向振动的特征方程，求解方程(10)即可得换能器径向振动的n-1阶固有频率。

3 计算实例1

对压电材料为PZT-4 和金属预应力管为铝合金的换能器进行固有频率计算，以期验证有限差分法的可行性及准确性。其材料参数为：ρ1=7500 kg/m3，SE11=12.3×10−12m2/N，SE12=-4.05×10−12m2/N，SE13=-5.31×10−12m2/N，SE33= 1.55×10−12m2/N，ρ2= 2700 kg/m3，E= 7.15×1010N/m3，γ= 0.34。其结构参数为：ra= 21 mm，rb= 26 mm，rc= 31 mm，l1=l2=34 mm。

利用数值仿真软件进行编程，取不同的节点数以检验是否满足计算精度。节点数与固有频率关系曲线如图5所示。由图5可以看出，随着节点数的增加，固有频率也随之变大，直至接近某一固定值。针对该计算实例，可以看出，节点数从2001 个开始，固有频率变化非常缓慢，有限差分法达到一定的精度要求。为保证计算结果的准确性，取计算节点为2501 个，如表1所示，计算结果ft与文献[7]已有实验结果fe相差4.2%，符合很好，满足工程要求。

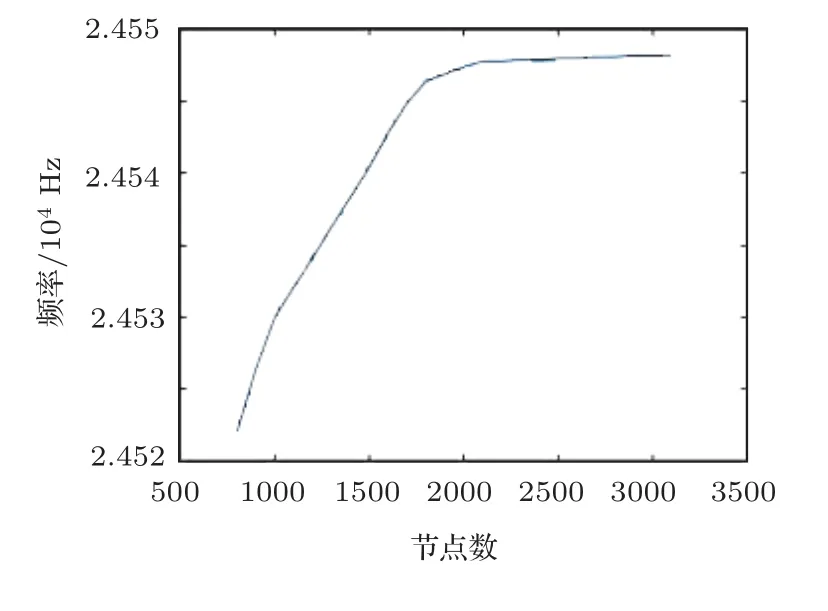
图5 频率与节点数关系曲线Fig.5 Relationship between frequency and number of nodes

表1 换能器固有频率的理论计算值及实验测量值Table 1 Theoretical calculation and experimental measurement of the natural frequency of the transducer

4 计算实例2

为进一步验证有限差分法的可行性及准确性，对与计算实例1 尺寸不同的换能器进行计算，其材料参数与计算实例1 完全一致，其结构参数为：ra= 50 mm，rb= 58 mm，rc= 63 mm，l1=l2=84 mm。

该计算实例固有频率与节点数的关系曲线如图6所示。由图6可以看出，固有频率在节点数为1951,之后变化非常缓慢，并随着节点数的增加，逐渐接近某一固定值。为保证计算精度，取节点为2601 个，如表2所示，计算结果ft与文献[7]已有实验结果fe相差1.85%，符合很好，满足工程要求。

图6 频率与节点数关系曲线Fig.6 Relationship between frequency and number of nodes

表2 换能器固有频率的理论计算值及实验测量值Table 2 Theoretical calculation and experimental measurement of the natural frequency of the transducer

5 换能器径向振动的固有频率与其结构尺寸的关系

针对不同结构尺寸的换能器，给出其径向振动固有频率与其结构尺寸之间的关系。换能器主要的结构尺寸为压电陶瓷圆管与金属预应力管的内外径，即ra、rb、rc。利用数值仿真软件进行编程计算，通过换能器径向振动特征方程得出不同结构尺寸下的换能器径向振动的固有频率。

保持压电陶瓷圆管与金属预应力管的壁厚不变，只改变压电陶瓷圆管的内径，即ra。取ra= 21～31 mm，压电陶瓷圆管与金属预应力管的壁厚为5 mm，计算结果如图7所示。由图7可以明显看出：换能器径向振动的固有频率随压电陶瓷圆管内径的增大而降低。

图7 固有频率与压电陶瓷圆管内径的关系Fig.7 Relationship between natural frequency and inner diameter of piezoelectric ceramic tube

保持换能器总壁厚不变，只改变压电陶瓷圆管与金属预应力管套装处尺寸rb，取ra= 21 mm、rc= 31 mm。引入壁厚比λ= (rb-ra)/(rc-ra)，壁厚比表示压电陶瓷圆管厚度占换能器总厚度的比例。当λ为0时，换能器就成为了一个金属预应力管；λ为1 时，换能器就成为了一个压电陶瓷圆管。计算λ= 0～1 时，结果如图8所示。由图8可以明显看出：换能器径向振动的固有频率随换能器壁厚比的增大而降低。这可能是因为压电陶瓷材料的弹性模量比金属材料的弹性模量要小，当换能器的壁厚比变大时，相当于换能器中压电陶瓷材料所占比例变大，因此固有频率会变小。

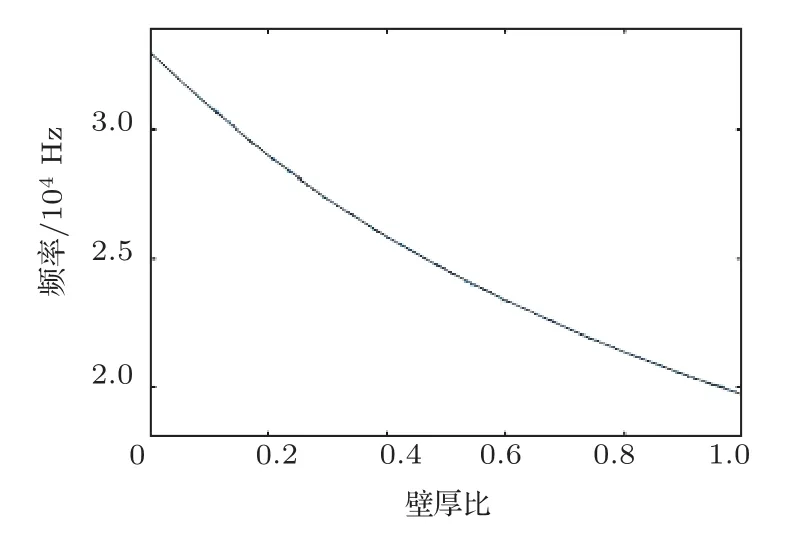
图8 固有频率与壁厚比的关系Fig.8 Relationship between natural frequency and radius ratio

6 结论

(1)本文以由径向极化的压电陶瓷圆管与金属预应力管沿径向复合而成的二元压电陶瓷复合换能器为例，验证了有限差分法在计算压电陶瓷复合超声换能器固有频率方面的可行性及准确性。有限差分法可以大大缩短数学推导过程，简化公式复杂程度和计算机编程过程。

(2)推导了换能器径向振动的数学模型及其有限差分形式，给出了径向振动的特征方程。通过对计算实例固有频率的计算验证可知：对换能器所取离散节点处越多，计算结果越接近真实值，但会增加计算时长，需取用合适的节点处进行理论计算。

(3)通过对不同结构尺寸的换能器径向振动固有频率的计算可知：换能器径向振动的固有频率随压电陶瓷圆管内径的增大而降低，随换能器壁厚比的增大而降低。

(4)本文所建立的换能器径向振动固有频率的有限差分法具有一定的通用性，同样适用于结构形式相近的换能器及其他元器件。