基于LPP模型的供应商分类方法及其在电力企业中的应用
王婧婷,邹俊荣,刘 锐,陶新民
(东北林业大学 工程技术学院,哈尔滨 150036)
0 引 言
随着经济全球化和知识经济时代的到来,供应链管理受到越来越多的关注,导入、实施供应链管理,建立企业高效运作、快速响应的供应链机制,创造供应链的协同效应已成为企业提升核心竞争力、获得竞争优势的重要途径。供应商是供应链中物流的始发点、资金流的起点和信息流的终点,选择合适的供应商并成立供应商分类小组对合格供应商的各项资格或条件进行分析及审议,对于供应链的核心企业而言显得尤为重要[1]。
在企业供应商的选择中,比较常用的方法:线性权重法、层次分析法、ABC成本法、数据包络法、主元成分分析(Principal Components Analysis,PCA)法等。其中,PCA法在供应商评价中应用最为广泛[2-4]。然而,实际中企业供应商的各项指标间的关系都是非线性的,所以采用传统的PCA法是不妥的。因此,需要一种能够在对供应商进行定量评价过程中突破评价指标间的相关性关系的限制、通过简便的方法快速对企业供应商进行分类评价的方法。
局部保持投影(Locality Preserving Projection,LPP)是非线性方法Laplacian Eigenmap的线性近似,作为一种新的子空间分析方法,它既能解决PCA法难以保持原始数据非线性流形的问题,又能弥补非线性方法难以获得新样本点低维投影的缺点,还能保持原数据结构的局部关系[5]。目前,LPP在人脸识别、图像检索等领域得到了广泛应用[6-8],而在供应商企业分类评价领域的应用尚未见报道。该文拟将LPP分析法应用到企业供应商的分类中,使其既能够实现PCA法的降维,又能够保持原数据结构的局部关系。
以电力企业为例,结合中国电力企业的现状,通过LPP算法降维对各项指标定量分析,全面客观地对企业供应商进行分类,从而为提升电力企业管理的质量提供借鉴[9]。
1 LPP模型分析
已知数据集x1,x2,…,xM,其中xi∈RN,(i=1,2,…,M),M为样本总数,N为指标总数。设原始空间为X,映射后的空间为Y,xi、xj为原始空间下的坐标,yi、yj为新基向量投影下的坐标。在总体样本中考虑,原来相近样本的xi、xj在新的基坐标空间中也同样相近。应用高斯核函数wij(i,j=1,2,3…,M)表示原有样本空间的相近程度为
(1)
式中:xi在xj最近K邻内或xj在xi最近K邻内;σ为高斯核函数相关系数;K为最近邻个数。
为了求得最佳的投影方向矩阵,需要在一定的约束条件下使投影方向的目标函数最小化,最佳投影方向的目标函数为
minw‖yi-yj‖2wij
(2)
由式(2)进一步推导可得:
式中:V∈RN×1是标准基向量,且yi=VTxi,yj=VTxj。
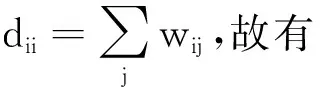
(3)
由式(3)推导得:
VTXDXTV-VTXWXTV=VTX(D-W)XTV=
VTXLXTV
式中:V∈RN×1;xi、xj∈X∈RN×M;W∈RM×M;D∈RM×M;L=(D-W)是拉普拉斯矩阵。
为了防止0解出现,加上约束条件:
yDyT=1
最佳投影方向的目标函数为
(4)
式(4)可用拉格朗日乘子法求解,即:
L(V,λ)=VTXLXTV-λ(VTXDXTV-1)
(5)
式(5)对V求偏导得
令2XLXTV-2λXDXTV=0,则有
XLXTV=λXDXTV
(6)
令A=XLXT,B=XDXT,求使方程AV=λBV有非0向量解的λ。此处A为N阶实对称矩阵,B为N阶实对称正定矩阵,V为N维列向量。称AV=λBV为矩阵A相对于矩阵B的广义特征值问题,称满足式(6)要求的λ为矩阵A相对于矩阵B的特征值,而与λ相对应的非0向量解V称为属于λ的特征向量。
LPP分析法通过求取式(6)中的特征问题的特征值λ和特征向量V,并将求得的特征向量V升序排列,以求得样本矩阵X在前p个最小特征值λi(i=1,2…,p)对应的特征向量Vi(i=1,2…,p)上的投影Y=[V1,V2,…,Vp]TX,从而实现数据的降维。
LPP模型的线性降维方法可以解决电力企业供应商分类繁琐的问题,根据目标函数最小时降维效果最佳的特点对电力企业供应商进行分类。此外,基于LPP模型的供应商分类方法具有相容性,除电力企业外同样适用于其他企业的供应商分类。
供应商的选择是决定企业成本及产品质量的重要因素。应用LPP模型的层次分类方法来解决供应商选择评价问题,具体步骤如图1所示。
2 数据实验
为了验证基于LPP分析的企业供应商分类方法的通用性及有效性,分别进行以下两种实验。
2.1 实验一
对国内某大型电力企业的轴承供应商进行评价。
通过与该企业工作人员进行访谈和问卷调查的方式得到该企业有关供应商的评价准则,根据各评价准则绘制层次图,如图2所示。
图2中,技术能力、产能和管理水平为产出指标,报价、响应时间和离岸品质为投入指标。为方便比较, 将各供应商评价指标进行标准化处理,标准化后的24个供应商的评价指标如表1所示。
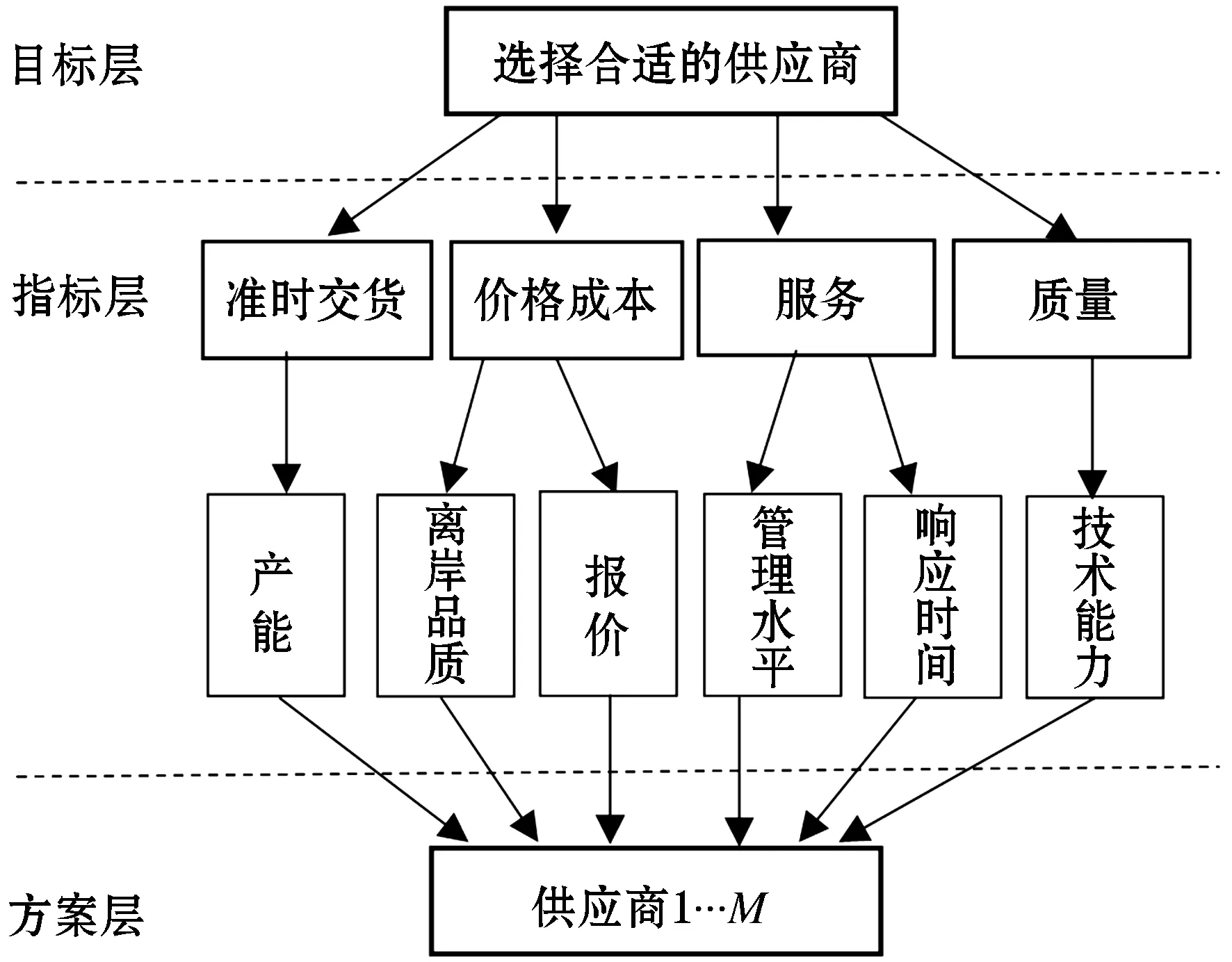
图2 轴承供应商评价准则层次图
将投入指标取倒数并作最大、最小化处理,得到处理后的供应商指标如表2所示。人为定义最好的供应商和最差的供应商,分别为工厂1和工厂2。
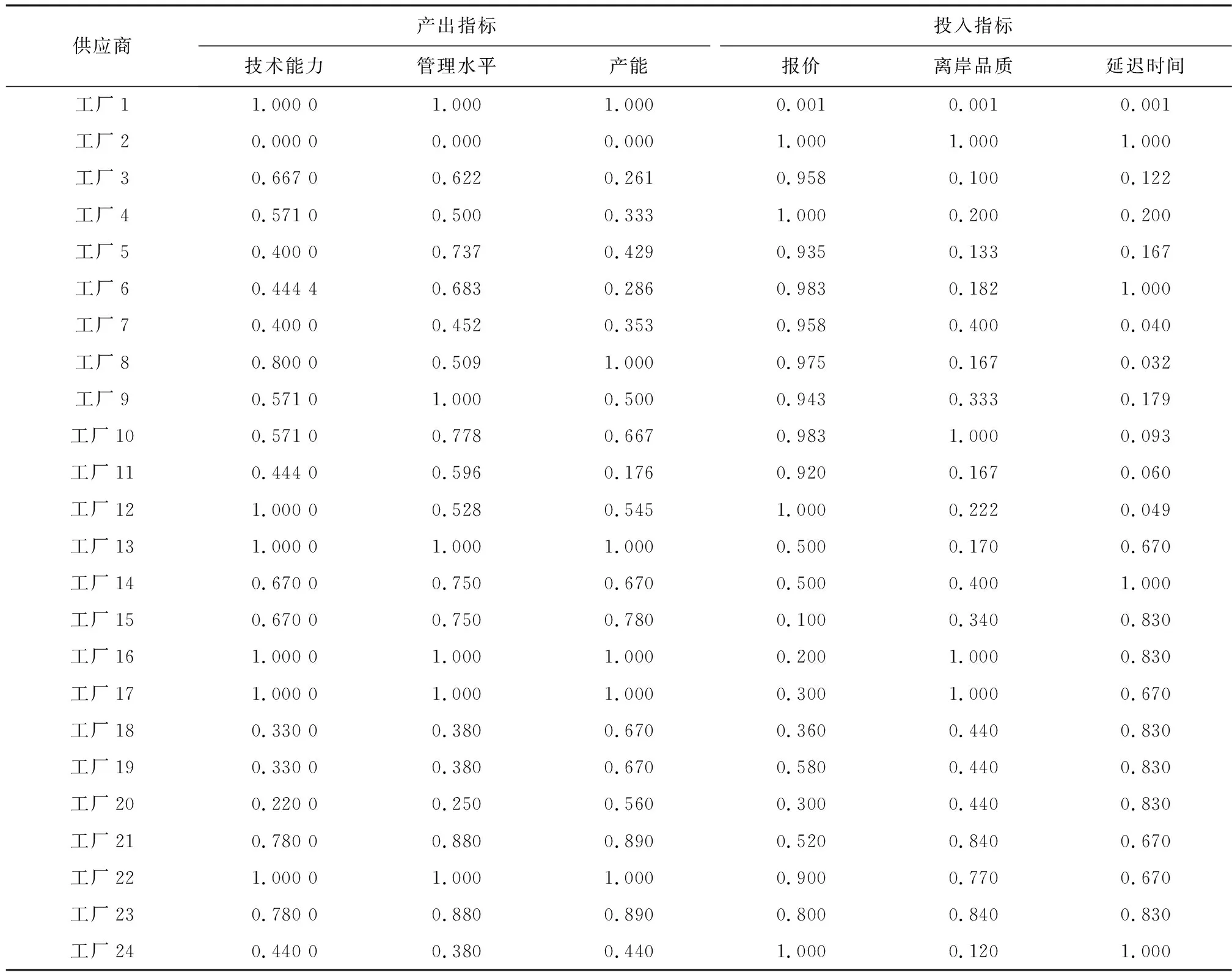
表1 标准化后的轴承供应商评价指标

表2 处理后的轴承供应商指标
由于各评价指标的量纲不同,因此指标不能直接相加;同时,各指标间存在一定的相关性,直接相加会增加信息的重叠。为了说明各个指标间具有一定相关性,采用巴特利特球形检验法进行自相关性检验。假设指标数据的自相关系数矩阵为单位阵,如图3所示,显著水平设置为0.05,通过SPSS软件统计整理得评价指标的显著性概率P<0.05,数据呈球形分布,认定指标数据具有一定的相关性。
为验证LPP分析方法的合理性,根据上述数据,利用相关专家评定的方法得出最佳评价结果,利用Jaccard相似性系数[10]绘制相似性系数变化图,进行比较分析,其中Jaccard相似性系数定义为
(7)
式中:f00代表具有不同的类和不同的簇的对象个数;f01代表具有不同的类和相同的簇的对象个数;f10代表具有相同的类和不同的簇的对象个数;f11代表具有相同的类和相同的簇的对象个数。
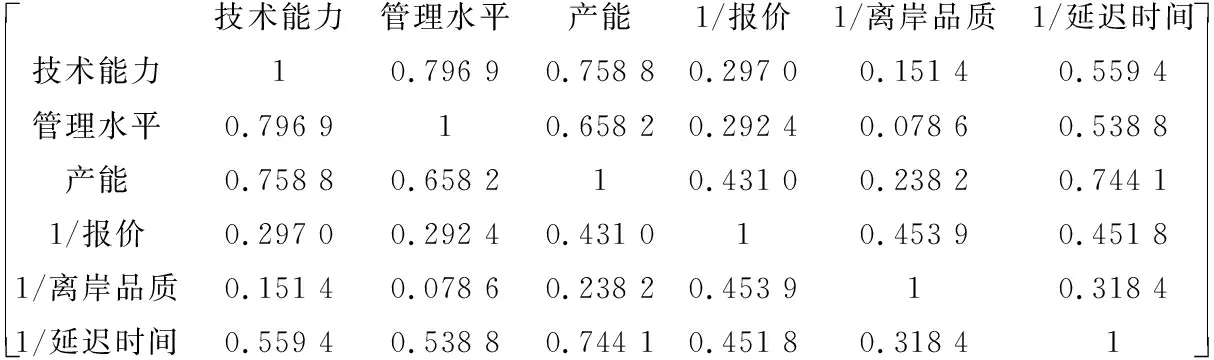
图3 轴承供应商自相关系数矩阵
取固定的最近邻个数K=6,得出Jaccard相似性系数随高斯核参数的变化图,如图4所示。
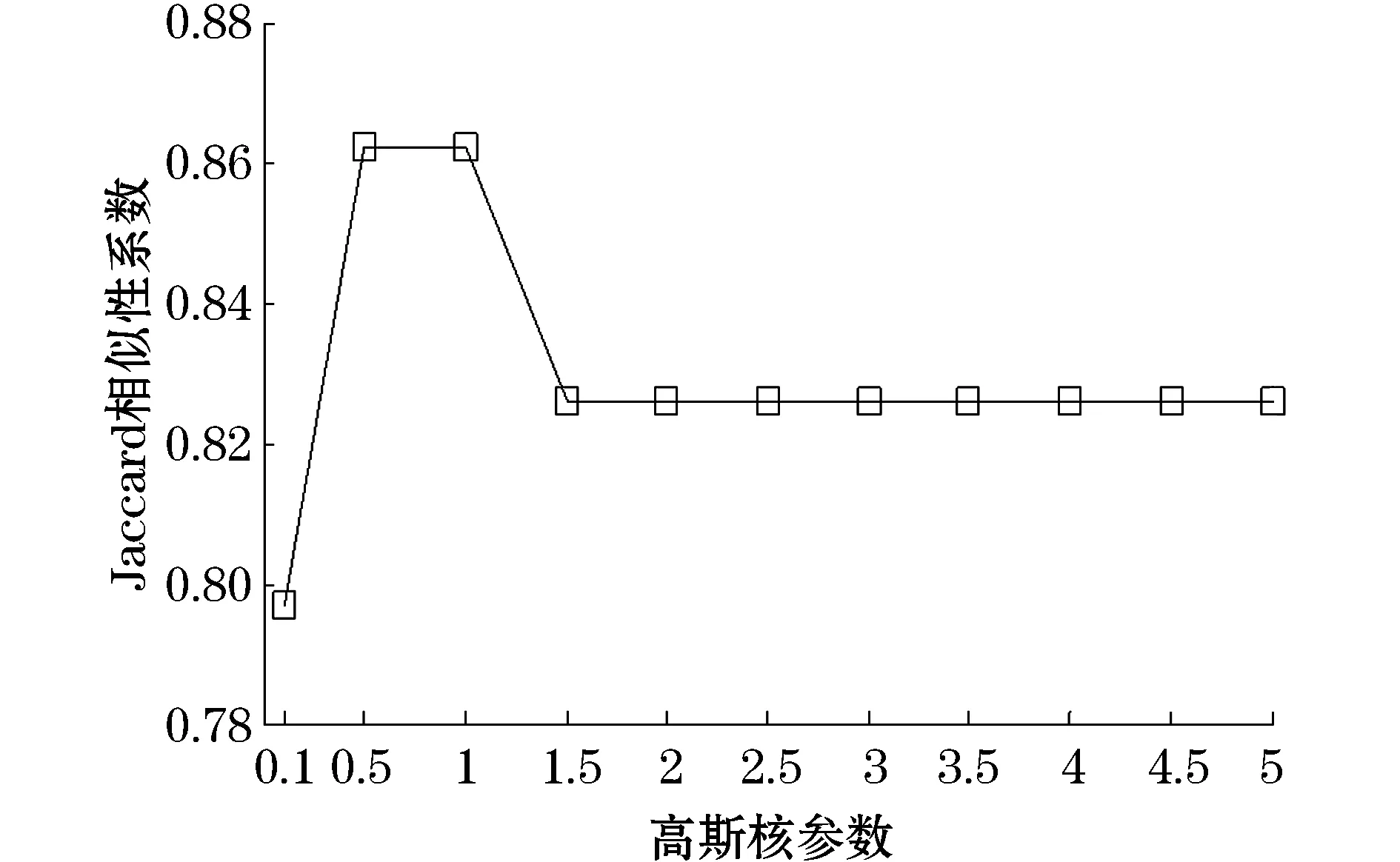
图4 Jaccard相似性系数随高斯核参数的变化
从图3中可以看出,当K=6时,高斯核参数σ=0.5~1,较为合理。同理,固定高斯核参数σ=1,得出Jaccard相似性系数随最近邻个数的变化图,如图5所示。
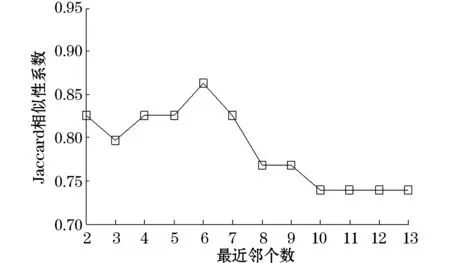
图5 Jaccard相似性系数随最近邻个数的变化
从图5中可以看出,当高斯核参数σ=1时,最近邻个数K=6,较为合理。
确定相关系数后,利用LPP进行降维,选择高斯核函数相关系数σ=1,最近邻个数K=6,求得特征值与特征向量,并对特征值进行升序排列。选择最小的特征值并求取样本矩阵在对应特征向量上的投影,对分组计算结果进行排序,如表3所示。
综合指标共分为优、良、中、差4组。根据原始数据的比较结果以及相关专家的评定可知,利用LPP分析法得出的结果与标准结果是一致的。所以针对该实例,选取高斯核参数σ=0.5~1,最近邻个数K=6进行LPP分析是较为合理的。

表3 轴承供应商综合指标排序
2.2 实验二
对国内某大型家具企业的木材供应商进行评价。
同样通过与该企业工作人员访谈和问卷调查的方式得到该企业有关供应商的评判准则,评价指标分为5大类共13个细类,根据各指标绘制层次图,如图6所示。
1)企业信誉风险:①订单完成率,即该供应商交货成功的次数与订单总次数的比率;②服务满意率,指供应商在供应的全过程中企业对所提供服务的满意状况;③企业名誉与地位,指供应商在同一行业中的影响力。
2)合作能力:①准时交货率,即从时间的角度考察供应商的交货能力;②订货满足率,即从数量方面考察供应商交货能力;③合约信任度,是反映供应商的可信任程度的指标。
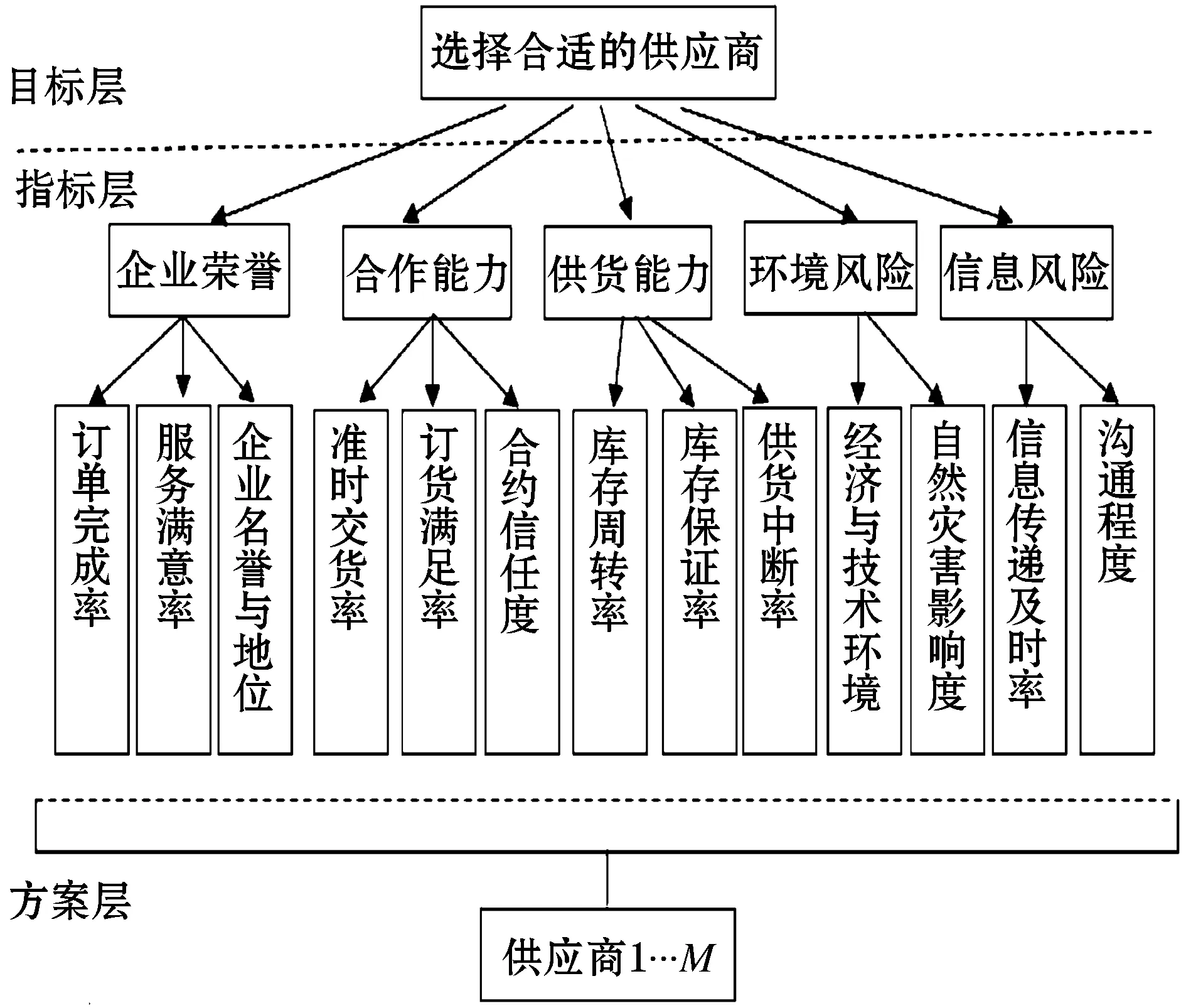
图6 木材供应商评价准则层次图
3)供货能力: ①库存周转率, 指一定时期内企业销售成本与存货平均资金占用额的比率;②库存保证率,是反映库存能否保证生产要求的指标;③供货中断率,反映供应商到制造商2个节点之间配送的可靠程度。
4)环境风险:①经济和技术环境;②自然灾害影响度。
5)信息风险:①信息传递及时率,即数据及时传送的次数占传送总数的百分比;②沟通程度,即合作过程中制造企业与供应商进行沟通和交流的频繁程度以及双方所采取的沟通方式。
图6中,投入指标为供货中断率和自然灾害影响度,其余为产出指标。同样对数据进行标准化处理,标准化后的24个供应商评价指标如表4所示。将投入指标取倒数并作最大、最小化处理,得到供应商指标如表5所示。为了显著的地说明排序效果,人为定义最好的供应商和最差的供应商,分别为工厂1和工厂2。
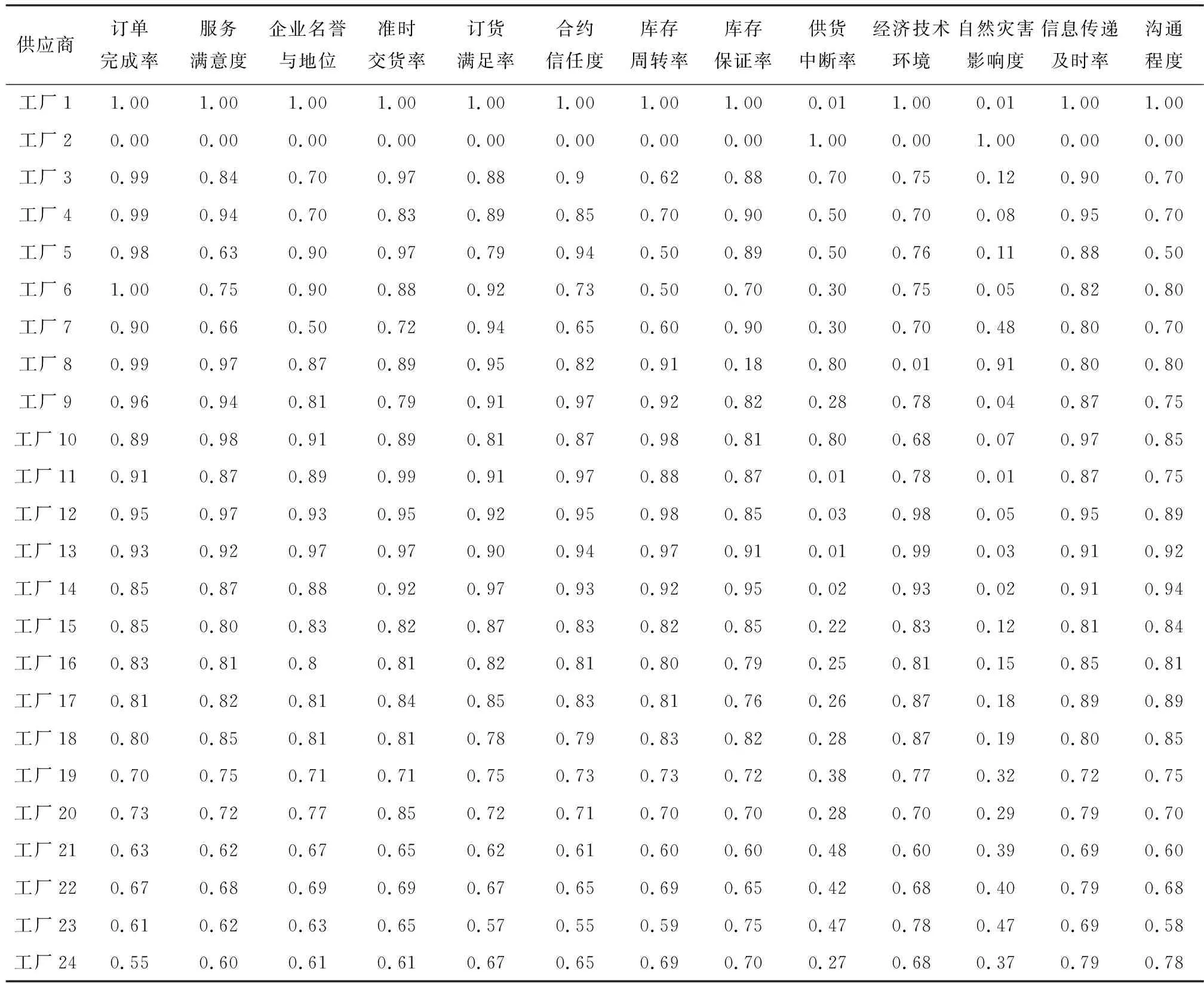
表4 标准化后的木材供应商评价指标
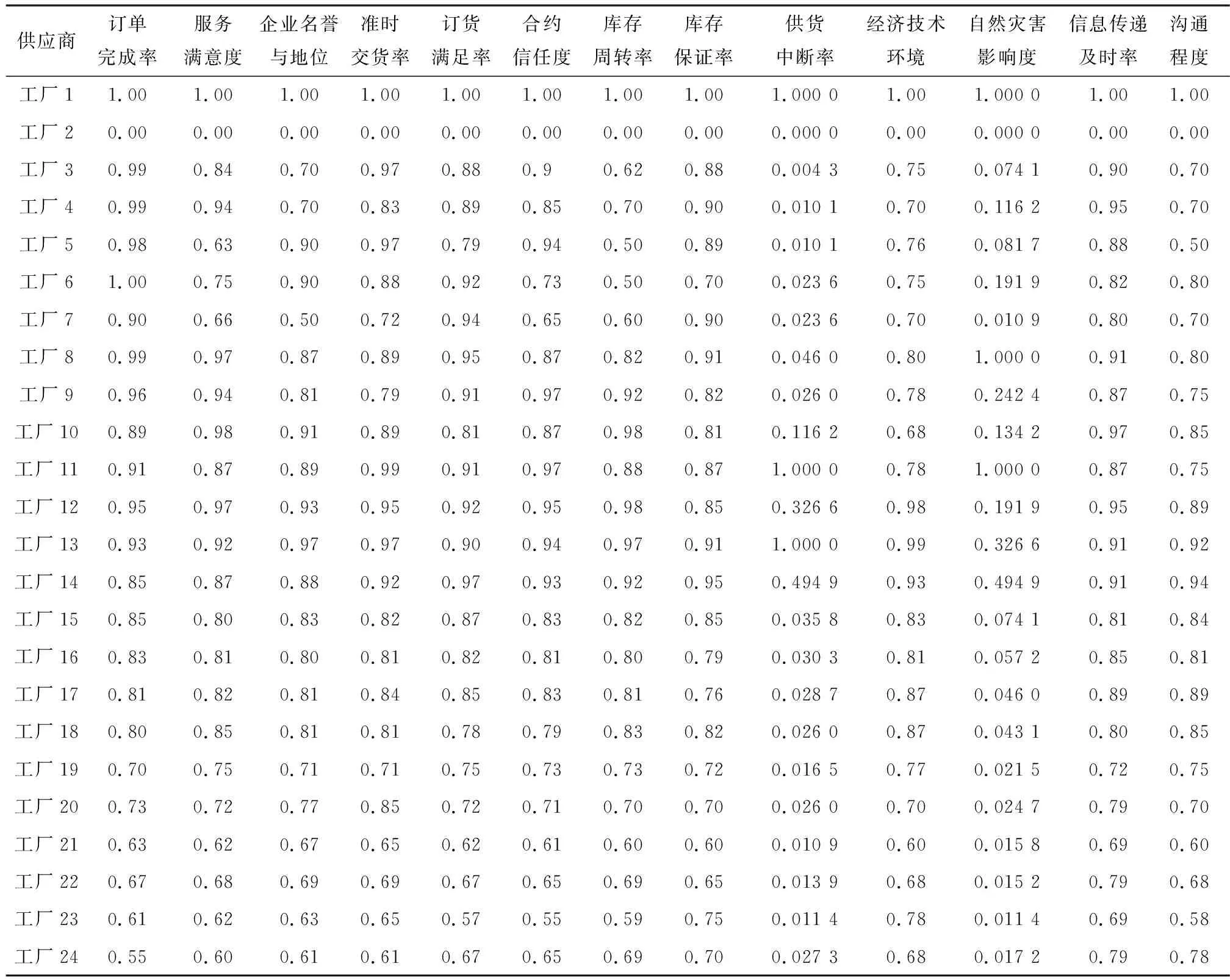
表5 处理后的木材供应商评价指标
同样,各指标量纲不同且指标间存在一定相关性,各指标不能直接相加。假设指标数据的自相关系数矩阵为单位阵,如图7所示,显著水平设置为0.05,通过SPSS软件统计整理得评价指标的显著性概率P=0<0.05,认定指标数据具有一定的相关性。
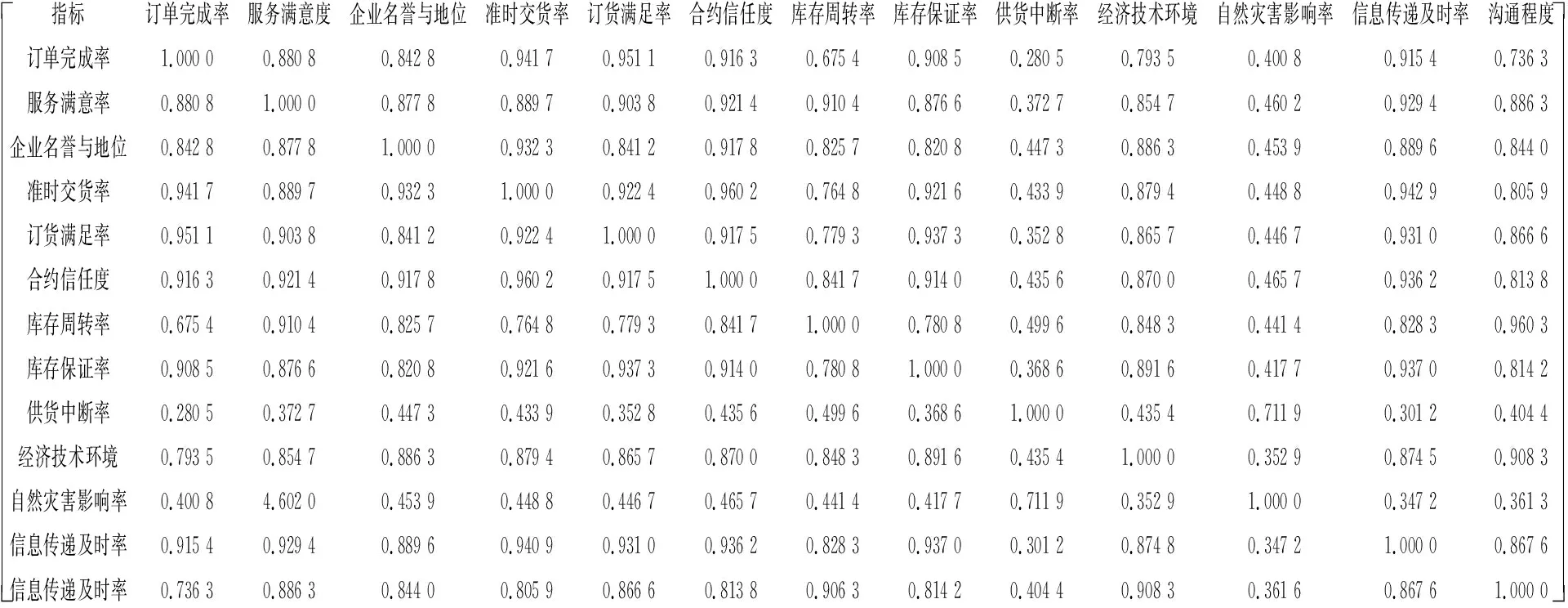
图7 木材供应商自相关系数矩阵
通过上述所得数据验证LPP分析方法的合理性,同样利用Jaccard相似性系数并绘制相似性系数变化图,进行比较分析。
取固定的最近邻个数K=6,得出Jaccard相似性系数随高斯核参数的变化图,如图8所示。
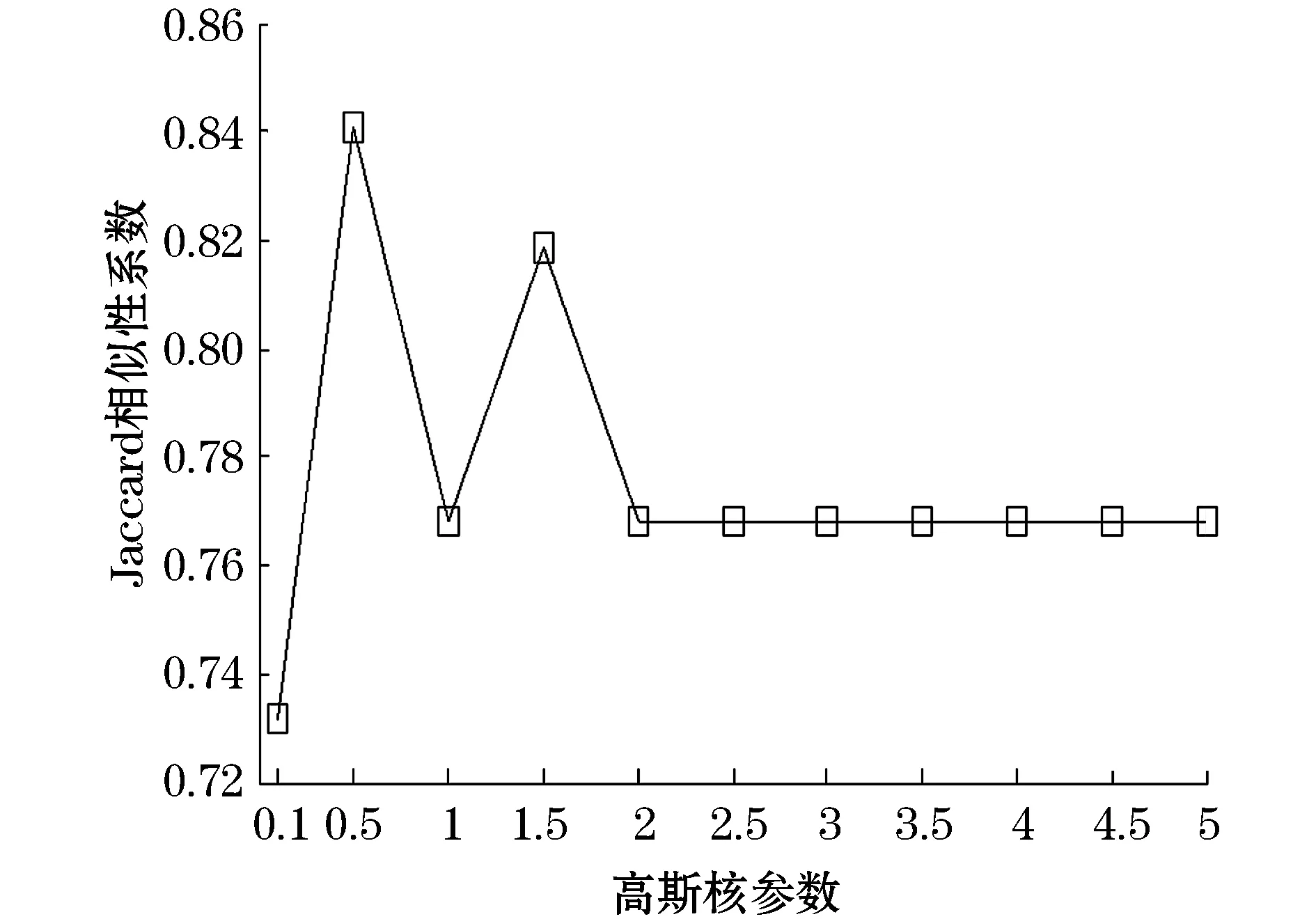
图8 随高斯核参数变化的Jaccard相似性系数
从图8中可以看出,当K=6时,高斯核参数σ=0.5~1.5,较为合理。同理,固定高斯核参数σ=0.5,得出Jaccard相似性系数随最近邻个数的变化图,如图9所示。
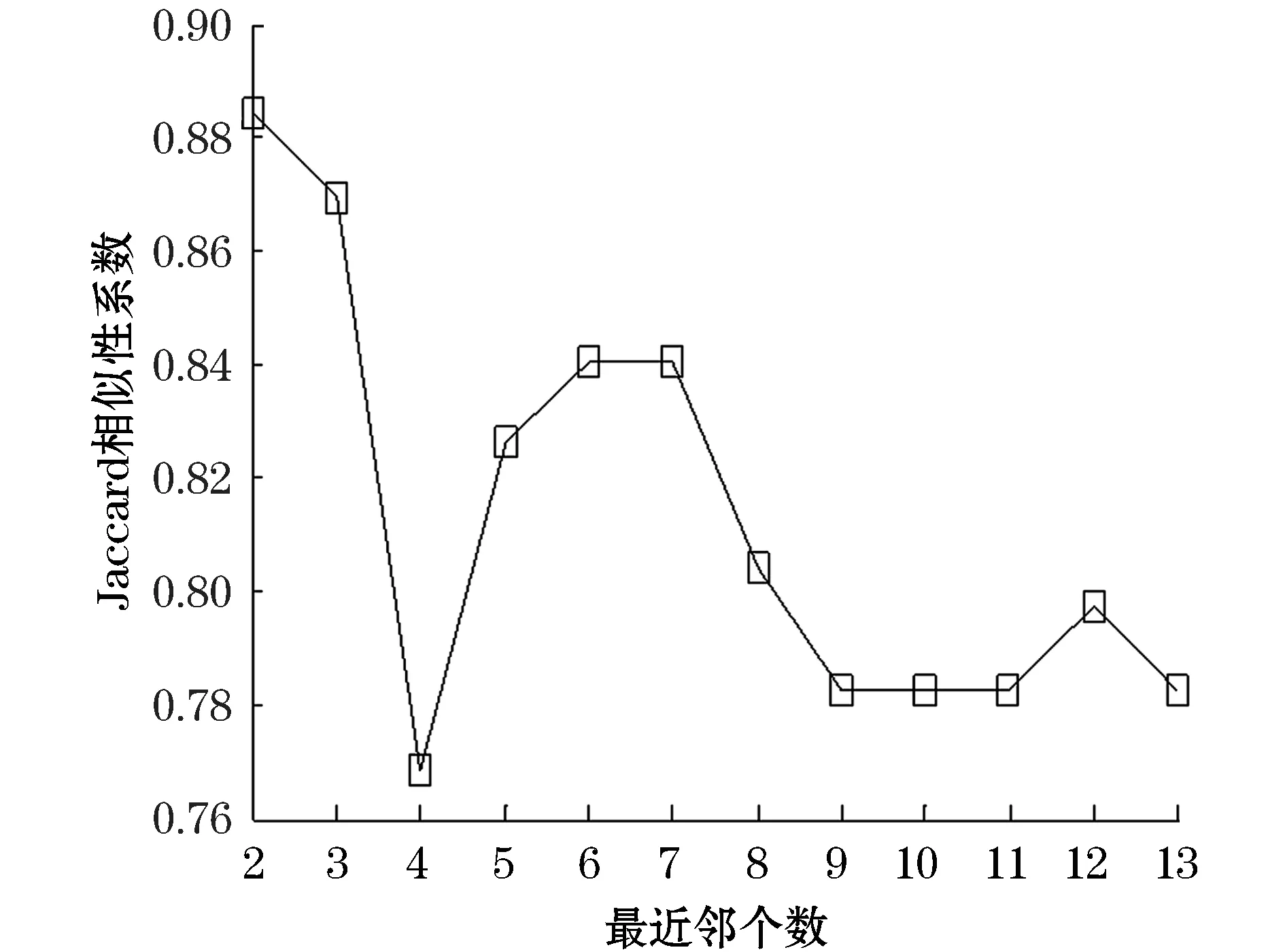
图9 随最近邻个数变化的Jaccard相似性系数
从图中9可以看出,当高斯核参数σ=0.5时,最近邻个数K=2~6,较为合理。
确定相关系数后,利用LPP进行降维,选择最近邻个数K=6,求得特征值与特征向量后对特征值进行升序排序,排序分组计算结果如表6所示。
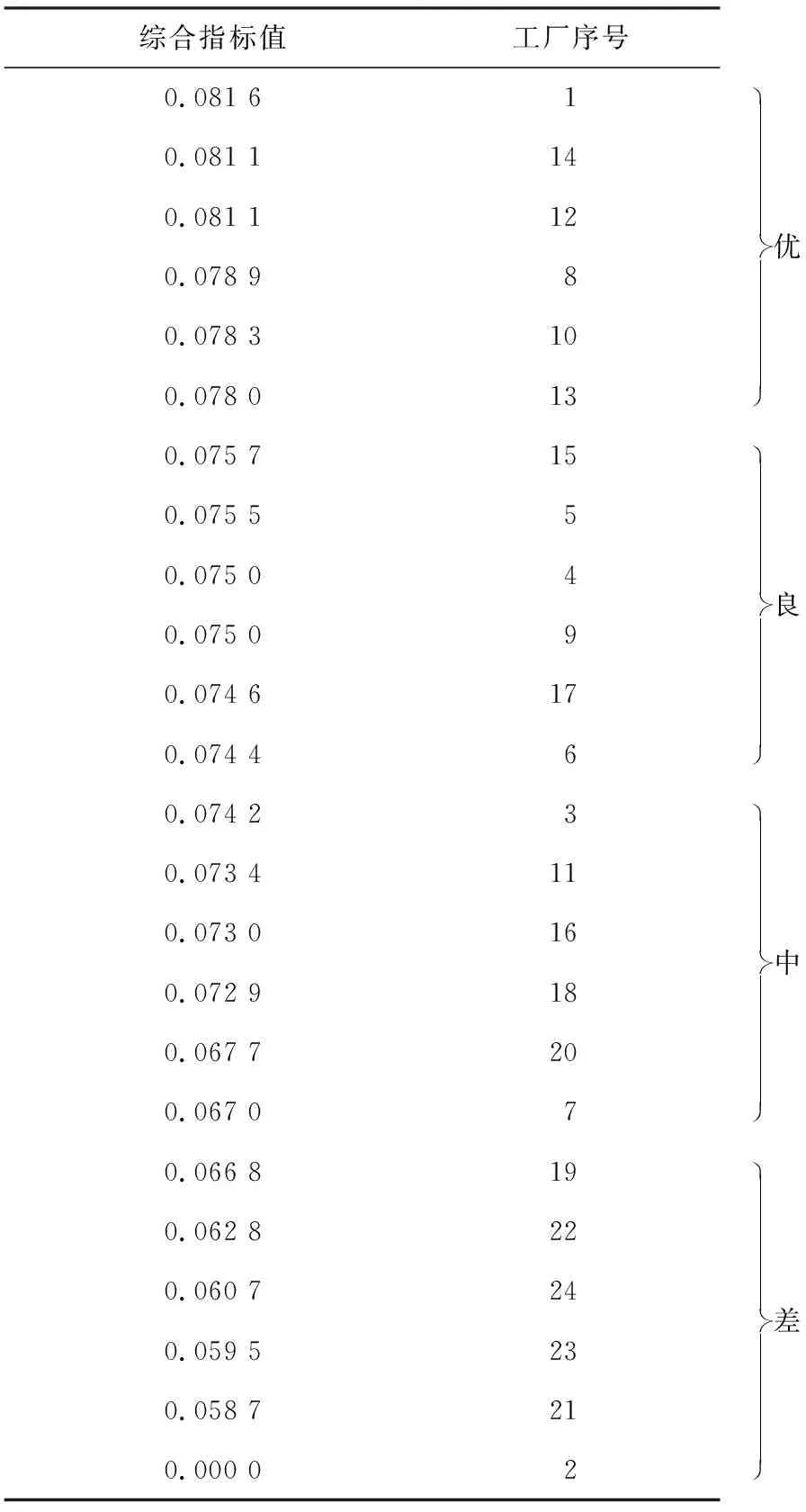
表6 木材供应商综合指标排序
综合指标共分为优、良、中、差组类。通过分析可知该实例选取高斯核参数σ=0.5~1.5,最近邻个数K=2~6进行LPP分析是合理的。
3 分析总结
为了验证LPP算法对供应商分类的有效性,文章对轴承及木材供应商进行分类,并采取了以下几个步骤进行分析。
首先,通过访问和问卷调查的方式获取供应商的评判准则并分类;其次,使用LPP算法对获取的数据进行分析,选用不同的参数进行比较、调试;最后,选用Jaccard相似性系数表示参数选择结果的拟合程度。通过与专家给出的标准评价结果进行对比分析,得出基于LPP分析的企业供应商分类方法在应用时选取高斯核参数σ=0.5~1.5和最近邻个数K=2~6评价的结果是较为合理的。
4 结 语
1)基于LPP分析的企业供应商分类方法不仅适用于电力企业供应商,对于其他企业的供应商分类也同样适用,能够更加有效地解决供应商分类问题。
2)基于LPP分析的企业供应商分类方法,是一种通过对各项指标进行定量分析,从而全面客观地对企业供应商进行分类的方法。所采用的指标分为产出指标和投入指标,使得供应商的评价结果更加全面、真实、客观。
3)基于LPP分析的企业供应商分类方法应用LPP方法而非传统的PCA法实现坐标投影变换,不受指标间线性相关与非线性相关关系的限制,过程更为简便,降维作用更加明显。
4)基于LPP分析的企业供应商分类方法,在降维的同时保持了各供应商之间的局部结构信息的关系,较PCA法更适合于供应商的分类。

