基于Matlab的输电线路故障测距仿真分析

李清泉，杨茂亭，冯知海

(国网山东省电力公司检修公司，济南 250000)

0 引 言

为了实现电能的优质分配和传输，智能电网的规划建设问题得到了社会各界的广泛关注。而输电线路作为传输电能的载体，一旦发生故障，轻则影响人民的日常生活，重则带来经济损失和生命危险。而且，输电线路绵延数十公里到数百公里不等，在发生故障时，即使进行大量的巡线工作也难以在第一时间找到故障点进行修复。因此必须借助故障录波装置进行准确的故障测距，以保证能够及时修复受损的输电线路，使得电力系统能够在一定的经济指标和安全指标内运行[1-2]。但是，目前故障录波装置中采用的故障测距算法还存在着很多不足，如不能完全消除过渡电阻、系统阻抗等因素对测距结果造成的误差等。所以有必要对故障录波器的测距算法进行分析和改进，以提高测距结果的计算精度[3]。为此，本文深入分析了输电线路测距算法的误差来源，并对改进前后的测距算法在Matlab/Simulink环境下进行了对比分析，验证了所做工作的有效性。

1 滤波算法的研究和仿真

不管电力系统发生何种类型的故障，故障电流中都将出现衰减的直流分量和高次谐波分量，谐波频率最高可达2 kHz。对于输电线路故障录波器而言，其采样频率至少设置为4 kHz才能保证采样信号的完整还原以及防止频率混叠现象的发生[4]。但是，如此高的采样频率不仅对故障录波器的微处理器和AD转换器的性能提出了过高的要求，采样信号还容易受到外界的干扰，造成系统紊乱。所以故障录波器滤波效果的优劣直接决定了故障时电压电流基波分量值的准确性，进而影响测距算法的精度和准确性。为此，深入分析傅里叶算法的误差来源，并提出有效的改进措施。

1.1 傅里叶算法误差分析

当原始信号X(t)中含有衰减的直流分量时，则：

式中：A为衰减的非周期分量的幅值；τ为衰减的时间常数；Xn为n次谐波有效值。

所以，当考虑衰减的非周期分量的幅值对计算结果的影响时，利用常规傅里叶算法得到的正弦项幅值an和余弦项幅值bn由于增加了衰减的非周期分量而转换成以下形式：

可以看出，正弦项和余弦项幅值的增量Δan和Δbn对信号幅值和相角的计算将产生较大的误差。而这种误差正是由于常规傅里叶算法不能消除衰减的直流分量导致的。因此，在利用常规傅里叶算法求取电压电流的有效值时，就需要对其进行改进，以消除衰减的直流分量对计算结果造成的影响。

1.2 差分傅里叶算法

差分傅里叶算法可以在不提高计算工作量的前提下，将测距结果的误差保持在合理的范围之内[5-6]。在采用差分算法对傅里叶算法进行改进时，可以将离散的采样值做差值x[n+1]-x[n]，来替换傅里叶变化中的采样值x[n]，然后再按照傅里叶算法的原理求取各次谐波的正弦项幅值an和余弦项幅值bn，进而利用此值完成各次谐波有效值Xn和相位角θn的计算。

tanθn=bn/an

在傅里叶算法中增加差分环节虽然可以在一定程度上消除直流分量和非周期分量对计算结果的影响，但是却使得高次谐波的幅频响应得到增强。所以需要在故障录波装置的数据采集通道中设置模拟低通滤波器来消除高次谐波分量。常用的二阶RC滤波器如图1所示，其幅值传递式如式(1)所示。

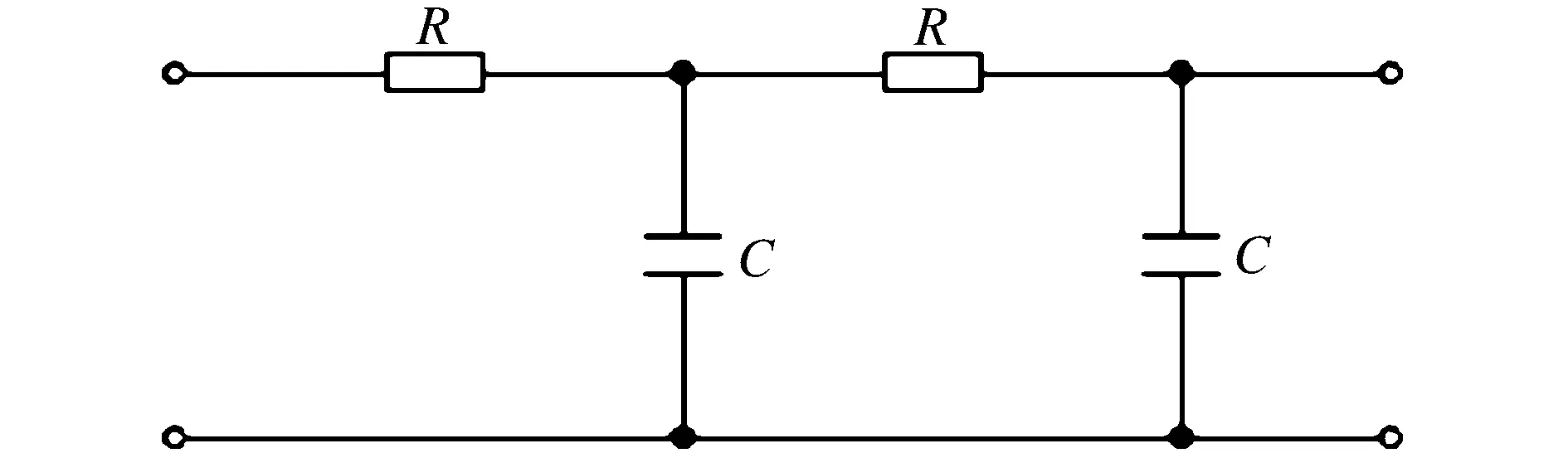
图1 模拟低通二阶滤波器

(1)

当R取值4.7 kΩ，C取值0.1 uF时，该二阶RC滤波器的幅频响应曲线如图2所示。

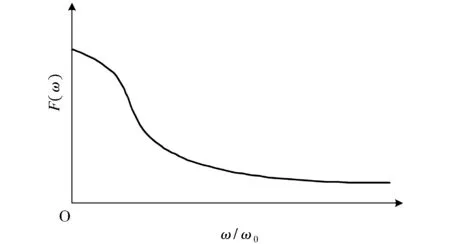
图2 二阶RC滤波器的幅频特性曲线

从图2可以看出，二阶RC滤波器的幅频特性是单调衰减的，对于高次谐波的衰减程度更大。这正好抵消了差分滤波环节对高次谐波幅值响应的影响。因此，在模拟低通滤波器和数字滤波器(差分傅里叶算法)的共同作用下，可以大大提高所需电量的计算精度。

1.3 仿真分析

在Matlab环境下，设置模拟信号如下：

Va=50+50exp(-10t1)+100sin(2pi*50*t1)+30*sin(4*pi100*t1)+10*sin(8*pi*100*t1)

通过仿真，利用常规傅里叶算法计算的基波幅值如图3所示，而差分傅里叶算法计算的基波幅值如图4所示。对比图3和图4可以发现，利用差分傅里叶算法来求取信号的有效值时，其有效值摆动的幅度和趋于稳定的时间都明显减小。原因是衰减的直流分量对应的信号频谱为连续谱，并与原始信号中基频分量的信号频谱产生了混叠现象。当利用差分环节将衰减的直流分量剔除后，计算效果得到明显加强。

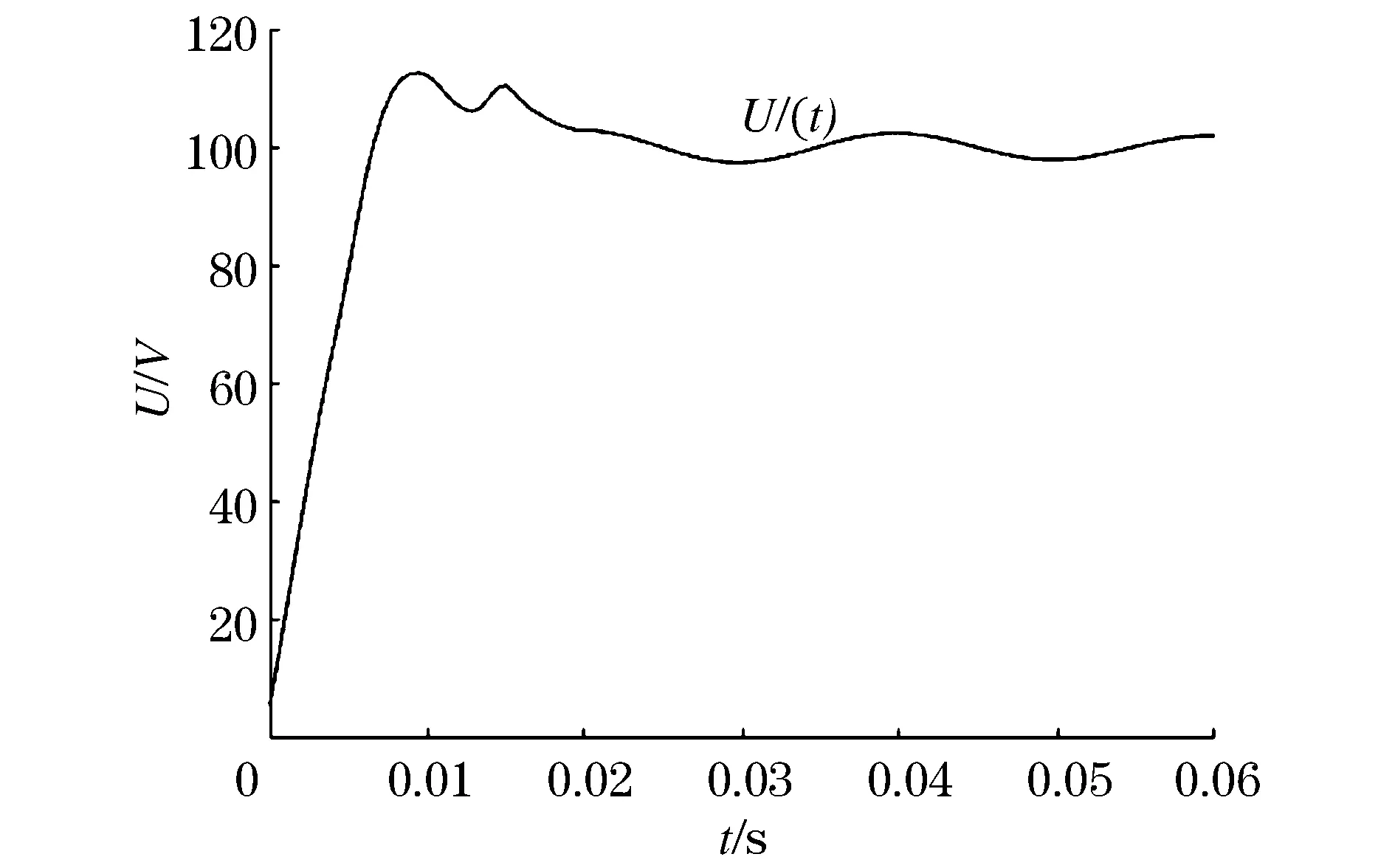
图3 常规傅里叶算法计算的基频幅值图

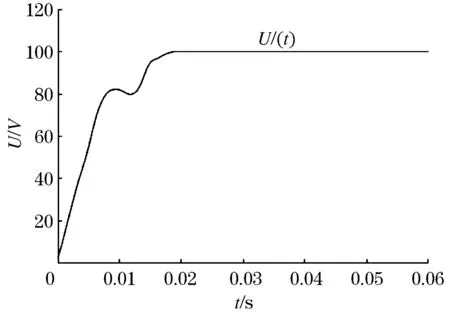
图4 差分傅里叶算法计算的基频幅值图

2 单端故障测距算法

单端故障测距算法是以输电线路的电源端为测量端，利用本侧的电压和电流信息求得故障点到测量端的阻抗，进而利用线路单位阻抗和输电线路长度之间的比例关系求得故障距离[7]。对于均匀的输电线路，利用其进行故障测距时所得的测距结果误差较小。但是，在实际的电力系统中，输电线路并不是完全对称的，而且故障电阻一般不为0，自然都会使故障测距结果产生误差，严重时误差范围远大于系统允许值。

2.1 基本原理及误差分析

在均匀的输电线路中，总阻抗等于单位阻抗与输电线路长度的乘积。因此，在求得了故障点到测量点的总阻抗后，可以根据比例关系求得故障距离。根据此原理，假定在图5所示的双电源供电系统中发生故障时，对于测量端m而言，其测量到的理论电抗值如式(2)所示。

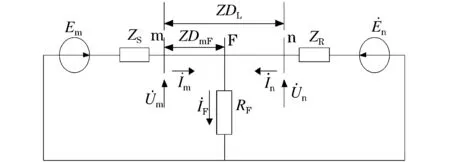
图5 单相系统线路内部故障情况

(2)

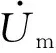
通过对式(2)进行分析得出：

1)当过渡电阻RF=0时，ΔZ=0，则测量阻抗Zm=ZDmF，测量结果准确；

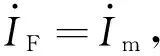
2.2 误差解决分析

对于单电源供电系统，考虑到此时的测量误差为纯电阻性质ΔZ=RF，测量阻抗为Z=R+jX。那么忽略测量阻抗的电阻部分，仅仅分析电抗部分就可以消除过渡电阻对测量阻抗造成的影响，即：

Im[Zm]=Im[ZDmF+RF]

所以对于均匀输电线路，根据其单位电抗X和总电抗Xm之间比例关系求得故障距离DmF，如式(3)所示。

Xm=XDmF

(3)

2.3 仿真分析

在Matlab/Simulink环境下搭建了35 kV的单端供电系统：系统阻抗ZS=0.788∠70.6°；输电线路的总长度L=50 km；输电线路的单位阻抗zL=0.131+j 0.372 Ω/km；负荷参数P=272 MW、Q=95.8 MW。

在仿真过程中，以A相在0.06 s发生短路接地故障为例进行仿真测试，设置电力系统的采样频率fs=1 000 Hz。对于故障点而言，令其距离m端的距离分别为10 km、20 km和30 km，故障电阻分别为0 Ω、50 Ω和100 Ω。仿真结果如表1所示。

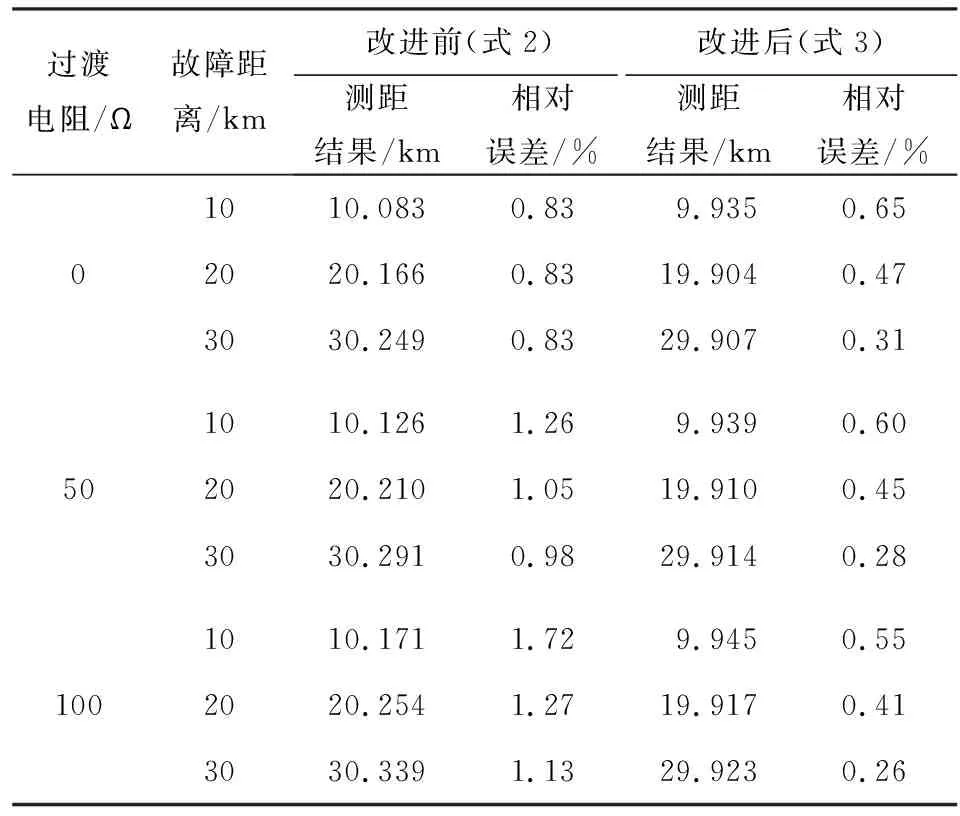
表1 过渡电阻对测距结果的影响

由表1的仿真结果可知，在线路发生金属性短路故障时，式(2)的测距精度较为理想，误差在1%范围内，但当过渡电阻和故障距离增大时，测距误差也相应增大；而式(3)的测距精度基本不受过渡电阻和故障距离的影响，其误差维持在0.7%范围内，其测距精度得到大幅提升。

3 双端故障测距算法

对于双端供电系统，特别是高压长距离输电线路等要求测距结果十分精准的场合，单端测距算法及其改进算法也无法消除过渡电阻等因素对测距结果造成的影响，因为测距误差较大而不能满足实际需要[8]。为此，可以引入对侧的电压和电流来提高故障距离的测量精度。

3.1 两端电流、一端电压法

对于图5所示的双端供电系统结构，以测量端m的电压电流和对端n的电流，进行双端故障测距算法的推导：

(4)

(5)

假定过渡电阻为纯电阻，可以根据单端故障测距算法的处理原则，对式(5)取虚部，可以得到：

(6)

将式(6)进一步化简得到故障距离DmF的表达式如下：

(7)

3.2 两端电流、两端电压法

同样对于图5所示的双端供电系统结构，以测量端m的电压电流和对端n的电压电流，进行双端故障测距算法的推导：

(8)

(9)

3.3 仿真分析

在Matlab/Simulink中搭建双端供电的110 kV系统，其各个元件的参数设置如下：

电源：Em=100∠20° kV，En=110∠0° kV,Zsm=Zsn=1.755+j 27.45 Ω；

线路：L=L1+L2=100 km，

Z2=2.75∠86.34° Ω/km，

c1=0.133 3 μF/km，

z0=10.485∠74.75° Ω/km，

c0=0.082 97 μF/km；

采样频率：fs=1 000 Hz。

当m侧和n侧进行同步采集数据时，在距m端xkm处发生，经过渡电阻100 Ω的A相接地故障，其中x范围为0～100，步长为10，其仿真测距结果如表2所示。

当m侧和n侧进行同步采集数据时，在距m端50 km处发生经过渡电阻Rg的A相接地故障，其中Rg范围为0～200 Ω，步长为20 Ω，其仿真测距结果如表3所示。

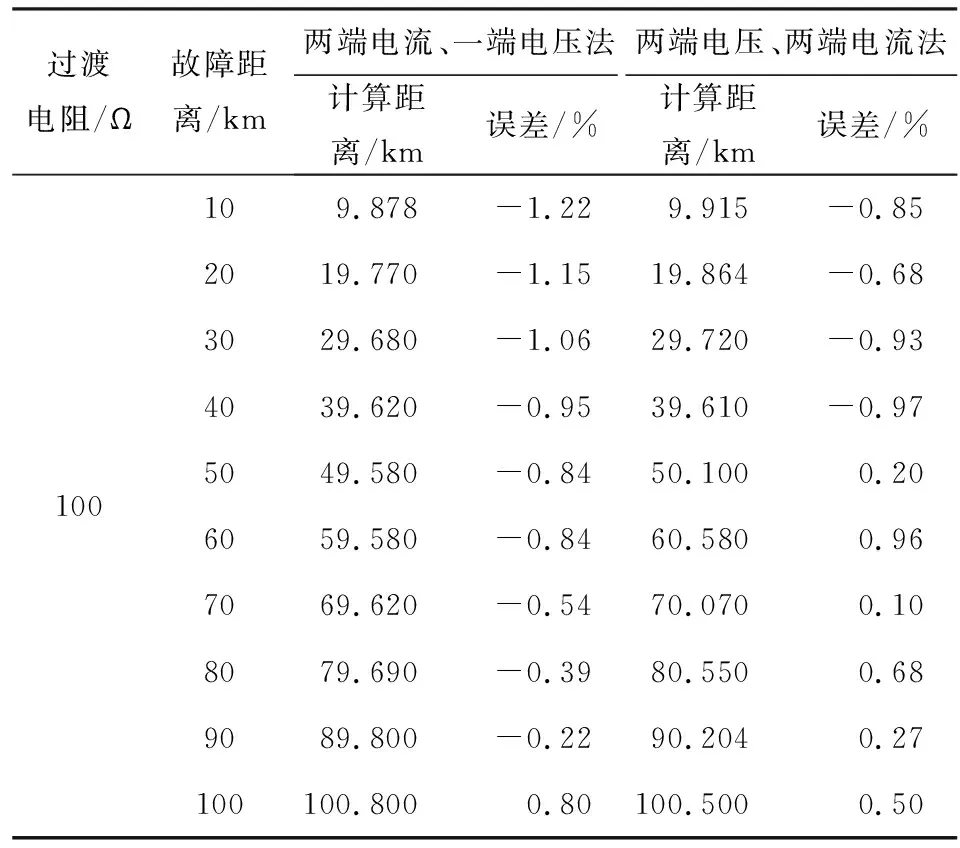
表2 Rg=100 Ω时的测距结果

对比表2和表3可知，同时利用输电线路m端和n端的电压电流信息进行故障测距时，测距结果在整条线路范围内几乎不受过渡电阻的影响。当故障点处的过渡电阻相等而故障位置不同时，式(7)的测距结果较式(9)的测距结果误差大，故障点距M母线较近时测距误差会大于1%；当故障发生的位置相同而接地电阻不同时，式(7)的测距结果虽然可以保证在1%误差范围内，但仍不及式(9)的测距结果精确。

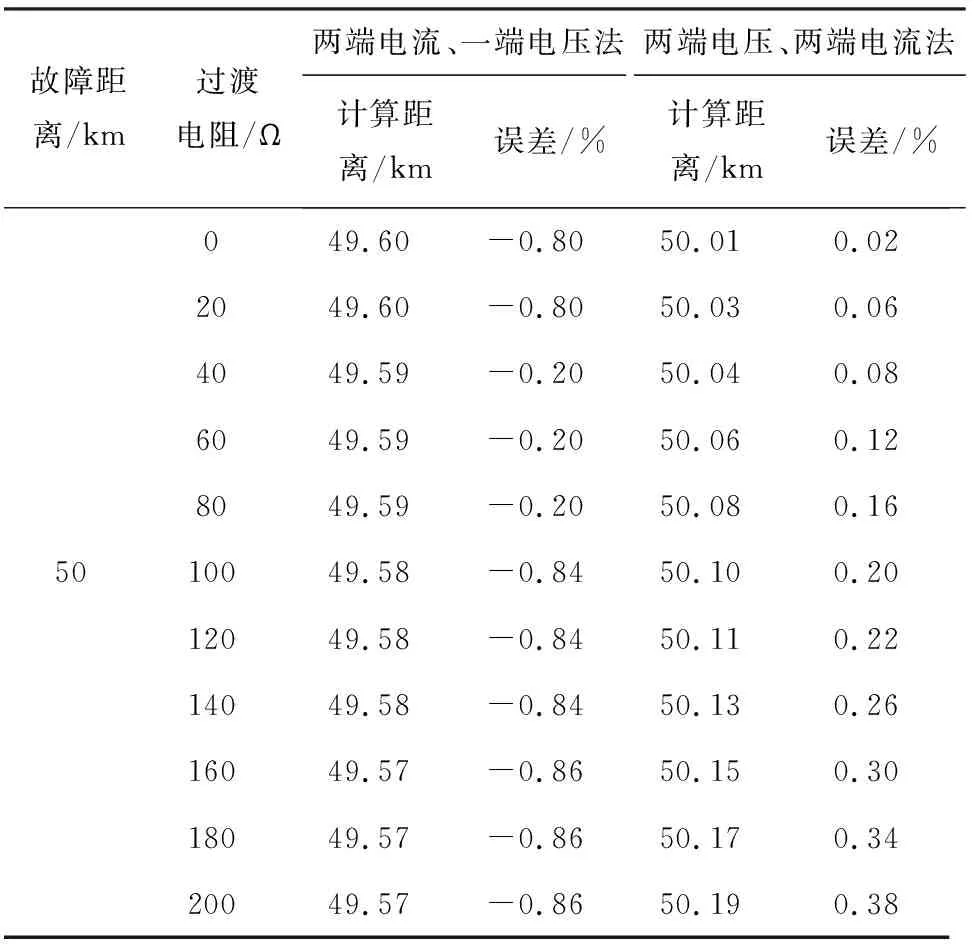
表3 故障发生在距m端50 km处的测距结果

4 结 语

对傅里叶滤波算法、单端和双端故障测距算法进行了理论推导和误差分析，并提出了相应的改进措施。

1)采用差分傅里叶算法来消除衰减直流分量对测距结果造成的误差，并配合模拟低通滤波器来消除差分傅里叶算法对高频分量幅值的放大作用。

2)在单端测距算法中将测量电抗值代替传统的测量阻抗值，证实了改进的电抗测距算法在低压单端供电系统中的有效性。

3)对双端测距算法中的两端电流、一端电压法和两端电流、两端电压法进行了理论推导和仿真分析，证实了两端电流、两端电压法的测距精度受故障电阻和故障距离等参数的影响较小。