安装误差对面齿轮承载传动性能的影响

彭先龙，徐琪超，侯祥颖，寇发荣

(1.西安科技大学 机械工程学院，陕西 西安 710054；2.南京航空航天大学 直升机传动技术重点实验室,江苏 南京 210016)

面齿轮传动是圆柱齿轮和锥齿轮组成的一种角度传动机构，目前主要应用于直升机主减速器、汽车差速器等重要的传动系统中[1]，其承载性能在一定程度上反映了齿轮平稳性、寿命等啮合品质指标。在面齿轮实际安装过程中，不可避免地存在安装误差[2]，使得面齿轮在传动过程中偏离理想安装位置，进而降低面齿轮的传动性能，因此研究安装误差对面齿轮承载传动性能的影响规律，可以为优化、提高其啮合品质提供理论依据。针对面齿轮传动性能分析的文献，主要集中于安装误差对各种修形齿面几何接触性能的定性影响[3- 4]，及其对承载性能的定性影响[5- 9]。因此，进一步探究安装误差对面齿轮承载传动性能的定量影响规律，以设计安装尺寸的公差范围。本文旨在以面齿轮传动为例，基于解析齿面建立面齿轮传动的有限元模型，对其承载接触问题进行求解，分析各种安装条件下的齿面接触应力、齿根弯曲应力、承载接触路径及承载传动误差(load tra-nsmission errors，LTE)，并初步确定了应力最大值、承载传动误差均值等指标与安装误差的函数关系。

1 含安装误差的面齿轮有限元模型

1.1 安装误差

根据文献[10]关于面齿轮传动啮合理论的阐述，可以建立小轮、面齿轮齿面方程并确定相关的几何参数。对齿面方程的求解，可获得齿面坐标，进而建立两轮啮合的三维模型，如图1所示。由于安装误差不可避免且现有研究表明安装误差对面齿轮几何传动性能有重要影响[11]，显然其对面齿轮承载传动性能的影响不可忽视。

图1 面齿轮传动安装误差示意Fig.1 Sketch of face gear drive misalignment

1.2 有限元模型的构建

通过数值计算获得小轮与面齿轮齿面的离散数据点，并将点阵绕轴线旋转获得轮齿节点[13]；按照ABAQUS中关于八节点六面体单元的编写规则，对轮齿网格模型的节点依次编号，并按顺序构建八节点单元；将上述生成的单齿网格模型绕轴线旋转，获得多个单齿模型，将其依次进行连接后得到多齿模型。由于面齿轮实际重合度大于2，为了确保计算结果的准确性，选择五齿模型。

图2为齿面接触分析(tooth contact analysis，TCA)输出的几何传动误差(transmission errors，TE)Δφ2。如图2所示，当考虑面齿轮传动的边缘接触时，其重合度大于2。图中第i(i=1,2,3…)条曲线是第i对齿的几何传动误差曲线，若视第3对齿为观测齿对，在该齿对进入啮合到退出啮合的过程中，三齿啮合区出现了3次，分别为φ3in～φ1out，φ4in～φ2out，φ5in～φ3out，两齿啮合区出现2次，分别为φ1out～φ4in，φ2out～φ5in。

图2 几何传动误差与两轮的转角Fig.2 Geometry transmission errors and rotation angle

鉴于上述分析并考虑到几何传动误差的表达式[14]，大轮转角φ2为：

φ2=((φ1-φ10)·N1)/N2+Δφ2

(1)

式中：φ1为TCA计算出的小轮转角；φ10为初始转角(且φ20=0)；N1、N2分别为小轮和面齿轮的齿数。

由图2与式(1)可知，若直接由TCA输出的转角装配两轮，则该转角必然大于或小于观测齿对前、后啮合齿对刚刚接触时的转角，并使有限元软件输出负变形的错误结果，因此应对上述不同啮合区域分别计算实际的几何传动误差和两轮的转角。

以无安装误差为例。在φ1out～φ4in的两齿啮合区内，齿对2的侧隙与观测齿对的侧隙有：δ3a≤δ2a；在φ2out～φ5in的两齿啮合区内，齿对4的侧隙与观测齿对的侧隙有：δ3b≤δ4b。因此在两齿啮合区，主要由观测齿对承载且观测齿对未产生边缘接触。

在φ3in～φ1out的三齿啮合区，齿对2、齿对1的侧隙和观测齿对的侧隙有：δ2<δ1且δ2<δ3，即此时主要由齿对2承载且齿对2未产生边缘接触；在φ4in～φ2out的三齿啮合区，齿对4、齿对2的侧隙和观测齿对的侧隙有：δ3<δ4且δ3<δ2，即此时主要由观测齿对承载且观测齿对未产生边缘接触，此情况与两齿啮合区的分析结果相同；在φ5in～φ3out的三齿啮合区，齿对5、齿对4的侧隙和观测齿对的侧隙有：δ4<δ5且δ4<δ3，即此时主要由齿对4承载且齿对4是齿面接触(非边缘接触)。

综上所述，判断完不同啮合区域的轮齿承载关系后，可通过下式确定观测齿对在有限元装配中实际的小轮转角φ1为：

φ1=φT1±nT1(T1=2π/N1，n=0,1,2,3,…)

(2)

几何传动误差Δφ2为：

Δφ2=Δφ2T(φT1±nT1)

(3)

大轮转角φ2为：

(4)

式中：φT1、φT2及Δφ2T分别为TCA计算出的观测齿对的小轮转角、大轮转角及几何传动误差。

当齿轮传动存在边缘接触时，进行有限元静力学分析时，都可通过判断不同啮合区域的轮齿承载关系，并利用TCA和式(2)～(4)，确定观测齿对啮入啮出过程中的转角(本算例TCA计算的步长为2π/(8N1)，从而修正齿轮副在有限元分析中的输入转角。本算例中，小轮输入扭矩为1 600 N·m且无安装误差时,修正前后获得的承载传动误差如图3所示。

图3 几何传动误差与修正前后的承载传动误差Fig.3 TE and LTE of before and after correction′s model

通过离散转角φ1、φ2分别将上述两轮五齿有限元模型变换(装配)到固定坐标系Sf中。对于面齿轮，在将其轮齿节点由自身坐标系变换到Sf的过程中(坐标变换过程可以参考文献[10])，建立包含安装误差的辅助坐标系，从而建立含安装误差的有限元模型，获得了两轮的五齿装配模型。利用Sf中两轮的五齿模型的节点、坐标及编号、单元编号及其节点编号等数据编写每一组转角下的inp文件，将这些inp文件导入ABAQUS，所得有限元模型如图4所示。该模型中，面齿轮、小轮(假想插齿刀)的齿数N2、N1(Ns)分别为160、25(28)；模数为6.35 mm；压力角为25°；轴夹角为90°；面齿轮内半径为480 mm，外半径为560 mm，小轮的齿宽与面齿轮齿宽均为80 mm；两轮网格密度(齿宽×齿高×齿厚)均为10×10×5，为获得较高的计算精度，下文算例模型中的网格密度皆为51×81×5，模型节点数为159 732，单元数为133 280。

图4 面齿轮传动的有限元模型Fig.4 Face gear drive finite element model

2 有限元前处理与后处理

2.1 有限元前处理

在有限元接触分析前，还需在inp文件中定义如下参数：1)两轮材料属性：密度为7 800 kg/m3，泊松比为0.29，弹性模量为206.8 GPa；2)单元属性：采用六面体一次缩减积分单元；3)接触:接触形式为面对面接触，设置面齿轮右侧齿面(主面)及与之啮合的小轮齿面(从面)为接触对，则五齿模型需建立五对接触面，接触属性为无摩擦硬接触；4)参考点:将小轮内圆柱面和两侧剖面与其轴线上任意参考点RP-1建立刚性约束；将面齿轮底面和两侧剖面与其轴线上任意参考点RP-2建立刚性约束(图4)；5)分析步:选用静力学通用算法，分析时长选择默认；6)输出变量:选择齿面接触应力、齿根弯曲应力、小轮转角位移量为场输出变量；7)边界条件及载荷:对面齿轮全约束，对小轮施加扭矩T并释放其绕轴线的旋转自由度，轻载时施加0.5 N·m的扭矩，满载时施加1 600 N·m的扭矩。

参考文献[15]中的有限元静态分析方法，通过编写基于Windows的批处理程序，将面齿轮啮入啮出过程中的全部inp文件批处理导入ABAQUS，进行承载接触问题的求解。

2.2 有限元结果及后处理

求解结束后，可得各啮合转角下的齿面接触应力、齿根弯曲应力、小轮参考点处的角位移Δφ1L等结果，面齿轮节锥面上的齿面接触应力云图及接触椭圆如图5所示。通过ABAQUS内嵌的python语言编写脚本文件，进行后处理[16]，可获得啮入啮出过程中的应力、小轮参考点的角位移等结果。

图5 齿面接触应力与接触椭圆Fig.5 Contact stress and contact ellipse of face gear

承载传动误差主要包括齿侧间隙、承载变形[17]，其中齿侧间隙可通过上述方法计算的几何传动误差Δφ2表示，承载变形则由上述后处理获得的小轮参考点的角位移Δφ1L表示，则承载传动误差为：

Δφ2L=Δφ2+(Δφ1L·N1)/N2

(5)

2.3 前处理设置准确性的检验

为验证计算结果的准确性，有必要对建模方法及前处理设置进行检验。计算结果显示本文算例单齿、多齿的齿面接触应力分别为864.43、784.11 MPa，两者相对赫兹接触应力计算结果的误差最大都不超过8%。本文算例与文献[18]中表3所示面齿轮参数及前处理条件相同，但本文算例齿宽缩短了8 mm。将本文算例的齿面接触应力和齿根弯曲应力与文献[18]的仿真结果进行对比，本文算例的齿面接触应力与齿根弯曲应力分别为1 620.31、88.46 MPa，两应力结果相对文献[18]仿真结果的误差皆小于7%。

轻载条件下，对准安装及Δγ=-0.05°时的承载传动误差如图2所示，承载传动误差曲线与几何传动误差曲线相互重合，说明在载荷接近于0时，不会产生接触变形和弯曲变形，所以承载传动误差与几何传动误差几乎相等。

应力对比及传动误差的对比结果说明了上述有限元建模方法及前处理设置的正确性。

3 有限元算例结果与分析

基于上述方法构建面齿轮传动有限元模型，求解各种安装条件下满载时面齿轮的承载接触问题，进而获得应力、齿面接触印痕、承载传动误差等信息。由TCA确定取值范围Δq为-0.3～0.3 mm，Δγ为-0.05～0.05°，ΔE为-0.5～0.5 mm。

为分析安装误差对面齿轮传动强度、平稳性的影响，须着重关注面齿轮应力最大值、承载传动误差均值随安装误差的变化情况。

3.1 安装误差对接触路径的影响

几何接触路径与承载接触路径如图6所示，当Δq、Δγ及ΔE分别取负值、正值时，几何接触路径与承载接触路径均分别向面齿轮内径、外径发生偏移。同时几何接触路径与承载接触路径对Δγ最敏感，因此为保证传动质量，在面齿轮的实际装配中应尽可能使Δγ趋于0。

图6 接触路径Fig.6 Contact trajectory

如图6所示，由于TCA通过切触方程确定可能的接触点，而有限元承载接触分析可以确定这些可能接触点是否承载，因此在轮齿更替时的啮入啮出点上，几何接触点与承载接触点的位置存在差异，反映啮入啮出点上两轮转角范围有一定差异。

3.2 安装误差对齿面接触应力的影响

正、负安装误差使面齿轮齿面接触应力、边缘接触应力有所减小或增大，如图7所示，当Δγ=-0.05°时，边缘接触应力最大值增加至2.26 GPa。

齿面接触应力最大值的增量ΔSc，

ΔSc=Scw-Sca

(6)

式中：Scw、Sca分别表示有、无安装误差时齿面接触应力的最大值。ΔSc随安装误差变化的规律如图8所示。

在安装误差作用下，ΔSc有增有减，如图8所示，总体上负值安装误差情况下ΔSc的变化幅度大于正值安装误差情况，且当Δγ=-0.05°时，ΔSc高达0.64 GPa，反映负值安装误差使面齿轮齿面接触强度有所降低。因此从提高面齿轮齿面接触强度的角度考虑，Δγ的下限尽可能取正值。

图7 安装误差对齿面接触应力的影响Fig.7 Influence of misalignment on contact stress

图8 安装误差对应力最大值的影响Fig.8 Influence of misalignment on maximum stress

3.3 安装误差对齿根弯曲应力的影响

安装误差对面齿轮齿根弯曲应力的影响规律如图9所示。各种安装条件下，当接触椭圆中心在节锥面附近时出现最大齿根弯曲应力，表明载荷主要由节锥面附近的齿面承受。

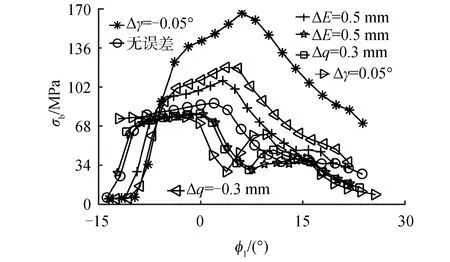
图9 安装误差对齿根弯曲应力的影响Fig.9 Influence of misalignment on bending stress

齿根弯曲应力最大值的增量ΔSb，

ΔSb=Sbw-Sba

(7)

式中：Sbw、Sba分别表示有、无安装误差时齿根弯曲应力的最大值。其随安装误差变化的规律如图8所示。

如图8所示，ΔSb随安装误差的变化基本呈减函数关系，且负值安装误差情况下ΔSb的变化幅度大于正值安装误差情况。当Δγ=-0.05°时，ΔSb达到了78.23 MPa，反映负值安装误差使面齿轮齿根弯曲强度有所降低。因此在考虑面齿轮齿根弯曲强度时，应着重关注负值Δγ。

3.4 安装误差对承载传动误差的影响

各种安装误差对承载传动误差的影响如图10所示，承载传动误差随着安装误差的增大整体向左偏移，反映安装误差导致啮入啮出过程中两轮的转角不同。安装误差对承载传动误差的幅值有明显影响。当ΔE=-0.5 mm、Δq=-0.2 mm和Δγ=-0.03°时，与无安装误差相比，承载传动误差幅值的最小值分别减小0.207″、0.13″和0.085″；当ΔE=0.3 mm、Δq=0.2 mm和Δγ=0.05°时，承载传动误差幅值的最大值分别增加0.339″、0.382″和0.825″。

如图10所示，安装误差对承载传动误差均值(图中平行于x轴的直线)也有明显影响。当ΔE=-0.5 mm、Δq=-0.3 mm和Δγ=-0.05°时，与无安装误差情况相比，承载传动误差的均值分别变化了1.148″、1.950″和5.963″；当ΔE=0.5 mm、Δq=0.3 mm和Δγ=0.05°时，承载传动误差的均值分别变化了0.746″、0.671″和0.164″。由于Δγ对承载传动误差的均值影响最大，从降低振动与冲击的方面考虑，在实际装配中应减少Δγ的公差范围。

承载传动误差均值的增量Δζ，

Δζ=ζS-ζP

(8)

式中：ζS、ζP分别表示有、无安装误差时承载传动误差的均值。

其随安装误差变化的曲线如图11所示。

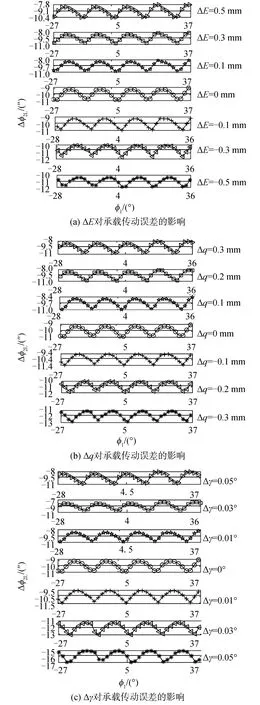
图10 安装误差对承载传动误差的影响Fig.10 Influence of misalignment on LTE

如图11所示，Δζ随安装误差的变化基本呈指数关系，Δζ随着Δq、Δγ及ΔE的增加而增大。

图11 安装误差对承载传动误差的影响Fig.11 Influence of misalignment on LTE

4 结论

1)本文面齿轮传动有限元建模基于齿面的解析坐标，模型装配基于坐标变换，该方法能够充分考虑齿面微观特征、微观安装误差对承载传动性能的影响。计算结果与经典方法的结果的比较，说明了本文建模及计算过程的正确性。

2)偏置安装误差、轴向安装误差和轴夹角安装误差均使接触、弯曲应力有所增加，但是这些安装误差取负值时将使得应力大幅增加。

3)承载传动误差幅值、均值随偏置安装误差、轴向安装误差和轴夹角安装误差的增大而增大，这些安装误差取负值时，承载传动误差的均值变化幅度大，反映轮齿啮合刚度有所减小。

4)从提高接触、弯曲强度和增加啮合刚度的角度来说，应该尽可能减少这些安装误差负值的绝对值，即这些偏差的下限最好不要超过0。