改进最小二乘法的非结构网格梯度重构算法
肖艺,明平剑
(哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001)
非结构网格有限体积法的梯度重构是计算流 体力学(computational fluid dynamics,CFD)的必要环节,其准确性和健壮性至关重要,是CFD研究的重点之一。由于非结构化网格高阶精度格式还存在诸多问题,目前应用最为广泛的方法仍然是具有二阶空间精度有限体积法。对于二阶空间精度的有限体积法,需要进行分片恒定梯度重构。对于高雷诺数的粘性流动模拟,通常会遇到大长宽比的弯曲网格,且边界层单元类型比较复杂,复合层材料导热中也会遇到此类网格。因此,非结构网格有限体积法的梯度重构仍然是有重要意义的研究课题。Diskin等[1]对非结构网格有限体积法梯度重构算法作了全面系统的归类,并且分析了各种梯度重构算法在二维大长宽比网格上的理论截断误差和数值收敛精度。Shim等[2]提出了格林-高斯加权的最小二乘梯度重构方法(weight least squares(green-gauss),WLSQ(G)),该方法的权函数的构造综合了距离反比加权最小二乘法(weight least squares,WLSQ)和格林-高斯法(green-gauss,G-G),并且考虑了单元中心之间的方位影响。Mishrik等[3]以二维四边形结构化网格为例,从理论上分析了格心型最小二乘法的截断误差与网格几何因素的相关性。张帆等[4]提出了基于格点的距离反比加权最小二乘梯度重构法(vertex-based weight least squares,VWLSQ(1)),即基于节点加权最小二乘梯度重构法。对于边界单元梯度重构,也有专门的研究[5-7]。
本文基于哈尔滨工程大学自主研发的大型通用输运方程数值分析软件通用数值计算平台,针对大长宽比弯曲网格,改进 WLSQ(G)得到了 BWLSQ(G)。
1 非结构网格有限体积法梯度重构
1.1 格心型有限体积法
格心型有限体积法的变量均储存在单元中心,考虑稳态热传导控制方程:
·(kT)=0
(1)
式中:k为导热系数;T为温度。对于格心型有限体积法,利用高斯公式在每个单元内积分为:
(2)

对于非结构化网格:
(3)
1.2 最小二乘法
假定相连单元中心之间的变量线性分布为:
φF=φC+φCr·(rF-rC)
(4)

(5)
方程(5)为超定方程,可通过解函数L的最小值求解:
(6)

方程组(5)还可通过正规化或格莱姆-施密特正交化[5]求解,文献[5]中指出,正规化法重构大长宽比的网格单元的梯度时会出现矩阵病态问题,进而导致梯度重构误差较大。本文中的最小二乘问题均通过求解式(6)最小值求解。
计算模板单元的选取是最小二乘法的核心问题,以图1中心单元为例,梯度重构的计算模板单元一般分为共面型模板(图1中的深色单元)和共点型模板(图1中的所有单元)。当网格质量较差时,引入更多单元的共点型模板能提高梯度重构精度,但也会导致计算量增加。对于二维的大长宽比网格,文献[1]中分析了WLSQ(n)法在共面单元模板和共点单元模板的理论截断误差,指出当计算模板单元最大距离比L=max{rCj}/min{rCj}与网格长宽比同量级时(见图2),WLSQ(n)能保持梯度重构精度;而当计算模板单元距离比的最大值远小于网格长单元比时,WLSQ(n)梯度重构精度下降。因此,计算模板单元的选取直接影响最小二乘法梯度重构的精度。

图1 最小二乘梯度重构单元模板Fig.1 Least squares gradient reconstruction stencil
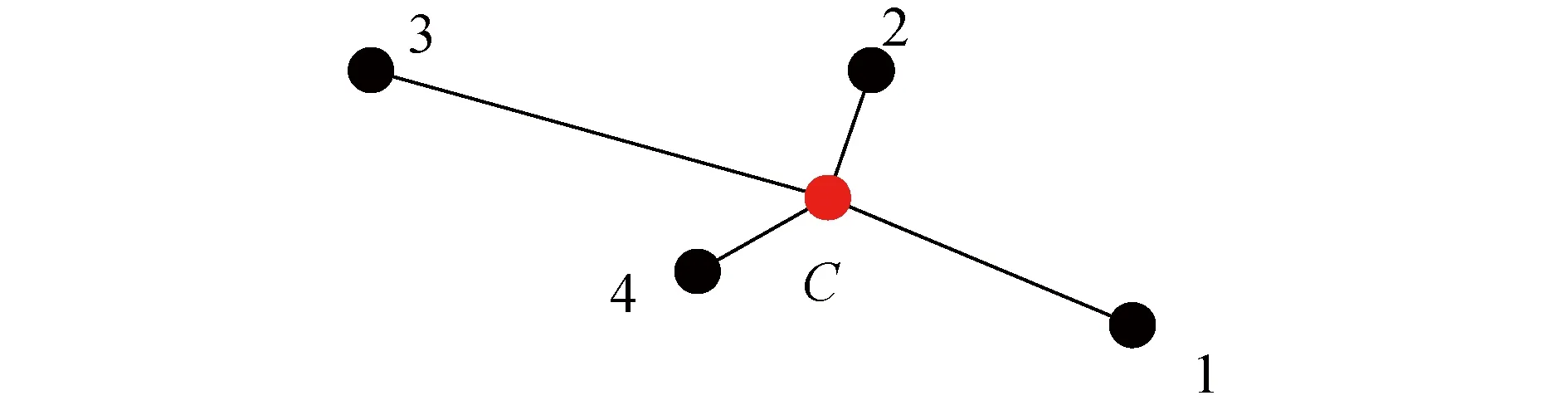
图2 插值模板单元最大距离比Fig.2 Maximum distance ratio of interpolation stencil
1.3 格林-高斯法
格林-高斯法是应用最广泛的空间梯度重构方法,由散度定理,单元中心变量空间梯度重构为:
(7)
式中:φfK为单元的第k个面的面心变量值;ΩC为单元的体积。
2 改进的加权最小二乘梯度重构
2.1 高斯加权最小二乘法
距离反比权重是加权的最小二乘法最常用的一种,但其与单元中心之间的方位无关。为了单元中心方位的影响,Shima[2]提出了高斯权重最小二乘法(WLSQ(G)),考虑格林-高斯法,式(6)可进一步改写为:
(8)
式中:αk为线性插值系数。考虑加权最小二乘法,求解式(6)最小值得:
(9)
式中:rck=rk-rc;Δrck和lck分別为单元C和相连单元k之间的距离和单位距离矢量。
对比式(8)和(9),在网格近似正交的情况下,可以认为nfk≈lck,仅考察单元k的权重,因此忽略常数系数1/Vo和M-1,可得:
ωk=αkSfk/Δrck=αWkSfk/Δrck
为在一维情况下达到二阶精度,取αWk为:

(10)
即高斯加权最小二乘法的权函数为:
(11)
式中:rc为单元C的格心坐标向量;rfk、nfk分为单元C的第k个面的面心坐标向量、外法线单位面积矢量;rk为单元C的第k个相连单元的格心坐标向量。WLSQ(G)法的最终形式为:
(12)
式中gi只与网格几何关系有关。图3为格林-高斯权重示意图。
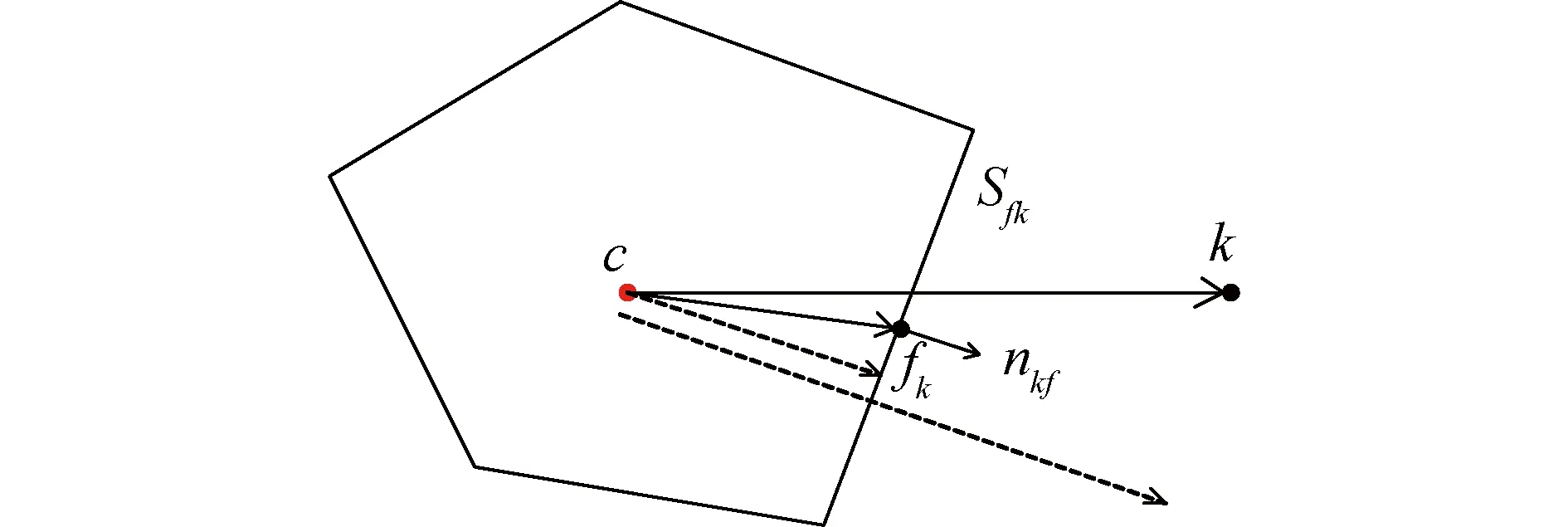
图3 格林-高斯权重示意Fig.3 Schematic of Green-Gauss weight
2.2 高斯加权最小二乘法理论截断误差分析
2.2.1 大长宽比弯曲四边形网格
考虑图4所示的大宽比弯曲四边形网格,网格在坐标(r,θ)的空间步长分别为hr和hθ,网格长宽为:
A=Rhq/hr>>1
(13)
网格的变形程度为:
(14)
图4中WLSQ(G)法重构单元O梯度的计算模板单元包括的N、S、W、E单元,以O为原点建立直角坐标系(e,n),各单元中心在坐标系(r,θ)和(n,e)的坐标如表1所示。

图4 大长宽比弯曲四边形网格示意Fig.4 Schematic of large aspect ratio curved quadrilateral mesh

表1 四边形网格模板单元中心在不同坐标系中的坐标值Table 1 Coordinate values of cell center of the stencil of quadrilateral mesh in different coordinate systems
在以O为原点的直角坐标系中,一般函数f(n,e)可由O、N、S、W、E共5个点通过线性最小二乘拟合。线性拟合函数fr(e,n)为:
fr(e,n)=fo+eeφ+nnφ
(15)
其中fo=f(0,0),eφ和nφ通过求解式(12)的得到。由式(11)计算各点的权重为:
ωN=ωS=2Rtan(hθ/2)/hr≈Rhθ/hr=A
(16)
ωW=ωE=hr/[2Rsin(hθ/2)]≈hr/Rhθ=1/A
(17)
解式(12)得:
(18)
故WLSQ(G)法对图2所示网格内部单元的梯度重构误差为Ο(hθ),为一阶收敛精度。
2.2.2 大长宽比弯曲三角形网格
将图4中的大宽比弯曲四边形网格划分为三角网格,如图5所示。图5中WLSQ(G)法重构单元O梯度的计算模板单元包括的1、2、3单元,以0为原点建立直角坐标系(e,n),各单元中心在坐标系(r,θ)和(n,e)的坐标如表2所示。

图5 大长宽比弯曲的三角形网格示意Fig.5 Schematic of large aspect ratio curved triangular mesh diagram

表2 三角形网格模板单元中心在不同坐标系中的坐标值Table 2 Coordinate values of cell center of the stencil of triangular mesh in different coordinate systems
由式(11)计算各点权重为:
ω1=ω2=3,ω3=3hr/(2Rhθ).
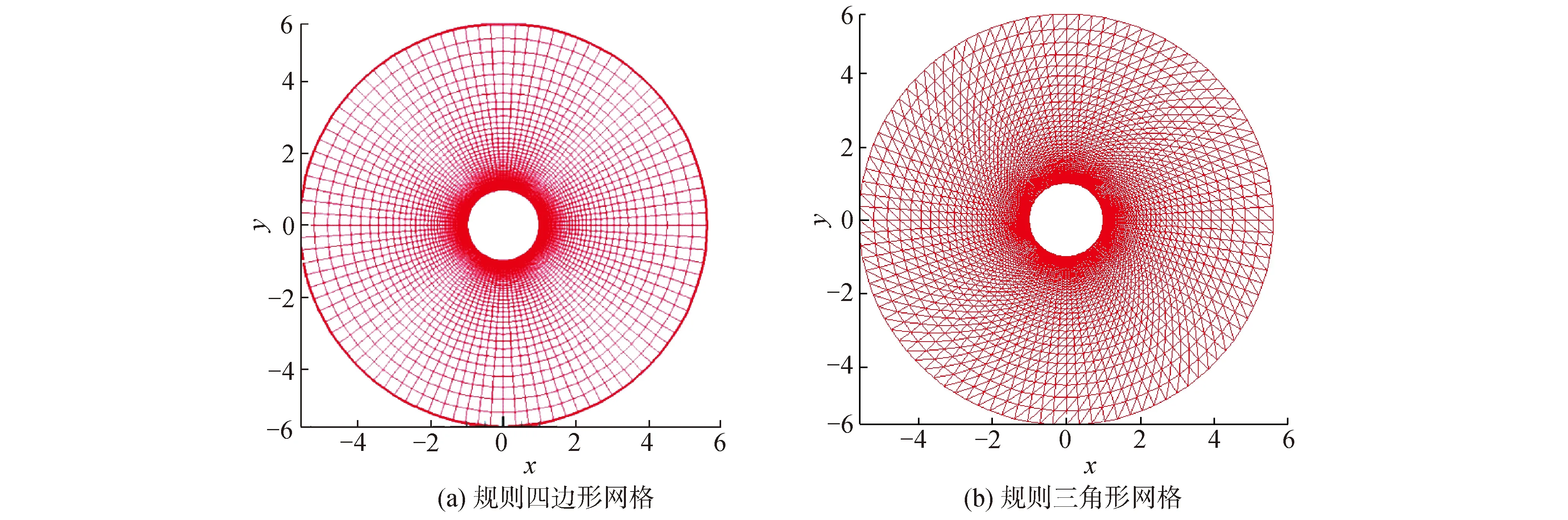
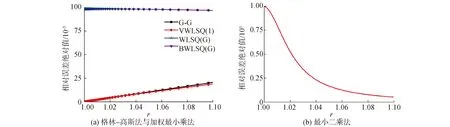
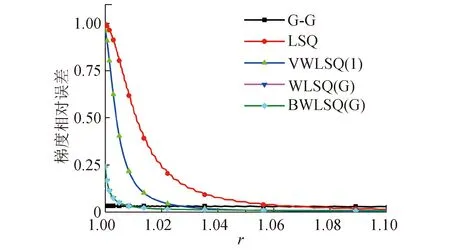
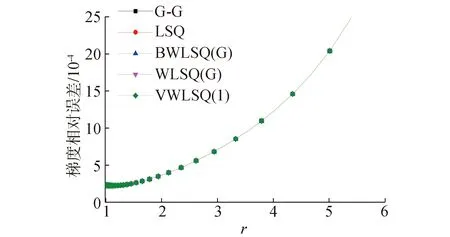
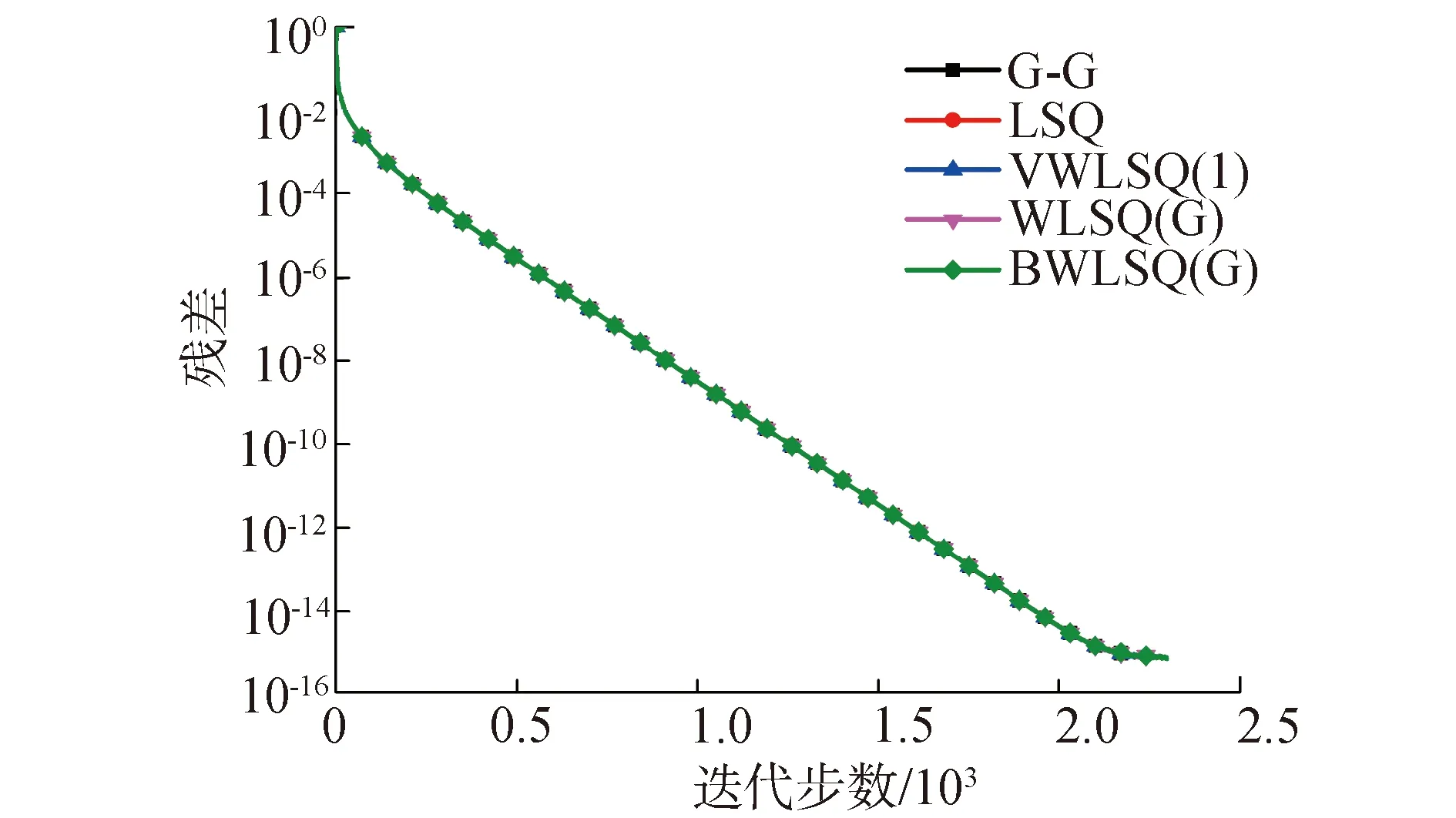
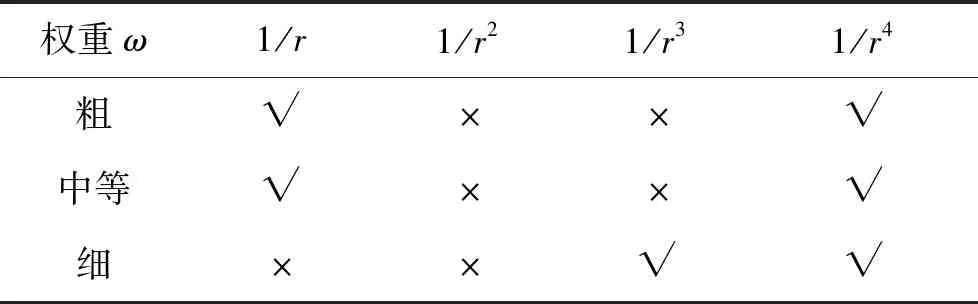
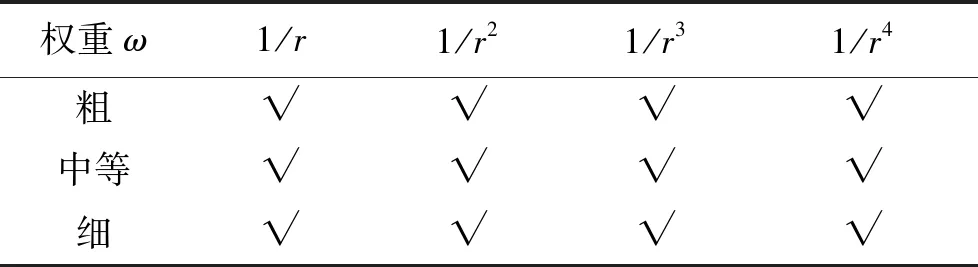
注意到Rhθ< (19) 故WLSQ(G)法对图5所示网格内部单元的梯度重构误差为ε=Ο(1),为零阶收敛精度。 2.2.3 矩形计算区域内部单元 考虑图6所示的大长宽比三角形网格,网格x和y方向的空间步长分别为hx和hy,网格长宽比A=hx/hy>>1。图4中,WLSQ(G)法重构单元O梯度的计算模板单元为1、2、3单元,以O为原点建立直角坐标系(x,y),各单元中心在坐标系(n,e)的坐标如表3所示。 由式(11)计算各点权重为: 式(12)得: (20) 图6 矩形域大长宽比三角形网格示意Fig.6 Schematic of large aspect ratio triangle mesh of rectangle domain 表3 模板单元中心在不同坐标系中的坐标值Table 3 Coordinate values of cell center of the stencil in different coordinate systems 故WLSQ(G)法对图6所示网格内部单元的梯度重构误差为Ο(hx),为一阶收敛精度。 对图7所示的大长宽比弯曲三角形网格边界单元O,WLSQ(G)法的计算模板单元由单元1、单元3、边界2组成。由2.2.2中对三角形网格分析可知,共面型计算模板L=Ο(1)< 图7 边界单元梯度重构模板Fig.7 Gradient reconstruction stencil of boundary element 考虑网格的弯曲、大长宽比,分别对WLSQ(G)、VWLSQ(1)、WLSQ(G)、G-G,LSQ法在图8所示的圆形域网格进行测试。采用了四边形网格和三角形网格,其中三角形网格是在四边形网格的基础上有序的按对角线剖分为2个三角形得到。为测试不同梯度重构方法在边界单元的数值收敛精度,按文献[2]中对图8所示的网格逐渐细化(分为别粗、中等、细3种网格尺寸),网格尺寸见表4。测试函数为f=r2=x2+y2,相对误差ε=|1-φ/(2r)|。 图8 圆环域网格示意(中等网格尺寸)Fig.8 Schematic of ring domain mesh(medium mesh size) 表4 网格尺寸Table 4 Mesh size 求解单层壁圆筒稳态导热问题,分别在粗、中等、细3种网格尺寸的三角形/四边形网格测试。本章以中等规格三角形/四边网格为例,分析不同梯度重构算法的计算结果。控制方程和边界条件为: (21) 式(20)的解析解为: T*=T1+(T2-T1)ln(r/r1)/ln(r2/r1) (22) 从图9(a)可看到,对于圆环形计算域四边形网格算例中的内部单元,G-G法和VWLSQ(1)法的计算结果相近,且比WLSQ(G)法误差整体小1个量级。G-G和VWLSQ(1)法的误差沿径向增大,而WLSQ(G)的误差沿径向减小。从图9(b)可看到,LSQ在1.0≤r≤1.1内的误差最大达到0.99。从图10可看到,对于边界单元,BWLSQ(G)、G-G、VWLSQ(1)的误差相近,均为一阶收敛精度;WLSQ(G)为二阶收敛精度,但其误差比BWLSQ(G)、G-G、VWLSQ(1)高2个量级;LSQ为零阶收敛精度。分析计算模板单元的几何关系,基于格心的最小二乘法的计算模板如图11所示,其格心梯度由其计算模板单元内插得到,且计算模板的最大距离比L=Ο(A),进而导致LSQ计算误差较大。 图9 圆环域四边形网格梯度重构误差分布Fig.9 Distribution of gradient reconstruction error of quadrilateral mesh in ring domain 从图12中可以看到,对于圆环域三角形网格内部单元,G-G法误差随径向增大,在1.0~1.1内,其误差为0.01~0.034,但其误差在r=1.1附近最大;BWLSQ(G)和WLSQ(G)计算结果相同,误差随径向减小;VWLSQ(1)法和LSQ法误差在r=1附近均大于0.90,且均随径向减小;在r=1处,WLSQ(G)和BWLSQ(G)最大误差为0.2,符合2.2.2节中理论截断误差分析得到的ε=Ο(1),主要由径向梯度误差导致。从图13中可知,对于边界单元,BWLSQ(G) 为一阶精度,其误差最小,且比WLSQ(G)误差小2个量级;G-G法误差次之,为一阶精度;WLSQ(G)为一阶精度,误差较大;LSQ和VWLSQ(1)均为零阶精度,且误差较大。分析计算模板单元的几何关系,基于格点的距离反比权重最小二乘法(VWLSQ(1))的计算模板单元如图14所示,当网格长宽比较大时,其格点梯度由外插值得到,且计算模板的最大距离比L≈2< 图10 圆环域四边形网格边界单元梯度重构误差Fig.10 Gradient reconstruction error of boundary element of quadrilateral mesh in ring domain 图11 大长宽比弯曲四边形网格基于格心的最小二乘模板Fig.11 Cell-centered least squares stencil of large aspect ratio curved quadrilateral mesh 图12 圆环域三角形网格梯度重构误差分布 Fig.12 Distribution of gradient reconstruction Error of triangle mesh in ring domain 对圆环稳态导热算例,从图15和图16可知在四边形网格上,VWLSQ、LSQ、GG、BWLSQ(G)、WLSQ(G)的误差和残差收敛速度相同。从图17可以看出,VWLSQ(1)整体误差最大,BWLSQ(G)和WLSQ(G)次之,G-G误差最小;在r=1处,VWLSQ(1)的误差要比G-G、BWLSQ(G)和WLSQ(G)高1个量级。从图18可以看出,LSQ计算发散;G-G和VWLSQ(1)残差衰减最快,BWLSQ(G)次之;当残差收敛时,BWLSQ(G)的所用迭代步数为WLSQ(G)的1/3,故针对三角形网格,BWLSQ(G)能有效的提高WLSQ(G)的计算效率。分析可知,对于四边形网格,BWLSQ(G)和WLSQ(G)的边界待求单元的计算模板均满足L=Ο(A),因此在四边形网格上的计算收敛性效率相同。对于三角形网格,WLSQ(G)的边界待求单元的计算模板为L=Ο(1)< 图13 圆环域三角形网格边界单元梯度重构误差Fig.13 Gradient reconstruction error of boundary elements of triangle mesh in ring domain 图14 大长宽比弯曲三角形网格基于格点的最小二乘模板Fig.14 Vertex-centered least squares stencil of large aspect ratio curved quadrilateral mesh 图15 圆环稳态导热四边形网格误差分布Fig.15 Error distribution of quadrilateral mesh of steady state heat conduction in ring domain 图16 圆环稳态导热误差四边形网格残差收敛Fig.16 Convergence of residual of steady state heat conduction in ring domain 图17 圆环稳态导热三角形网格误差分Fig.17 Error distribution of triangle mesh of steady state heat conduction inring domain 图18 圆环稳态导热三角形网格残差收敛Fig.18 Convergence of residual of triangle mesh of steady state heat conduction in ring domain 表5 BWLSQ(G)在圆环稳态导热三角形网格的计算结果Table 5 Calculation results of BWLSQ(G) of triangular mesh of steady-state heat conduction in the ring domain 表6 BWLSQ(G)在圆环稳态导热四边形网格的计算结果Table 6 Calculation results of BWLSQ(G) of quadrilateral mesh of steady-state heat conduction in the ring domain 1)对于大长宽比弯曲三角形/四边形网格,G-G法的计算结果要好于加权重的最小二乘法,且在边界单元为一阶收敛精度。 2)针对大长宽比弯曲三角形/四边形网格的边界单元,BWLSQ(G)法能有效减小边界单元梯度重构误差,达到一阶精度; 3)针对四边形网格,BWLSQ(G)计算效率与WLSQ(G)相同;针对三角形网格,BWLSQ(G)能有效提高WLSQ(G)的计算效率。 下一步工作需深入分析计算模板单元几何关系和权重对最小二乘插值系数矩阵的影响,并且应用于更复杂的实际问题中测试其适用性。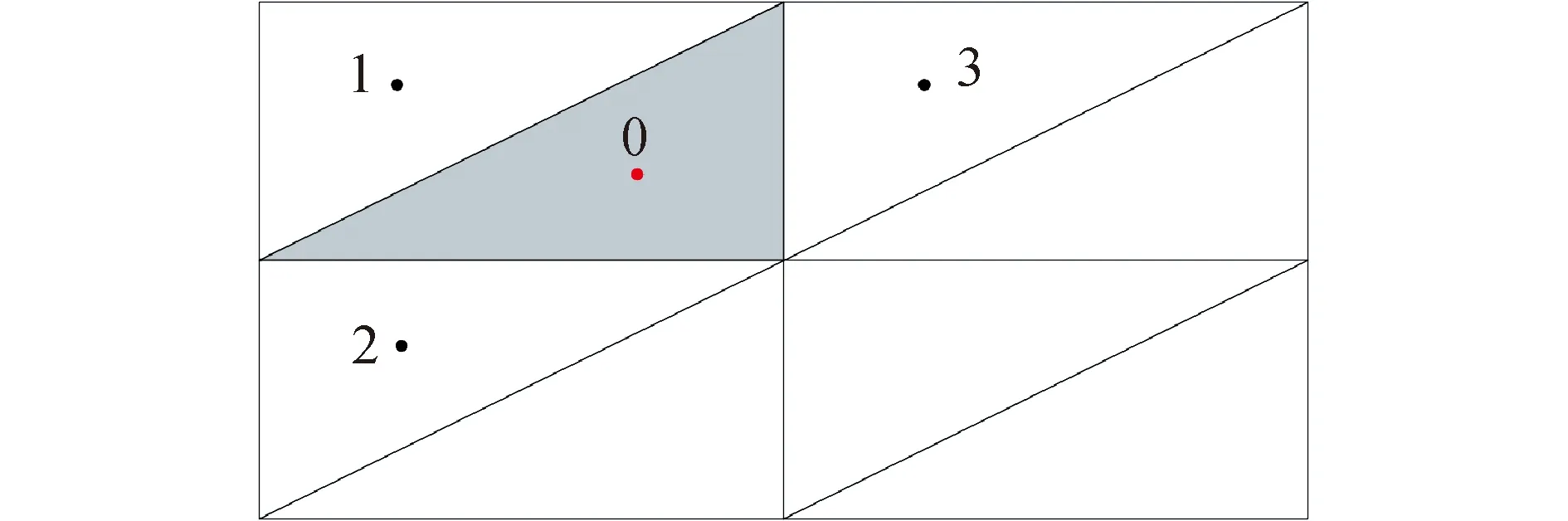

2.3 改进边界单元计算模板

3 数值算例与分析

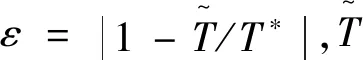






4 结论

