不确定环境下的Supply-hub协同补货决策

张令荣，崔春岳，李云风

(大连理工大学经济管理学院，辽宁 大连 116024)

1 引言

消费者需求的个性化、快速化、高频化与短周期，促使产品和技术不断更新换代，零部件供应商也处于不断创新之中。产品更新与需求的不确定性使得供应商选择趋于动态化。“互联网+”和大数据技术的应用，为供应商的动态变化提供强有力的技术支持。零部件创新与供应商选择的动态性，再加上生产、运输及订单处理过程中不确定性因素的影响，使得提前期不确定成为供应链补货决策中不可忽视的重要因素。

Supply-hub是为解决供应链上游协同补货问题发展起来的一种供应链协同运作模式。制造商委托Supply-hub第三方运营商管理零部件库存、JIT配送以及信息共享。基于Supply-hub的补货决策研究，Roshan和Viswanadham[1]研究了由两级供应商、Supply-hub和OEM制造商的供应链，以OEM制造商采购成本最小为目标，确定供应商的最佳生产和补货决策；Shah和Goh[2]研究了在由单供应商、Supply-hub和客户组成的需求确定的两级供应链中，以供应链总成本最低为目标，考虑库存惩罚成本因素，建立补货决策模型。但是以上研究都没有将Supply-hub视为信息共享中心，缺少Supply-hub协同补货决策研究，马士华等[3]考虑加工装配系统中的零部件滞存成本因素，提出了基于Supply-hub的供应商共享补货及库存信息的协同补货策略，发现能有效降低供应链系统成本以及供应商成本；马士华和吕飞[4]建立了需求随机情况下的基于Supply-hub的两供应商单制造商的生产与配送协同决策模型，证明协同决策会降低供应链总成本；关旭等[5]比较了需求不确定情况下VMI模式和Supply-hub模式在供应链响应性方面的区别，发现Supply-hub模式在响应性方面有优势；王建华和葛珍[6]将Supply-hub引入到下游供应链中，在两产品需求不确定情况下，建立了分别由制造商和零售商主导Supply-hub的生产批量模型。

对于提前期的研究，Ter[7]首先研究了提前期固定，需求服从泊松分布的(R,Q)策略下的补货决策模型；马士华等[3]研究了两供应商单制造商单产品提前期固定情况下，比较了供应商分散补货策略与供应商协同补货策略，发现协同策略优于分散补货策略；张云丰等[8]研究了需求和提前期均固定下的非瞬时补货改良品订购策略，发现联合采购可使订货批量成倍增加；全春光等[9]建立了在需求随机情况下的基于共同补货期的单制造商两分销商的协调补货模型，得出协调补货模型能够降低供应链期望运行成本；熊燕华和沈厚才[10]研究了提前期固定的按单装配系统中三供应商两产品的协同补货问题，对比分析了不同部件独立补货和协同补货两种策略，得出协同补货策略优于独立补货；张令荣等[11]研究了提前期固定需求不确定情况下复杂产品的三供应商两产品协同补货问题，得出协同补货策略优于独立补货策略；Li Guo等[12]建立了在需求固定和提前期为零时多供应商与多制造商的协同补货模型，得出协同决策优于分散决策。但是以上研究均为提前期固定情况下对补货决策的研究，Bookbinder和Cakanyildirin[13]研究了提前期随订货批量和安全库存量不同而变动情况下的连续盘点的库存模型，制定最优订货策略；桂华明[14]建立了单供应商单零售商单产品的需求不确定和提前期可通过成本增加减少的批量补货模型；叶峰涛等[15]研究了需求和提前期不确定下的企业内部订货与提前期决策问题；Braglia等[16]建立了在考虑随机需求和缺货成本条件下基于可控提前期的单供应商单制造商订货批量模型；周奇超等[17]建立了随机补货提前期下，两供应商对单制造商的准时供货模型，结果表明采用交货时间窗策略能有效降低供应商成本，通过调整延迟交货的惩罚成本，可以提高供应链协同水平；李群霞等[18]建立了单生产商多客户的提前订货库存模型，讨论了实现最小库存的提前期约束条件；李果等[19]考虑了交货时间的不确定性因素，建立了两供应商单制造商单产品的协同供货模型；Haibatolah等[20]研究了基于提前期不确定和需求周期变动的两级供应商单制造商的三级供应链的批量补货模型。

目前学者关于Supply-hub的协同补货研究以需求不确定性研究为主，将提前期假设为固定值，而在现实企业运行中，提前期不确定是企业补货决策中不得不考虑的因素。与两供应商单制造商的二级供应链相比，多供应商单制造商同时生产多种定制化产品是比较常见的现象，而定制化产品之间由于零部件的配套性，零部件补货也存在一定的关联性。基于此，本文研究了提前期随机和订单需求不确定情况下，考虑零部件配套性的三供应商单制造商生产两定制产品的Supply-hub协同补货决策。

2 问题描述及假设

某制造商生产P1和P2两种定制化产品，且两产品均按通用零部件与定制零部件数量比1∶1的进行组配(非1∶1关系可处理为1∶1)[11,19]，如图1。

图1 产品组配关系图

基于前人的研究[1,3-4,11]，提出基于Supply-hub的定制化产品供应链示意图，供应链中的制造商委托Supply-hub运营商管理零部件库存、JIT配送以及信息共享。制造商根据客户的定制化订单需求从供应商群中选择相应的零部件供应商，供应商S1、S2、S0是生产定制化产品所需零部件的供应商，代表着可以满足客户定制化需求与制造商要求的供应商，供应商的选择会根据订单不同处于动态变化之中。制造商将制定的生产计划及零部件需求信息等共享给Supply-hub运营商，再由Supply-hub运营商将库存及需求信息共享给供应商，最终由Supply-hub运营商或供应商制定补货策略。零部件送达Supply-hub后，Supply-hub运营商对其实施统一管理并按照制造商的需求将配套零部件直送制造商生产工位，供应商承担零部件的在Supply-hub期间的库存费用。产品生产完成后直接送至客户，不存在制成品库存。Supply-hub在该供应链运作中起到了信息共享平台和物料集成管理平台的作用，如图2所示。

为分析不同情形下供应商的最佳补货批量和供应链期望运行成本情况，作出以下假设：

假设1：产品P1和P2的订单总需求量是随机且独立的，均服从正态分布，产品P1和P2期望总需求量分别为D1和D2。

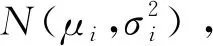
图2 基于Supply-hub的定制化产品供应链示意图

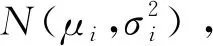
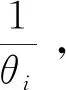
假设4：Supply-hub运营商采取连续检查库存策略，零部件按制造商生产计划成套配送到制造商工位，若一种零部件缺货，与之配套的零部件也不能被使用，产生滞存成本。由于就近设厂，配送时间很短，不会影响制造商生产。

假设6：制造商按定制化订单制定生产计划，生产多少就可以销售多少，不存在产成品库存。

假设8：供应商协同补货策略相对于独立补货策略，零部件协同补货管理成本为固定成本，由制造商承担。从整条供应链期望运行成本进行分析，不考虑制造商对供应商的惩罚成本等内部零和成本。

其他各项参数定义如下：

Fi：零部件Ci单位时间单次补货成本，包含每次订货的订货成本及运输成本

M：单位时间零部件协同补货管理固定成本，包含委托管理成本、直送工位成本等

hi：单位时间单位零部件Ci的库存持有成本

πi：单位时间内产品Pi缺货的单位惩罚成本

fi(xi):零部件Ci需求量xi的概率密度函数

gi(yi):零部件Ci的补货提前期yi概率密度函数

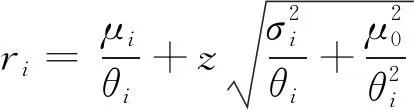
3 三种补货策略

3.1 基于分散决策的供应商独立补货策略

基于分散决策的供应商独立补货策略(简称DRP)下，在满足制造商要求的内部服务水平下，由各供应商进行补货批量、订货点等补货决策，即每个零部件供应商以自身运作成本最小化为目标，确定自己的最优补货批量。供应商库存水平变化如图3所示。

图3 DRP下供应商库存水平变化情况

(1)

零部件供应商S2的期望运作成本为：

(2)

零部件供应商S0的期望运作成本为:

(3)

制造商的期望运作成本：

(4)

供应链的期望成本为三供应商和制造商期望运行成本之和，即：

(5)

为方便计算，令：

(6)

3.2 基于Supply-hub的集中补货策略

基于Supply-hub的集中补货策略(简称JRP)，Supply-hub提供零部件库存管理、信息共享及直送工位服务，在满足制造商要求的内部服务水平下，Supply-hub运营商根据需求与库存信息，以供应链整体期望运行成本最小化为目标，确定各供应商的最优补货批量。

供应链的期望运作成本为：

(D1+D2)c2+M

(7)

证明：当Qi>0，E(TC)JRP自变量定义域内连续且二阶可导,Q0、Q1、Q2相互独立，具体证明过程见文献[11]。

在JRP下，最优补货批量为

E(TC)JRP=

(8)

3.3 基于Supply-hub的批量和时间协同补货策略

基于Supply-hub的批量和时间协同补货策略(简称CRP)，由Supply-hub进行供应链的补货决策，以供应链的期望运行成本最小化为目标，零部件补货计划在共同的补货周期内同时到货，又同时消耗完。两种产品均使用通用件，因此以通用件的库存水平作为批量及时间协同的关键考量。

图4 CRP下Supply-hub中库存水平变化情况

供应链的期望运行成本为：

(9)

为方便计算，令：

f1(x1)dx1,

f2(x2)dx2,

A=F0+(h0+π1)(δ-α)a2+(h0+π2)(ε-β)b2,

B=F1+(h0+π1)a2α,C=F2+(h0+π2)b2β,

则

+h1D1a1+h2D2b1+h0(D1+D2)c1

+(h0+π1)D1a2+(h0+π2)D2b2

(10)

证明：分别求式(10)关于m、n的偏导，并令一阶导数为零，可得：

(11)

(12)

将m*,n*代入式(10)，并求Q的一阶导数，并令一阶导数为零，可得：

(13)

将式(13)代入(11)、(12)，可得：

为证明式(13)、(14)和(15)为最优解，构建海瑟矩阵：

H(Q*,m*,n*)

一阶顺序主子式为：

二阶顺序主子式为：

三阶顺序主子式为：

定理4A>0,JRP下的供应链期望运行成本恒大于CRP下的供应链期望运行成本。

证明：

同时平方然后相减可得：2h0(D1+D2)(F0-A)=-2h0(D1+D2)[(h0+π1)(δ-α)a2+(h0+π2)(ε-β)b2]

∵δ<α,ε<β

∴-2h0(D1+D2)[(h0+π1)(δ-α)a2+(h0+π2)(ε-β)b2]>0

∴E(TC)JRP-E(TC)CRP>0

即JRP下供应链期望运行成本恒大于CRP下供应链期望运行成本。

4 算例分析

4.1 供应商服务水平变化对供应链期望运作成本的影响

为探究供应商服务水平变化对供应链期望运作成本的影响，分别计算了供应商服务水平在91%～96%之间11个不同水平下的供应链期望运行成本。

由图5可知，三种策略的供应链运作期望运行成本随着服务水平的提升而呈现U型分布,无论服务水平如何变化，JRP下的期望运行成本恒大于CRP下的期望运行成本。三种策略均存在最优的供应商服务水平使得供应链期望运作成本最小。当供应商服务水平低于94.5%时，CRP策略有成本优势；当超过94.5%时，DRP相对有成本优势。当供应商的服务水平很高时，缺货、延迟到货等情况几乎不发生，供应链补货不需要专门的Supply-hub进行协同补货就已经实现了高水平的协同。服务水平并不是越高越好，而是要控制在合理范围之内。

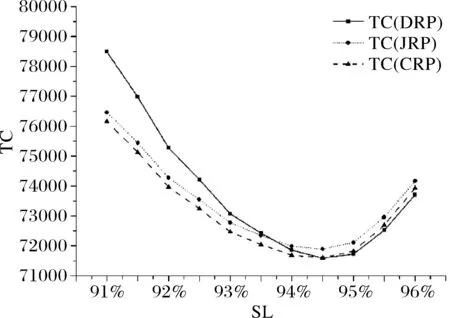
图5 不同服务水平下供应链的成本变化曲线

4.2 需求波动对供应链期望运作成本的影响

为探讨需求波动对供应链期望运作成本的影响，计算需求波动即标准差分别在(2,3,3.61)，(3,4,5)，(4,5,6.40)，(5,6,7.81)，(6,7,9.22)，(7,8,10.63)，(8,9,12.04)，(9,10,13.45)，(10,11,14.87)下，三种策略的供应链期望运行成本的变动情况。

由图6可知，无论需求标准差如何变化，JRP下的期望运行成本恒大于CRP下的期望运行成本。随着需求波动的加剧，供应链期望运行成本也在不断升高，应对需求波动变化增加了供应链期望运行成本。随着需求波动的加剧，CRP相对JRP的成本优势呈现出倒U型分布。在需求波动小时，DRP的期望运行成本要小于CRP与JRP的期望运行成本；随着需求波动的增加，DRP的成本逐渐高于CRP的成本，并且超过了JRP下的期望运行成本。随着需求的不确定性增加，供应商协同补货策略相对于供应商独立补货决策的成本优势将会越来越明显。

图6 不同需求标准差下供应链期望运行成本变化曲线

4.3 提前期波动对供应链期望运作成本的影响

为探讨提前期波动对供应链期望运作成本的影响，计算零部件C0的补货提前期分别服从参数为8,9,10,12,13,14的指数分布，定制件C1的补货提前期分别服从参数为4.5,5,5.5,6,6.5,7,7.5的指数分布，零部件C2的补货提前期分别服从参数为6.5,7,7.5,8,8.5,9,9.5的指数分布，三种策略的供应链期望运行成本的变动情况。

由图7-图9可知，无论通用件和定制件的提前期参数如何变动，JRP下的期望运行成本恒大于CRP下的期望运行成本。随着提前期期望值和不确定性的增加，供应链期望运行成本呈现先减后增的U型分布，说明存在最优的补货提前期期望值使得成本最小。不同的零部件的最优提前期不同，通用件的最优提前期要明显大于定制件的最优提前期。通用件的提前期变动对供应链期望运行成本的影响要大于定制件的影响。

图7 通用件C0的提前期波动时供应链期望运行成本变化曲线

图8 定制件C1的提前期波动时供应链期望运行成本变化曲线

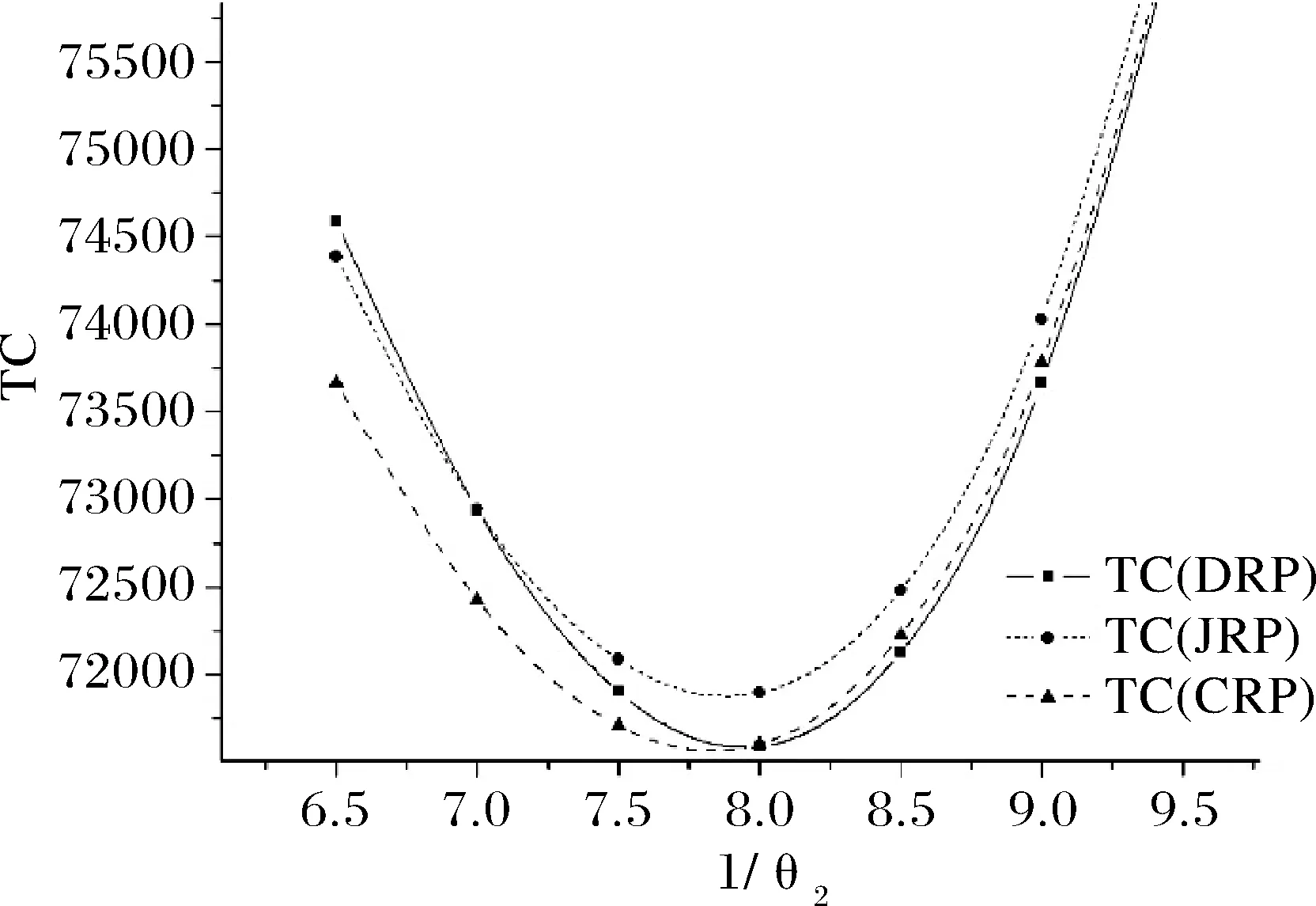
图9 定制件C2的提前期波动时供应链期望运行成本变化曲线

4.4 其它参数变化对供应链期望运行成本的影响

由前文的讨论可知，供应链期望运行成本包括补货成本、库存成本、滞存成本和缺货成本在供应链期望运行成本，因此分别对单次补货成本、单位库存成本和单位缺货成本相关参数进行讨论，以产品P1为例，探讨F0∈(50,350)，步长为50；F1∈(50,350)，步长为50；h0∈(5,11)，步长为1；h1∈(5,17)，步长为2；π1∈(30,60)，步长为5，供应链期望运行成本的变化情况如图11-14所示。

综上五个影响成本参数的算例，随着参数F0、F1、h0、h1、π1的增加，供应链运行期望运行成本在增加，但无论参数如何变动，JRP下的期望运行成本恒大于CRP下的期望运行成本。随着库存成本和惩罚成本的增加，最优策略由DRP变为CRP策略。补货成本越高，DRP策略优势越大；而库存成本和惩罚成本越高，CRP策略优势越大。单位库存成本的影响要大于单位惩罚成本的影响。

5 结语

本文主要是针对不确定环境下即提前期不确定

图10 F0变化对供应链期望运行成本的影响

图11 F1变化对供应链期望运行成本的影响

图12 h0变化对供应链期望运行成本的影响

图13 h1变化对供应链期望运行成本的影响

图14 π1变化对供应链期望运行成本的影响

和需求不确定，考虑零部件配套性的三供应商单制造商生产两种定制产品，分别对基于分散决策的供应商独立补货策略、基于Supply-hub的集中补货策略、基于Supply-hub的批量及时间协同的补货策略，进行求解和算例验证，得出如下结论：

(1)三种补货策略均存在唯一最优补货批量，使得供应链期望运行成本最小。基于Supply-hub的两种补货策略和基于分散决策的供应商独立补货策略各有优势，但基于Supply-hub的批量及时间协同的补货策略恒优于基于Supply-hub的集中补货策略。因此，在Supply-hub补货模式下，应努力实现供应商补货的时间及批量协同。

(2)三种补货策略的期望运行成本均随着供应商服务水平的变化呈U型分布，存在唯一最优的服务水平，当供应商达到一定服务水平水平时，基于Supply-hub的批量及时间协同的补货策略最优；当服务水平过高时，基于分散决策的供应商独立补货策略最优。企业在选择补货策略时，要考虑供应商服务水平的因素，供应商服务水平并非越高越好，应在合理范围之内。

(3)随着需求波动的加剧，三种补货策略的期望运行成本均在增加，在需求波动小时，供应商独立补货策略有优势；在需求波动大时，基于Supply-hub的批量及时间协同的补货策略有优势，说明基于Supply-hub的批量及时间协同的补货策略能有效降低需求不确定性带来的成本增加风险。

(4)在提前期波动时，三种策略的供应链期望运行成本呈现U型分布。通用件的提前期波动对于供应链期望运行成本的影响要高于定制件提前期波动的影响，通用件的最优提前期要大于定制件最优提前期。因此企业应更加关注通用件提前期波动的影响，控制定制件提前期在尽可能靠近最优提前期的同时小于通用件提前期。