基于合作博弈模型的公共河流水资源分配方案研究
王先甲,刘 佳
(1.武汉大学经济与管理学院,湖北 武汉 430072;2.武汉大学系统工程研究所,湖北 武汉 430072)
1 引言
人类社会的高速发展使得水资源的使用与消耗速度逐步增加,此外河流、湖泊、地下水的污染使得可用的水资源逐步减少,水资源的稀缺性日益突出。流域中各地区受其经济环境和地理位置等因素的影响,水资源产生的效用也各不相同。如何合理地分配水资源成为水资源管理的重要问题。
公共河流是指流经不同行政地区的河流[1-2]。受地形环境、政治等因素的影响,公共河流流经的各用水主体之间充满了冲突与矛盾[3-4],研究公共河流的水资源分配问题有着重要的现实意义[4]。例如黄河自西向东流经中国9个省,长江干流流经中国11个省、自治区、直辖市。在流经省市之间合理地分配黄河和长江的水资源影响着整个黄河和长江地区人们的生产、生活。可以说,公共河流中的水资源分配结果影响整个地区的经济、政治活动。
根据水流的流向,公共河流的用水主体具有上下游关系。河流下游用水主体的用水策略受到上游用水主体用水策略的影响,上下游之间的用水存在冲突与矛盾,优化理论和博弈论是处理这种冲突问题的有力工具。以往水资源分配问题的研究主要集中在各用水主体之间关于水资源分配的竞争问题或者合作问题上。分析竞争问题时,以最大化产生的经济效用、环境收益等为目标,建立优化模型或者博弈模型,进而依据优化理论与博弈论得到水资源分配的优化策略[5-10],如Madani[5]对使用一系列非合作博弈模型来解决水资源管理和冲突中的问题进行了综述;刘文强等[6]使用博弈论对流域水分配问题中用水冲突矛盾进行揭示和解释;肖志娟等[7]应用博弈论原理与方法求解应急调水的合理补偿量问题,解决调水各方的利益冲突;魏守科等[8]运用非合作与合作博弈的方法,对南水北调中线工程水资源管理中的有关利益冲突进行模拟和分析。Ahmad等[9]使用两层多目标模型来研究水库管理者与用水部门之间的水资源分配问题;Fu Yicheng等[10]从可持续发展的角度出发,使用多目标优化模型来分析考虑社会公平等条件影响下的水资源分配方案。这些模型使得各用水主体的目标达到最优,并体现他们之间通过竞争来分配水资源的过程。而分析合作问题时,一般以合作博弈理论为基础,研究各用水主体对水资源进行统一分配时的合理分配结果[11-18],如付湘等[11]采用合作博弈方法建立水资源用户合作博弈模型, 使得使用合作博弈分配方式的总效益大于使用非合作博弈方法分配的总效益;张乐等[12]对突发水灾害应急管理中的多主体合作问题进行了探讨;Wang等[13]考虑水权和水资源转移对水资源分配结果的影响;Parrachino等[14]综述了合作博弈理论在水资源问题上的应用;Ni Debing和Wang Yuntong[15]、Avarideh等[16]从国际法律对分配的约束的角度出发,使用合作博弈理论研究污染河流治污成本的分摊问题;Xiao等[17]在一个综合的合作水分配框架内研究了水需求管理方案对水系统及其用户的影响;Degefu等[18]使用Nash协商的方式来研究稀缺性的水资源分配问题。这些合作博弈模型体现了各用水主体通过合作方式来分配水资源的过程。现实的水资源分配问题中,各用水主体之间可能既存在竞争,又存在合作。目前,水资源分配问题的研究忽略了各用水主体之间的竞争与合作并存的现象,从而导致现有模型只能从一方面,即竞争方面或者合作方面,来研究水资源分配问题,无法综合考虑用水主体之间竞争与合作并存时的水资源分配问题。
公共河流的水资源分配问题中,各用水主体之间可以根据经济、政治、地理环境等因素组成相应的联盟,从而加强自身竞争能力,这种形成联盟的行为体现各用水主体之间的合作行为。联盟之间通过竞争的方式来分配公共河流的水资源,这种水资源分配方式体现了各用水主体之间的竞争行为。因此,如何描述这种联盟之间竞争、联盟之内合作的行为,提出相应的最优分配方案并确定各用水主体之间联盟的具体形式,为合理使用公共河流的水资源提供了相应的理论依据和方法指导。
受外部性影响,参与者之间可以形成联盟来进行博弈,并且联盟的收益不仅与联盟自身有关,而且与联盟之外参与者的联盟结构有关。传统合作博弈理论假设联盟的收益仅与联盟自身有关,而与联盟之外其他参与者的联盟结构无关。因此,无法使用传统的合作博弈模型来直接描述外部性环境中的水资源分配问题。本文建立具有外部性的合作博弈模型来分析公共河流的水资源分配问题,研究联盟之间竞争、联盟之内合作这种竞争与合作并存时各用水主体之间的最优水资源分配方案,解决了现有优化或者博弈模型中分别讨论竞争或者合作行为的不足,得到了使得水资源分配的合理方案和参与者之间形成联盟的具体形式。
2 博弈模型分析
为了描述公共河流沿线的各用水主体之间在联盟之内合作、联盟之间竞争这种现象,分析各用水主体之间同时存在竞争与合作行为时对水资源分配结果产生的影响,首先本文给出具有外部性的合作博弈模型,然后在联盟之间通过动态博弈的方式来确定联盟的均衡水资源分配量,在联盟之内各参与者之间通过Nash协商的方式分配联盟的均衡水资源分配量。比较各种方案下用水主体产生的总效用,进而得到公共河流用水主体之间竞争与合作并存时最优的水资源分配方案和其形成联盟的具体形式。
2.1 具有外部性的合作博弈模型
一条河流流经多个国家、省市或者地区,这些国家、省市或者地区称为是各用水主体。所有用水主体组成的集合记为N={1,2,…,n},且|n|≥2。不失一般性,假设用水主体按顺序从上游到下游排列,即∀i,j∈N且i 假设用水主体形成m+1个联盟,本文使用集合N的一个划分,如下P={[1,s1],[s1+1,s2],…,[sm-1+1,sm],[sm+1,n]}表示用水主体之间形成联盟的形式,即为联盟结构。所有联盟结构组成的集合记为。用水主体之间为了得到更多的水资源量而形成联盟。形成联盟后,由于下游联盟受到上游联盟结盟行为的影响,这种联盟的效用受到联盟之外用水主体结盟行为的影响称为外部性影响。此时需要描述具有外部性环境影响下各用水主体形成联盟的效用。本文使用函数π描述此时联盟的效用。其中对于表示联盟结构P中的联盟[i,j]分配x单位的水资源产生的效用,即它是关于联盟分配的用水量的函数。 本文使用的具有外部性的合作博弈模型记为(N,,其中N为用水主体集合,为所有联盟结构组成的集合,ui为用水主体i分配用水量的效用函数,为联盟结构P中联盟[i,j]的效用函数,q为公共河流的总来水量。用水主体之间可以形成联盟[i,j],其中i,j∈N且i≤j。联盟之间通过竞争的方式来分配公共河流的总来水量q,由于河流具有流向,联盟之间具有上下游的关系,此时联盟之间通过Stackelberg模型分配总来水量q。各联盟按照这种分配方式分得河流的总来水量之后,各联盟内部通过协商的方式分配联盟的均衡水资源分配量。本文采用Nash协商模型在每一个联盟中分配联盟的均衡水资源分配量。 例1:外部性环境对联盟的均衡水资源分配量的影响。 一条公共河流流经四个不同的地区,从上游到下游按顺序记为1,2,3,4,所有用水主体组成的集合记为N={1,2,3,4}。四个用水主体形成的联盟结构为:{{1},{2},{3},{4}}、{{1},[2,3],{4}}、{{1},{2},[3,4]}、{{1},[2,4]}、{[1,2],{3},{4}}、{[1,2],[3,4]}、{[1,3],{4}}和{[1,4]}。 这里以联盟[1,2]的收益为例来说明外部性环境的影响。假设在联盟结构{[1,2],{3},{4}}中,联盟[1,2]分配的均衡水资源分配量为15;在联盟结构{[1,2],[3,4]}中,联盟[1,2]分配的均衡水资源分配量为10。受到外部性环境的影响,联盟[1,2]的收益受到其他参与者3和4的联盟结构的影响。从联盟[1,2]的角度出发,为了得到尽可能多的水资源,联盟[1,2]希望参与者3和4形成{{3},{4}}的联盟结构,进而形成联盟结构{[1,2],{3},{4}}并得到15个单位的水资源。 用水主体之间通过竞争的方式来确定联盟的收益。受到水流流向的限制,用水主体之间存在上游或者下游的关系。因此,上游用水主体的用水策略会影响下游用水主体的决策,此类问题可以使用动态博弈的方法来处理。该问题实际上是一个上游用水主体主导的Stackelberg寡头竞争问题。 (1) s.t.W[1,s1](yP)≥0 (2) s.t.W[s1+1,s2](yP)≥0 (3) s.t.W[sm+1,n](yP)≥0 其中W[sm+1,n](yP)≥0为最下游联盟[sm+1,n]的水文约束。 求解此类动态博弈问题的方法为逆向归纳法。从最后一个优化问题出发,求解最下游联盟[sm+1,n]使用的最优用水量与所有上游联盟用水量之间的关系,即求解出其最优反应。然后代入上一联盟[sm-1+1,sm]的优化问题,求解出联盟[sm-1+1,sm]的最优用水量与其所有上游联盟用水量之间的关系,继续这个过程,直到求解出第一个联盟的最优用水量为止。此时可以得到这个多阶段动态博弈问题的均衡解,进而可以确定联盟之间通过竞争方式分配的均衡水资源分配量方案。 为了说明外部性对联盟的效用之和的影响,首先介绍如下引理。 引理1:具有外部性的合作博弈中,若其满足凸性,则全联盟是联盟的效用之和最大的联盟结构。即对∀P∈,有 (4) 证明:这个结论为文献[19]的推论1。 这里需要说明的是,联盟满足凸性是指联盟的均衡水资源分配效用函数v(S,P)满足凸性。若对任意的联盟S,T⊆N,S∩T=∅,PN-(S∪T)为N-(S∪T)的一个联盟结构,有 v(S∪T,{S∪T}∪PN-(S∪T))+v(S∩T,{S∩T,S-T,T-S}∪PN-(S∪T))≥v(S,{S,T-S}∪PN-(S∪T))+v(T,{T,S-T}∪PN-(S∪T)) (5) 凸性是比超可加性更加弱的条件,由引理1可知,全联盟在博弈满足凸性时是联盟的效用之和最大的联盟结构。 相较于凸性,我们有凹性的定义。假设联盟的均衡水资源分配效用函数v(S,P)满足凹性,即对任意的联盟S,T⊆N,S∩T=∅,PN-(S∪T)为N-(S∪T)的一个联盟结构,有如下不等式成立 v(S∪T,{S∪T}∪PN-(S∪T))+v(S∩T,{S∩T,S-T,T-S}∪PN-(S∪T))≤v(S,{S,T-S}∪PN-(S∪T))+v(T,{T,S-T}∪PN-(S∪T)) (6) (5)式((6)式)的大于等于(小于等于)符号变为大于(小于)时,则称合作博弈满足强凸性(强凹性)。 相比于引理1,有引理2。 引理2:具有外部性的合作博弈中,若其满足凹性,则单点集合构成的联盟结构是联盟的效用之和最大的联盟结构。即对∀P∈,有 (7) 证明:这个结论为文献[20]的引理4。 证明:这一结论可以由文献[20]中的推论1和推论3得到。 引理3说明了一般情况下,参与者之间形成联盟的效用之和最大的联盟结构的位置。通过引理2可以得到如下命题。 证明:依据引理3可以得到命题1的结论。 另外,我们在这里举一个反例来说明全联盟不是联盟效用之和最大的联盟结构的情况,假设在具有外部性的合作博弈中,均衡水资源分配效用函数v满足强凹性,则由引理2知,单点集合构成的联盟结构是唯一联盟的效用之和最大的联盟结构。因此,单点集合构成的联盟的效用之和大于全联盟的联盟效用。 在传统的合作博弈模型中,一般假设特征函数满足超可加性,此时导致了全联盟{{N}}的总效用是最大的。而在具有外部性合作博弈中,一般不对联盟的均衡水资源分配效用函数,即特征函数,做过多的假设,这是导致命题1成立的根本原因。若假设具有外部性的合作博弈中,联盟的均衡水资源分配效用函数同样满足超可加性或者凸性,依据引理1可知,全联盟的联盟总效用之和是最大的,这与传统合作博弈的结果相同。 例2:通过动态博弈Stackelberg模型来确定联盟的均衡水资源分配向量。 (8) (9) 使目标函数一阶导数为零,求解得到上游联盟[1,2]的均衡资源分配量为: 本文中,博弈的参与者为用水主体,他们之间形成联盟并在任意联盟内部的参与者之间通过Nash协商的方式分配联盟的均衡资源分配量。假设联盟[i,j]中的任意用水主体k∈[i,j]的效用函数为uk,联盟结构P中任意联盟[i,j]之内的用水主体通过Nash协商方式来分配联盟的均衡水资源分配量。根据Nash协商定理[21]可知,联盟结构P中任意联盟[i,j]中的用水主体通过Nash协商的方式分配水资源的结果等价于如下优化问题的解 (10) G(xi,xi+1,…,xj)≥0 其中,G(xi,xi+1,…,xj)≥0为联盟[i,j]分配水资源向量(xi,xi+1,…,xj)时满足的水文约束。联盟之内的用水主体通过Nash协商的方式分配联盟的均衡水资源分配量的方法模拟了联盟之内各用水主体采用公理化协商方式分配水资源的过程,问题(10)的结果就是联盟之内各用水主体通过Nash协商方式分得的水资源量,这一方案满足Nash提出的五个描述分配合理性的公理。 例3说明使用联盟中的参与者之间通过Nash协商方式来分配联盟的均衡水资源分配量的具体过程。 例3:通过Nash协商的方式分配联盟的均衡水资源分配量的计算方法。 一条公共河流流经四个不同的地区,从上游到下游按顺序记为1,2,3,4,所有用水主体组成的集合记为N={1,2,3,4}。假设需要确定联盟结构{[1,2],[3,4]}中联盟[1,2]中参与者1和参与者2的水资源分配方案,且联盟[1,2]得到的均衡水资源分配量为10。 (11) s.t.x1+x2=10,x1,x2≥0 第一个联盟结构{{1,2,3,4}}中,由于所有参与者形成全联盟,他们之间会通过协商的方式分配总的来水量。本文假定的分配联盟水资源的分配方式为Nash协商方法。因此,所有用水主体1,2,3,4通过Nash协商的方式分配100单位的水资源。通过Nash协商方法得到的分配方案为如下优化问题的解 (12) s.t.x1+x2+x3+x4=100, 且∀i∈N,xi≥0 联盟结构{{1,2,3,4}}中,用水主体的总效用为: 并且分配100个单位的水资源。 联盟结构P2={[1,2],[3,4]}中,联盟[1,2]与[3,4]首先通过动态博弈来分配最多100单位的水资源。由于两个相邻联盟之间决策具有先后顺序,因此联盟之间会通过Stackelberg模型的方式在联盟之间总的来水量。确定了各联盟的均衡水资源分配量之后,在每个联盟之内通过Nash协商的方式分配联盟得到的均衡水资源分配量。 (13) (14) 联盟[1,2]内部通过Nash协商的方式分配60的均衡水资源分配量,而联盟[3,4]内部通过Nash协商的方式分配30的均衡水资源分配量。联盟[1,2]中用水主体1,2的Nash协商分配方案为如下优化问题的解 (15) s.t.x1+x2=60,x1,x2≥0 联盟[3,4]中用水主体3,4的Nash协商分配方案为如下优化问题的解 (16) s.t.x3+x4=30,x3,x4≥0 此时联盟结构{[1,2],[3,4]}中,用水主体的总效用为: 两种联盟结构下的水资源分配方案的结果为表1所示: 表1 公共河流的水资源分配方案优劣比较 本文使用具有外部性的合作博弈模型来分析公共河流中的水资源分配问题。此模型把公共河流的水资源分配问题模拟为一个联盟之间竞争、联盟之内合作的博弈问题。得到如下结论:(1)用水主体之间以合作的方式形成联盟,且联盟之间通过竞争的方式分配公共河流的水资源。由于受到河流流向的影响,本文采用动态博弈Stackelberg模型来确定各联盟的均衡水资源分配量,随后在每个联盟之内以Nash协商的方式在联盟中的参与者之间分配联盟的均衡资源分配量,通过最大化Nash协商积来得到每个参与者的资源分配量。比较各种方案下用水主体产生的总效用,可以得到公共河流用水主体之间竞争与合作并存时的最优水资源分配方案。(2)受到外部性环境的影响,部分合作的用水主体产生的总效用可能高于完全合作时用水主体的总效用。此时,公共河流流经的各用水主体在分配水资源时应当综合外部性环境对合作的影响来考虑具体地水资源分配方案,从而提高河流的水资源使用效率。2.2 联盟之间的竞争
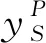
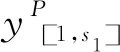
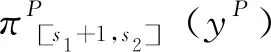
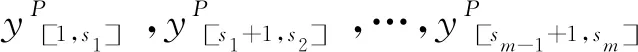
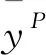
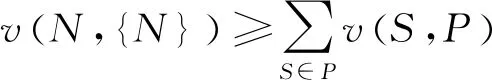
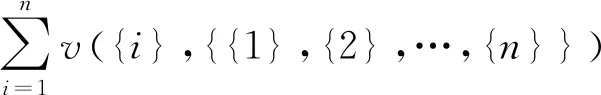
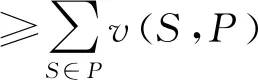
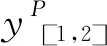
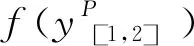
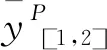
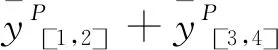
2.3 联盟之内的合作
3 案例分析
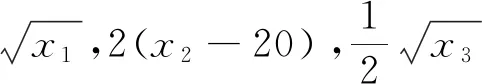
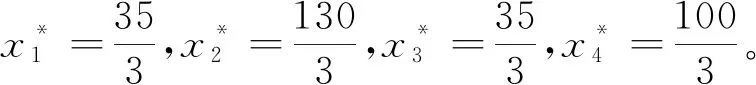

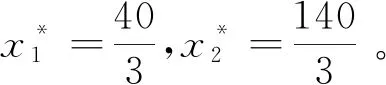
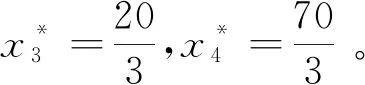

4 结语

