自适应调零天线抗干扰性能影响因素研究∗

侯立志 何 晶 傅玉鑫 周 凯

（1.94498部队 南阳 474370）（2.空军工程大学信息与导航学院 西安 710077）

1 引言

卫星导航系统中，由于导航卫星发射功率较低，信号到达地面时最小信号功率仅为-160dBW，信号完全淹没于噪声之下，信噪比极低；同时，由于卫星导航信号的工作频率是公开的，所以卫星导航接收机极易受到有意或者无意的干扰，抗干扰性能较差。针对卫星导航接收机存在易受干扰的弱点，目前已经研究开发出多种抗干扰技术来提高其抗干扰性能，其中最具代表性的当为自适应调零抗干扰技术［1］。自适应调零天线是一种广义的智能天线，它能够根据实际的信号和干扰环境，灵活地改变各个天线阵元的加权系数，自动地调节天线方向图形状，对干扰信号进行有效的抑制，从而实现对目标信号的最佳接收［2］。在自适应调零天线抗干扰算法中，功率倒置（Power Inversion，PI）算法应用较为广泛［3］。该算法的本质是一种空域滤波抗干扰技术，它不需要预先知道有用信号的特性和干扰入射方向等先验信息，对强干扰环境下微弱目标信号的接收非常有效。以自适应调零天线为主的空域滤波技术成为目前卫星导航接收机广泛采用的抗干扰方法，而合理可信的抗干扰性能测试方法是对终端抗干扰性能进行合理评估的基础。本文在Matlab环境下以PI算法为基础设置合理仿真参数，通过改变干扰源个数、干扰入射角度以及干扰功率的大小，能够直观观察自适应调零天线阵列方向图的变化，判断干扰个数、干扰角度及干扰功率对自适应调零天线抗干扰性能的影响程度，对其抗干扰性能的测试及其对抗方法提供了理论依据。

2 功率倒置自适应调零算法模型

自适应调零天线抗干扰信号处理模型如图1所示［4］。首先，输入信号经过天线阵列接收，然后通过下变频器和A/D数据转换，最后经调零波束形成网络进行干扰抑制处理，提高输出信号精度，实现抗干扰效果。

图1 自适应调零天线模型

天线每个阵元接收的信号用向量x(n)表示，w为每个阵元通道信号的加权矢量，经过自适应处理器加权处理后，天线阵列的输出为

自适应调零技术的核心是求出最优加权矢量，通过这个加权矢量对各个通道进行加权，从而实现干扰抑制。目前，求解最优权值的算法主要有SMI（直接矩阵求逆）、RLS（迭代最小二乘）、LMS（最小均方误差）、PI（功率倒置）等。其中，LMS在卫星导航自适应调零天线阵列处理中是最常用的、鲁棒性最强的自适应处理算法。功率倒置（PI）算法是最小均方（LMS）算法的变形，所采用的最优化准则是最小均方误差准则。信号功率越强，PI算法形成的零陷深度越大，因此，会在强干扰方向上形成较深的零陷，而在弱信号方向上无法形成有效零陷，从而达到抑制干扰，提高输出SINR的目的。

PI算法是将天线阵元分为两部分，第一个阵元作为主阵元，该阵元接收到的信号作为自适应算法的参考信号d(n)，其它M-1个阵元作为辅助阵元。将参考信号d(n)与阵列输出信号做差，得到误差信号e(n)：

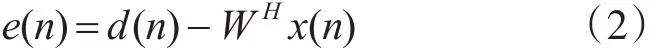
根据最小均方误差准则，使性能函数ξ=E[e2(n)]取最小的点即为最佳权值点。再根据最陡下降法，梯度方向是ξ值增加最快的方向，所以梯度的负方向就是ξ值减少最快的方向［5～6］。因此，我们采用递推公式（3）调整w以寻求wopt：

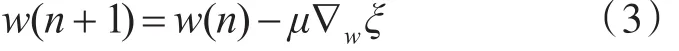
PI处理算法采用如下的梯度估计值：

即它用瞬时输出功率误差的梯度来代替均方误差梯度的估计值。经过多次迭代达到权值最优。

权矢量向最优权矢量逐渐逼近的过程中，新的权矢量等于前一权矢量加上输入信号矢量与误差值的乘积［7～8］。参数 μ 为决定自适应步长、控制收敛速率和稳定性的常数因子。得到最优权值后，再经过式（1）对各个阵元通道进行加权处理，即可在强干扰方向上形成较深的零陷，而在弱信号方向上不会形成零陷，从而达到抑制干扰，提高输出信干噪比的目的。

3 影响因素分析

对于空域滤波而言，若阵元数为N，则理论上最多能产生的零陷数为 N-1［9～10］，但在实际应用环境中，综合考虑到尺寸、费用以及功耗等因素的影响，阵元数量也会受到限制［11～12］。在以下仿真分析中，以7阵元均匀圆阵作为卫星导航接收机自适应调零天线的布阵形式，阵元间距取半个波长，对不同干扰条件下的PI算法抗干扰性能进行仿真分析，从而得出干扰数量、干扰仰角、干扰功率对自适应调零天线的抗干扰性能的影响。

3.1 干扰数量

设干扰源数量为5，干扰来向的仰角向量为[30°,30°,30°,30°,30°]，方位角向量为 [0°,60°,120°,180°,240°]，干扰功率均取为30dB，导航信号已完全被接收机内部噪声淹没，数据采样点数量取为4000，干噪比取为40dB，权值初始化向量设置为[1,0,0,0,0,0,0]，步长因子取为0.02，PI算法下7阵元均匀圆阵输出俯视方向图如图2所示。

图2 干扰数量为5时PI算法下7阵元均匀圆阵输出俯视方向图（俯仰角=30°）

在图2的仿真参数下，在方向角为300°方向加入1个干扰源，俯仰角也保持30°，功率也为30dB，此时干扰源数量增至6，PI算法下7阵元均匀圆阵阵列输出方向图如图3所示。

图3 干扰数量为6时PI算法下7阵元均匀圆阵输出俯视方向图（俯仰角=30°）

由图2、图3可以看出，在干扰仰角为30°情况下，当有来自5个不同方位相同功率的干扰时，7阵元均匀圆阵自适应调零天线基本上能获得正确的阵列输出方向图，而当继续增加干扰至6个时，调零天线已经完全失效，零陷点位置几乎全部错误。

由以上仿真结果可以得出，在一定干扰数量范围内，自适应调零天线能产生正确的零陷点，输出正确的天线方向图，但随着干扰源数量的增加，零陷点位置出现偏移，直至完全错误，抗干扰作用失效。

3.2 干扰仰角

在图2的仿真参数下，将干扰俯仰角分别改为20°和10°，PI算法下7阵元均匀圆阵输出俯视方向图如图4、图5所示。

图4 俯仰角为20°时7阵元圆阵方向图

在图5的仿真参数下，将240°方向干扰源去掉，使干扰源数量减至4个，其他仿真条件不变，PI算法下7阵元均匀圆阵阵列输出方向图如图6所示。再将180°方向干扰源去掉，使干扰源数量减至3个，其它仿真条件不变，PI算法下7阵元均匀圆阵

阵列输出方向图如图7所示。

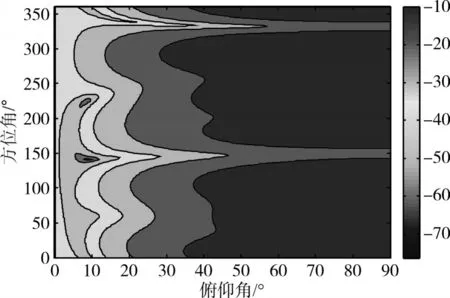
图5 俯仰角为10°时7阵元圆阵方向图

图6 PI算法下4干扰源俯视方向图

图7 PI算法下3干扰源俯视方向图

由图4、图5、图6、图7可以看出，当干扰俯仰角减小时，自适应天线调零能同时抑制的干扰数量会进一步减少。在干扰仰角为20°时，7阵元阵列能抑制4个干扰；在干扰俯仰角为10°的情况下，7阵元均匀圆阵能基本正确的同时抑制的干扰数量减至3。根据图2的仿真条件，干扰仰角的减小实际上表示的是干扰来向更加分散。

由以上仿真结果可以得出，自适应调零天线抗干扰性能与干扰仰角的分散程度有直接关系，干扰仰角越小，自适应抗干扰性能越差。

3.3 干扰功率

在上述仿真参数中，不同来向干扰的功率都为相同值30dB，下面考虑功率大小不同时的情况。设干扰数量为5，干扰来向仰角向量设为[30°,30°,30°,30°,60°]，方位角向量设为 [60°,120°,180°,240°,300°]，其它仿真参数同图2，当只有5个功率相同的不同来向干扰进行干扰时，由图2的仿真结果可知，此时的7阵元均匀圆阵能够在干扰方向上形成准确的零陷，若在此基础上，将来向为[60°,300°]的干扰功率设置为40dB，则PI算法下7阵元均匀圆阵输出俯视方向图如图8所示。

图8 PI算法下7阵元均匀圆阵输出俯视方向图（第5个干扰来向为[60°,300°]，功率为40dB）

若将图8仿真参数中的第5个干扰来向改为[80°,300°]，其余条件不变，则PI算法下7阵元均匀圆阵阵列输出俯视方向图如图9所示。

图9 PI算法下7阵元均匀圆阵输出俯视方向图（第5个干扰来向为[80°,300°]，功率为40dB）

将图8仿真参数中的第5个干扰的功率设置为50dB，其余条件不变，则PI算法下7阵元均匀圆阵阵列输出俯视方向图如图10所示。

图10 PI算法下7阵元均匀圆阵输出俯视方向图（第5个干扰来向为[60°,300°]，功率为50dB）

由图8、图9、图10可以看出，在干扰功率大小不一且有一定夹角的情况下，采用PI算法的7阵元均匀圆阵阵列只能在强干扰方向上形成较深零陷，而对于弱干扰方向造成的衰减明显减小。因为在某方向上出现强干扰时，PI算法会把与强干扰方向有一定夹角的弱干扰视为“有用信号”来处理［13］。强弱信号功率差距越大，自适应调零天线越能在强干扰方向形成较深零陷，而在若干扰信号方向上无法形成零陷，弱干扰是相对于强干扰而言的。

由以上仿真结果可以得出，干扰功率分布大小不同对自适应调零天线抗干扰性能有直接影响。干扰功率大小不一且入射方向有一定夹角时，自适应调零天线阵更容易在功率较大的干扰方向形成零陷，而对功率较小的干扰方向表现不敏感，甚至形成错误的零陷点。

4 结语

笔者建立了基于功率倒置自适应调零算法的模型，通过设置仿真参数，在Matlab环境下的仿真结果直观显示了干扰源个数、干扰仰角的分散程度以及干扰功率大小对自适应调零天线抗干扰性能的影响程度，为建立更加合理完善的暗室测试和外场测试方案提供了理论参考，同时也为如何对抗敌方自适应调零设备提供了一种思路。笔者仅在理论上对影响因素进行了分析，下一步将对实际的测试方案展开进一步研究。