导数在近年高考压轴小题中的应用

赵爱华

(新疆乌鲁木齐市教育研究中心 830002)

导数及其应用是高中数学的重要教学内容，也是高考重点考查内容.近年来，全国卷在选择题的第12题，或填空题第16题陆续出现导数压轴小题，考点设置或明或暗，全面考查高中数学主要内容.我们不妨来分类研究，以提高我们教学的针对性和有效性.

一、导数在三角函数中的应用

例1(2018年高考数学全国Ⅰ卷理科第16题)已知函数f(x)=2sinx+sin2x，则f(x)的最小值是____.

分析此题中函数是将正弦函数两次变换相加而得，第一次纵坐标伸长为原来的两倍，横坐标不变；第二次横坐标缩短为原来的一半，纵坐标不变.题面很熟悉，但是这个加号使得题目变得不同寻常.因此，我们考虑应用导数，找到极值点，求出极值，最后取极小值作为最小值.

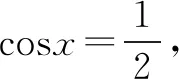
评注本题属于三角函数创新题，依靠常规的三角运算和方法作答有些困难.通过逻辑推理，几何直观可以发现，本函数连续且有界.考查学生应用知识的能力，把极小值转变为最小值.这里有一定的三角运算，这些正是数学的部分核心素养.

二、导数在立体几何中的应用

例2 (2017年高考数学全国Ⅰ卷理科第16题)如图1，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC、CA、AB为底边的等腰三角形，沿虚线剪开后，分别以BC、CA、AB为折痕折起△DBC，△ECA，△FAB使得D、E、F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为____.

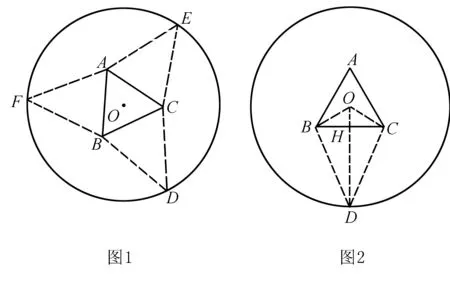
分析连接OD，交BC于H，如图2,设OH=x，根据各边的长度关系确定BC，DH，求解三棱锥的高以及△ABC的面积，进而得到三棱锥体积V的解析式.显然三维空间带来了高次函数，只有借助导数，才能确定最大值.

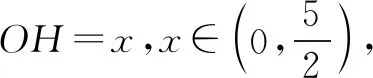
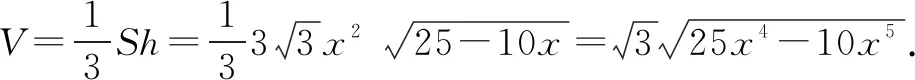
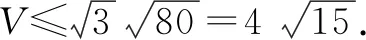
评注本题以立体几何的折叠问题为背景，考查导数的应用.学生首先要能理解题意，合理设置变量，构造函数，然后应用导数的三大功能：求函数的单调区间、极值、闭区间上最值解决实际问题.数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大核心素养都得到了很好地考查.

三、切线在切线问题中的应用

例3 (2016年高考数学全国Ⅱ卷理科第16题) 若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，b=____.

分析切线问题是导数中最常见最简单的问题，但本题中公共切线把导数基础知识和整体代换技巧融为一体，把神秘的超越方程等价转化为可运算的简单方程，方程组思想使待定系数法能顺利实施.

解设直线y=kx+b与曲线y=lnx+2相切于P(x1，y1)，直线y=kx+b与曲线y=ln(x+1)相切于Q(x2，y2).

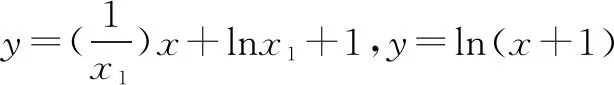
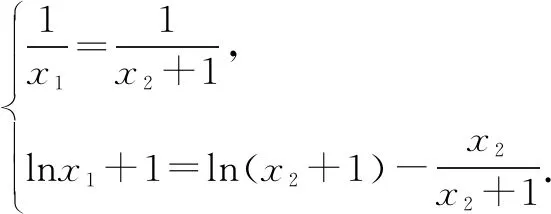
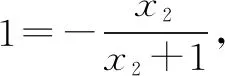
评注本题属于导数问题中最朴素的问题，但是公切线又赋予了问题新的内涵，融合了一些数学运算技巧，将抽象运算变得可操作，使题目档次上升，成为小题把关题.数学抽象、逻辑推理、数学运算、数据分析等核心素养融入其中.

四、导数在抽象函数中的应用

例4 (2015年高考数学全国Ⅱ卷理科第12题)设函数f′(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x>0时，xf′(x)-f(x)<0，则使得f(x)>0成立的x的取值范围是( )

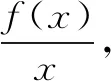
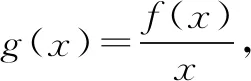
评注本题是抽象函数问题，综合考查函数和导数的性质，要求学生逻辑推理严谨，数据分析到位，数学运算准确，否则极易选成干扰项.本题在导数知识的应用方面是一个很好的范例.对于这种创新试题，试图通过刷题来提升水平的学生，可能感到棘手.

五、导数在极值问题中的应用

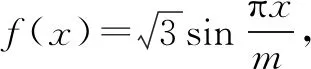
分析从极值点、极值概念入手，从概念中抽象出数据.正确理解存在性，将抽象不等式具体化，合理建模使导数和不等式有效沟通即可求解.

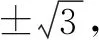
评注本题以三角函数和复合函数为背景，以存在性为依托，考查导数中重要概念极值、极值点.只有概念清晰的学生才能发现[f(x)]2=3，以及解出极值点.导数和不等式的知识巧妙结合，通过正确严谨推理，达到解决问题的目的.本题考查了学生综合运用知识的能力，是以后教学的一个很好的素材.

六、导数在数列中的应用

例6 (2013年高考数学全国Ⅱ卷理科第16题) 等差数列{an}的前n项和为Sn，已知S10=0，S15=25，则nSn的最小值为____.

分析题目表象考查等差数列，但是等差数列的前n项和Sn是关于n的二次函数(公差不为0)，那么nSn就是关于n的三次函数，三次函数的最值需用导数求解.注意到定义域的离散型，该三次函数的极值还未必是最值，因此，还要结合单调性才能作答.

解设数列的首项为a1，公差为d，则

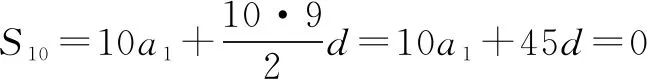
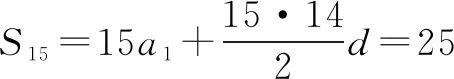
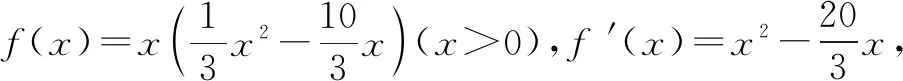
对于nSn而言，n∈N+当n=6时，6S6=-48，当n=7时，7S7=-49，所以nSn的最小值为-49.

评注本题在数列、导数和函数的交汇处命题，导数的应用具有隐蔽性.考查学生是否真正掌握了数列的函数特性，否则无法抽象出这个三次函数.还有三次函数求最值与数列的最值还有区别，也有联系.这在考查数学抽象、数学建模、数学运算、数据分析等核心素养方面，是一道有高度，且高度适中的好题.

高考中导数的试题视角宽广，立意新颖，年年推陈出新.选材紧扣教材，高于教材，与高中数学各分支模块均有联系，背景灵活多变，设问巧妙.导数重点考查通性通法，突出考查单调性、极值、最值的应用.将“考基础、考能力、考素质、考潜能”四合一，充分体现了“培养和提高学生的数学核心素养”课程理念，具有较强的区分度，确保高校准确选拔优秀人才.