基于共形网格技术的ATEM三维数值模拟

嵇艳鞠，任桂莹，关珊珊†，黎东升

（1.吉林大学 地球信息探测仪器教育部重点实验室，吉林长春130026；2.吉林大学 仪器科学与电气工程学院，吉林 长春130026；3.吉林大学国家地球物理探测仪器工程技术研究中心，吉林长春130026）

航空瞬变电磁方法（Airborne Transient Electromagnetic Method，ATEM）采用飞行器搭载电磁系统对大地的二次场进行快速测量，通过分析二次场获得地下电阻率分布，从而了解地质体的构造.相比于地面瞬变电磁法，航空瞬变电磁具有探测速度快，范围广，可在短时间内获得较多信息等特点，更适用于森林、沼泽、割裂地形、山区等地形复杂区域的勘探.航空瞬变电磁法在国内外发展较为迅速，在浅覆盖区寻找金属矿、隐蔽洞体等典型目标体探测方面起到了重要的作用[1-4].常用的瞬变电磁三维正演模拟方法包括有限差分法、积分方程法、有限元方法等，其中有限差分法具有数学表达简单、直观高效等特点，因此发展得较为成熟.Wang等人[5]采用有限差分法进行瞬变电磁三维数值模拟.Commer等[6]2004年利用并行有限差分方法实现了电性源瞬变电磁三维数值模拟，2015年对时间步长进行了改进以减少计算时间[7].Li等人[8]基于有限差分法研究了含水结构的瞬变电磁三维数值模拟.随着瞬变电磁探测技术的发展，地下复杂三维异常体结构的精细化勘探得到关注，采用传统的时域有限差分（Finite Difference Time Domain，FDTD）方法进行地下不规则异常体的数值模拟时，常常会由于边界处网格的阶梯状网格近似导致较大误差，故如何处理复杂异常体的边界问题以及提高三维不规则体的计算精度，成为地球物理勘探中的热点问题.Cao等人[9]提出了自适应有限差分方法，采用局部细化的方式提高了三维不规则异常体的模拟精度，但增加了计算的复杂性.Chang等人[10]采用非均匀网格方式对煤矿充水区域的全波形瞬变电磁响应进行了数值模拟，但网格剖分较难.徐岩等人[11]在瞬变电磁三维正演模拟时，将起伏地形或不规则体表面网格进行了精细剖分，虽然提高了计算精度，但会增加计算量.

共形网格技术是近年来新兴的一种数值模拟技术，它基于有限差分方法，对目标体边界进行特殊处理，以减小传统FDTD方法所产生的阶梯状网格近似误差，提高了有限差分方法的计算精度，在不增加网格数量的基础上，提高了计算效率.Ilinca等人[12]将共形网格技术应用于材料物理学中，解决了材料复杂界面的热传递问题.Wang等人[13]提出了一种改进的时域有限差分共形方案，可快速预测雷达截面以及复杂三维结构的感应电流分布.Guo等人[14]利用改进的共形FDTD网格划分算法模拟复杂三维模型.武超[15]将共形网格技术应用于无线电物理方面，研究了复杂目标的电磁特性计算.范宜仁等人[16]将共形网格技术应用于随钻电磁波测井响应数值模拟中，为随钻快速反演提供支持.Nicolas等人[17]提出了一种基于六面体网格的共形方案，并在材料边缘处进行特定分裂，实现了细化和共形.Wei等人[18]扩展了共形时域有限差分方法，将该方法应用于地震中的弹性波计算，并取得了很好的结果.Cabello等人[19]将共形网格技术应用于雷达散射截面的计算中，取得了较好的效果.但在三维地质体探测中，如何采用共形网格技术更好地拟合曲面异常体的边界问题还有待研究.

本文在传统FDTD方法的基础上，结合共形网格技术开展了航空瞬变电磁的数值模拟研究.基于介质参数等效的思想，更新了传统FDTD方法的电场表达式；对于具有解析式的典型目标体，讨论了基于解析式建模的FDTD共形网格生成过程，采用共形网格技术实现了地下曲面异常体的三维数值模拟，提高了传统FDTD方法对曲面异常体进行数值模拟时的精度.

1 共形网格技术

利用常规FDTD方法进行数值模拟时，Yee元胞仅可以赋一个电导率值，在模拟曲面异常体边界时势必会带来由于阶梯状网格近似而产生的误差.图1为球形异常体二维截面阶梯状网格近似图，介质1表示目标体内部，介质2表示目标体外部，其中阴影区域表示位于目标体表面附近的网格，为了减小误差，在附近网格处，采用介质参数等效技术，更新传统FDTD迭代方程，这种技术叫做共形网格技术，而目标体附近的网格被称作共形网格.

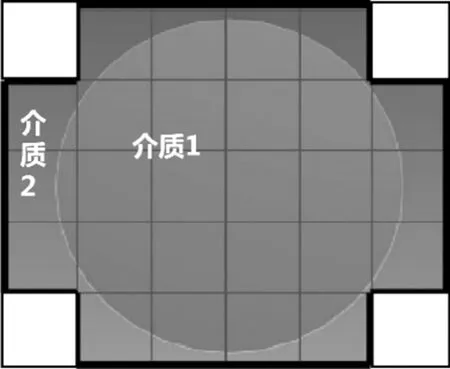
图1 球形异常体二维截面阶梯状网格近似图Fig.1 Spherical two-dimensional section step approximation

在计算时，从曲面异常体的边界出发，确定共形网格，基于线性加权平均思想，重新计算边界共形网格处电场的等效电导率值，将等效电导率代入相应位置的电场表达式，进行更精确的数值模拟[20].其中，对于具有解析式的异常体模型，可直接根据其解析式以及整个计算区域网格的坐标，得到具体共形网格的坐标位置以及需要共形处理的电场所在棱边位置，为异常体表面的共形计算提供参数.

2 基于共形网格技术的电场迭代方程推导

图2为航空瞬变电磁法的工作原理示意图.当发射线圈中通入发射电流时，在整个空间产生一次场，发射电流的瞬间变化在大地中形成涡流并产生二次场，接收线圈接收到二次场后以感应电压的形式记录下来，文中的数值模拟采用发射线圈与接收线圈共中心的方式.

图2 航空瞬变电磁工作原理图Fig.2 Schematic diagram of airborne transient electromagnetic working principle

在用有限差分方法对三维目标体进行数值模拟时，基于Maxwell旋度方程进行差分离散，式（1）和（2）为时域Maxwell旋度方程.常规FDTD方法在数值模拟时，需要将整个计算区域离散成规则的六面体，即近似为图3所示的Yee元胞.电场和磁场在时间上相差半个步长交替取样，Maxwell旋度方程离散后推导得到显式差分方程.拟合复杂模型的曲面边界时，在处理介质共形中，只涉及到电导率的变化，因此只需更新Maxwell方程组的电场迭代方程[21].

式中：e（r，t）为电场强度；b（r，t）为磁感应强度；h（r，t）为磁场强度；j（r，t）为传导电流密度；ε（r）为介电常数.

图3 FDTD中的Yee元胞Fig.3 The Yee cell of FDTD

基于共形网格技术，将传统电场迭代方程中的电导率进行等效替代.图4为共形网格中电导率的等效.图4（a）为三维FDTD共形网格示意图，网格被目标体分为介质1和介质2两部分，由于介质不同，电导率存在差异，因此，需求出共形网格中各电场位置的等效电导率.图4（b）为三维共形网格在xoy面上的投影，介质1的电导率为σ1，介质2的电导率为σ2，介质1与介质2的分界面将一条棱边分为两部分，因电场分布在棱边上，故相应棱边上的等效电导率值由分界面所截长度的线性加权平均得到.式（3）为A边上x方向电场的等效电导率.

以x方向为例，将式（3）代入传统电场迭代方程中，得式（4）所示更新后的电场方程.y、z方向同理可得.

图4 共形网格中电导率的等效Fig.4 Equivalent of conductivity in a conformal grid

3 共形参数确定方法

通过分析三维共形网格可知，在利用共形网格技术进行数值模拟时，其关键是得到需要共形的网格位置以及网格共形参数lz1和lz2.本文以球形异常体表面的共形网格为例，分析说明具有解析式目标体的共形参数确定方法.

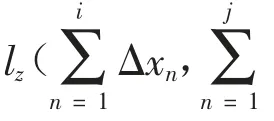
若交点z满足式（5），则可判断z所在的网格编号为k：

设zmin所在的网格编号为kmin，zmax所在的网格编号为kmax，lz1k为z方向编号为k的网格线被目标体所截的内部长度，lz2k为z方向编号为k的网格线被目标体所截的外部长度，由此可得z方向的共形网格坐标及共形参数，如式（6）和式（7）所示.

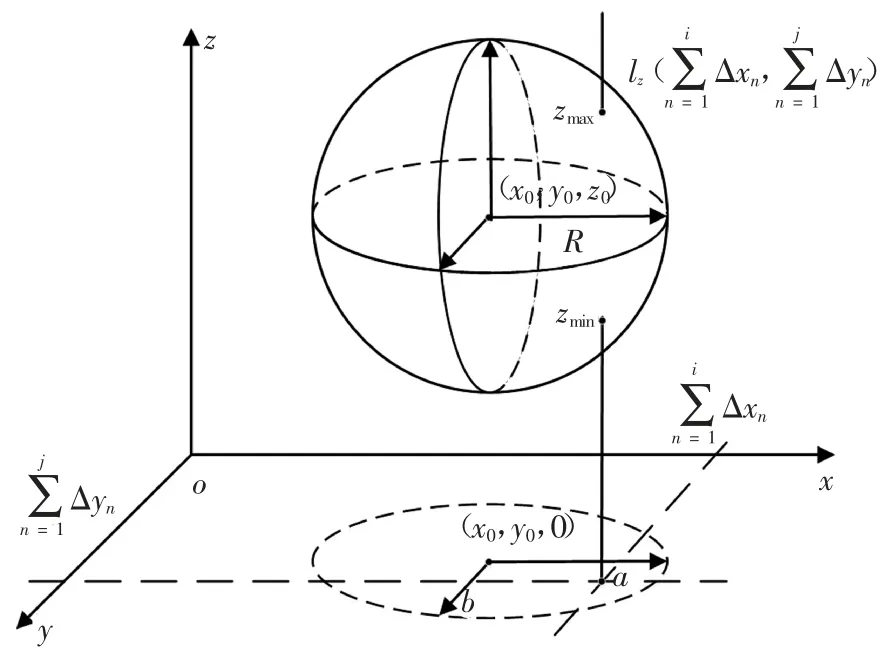
图5 球形异常体共形网格参数示意图Fig.5 Schematic diagram of spherical conformal mesh parameters

同理，可分别得到x方向、y方向的共形网格坐标及共形参数.

4 模型计算及分析

4.1 精度验证

为了验证共形网格技术的有效性，建立5 980 m×5 980 m×3 910 m的包含吸收边界条件的计算区域，大地被剖分为127×127×63个非均匀网格.采用发射与接收共中心的测量装置，发射线圈位于整个计算区域的中心，距地面高度为30 m，发射波形为负阶跃波，电流大小为300 A，其中三维异常体为三棱柱模型，位于发射线圈的正下方，截面为等腰三角形，腰长为，底边长为120 m，三棱柱高度为300 m，三维异常体埋深为250 m，异常体电导率为1 S/m，围岩电导率为0.01 S/m.图6为三棱柱模型设置示意图.

图6 三棱柱模型设置示意图Fig.6 Schematic diagram of the setting of the triangular prism model

在数值计算时，采用加载初始场的方式代替实际探测中的发射源，采用数字滤波算法解决计算式中含有的一阶贝塞尔函数积分问题，之后利用线性滤波方法进行频时转换，得到时间域的初始场值[23-24].

为了验证采用共形网格技术进行数值模拟的有效性，将阶梯状网格近似结果及共形网格处理后结果与有限元方法进行了对比.三棱柱模型截面电导率阶梯状网格近似赋值示意图如图7（a）所示，其中虚线内部近似为异常体电导率值.在利用共形网格技术处理时，需要将共形网格内部电场处的电导率作等效，截面上需共形处理的电场位置示意图如图7（b）所示，以三棱柱截面左侧为例，箭头所在位置表示x、y方向需共形的电场位置坐标.

图7 三棱柱模型截面共形处理示意图Fig.7 Schematic diagram of a conformal mesh of a triangular prism model cross section

图8（a）为阶梯状网格近似和共形网格技术处理后的电磁响应与有限元方法的电磁响应对比图.由于有限元方法采用四面体模拟地下异常体，故该方法可精确剖分三棱柱模型，因此将有限元方法对三棱柱模型的数值模拟作为基准解.由图8（a）可知，3种方法得出的曲线一致性较好.从图8（b）中可以看出，在1 ms之前，两种处理方法的相对误差相差不大，而在1 ms后，可看出利用共形网格技术处理后的相对误差小于阶梯状网格近似方法处理的相对误差，减小了传统FDTD方法在目标剖分过程中引入的阶梯状网格近似误差，验证了共形网格技术的有效性.由于在对三棱柱模型进行阶梯状网格近似时，采用的最小网格为10 m，因此两者之间的误差相差不大，当增大最小剖分网格尺寸后，经共形网格技术处理后的数值模拟优势会更加明显.图8（c）为空中垂直磁场的等值线分布.

图8 三棱柱模型计算结果图Fig.8 Calculation results of the triangular prism model

4.2 球形异常体模型的数值模拟

采用与4.1节中同样的系统模型参数，建立4 060 m×4 060 m×2 950 m的包含吸收边界层的计算区域，大地被剖分为111×111×77个网格.初始场及时间步长的选取方式与4.1节相同.在发射源的正下方设置球形异常体模型，半径为100 m，埋深为100 m，剖分异常体的网格步长为10 m，计算区域示意图如图9（a）所示.以球形异常体的最大横截面为例，作如图9（b）所示的球形异常体截面阶梯状网格近似示意图，并将与球形异常体边界有交点的棱边处的电场进行共形处理.其中，异常体电导率为1 S/m，围岩电导率为0.01 S/m.球形异常体模型基准解采用5 m×5 m×5 m的小网格进行剖分.计算区域不变，将球形异常体附近网格剖分成5 m×5 m×5 m的小网格，此时大地被剖分为163×163×160个网格，将此时的电磁响应作为基准解进行分析.图10（a）为阶梯状网格近似和共形网格技术处理后的电磁响应与基准解的电磁响应对比图.图10（b）为两种处理方法的相对误差曲线，从图中可以看出在0.4 ms之前，两种处理方法的误差相差不大，而在0.4 ms后，共形处理的相对误差明显小于阶梯状网格近似处理的相对误差，共形网格技术在处理复杂异常体边界问题时具有明显优势，相对误差减小了1.65%.图10（c）为空中垂直磁场的等值线分布图.

图9 球形异常体模型设置示意图Fig.9 Schematic diagram of the sphere model setting

图10 球形异常体模型计算结果图Fig.10 Calculation results of sphere model

图11为球形异常体电磁响应切片图，异常体由于埋深较浅，对源的影响在早期较为明显，随着时间的推移，电磁响应逐渐向下、向外扩散，且响应逐渐减小.

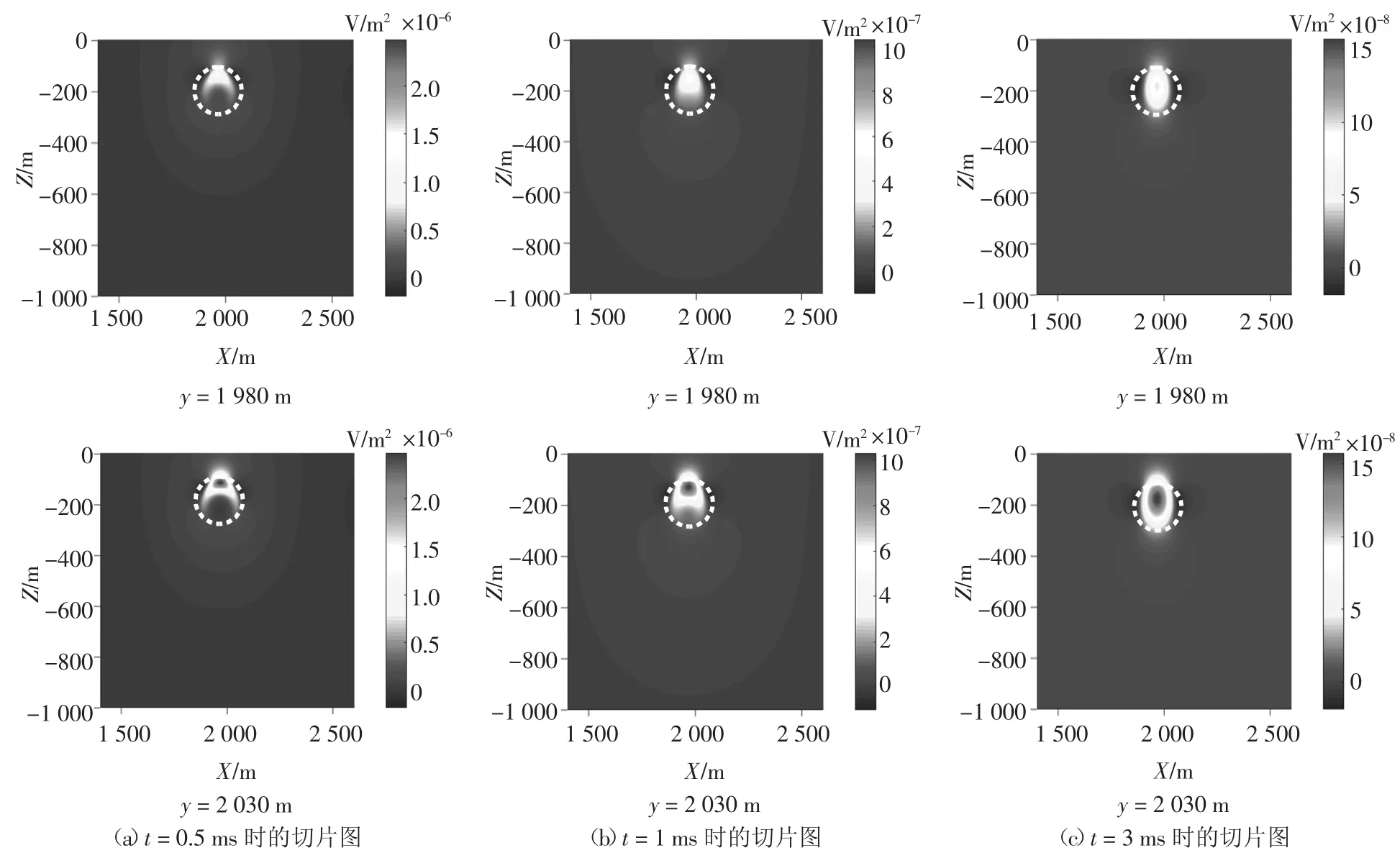
图11 球形异常体电磁响应切片图Fig.11 Electromagnetic response slice diagram of spherical anomalous body

4.3 椭球形异常体模型的数值模拟

系统模型参数的选取方式均与4.1节相同.计算区域及网格剖分数与4.2节相同.在发射源的正下方放置一个半长轴a=150 m，半短轴，埋深为100 m的椭球形异常体，采用基于解析式建模的共形网格技术求解椭球形异常体的时间域电磁响应.图12（a）为计算区域示意图，图12（b）为椭球截面阶梯状网格近似示意图.其中，异常体电导率为1 S/m，围岩电导率为0.01 S/m.将椭球形异常体附近网格剖分成5 m×5 m×5 m的小网格，网格剖分数同4.2节中的描述，以此时的电磁响应作为基准解进行分析.图13（a）为阶梯状网格近似和共形网格技术处理后的电磁响应与基准解的电磁响应对比图.图13（b）为两种处理方法的相对误差曲线图，从图中可以看出在0.5 ms之前，两种处理方法的误差相差不大，而在0.5 ms后共形处理的相对误差明显小于阶梯状网格近似处理的相对误差，其中相对误差减小了4.64%.与图10（b）中曲线进行比较，在处理椭球形异常体时，共形网格处理的相对误差相对于阶梯状网格近似处理的相对误差减小较为明显.通过分析图9（b）、图12（b）可知，需要共形处理的棱边电场越多，共形处理的效果越明显，精度就越高.

图12 椭球形异常体模型设置示意图Fig.12 Schematic diagram of the ellipsoid model setting

图13 椭球形异常体模型计算结果图Fig.13 Calculation results of ellipsoid model

图14为椭球形异常体电磁响应切片图.通过比较球形与椭球形异常体在t=0.5 ms，y=1 980 m的电磁响应切片图，在电磁场扩散的过程中，能够反映出三维异常体的近似形状，并且椭球形异常体的扩散速度要高于球形异常体的电磁场扩散速度.图15为t=7 ms时，z分别为150、200、250 m时的椭球形异常体感应电动势等值线分布图.

本文分别计算了三棱柱、球形异常体、椭球形异常体作为三维异常体时的时间域电磁响应，在相同运行环境下，计算效率如表1所示.其中三棱柱模型利用共形网格技术以及阶梯状网格近似方法的运行时间分别为2 460 s和2 214 s；球形异常体模型利用共形网格技术以及阶梯状近似方法的运行时间分别为2 743 s和1 447 s；椭球形异常体模型利用共形网格技术以及阶梯状网格近似方法的运行时间分别为2 909 s和1 564 s.由于三棱柱模型的共形参数确定只涉及到二维平面，故相对容易获得，因此与阶梯状网格近似方法的运行时间相比较相差不多，耗时为阶梯状网格近似处理的1.11倍.球形异常体模型和椭球形异常体模型为具有解析式的目标体，需根据解析式确定共形参数，因此在电场和磁场的每一次迭代计算中都需要判断x、y、z三个方向共形网格的位置，即异常体表面与网格相交位置，以及交点所分相应棱边的内外边长.并将共形参数代入迭代式中进行计算，因此与三棱柱模型相比要更耗时，与阶梯状网格近似相比，其时间比值分别为1.90倍和1.86倍.由此可知，共形网格技术可在保证计算效率的同时提高计算精度.

图14 椭球形异常体电磁响应切片图Fig.14 Electromagnetic response slice diagram of ellipsoidal anomalous body

图15 t=7 ms时椭球形异常体感应电动势等值线分布图Fig.15 Contour distribution of ellipsoidal anomalous electromagnetic response at t=7 ms

表1 共形网格技术及阶梯状网格近似计算效率对比表Tab.1 The calculation efficiency comparison of conformal technology and stepped grid approximation

5 结论

本文基于传统FDTD方法，结合了共形网格技术，采用介质参数等效思想，求得了线性加权平均电导率，更新了电场迭代方程；研究了有解析式的三维目标体共形网格技术；采用三棱柱模型验证了共形网格技术的有效性，提高了地下曲面三维异常体的数值模拟精度.主要结论如下：

1）在不改变网格大小及数量的基础上，共形网格技术仅对电导率进行线性加权平均处理，并将计算求得的等效电导率代入传统FDTD电场表达式，更新了电场迭代方程.共形网格技术在保证计算效率的条件下，与阶梯状网格近似方法相比提高了曲面三维异常体的计算精度.

2）可通过三维坐标投影法确定出共形网格位置，进而判断出所截网格棱边位置，以确定出曲面共形参数.

3）在共形网格处理中，网格棱边与异常体边界的交点越多，即需要共形处理的电场越多，共形网格技术的效果越明显，精度提高越多.

本文目前开展的工作主要是针对有解析式的三维目标模型进行共形网格技术的研究，而对于无法写出解析式的任意复杂模型，则应分以下几点进行共形网格技术处理：1）通过3ds Max等建模软件建立三维目标模型.2）根据目标模型，生成.stl文件，导出三角面元数据.3）由三角面元数据，通过编程生成Yee网格坐标以及共形参数，并导入3ds Max中进行可视化.4）结合有限差分方法与共形网格技术进行计算，最终实现任意三维复杂模型的高精度数值模拟.