拉曼谱带多峰拟合的可重复性和函数适合度研究

勾艳蓉，李 秋，薛 凯，王丽捷

（天津职业技术师范大学机械工程学院，天津 300222）

微拉曼光谱技术是近些年发展起来的一种具有无损、非接触、空间分辨率高等优势的微尺度实验力学测试新技术，被广泛用于研究层状材料的晶格结构及力学行为[1-3]、纳米复合材料的力学性能[4-5]、涂层系统的残余应力测量[6-7]等力学问题。拉曼光谱技术进行力学测量的原理是拉曼特征峰的位置移动反映了晶格间距的变化，也就是反映了应变的信息[8]。因此，准确获得拉曼特征峰的峰位移动量是应用拉曼光谱技术进行力学分析的关键。常用来拟合拉曼特征峰的函数有高斯（Gauss）函数、洛伦兹（Lorentz）函数、福格特（Voigtian）函数等。目前已有一些关于拟合函数对于拉曼光谱拟合结果影响的研究，如Yuan 等[9]使用高斯函数、洛伦兹函数、高斯-洛伦兹函数、Voigtian 函数、Pearson 函数拟合矿物晶体、玻璃、液体以及荧光灯发射线的拉曼谱带，发现拉曼谱带的拟合峰位置、强度、面积和半高宽值随拟合中使用的峰轮廓函数的不同显著变化。因此，用哪种函数拟合最适合原曲线轮廓是拉曼光谱数据拟合处理中一个必须要解决的问题。另外，在进行拉曼光谱测量时，常常由于拉曼特征峰位置与拉曼光谱仪采集波数范围不匹配等原因，出现采集到的拉曼谱带不完整（外形有缺口）的情况。不完整谱带和完整谱带的拟合函数选择是否需要区别，则是拉曼光谱数据拟合处理中又一个必须要解决的问题。本文以氮铝钛（TiAlN）涂层的拉曼光谱数据的拟合为例，研究完整和不完整2 种拉曼谱带的多峰拟合问题，比较分别使用洛伦兹和高斯2 种峰轮廓函数拟合的可重复性和适合度。

1 材料和方法

1.1 TiAlN涂层材料

使用阴极电弧/不平衡磁控技术，将TiAlN 涂层沉积在高速钢基底上。沉积温度450 ℃，氮气分压为5.0×10-1～8.0×10-1Pa，沉积偏压为-300～400 V，占空比为50%～70%，Ti、Al 靶电流为60～80 A，沉积时间为120 min。获得的TiAlN 涂层厚度为3 μm，TiAlN 涂层和基底之间有1 μm 厚的过渡涂层氮化钛（TiN）。

1.2 拉曼光谱数据采集及拟合

拉曼光谱数据采集使用Renishaw Ivia Reflex 拉曼光谱仪完成。用50 倍物镜、2 400 线/mm 的光栅，样品表面激光斑点直径小于2 μm。采用静态采集方式，采集中心波数设置为700 cm-1，曝光时间5 s，累积6次。使用Origin 数据处理软件进行拉曼光谱数据的拟合。

2 结果与讨论

实验采集得到的TiAlN 涂层的2 种典型的拉曼光谱如图1 所示，分别展示了无缺口见图1（a）和左侧缺口见图1（b）2 种拉曼谱带的外形。从图1 可以看出多个拉曼模叠加形成的拉曼谱带。TiAlN 的可见拉曼模包括：TA 模（165 cm-1）、LA 模（260 cm-1）、2A 模（480 cm-1）、TO 模（686 cm-1）、LO（799 cm-1）等[10-20]，分别使用洛伦兹和高斯函数，用三峰、四峰、五峰、六峰拟合并对比，发现使用五峰拟合得到的拟合曲线最接近TiAlN 涂层的拉曼谱带轮廓，因此以下研究均采用五峰拟合。

2.1 完整拉曼谱带的拟合

分别使用高斯、洛伦兹2 种峰轮廓函数对TiAlN的完整拉曼谱带的五峰拟合结果如图2 所示。从图2可以看出，使用2 种函数的累计拟合曲线均能较好地拟合完整拉曼谱带，并且可以确定本文测量的TiAlN 涂层的TA 模、LA 模、2A 模和TO 模4 个拉曼模的位置分别在165cm-1、268 cm-1、480 cm-1和686 cm-1附近。

为了比较拟合结果的可重复性，分别使用高斯和洛伦兹2 种函数对同一组数据（包含5 个拉曼光谱）拟合2次，同一组完整拉曼谱带分别用高斯和洛伦兹函数拟合2 次的拉曼频移如图3 所示。

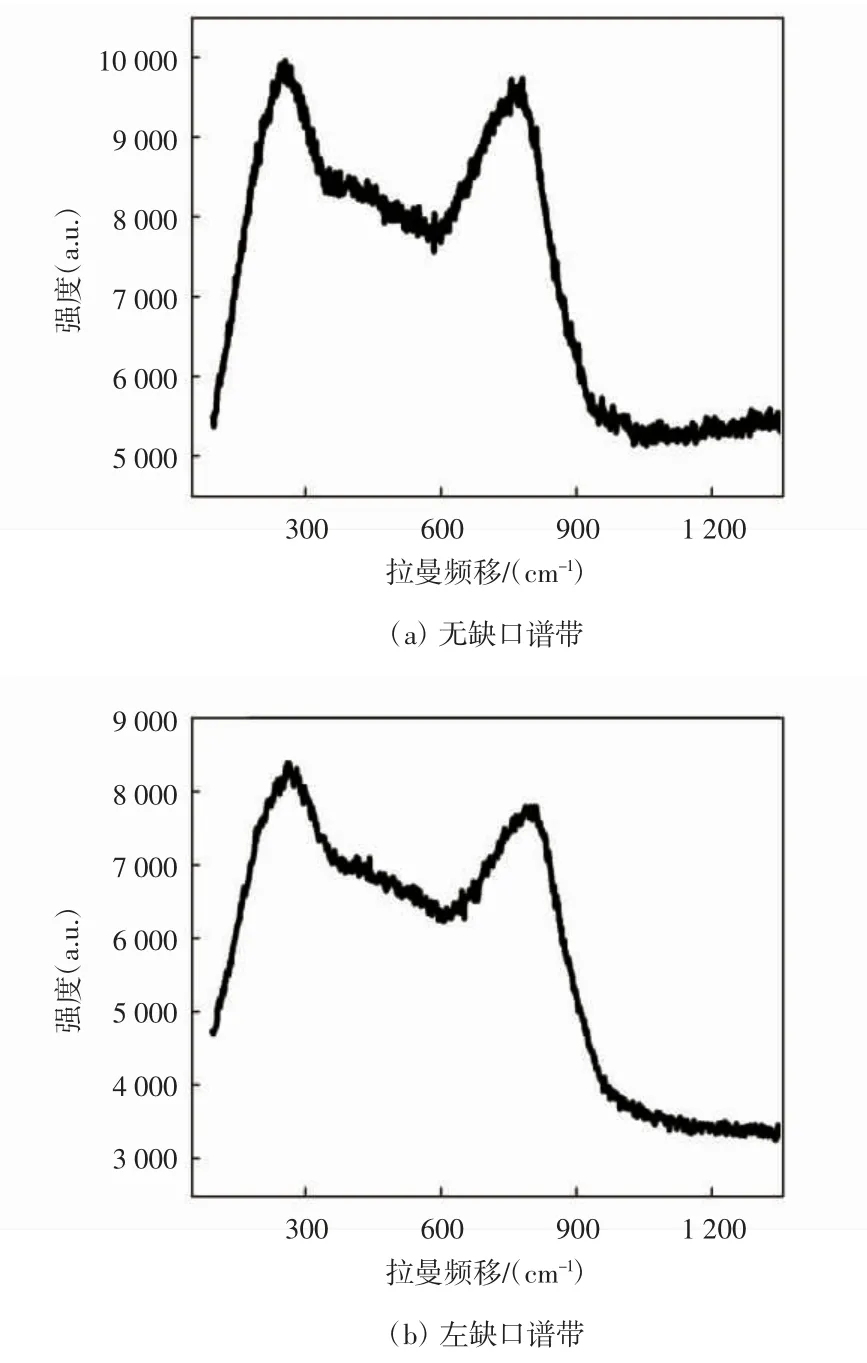
图1 TiAlN 涂层的2 种典型的拉曼光谱

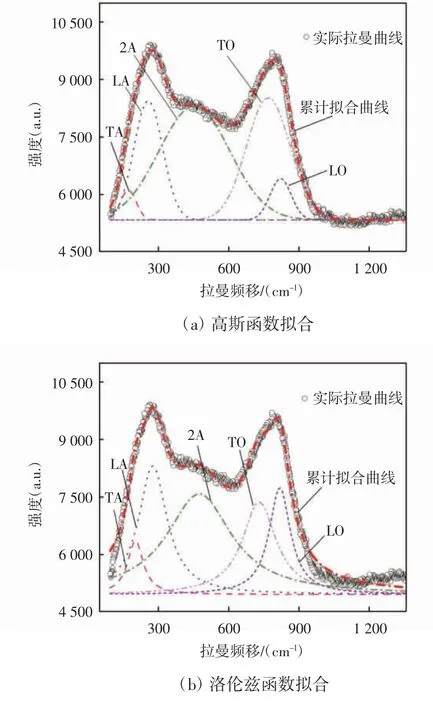
图2 TiAlN 涂层的完整拉曼谱带的五峰拟合结果

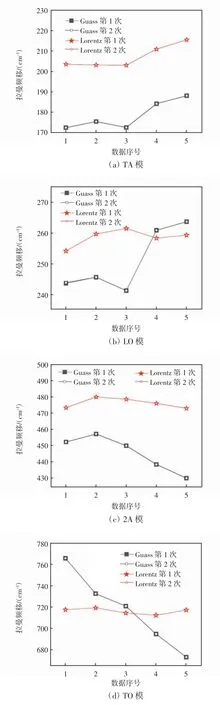
图3 同一组完整拉曼谱带分别用高斯和洛伦兹函数拟合2 次的拉曼频移

由图3 可以看出，用2 种函数拟合2 次的各个峰的峰位均一致，说明对于完整拉曼谱带，用这2 种函数拟合都具有良好的可重复性。

为了比较高斯和洛伦兹2 种峰轮廓函数对于TiAlN 涂层拉曼谱带拟合的适合度，本文提出赤池信息标准测试（akalike information criterion，AIC），即AIC值比较法，该方法是衡量统计模型拟合优良性的一种标准。一般情况下，由AIC=-2log Li+2Vi[21]计算得到（其中Li是模型i 的最大似然，通过Vi自由度参数来确定），为了避免出现过度拟合，所以优先考虑AIC 最小的模型。高斯和洛伦兹函数拟合的AIC 值比对流程如图4 所示。

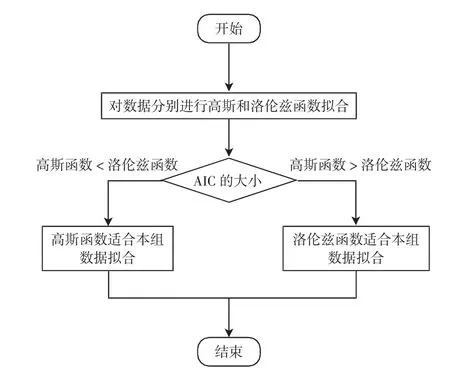
图4 AIC 值比对流程

对于完整拉曼谱带的拟合，使用高斯函数拟合的AIC 值均比洛伦兹函数拟合的小，完整拉曼谱带的高斯和洛伦兹函数拟合的AIC 值对比如图5 所示。图5表明高斯函数比洛伦兹函数更适合完整拉曼谱带的多峰拟合。对于适合程度可以由权重值Δ（AIC）来量化。Δ（AIC）=AIC-minAIC[21]，表征每种模型相对于最佳模型AIC 的差异。分别用高斯和洛伦兹函数拟合完整拉曼谱带的AIC 权重值比对如表1 所示。以1号数据为例，洛伦兹函数适合原始数据的程度是高斯函数的2.78×10-257倍，即高斯函数的适合程度约是洛伦兹函数的3.60×10256倍。因此，对于完整的拉曼谱带，用高斯函数拟合的适合度远高于洛伦兹函数。

2.2 缺口拉曼谱带的拟合

对于左侧有缺口的拉曼谱带，分别使用高斯和洛伦兹函数五峰拟合同一组拉曼数据2 次的结果如图6所示。

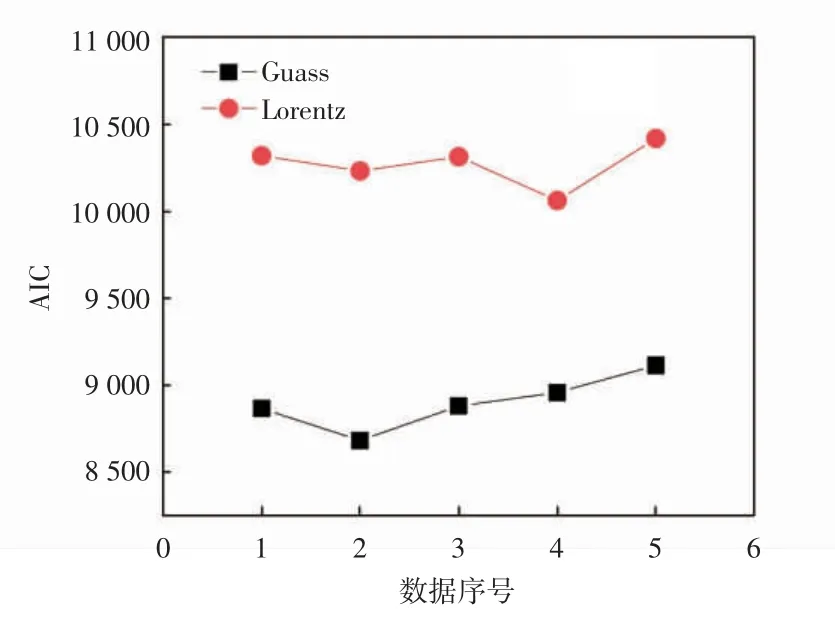
图5 完整拉曼谱带的高斯和洛伦兹函数拟合的AIC 值对比

表1 用高斯和洛伦兹函数拟合完整拉曼谱带的AIC 权重值对比

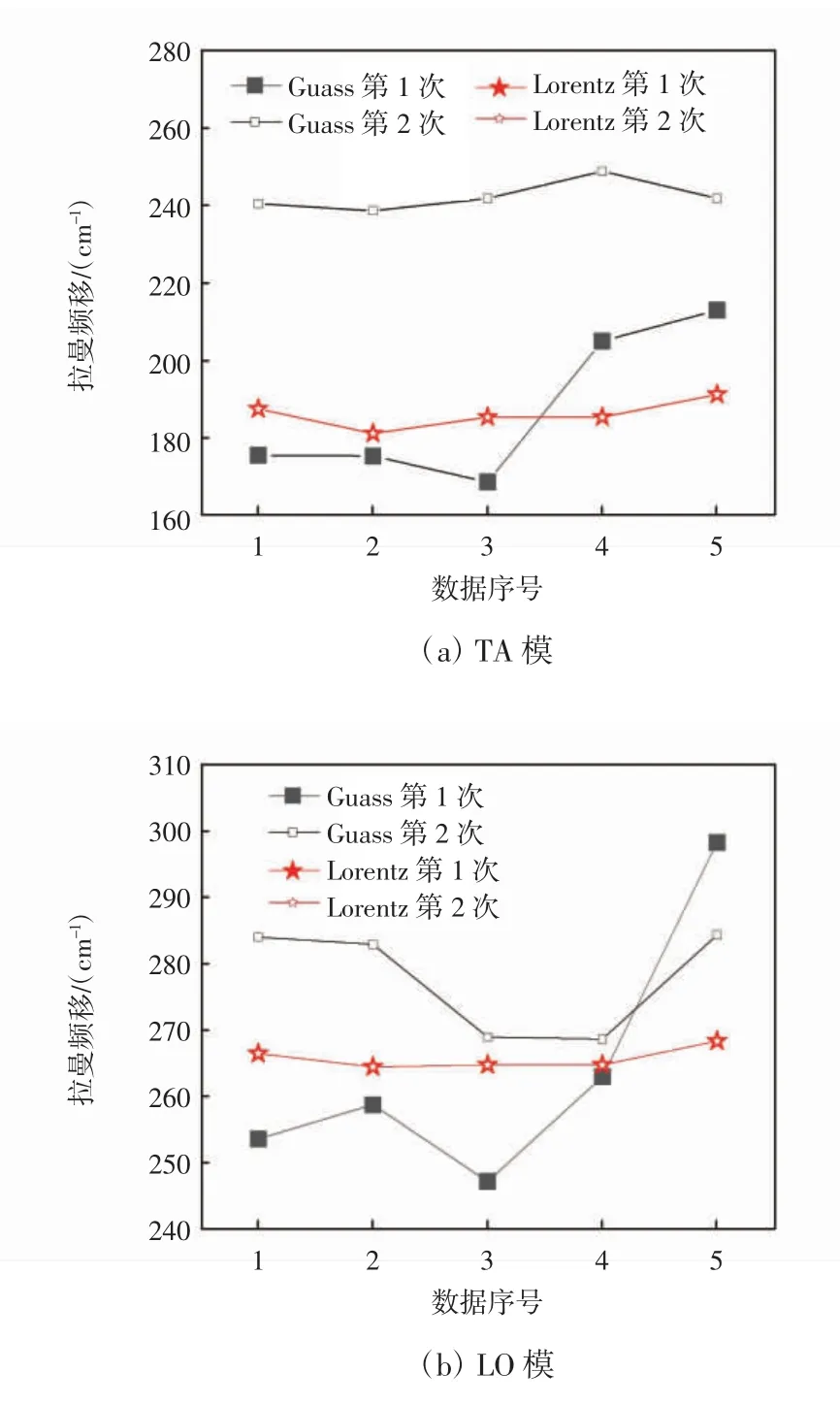
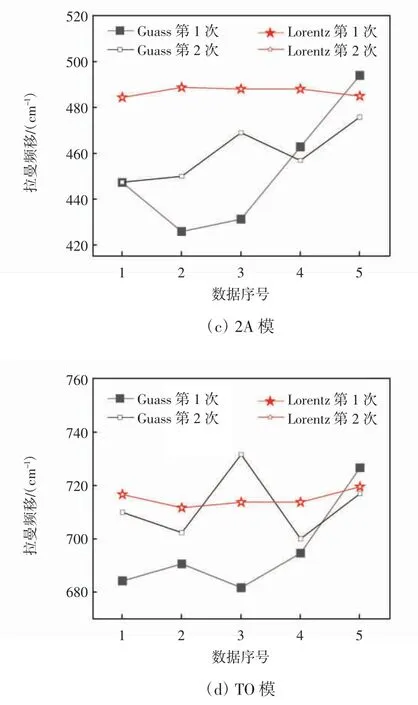
图6 同一组缺口拉曼谱带分别用高斯和洛伦兹函数五峰拟合2 次的拉曼频移

由图6 可以看出，用洛伦兹函数拟合得到的各个峰的峰位一致，而用高斯函数2 次拟合得到的峰位置不同且相差较大，这说明对于缺口拉曼谱带用高斯函数拟合不具有可重复性。

3 结语

本文研究了TiAlN 涂层完整和不完整2 种拉曼谱带的多峰拟合问题，比较了分别用高斯和洛伦兹2 种峰轮廓函数拟合的重复性和适合度。结果表明，对于有缺口的拉曼谱带，使用洛伦兹函数拟合的结果具有良好的重复性，而使用高斯函数拟合的结果不具有可重复性，所以有缺口拉曼谱带的拟合宜采用洛伦兹函数。对于完整拉曼谱带，使用高斯和洛伦兹2 种函数拟合的结果均具有良好的可重复性。本文通过拟合AIC 值的比较，进一步确定了高斯函数比洛伦兹函数更适合拟合完整拉曼谱带。