山岭隧道过破碎岩层开挖面塌方机制与位置预测研究

付廷波

(铁正检测科技有限公司 山东济南 250014)

1 引言

随着交通运输业的大力发展，隧道工程作为道路交通的重要组成部分[1]，正向着长、深、大方向迈进，尤其在地质条件复杂的山区修建过程中，常常面临巨大的挑战。塌方作为隧道修建过程中常见的隧道工程灾害，一经发生，往往造成严重的工程事故[2]，不但会损毁现场施工设备，给企业造成极大损失，还会严重威胁作业人员的生命安全。除此之外，整治塌方严重影响施工进度，二次返修更是难以避免带险作业[3－4]。能否较为准确地预判塌方的几率和塌方的空间位置成为隧道工程界的一大难题。长期以来，专家学者对此做了大量的研究工作，张清[5]采用关键块体理论，确定可能滑动块体在隧道断面上的具体位置；高谦[6]将块体理论的可靠度分析理论和系统突变理论相结合，对围岩的构造控制型失稳形式进行有效预测；刘贵应[7]建立了隧道塌方失稳的尖点突变模型，并给出塌方与否的判据；许建聪[8]采用系统工程科学理论和非线性科学的灰色尖点突变理论，建立围岩－初支系统的灰色尖点突变失稳预测模型，对围岩－初支系统的失稳时间进行预测。

本文依托九绵高速梅家沟隧道，采用FLAC3D数值模拟的方法对隧道台阶法施工进行数值计算，分析了不同开挖进尺下，破碎岩层的塑性区深度和主应力场分布，揭示了开挖面的塌方机制；建立隧道开挖过程中的概化模型，考虑了上覆岩体作用和爆破扰动效应，基于薄层单元体受力理论，采用理论分析方法建立了隧道塌方判别体系，在此基础上对塌方的空间位置进行预测。

2 工程地质概况

梅家沟隧道位于四川省绵阳市平武县境内，隧道区为中山地形。隧道起讫桩号:左线ZK94＋707～ZK98＋680、右线 K94＋650～K98＋703；隧道长度:左线3 973 m、右线4 053 m，设计为分离式特长隧道。隧道设计净空尺寸为10.25×5.00 m，设计时速80 km，隧道进出口设计为端墙式。

隧址区为构造剥蚀高中山地貌，山体浑厚，地形起伏较大，海拔高程1 710～2 288.7 m，相对高差约578.7 m，局部成陡崖状，隧道最大埋深700 m，为穿山隧道。印支期花岗岩:该层分布于整个隧道，由花岗岩组成；花岗岩:灰白色，主要矿物成分为正长石、石英等，粗粒变晶结构，大块状构造，岩质坚硬，裂隙发育，锤击声脆，不易击碎，RQD＝90%，部分陡坡处可见强卸荷带。

隧址区位于北部的文县弧形构造带、西部的岷江－雪山－虎牙关断裂带和东南部的龙门山断裂带所围限的楔形地块上。地块内构造形迹主要受控于上述三大构造带，但后期受文县弧形构造影响均呈现向南突出的弧形弯曲。印支期受SN向构造运动的强烈挤压，形成的一系列近EW向褶皱和断层构成了该区构造的基本格架。

3 塌方机制分析

3.1 模拟方案

本文模拟建立三维数值模型，模型尺寸为(100×80×30)m，如图1所示。边界条件为固定前后左右和下部界面，上部边界为自由面，采用Mohr-Coulomb本构模型，大应变变形模式，先行开挖10 m一般岩性中的隧道，以破碎岩层里程段向前分别模拟不同开挖进尺(0.5 m、1.0 m、1.5 m、2.0 m)下的位移场、应力场和塑性区分布。所选取的围岩力学参数见表1。

图1 数值计算模型及模型边界条件

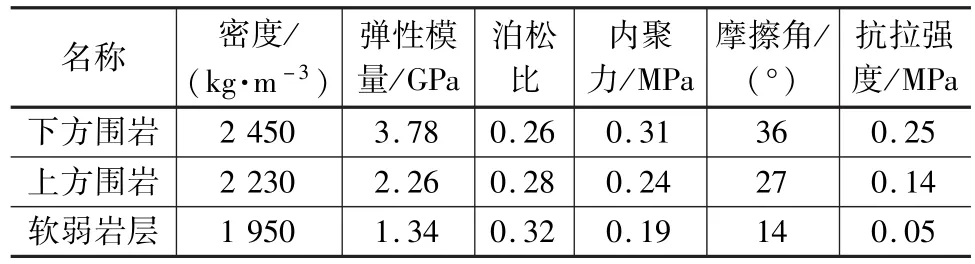
表1 岩体物理力学参数

3.2 数值计算分析

(1)位移场分布

图2～图4为不同开挖进尺下的位移场、主应力场和塑性区分布云图，统计结果见表2。分析可知，当自软弱岩层界面向前方开挖时，随着开挖进尺的增大，围岩拱顶下沉和周边收敛累计值逐渐增大，其中进尺0.5 m时，拱顶下沉和周边收敛分别为241.78 mm和409.24 mm，此时围岩预留量可为300 mm；当进尺为1.5 m时，拱顶下沉和周边收敛分别为309.73 mm，周边收敛为501.38 mm，此时增大围岩预留量会增大岩体滑塌的风险，应提高支护强度，抑制围岩变形继续发展。

图2 位移场分布云图

图3 主应力场分布云图

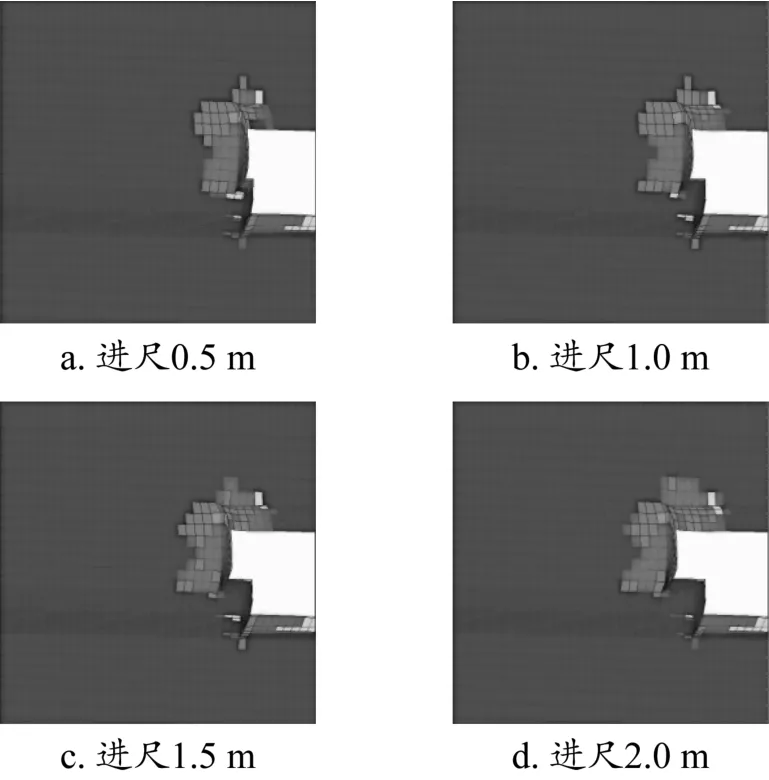
图4 掌子面塑性区分布

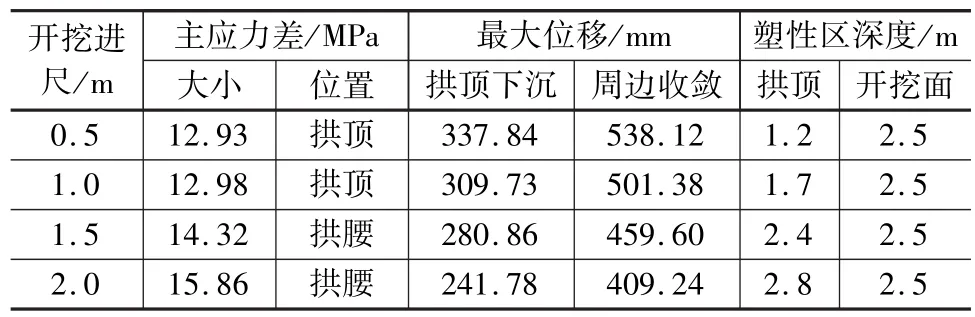
表2 数值计算结果

(2)主应力场分布主应力差决定了岩体是否破坏，主应力差越大，围岩破碎程度越高。当进尺为0.5 m时，主应力差极值为12.93 MPa，出现在拱顶位置；当进尺为2 m时，主应力差极值为15.86 MPa，出现在拱腰位置。表明随着开挖进尺的增大，岩体主应力差极值分布从拱顶向下发展，相应的破碎区范围更大。

(3)塑性区深度分布

掌子面塑性区深度分布与开挖进尺关联性不大，均在2.5 m左右，但塑性破坏模式各异。当开挖进尺比较小时，软弱岩体暴露面积较小，可简化为小跨度简支结构，受后方支护体的承载作用，开挖面主要为受拉破坏，拱顶为剪切破坏。随着开挖进尺的增大，简支跨度随之增大，破坏区范围增大，自承载能力急剧减小，后方支护体对其承载作用增大，开挖面岩体呈现受拉破坏，拱顶由剪切破坏向拉剪破坏转化。对后方岩性较好的岩体塑性区深度影响较大，长度影响较小。

4 开挖面塌方判据及空间位置预测

4.1 力学模型及其假定条件

隧道穿越倾斜岩层时，假定岩层符合下列条件，建立如图5所示的简化力学模型[9－12]。

图5 简化力学模型

(1)软弱岩层为均质岩层，其高度大于隧道净高，上下分界面为平面。

(2)软弱岩层倾向和隧道水平走向夹角为锐角，拱顶位置最先进入软弱岩层。

(3)软弱岩层上覆岩体为均布荷载，等效为竖向重力作用。

(4)掌子面采用爆破开挖，爆破扰动作用力简化为竖向地震力，大小为岩层重力的m倍。

(5)岩层力学本构关系符合摩尔－库伦准则。

(6)假定软弱夹层的竖向滑动面贯穿整个岩层，且不考虑地下水的影响。

4.2 判据推导及建立

隧道在向前开挖时，通过长短距离结合的超前地质预报手段可基本准确掌握前方不良地质体的位置和性状。当开挖面推进至拱顶进入倾斜软弱岩层时，可建立简化力学模型，采用薄层单元受力分析法对该模型进行受力分析，再通过对其分布高度进行积分，基于受力平衡原理，求得塌方的空间位置。

隧道拱顶先后出现两个竖向滑动面AD和BC，在ABCD形成的直角梯形的软弱地质体中，取厚度为dz的薄层单元体，其受力分析见图6。该单元左右两边作用力为水平地应力作用下的竖向摩擦力dF。当隧道开挖面进入软弱岩层的深度不大时，直角梯形体受力保持平衡，随着开挖面的不断推进，受力体系也随之动态调整；当开挖到一定深度时，受力体系达到临界平衡状态，如果软弱岩层厚度足够大，使得达到该临界状态开挖深度时，隧道开挖面尚处于其中，继续开挖则会导致塌方。

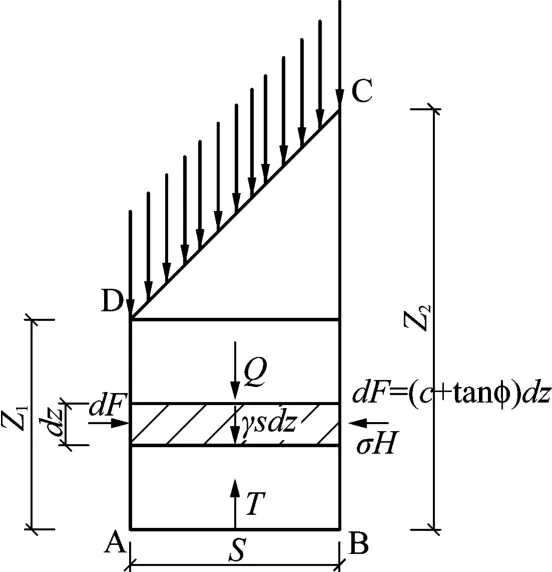
图6 薄层单元体受力分析简图

经上述分析可知，开挖面塌方与软弱岩层的倾角、力学性质、开挖面进入软弱岩层深度、支护作用力、上覆岩层作用、隧道埋深以及爆破扰动作用力有关，据此定义塌方判定抗力函数R:

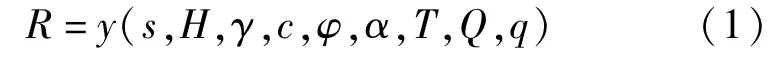
式中，s为隧道进入软弱松散层的深度；H、γ、c、φ分别为软弱岩层的厚度、重度、内聚力和内摩擦角；α为边坡的坡脚；T为初期支护力。

根据摩尔－库伦准则，可求得单元体两侧的摩擦力为:

式中，σH为水平主应力。

假设隧址区侧压力系数为ξ，则可得:

式中，σV为竖向主应力；z为计算点的深度。将式(3)代入式(2)可得到:

根据图5中的几何关系可得:

式中，z1、z2分别为竖向潜在的滑动面BC和AD的长度，与软弱岩层的厚度有关；h为开挖面进入软弱岩层的高度，与软弱岩层的倾角和隧道进入其深度有关。根据图6中单元体的受力条件，可对其两侧面的摩擦力和其重力进行积分，积分后即可得到塌方的判据表达式为:

计算可知，R为s的一元二次函数表达式，化简为:

令R＝0，可化简为一元二次函数等式，得到下列方程:

式中:

由于p＞0，可知一元二次方程(8)的函数图形为开口向上，其根的判别式为:

根据判别式值的正负可对开挖面的塌方与否做出判定，见表3。

表3 塌方判据

当△＞0时，方程的两个不相等的解为:

开挖面发生塌方的条件是R＜0，因此隧道进入软弱岩层的深度s满足:

根据实际情况:

经上述推导，综合考虑软弱岩层的力学性质及埋深、隧道支护作用力、开挖爆破作用力，根据表3可对隧道开挖面洞口塌方与否进行判定，再根据式(13)～式(15)可较为准确地确定塌方发生的空间位置。

5 工程应用

通过上节建立的开挖面塌方判据对梅家沟隧道开挖面塌方的空间位置进行预测分析，根据现场工程地质勘测，得到各项计算参数见表4。其中支护作用力在初期支护施作初期尚未完全发挥其作用，可近似抵消爆破扰动作用力。

表4 现场地层及施工参数

将表4中的参数分别代入式(9)、式(10)、式(11)、式(8)、式(13)，求得一元二次方程的常数项和判别式以及方程解，见表5。

表5 塌方判据应用计算结果

计算可知，当隧道掌子面进入软弱破碎岩层的深度大于1.40 m时可能会发生塌方。根据现场实际情况，对应塌方里程为ZK68＋229.8，而开挖面实际发生塌方的里程为ZK68＋231.4，基本吻合。

6 结束语

(1)隧道开挖遇到围岩岩性突变时，应采用多种预报手段尽可能探明前方地质情况，控制开挖进尺，尽量减小爆破扰动，可有效地降低开挖面塌方几率。

(2)在软弱岩层中开挖隧道，合理的围岩预留变形量可充分让围岩变形，避免支护结构受力过大。过度追求围岩预留变形量则会导致围岩破坏区向深处扩展，对开挖面施工极为不利，建议不超过300 mm。

(3)针对掌子面的松散岩体，应先对其进行加固，改善松散体的物力力学指标，严格控制初支的施工质量，确保初支及时受力。

(4)基于薄层单元体受力平衡建立的开挖面塌方判据，对于无地下水分布的软弱岩层开挖隧道可较为准确地预测塌方的空间位置。