突发公共卫生事件方舱医院建设选址决策研究＊

■ 李刚 林运卫

西安邮电大学经济与管理学院 西安 710121

0 引言

世界各地爆发突发公共卫生事件以来，普遍面临着专科医院不足医治床位紧缺的问题，武汉市此次疫情轻症患者较多，导致医院床位紧缺，于是改建新建方舱医院20 余家，来增加收治能力，结果证明了方舱医院在隔离收容和检验医治方面十分有效。武汉市改建新建方舱医院的成功实践，证明了方舱医院应对高传染性疫情的独特作用，尤其是在疫情大面积传播而轻症患者较多情况下，能有效应对隔离收容和检验医治床位紧张问题，给未来和其他区域应对突发公共卫生事件提供良好借鉴。那么，方舱医院是改建好还是新建好，在哪里选址更科学的问题，引起了广泛的争论，是学界、政府和社会亟需要深入研究的问题。

选址决策问题是国家或地区、工业企业、甚至是家庭，经常需要选择设施设备建设具体地点的难题[1]。学界多研究不同功能场地的选址问题，如国家行政中心、区域物流中心、交通场站、企业配送中心、企业厂房库房等选址问题[2]，但对于应急设施选址问题早期都是凭经验决策，缺乏科学性。1909年，Weber研究了在平面上确定一个仓库的位置使得仓库与多个顾客之间的总距离最小问题(称为Weber问题)[3]，激发了应急设施选址问题的科学理论研究。在此基础上，1964年Hakimi提出了中值问题，中值问题的目标是使所有需求点到设施的平均距离（时间）最短或总运输费用最小[4]，1965年该学者在中值问题的基础上，进一步提出了p-中心问题，目标是在p 个设施中使需求点到最近的设施点最大距离最小化[5]。但因应急设施必须建设在与需求点特定距离之内才能满足特别的需要，如城市消防站，应急避难场所等，以降低总时间或总成本为目标的中值问题对这些应急设施选址并不适用[6]。1971年Toregas 等基于中值问题的不足，提出了集合覆盖模型，即在给定的距离（时间）内，用最少的设施成本去覆盖所有需求点，而当每个设施的成本相同时，问题简化为用最少应急设施数去覆盖所有需求点[7]。由于集合覆盖模型需要覆盖所有需求区域，且模型没有资源约束，该方法得出的应急设施数目往往超过决策者的承受能力，为了改进该缺陷，Richard和Churh 在1974年提出了先固定应急设施数目再确定它们的位置来覆盖所有需求点的最大覆盖模型，有效解决了资源约束的问题[8]。

以上对应急系统的研究只考虑了时间或距离两种因素，但在现实中应急系统通常设置多个目标[9]，方磊2003年研究应急系统选址决策时，兼顾了应急系统时间紧迫性和系统费用最小两个目标[10]，并进一步基于目标规划考虑了权重约束、距离约束、设施数目约束和不同区域发生事故数目等多个选址目标约束因素[11]。陶泽琼2012年基于前者的研究，利用目标规划增加了安全防护能力的目标约束、交通容载能力目标约束、地域繁荣程度目标约束、与周围环境协调性目标约束、文化水平目标约束和生活水平目标约束等语言变量约束，并且运用模糊数处理语言变量，提高了该模型的适用性[12]。这些多目标约束对应急设施科学选址提供了重要依据，但这些约束没有考虑突发公共卫生事件方舱医院的防疫需求，且并没有考虑建设模式决策问题。

方舱医院作为应急设施的一种，考虑到突发公共卫生事件方舱医院的防疫需求和建设模式的选择，本文在以往应急系统选址决策研究的基础上，增加建设工期和疫情防控因素，并结合AHP 和目标规划模型[13-16]，对突发公共卫生事件方舱医院的建设模式和选址决策进行研究。

在供需不匹配导致制造业产能过剩的背景下，从供给侧入手进行结构性改革有利于缓解供需不匹配的现状，但要达到供需匹配良性发展，还需要需求侧的配合，应急设施作为需求侧其选址影响着供给侧物资的及时供应，因此作为特殊应急设施方舱医院的选址更加需要深入研究，本文是2016年国家社会科学基金一般项目（16BGL015）；“互联网+”背景下制造企业供给侧结构性改革路径研究的阶段性成果，本文为该课题的供给侧结构性改革路径研究提供了微观实证。

1 新建改建决策

2020年2月初期，武汉市医院床位严重紧缺，为了解决这一突出问题，武汉市除了参考北京小汤山模式，陆续新建了雷神山和火神山医院用于救治重症患者，又于2020年2月4日，开始改建方舱医院用来收治轻症患者。方舱医院陆续开放了1.3 万张床位，收治了1.2 余万名患者。武汉市所有方舱医院既解决了床位紧缺的问题，也起到了抑制传染扩散和稳住民心的巨大作用。方舱医院有新建和改建两种建设模式，两种模式都可达到隔离、治疗、防疫的作用，但因二者在时间、成本和效果上各有优缺点，有着各自的适用性。因此，疫情爆发后，为了达到能快速收治的目的，也为了防止疫情进一步扩散，首先在预测方舱医院需求的基础上，在平衡建设时间、成本和效果的基础上，需要对新建和改建方舱医院进行决策。本文用AHP 方法依据时间、成本、风险和建筑的可持续性四个准则进行决策，解决方舱医院新建改建的决策问题。

1.1 决策方法

1.1.1 AHP方法

本文采用层次分析法（Analytic Hierarchy Process,AHP）确定新建还是改建方舱医院。

1.1.2 决策准则确定

本文目标层为确定方舱医院建设模式。

准则层有以下4个准则：

（1）成本：成本包括土地购置费或征用费，建设施工费，建筑安装费和各类医疗设施设备购置费等。在原有建筑上改建方舱医院就不需要土地购置费和建筑建设费，只需要室内改造费和医疗设施设备购置费；新建方舱医院则需要从可行性论证到竣工这个过程的全部费用，很明显在成本上，改建比新建更有优势。

（2）时间：在疫情期间，方舱医院的建设工期无疑是一个很重要的因素。宁愿床等人也不要人等床，确诊患者要及时地转到方舱医院进行隔离，防止二次传染和耽误治疗的最佳时机，所以方舱医院建设工期越短越好。改建因为有原有建筑能为方舱医院提供外围结构，只需部分改造工作和医疗设施设备配置时间，而新建方舱医院从动工开始到最后竣工，建设工期明显比改建更长，所以在时间上改建比新建更有优势。

（3）疫情防控风险：突发公共卫生事件方舱医院收治的都是高传染风险患者，该类方舱医院应建在人群不密集的地方，并且最好建在城市的下风向处。虽然随着医疗技术改善，消毒和隔离效果都有大幅提升，但是每次疫情初期，对新型病毒的认识还不全面，方舱医院应尽量选择人群密度较低的地方。改建方舱医院多由体育馆和会展中心这类容积大的建筑改建而成，但这类公共建筑都是城市的商业中心或生活小区集中区域，其人群密度比较大，且建筑不能满足医院设计的核心内涵，不能兼顾医院管理、公共卫生、隔离防传染、防止污染环境等全面要求，因此，具有较高风险。新建方舱医院，则需要按照标准，如《新型冠状病毒感染的肺炎传染病应急医疗设施设计标准》建设，建筑和所有系统及设备具有严苛标准，新建恰好在选址和建设时就可以避免这些风险。所以在疫情防控风险这个这准则下，新建比改建更有优势。

（4）建筑的可持续性：随着节约型社会的推进和响应绿色建筑的倡议，不管是改建还是新建，都需要考虑抗疫之后，该建筑该如何可持续使用。改建的方舱医院在抗疫后可迅速恢复原来结构和功能，很短时间内能继续承担其使命。而新建方舱医院，对传染病收治具有专业性针对性，疫情结束后，如果继续以方舱医院的功能运营，就会产生更高的运营费用而浪费资源，若改做他用或拆除则会浪费更大。因此从建筑的可持续性发展来看，改建比新建更有优势。

方案层为新建方舱医院和改建方舱医院。

（1）建立评价对象的层次分析结构，如图1所示。

（2）构造判断矩阵，决策者应该根据专家的意见结合现场情况以及疫情的严重性给出权系数。

（3）进行一致性检验。当CR＜0.1 时，通过一致性检验。

图1 层次分析结构

1.2 算例

判断矩阵由德尔菲法确定，本文以某一方舱医院的建设模式决策为例，给出决策背景及目标，采用德尔菲法对29 名相关领域专家进行调研，最终得到判断矩阵如下。

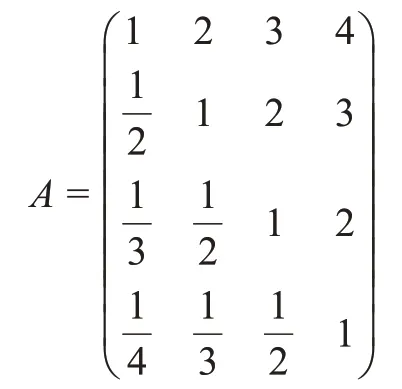
A的最大特征值为λ0= 4.03，相应的特征向量为

同理可以计算出改建和新建对于风险、时间、成本、可持续性的判断矩阵，

对应的最大特征值与特征向量依次为：

所以决策结果为选择新建方舱医院。

2 选址决策

2.1 选址决策因素

突发公共卫生事件方舱医院作为一种应急系统，除了要考虑应急系统常用的通行时间和距离因素外，还需增加建设工期因素和疫情防控因素，来全面考量选址决策问题。

（1）人口密集程度：突发公共卫生事件方舱医院收治大量具有传染性患者，因为既不能全部掌握其传播途径，又没有针对性的疫苗，方舱医院的选址应尽量避开人群密集的区域，以减少周围人群被感染的概率。

（2）远离重点运行区域：远离大型商业超市，重点保护文物，以及一些关切社会运行运转的城市配送中心或车站码头，食品加工企业或医疗物资生产转运中心等，以此防止可能的传染或污染，致使关键社会运营活动停摆。

（3）远离城市水源地：方舱医院生活用水，粪便排泄物，生活垃圾都有可能具有传染性，虽然医院对这些医疗和生活垃圾会进行集中处理与消毒，但也很容易对水源地造成污染。因此，方舱医院的选址要远离水源地或江河湖泊。

（4）处于下风区：对于能通过空气传播的疫情，病毒在空气中传播的速度取决于空气流通的速度，这时风向就显得尤为重要，如果方舱医院建在上风区，就会加速病毒在特定区域内传播速度，相反，方舱医院若处于下风区，就会对病毒的传播起到抑制的作用。

（5）较高地势：方舱医院应建在地势较高的地点，以避免因强降水而引起的洪水或泥石流。

（6）方舱医院的容量：方舱医院的容量要与现有患者数量以及未来可能增加患者的数量相匹配，宁可床等人不可人等床。

（7）负荷均衡程度：方舱医院要考虑收治效率，即每个方舱医院的负荷程度(实际人数/可容纳容量)要均衡，避免出现有的方舱医院床位不足，而有的方舱医院却有空床位的负荷不均衡情形，这样不仅浪费资源，还容易因患者二次转移而加大疫情扩散的几率[17]。

（8）基础设施完善程度：随着医院现代化水平的提高，医院不是独立功能单元，必须利用现场公共资源，依托水、电、通信、网络等基础设施，发挥应有的医治和隔离功能。基础设施完善能满足方舱医院能源供应、信息交流、医疗及生活保障的需要，其完善程度也影响着方舱医院建设和投入使用的时间。

（9）物资供应：不管是新建还是改建方舱医院，原材料供应是影响其工期的重要因素，原材料的及时供应能保证在工期内高质量完成建设。另外，医疗设备物资和生活物资供应连贯平稳程度，也是影响选址的重要因素[18]。

（10）建设工期：时间就是生命，新建和改建的工期是越短越好。征地或征建筑时间影响着投入的使用时间，征用后，不同类型场地都要建设成为符合应急医疗设施设计标准的医院，不同地址能否进驻大型设备，能否多工序同时作业，都会影响工程进度，必然对施工或改建工期有影响，从而影响整个建设工期长短。

（11）建设质量：新建和改建方舱医院的质量，不但影响收治效果，也会影响到医疗环境和生活环境，更会影响疫情防控效果，因此，能否使用先进诊疗设备会影响收治效果，能否有良好的医疗环境和生活环境也会影响治疗效果和防疫效果。

（12）建设成本：不同候选地址需要的建设成本不同，新建方舱医院时不同区域的土地成本不同，改建时不同场所租用的费用也不同，抗疫后恢复原样或改做他用成本也不同，因此方舱医院建设总成本影响着选址。

（13）运行成本：当方舱医院建设完成后，每天的医疗物资和生活物资运输成本，医疗废物处理成本，隔离防护成本，污废水处理成本等都影响着选址。

（14）最大通行时间：一个方舱医院服务一定半径内的所有患者，离方舱医院最远的患者到方舱医院的时间就是最大通行时间，因为患者的收治时间越短越好，在考虑交通条件和防护措施不理想条件下，最大通行时间是越短越好。

（15）平均通行时间：不仅需要最大通行时间最小，方舱医院服务半径内所有患者的平均通行时间也要尽可能的小。

（16）最大通行距离：离方舱医院最远的边缘区域到方舱医院的距离就是最大通行距离，距离越短患者就能尽早得到隔离和治疗，尤其是在交通工具不能应用情形下，该距离越短，患者能尽早收治，且疫情扩散的风险也越小。

（17）平均通行距离：不仅需要最大通行距离最短，方舱医院服务半径内所有区域内的患者的平均通行距离也要尽可能短，在道路中断受阻或救护车转运车等缺乏情况下，平均通行距离的长短更为重要。

2.2 目标规划模型建立

2.2.1 目标规划模型简介

目标规划数学模型的一般形式为

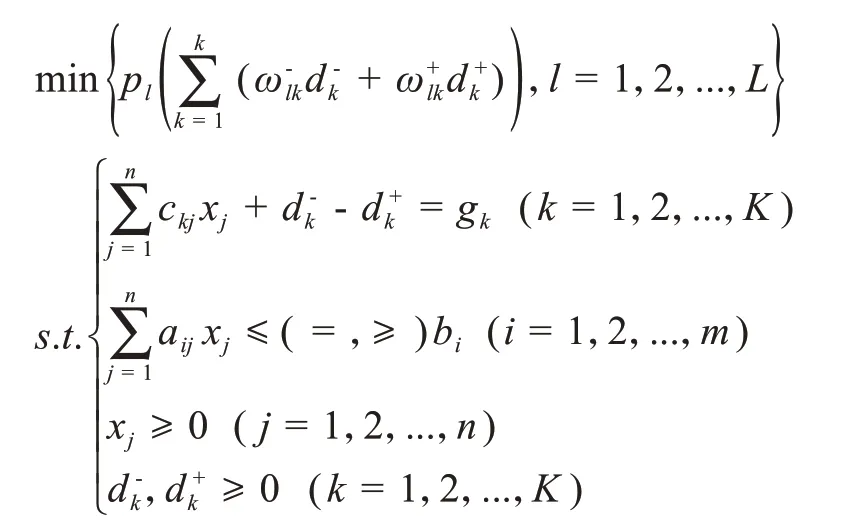
gk为第k 个约束的预期目标值，bi为绝对约束的目标值，pl为优先因子，ω-lk和ω+lk为pl优先因子对应各目标的权系数，dk-和dk+为决策变量的负、正偏差变量。

2.2.2 决策变量分析

方舱医院的选址决策模型包括两组决策变量[11]。第一组是候选地址的决策变量，假设N={1,2,3...,n}表示可能的候选地址的集合，对于每个候选中的地址都只有两种选择，即在该候选地址中建立方舱医院或者不在该地址中建立方舱医院。对于决策变量i来说，取xi= 0表示不在该候选地址中建立方舱医院，xi= 1 表示在该候选地址建立方舱医院，则第一组的决策变量可以表示为

第二组：假设M={1,2,3...,m}表示按照该城市的医院地理位置分布特点划分的应急区域集，对于某个具体的应急区域j决策变量yij表示在该区域j所发生的事故由第i应急服务设施进行应急的数目。则第二组所有的决策变量可以表达为yij(i∈N,j∈M)。

2.2.3 约束条件分析

（1）人口密集程度约束

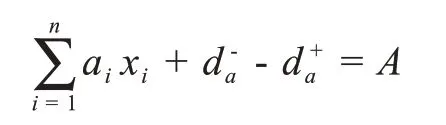
其中d+a，d-a表示人口密集程度约束条件的正负偏差变量，ai表示在地点i建立方舱医院其周围人口密集程度系数。A表示预计人口密集程度总系数。

（2）远离重点运行区域约束

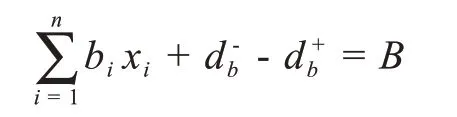
其中d+b，d-b表示方舱医院远离重点运行区域约束条件的正负偏差变量，bi表示在地点i建立方舱医院该方舱医院离重点运行区域的距离。B表示预计总距离。

（3）远离城市水源地约束

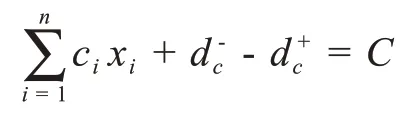
其中d+c，d-c表示离城市水源地约束条件的正负偏差变量，ci表示在地点i建立方舱医院该方舱医院离城市水源地的距离。C表示预计总距离。

（4）处于下风区约束

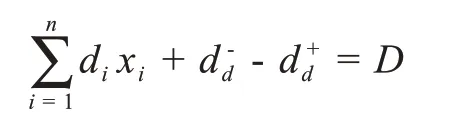
其中d+d，d-d表示方舱医院的位置处于下风区约束条件的正负偏差变量，di表示在地点i建立方舱医院其相对于下风区的偏差程度系数。D表示预计总偏差系数。

（5）较高地势约束

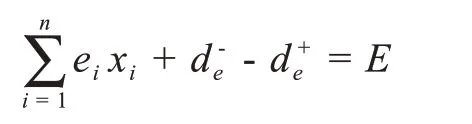
其中d+e，d-e表示方舱医院较高地势约束条件的正负偏差变量，ei表示在地点i建立方舱医院其地势高低程度系数。E表示预计总的地势高低程度系数。

（6）方舱医院的容量约束

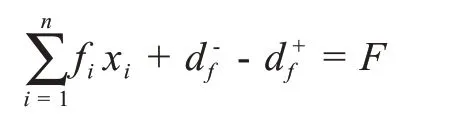
其中d+f，d-f表示方舱医院容量约束条件的正负偏差变量，fi表示在地点i建立方舱医院该方舱医院的容量。F表示预计方舱医院总容量。

（7）负荷均衡程度约束

其中gi，hj表示两个不同的方舱医院的供求比系数，dk+，dk-表示负荷均衡程度约束条件的正负偏差变量。

（8）基础设施完善程度约束

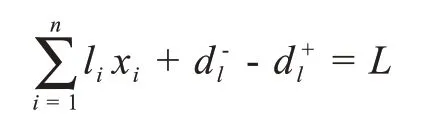
其中d+l，d-l表示基础设施完善程度约束条件的正负偏差变量，li表示在地点i建立方舱医院该地点基础设施完善程度系数。L表示预计总的基础设施完善程度系数。

（9）物资供应约束

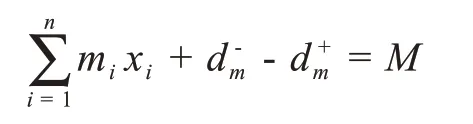
其中d+m，d-m表示物资供应约束条件的正负偏差变量，mi表示在地点i建立方舱医院该方舱医院离物资供应商平均距离。M表示预计总距离。

（10）建设工期约束

do+，do-表示建设工期约束条件的正负偏差变量，oi表示在地点i建立方舱医院的工期。O表示预计总工期。

（11）建设质量约束

dp+，dp-表示建设质量约束条件的正负偏差变量，pi表示在地点i建立方舱医院该医院的建设质量系数。P表示预计总质量系数。

（12）建设成本约束

dq+，dq-表示建设成本约束条件的正负偏差变量，qi表示在地点i建立方舱医院该医院的建设成本。Q表示预计总成本。

（13）运行成本约束

dr+，dr-表示运行成本约束条件的正负偏差变量，ri表示在地点i建立方舱医院该医院的运行成本。R表示预计总运行成本。

（14）最大通行时间约束

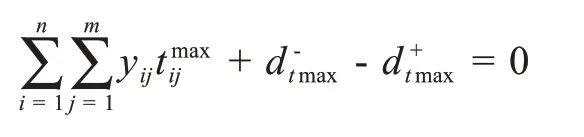
，表示最大通行时间约束条件的正负偏差变量，yij表示在该区域j所发生的事故由第i应急服务设施进行应急的数目。

（15）平均通行时间约束

（16）最大通行距离约束

（17）平均通行距离约束

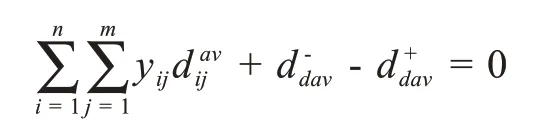
其中d+dav，d-dav表示平均通行距离约束条件的正负偏差变量，yij表示在该区域j所发生的事故由第i应急服务设施进行应急的数目。

根据以上分析构建出方舱医选址模型的目标函数

其中对于优先因子p，决策者可以根据具体情况和疫情的严重性确认，优先因子间的关系为pl＞＞pl+1，即pl对应的目标比pl+1对应的目标有绝对的优先性。

2.3 算例

2.3.1 数据来源

在决策者经过AHP方法进行选择后，决定进行新建方舱医院，现有6 个候选地址供决策者选择建立方舱医院，决策者要从6 个里面选出2 个地点建立方舱医院。本文以武汉方舱医院的选址为例，6个候选地址分别为1号东湖风景区，2 号武汉会展中心，3 号武汉国际博览中心，4 号武汉洪山体育馆，5 号石牌岭高级职业中学，6 号武汉体育中心。本算例中人口密集程度区域以小区为代表，重点运行区域以大型超市为代表，城市水源地以武汉市内的江河湖泊为代表，最大通行时间、最大通行距离以候选方舱医院所能覆盖到的最远小区到候选方舱医院的时间与距离表示，平均通行时间、平均通行距离以候选方舱医院覆盖到的所有小区到候选方舱医院的平均时间与平均距离表示。候选方舱医院容量：1 号东湖风景区1600 张床位，2 号武汉会展中心850 张床位，3 号武汉国际博览中心1000 张床位，4 号武汉洪山体育馆800张床位，5号石牌岭高级职业中学800张床位，6号武汉体育中心1000 张床位。其他约束条件涉及地理位置、基础设施、道路通行能力以百度地图的数据为依据，表1中的距离数据是中利用百度地图中的测距功能测得。（容量数据来源为网上整理https://card.weibo.com/article/m/show/id/2309404468939919851750? _wb_client_=1）

2.3.2 求解过程

对于语言变量，用模糊数表示。很高=0.9，高=0.7，一般=0.5，低=0.3，很低=0.1。对上述29 名专家，采用德尔菲法进行调研，最终得到各选址因素的优先因子和资源约束，如表1所示，x1,x2,x3,x4,x5,x6分别表示1 号武汉会展中心，2 号东湖风景区，3 号武汉国际博览中心，4 号武汉洪山体育馆，5 号石牌岭高级职业中学，6 号武汉体育中心，根据以上对语言变量的赋值，可以得到优化矩阵如下：

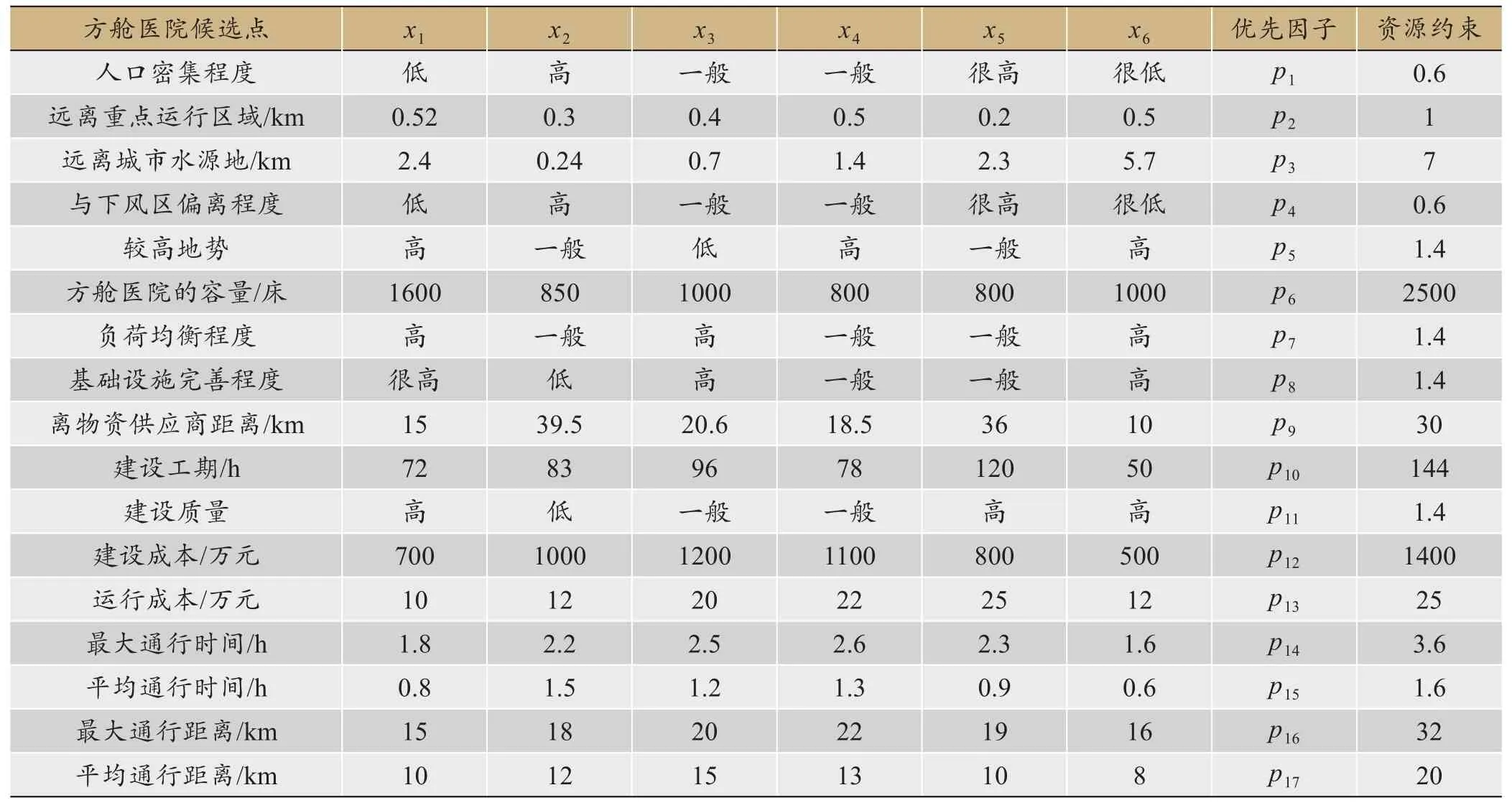
表1 候选方舱医院地址衡量指标汇总表

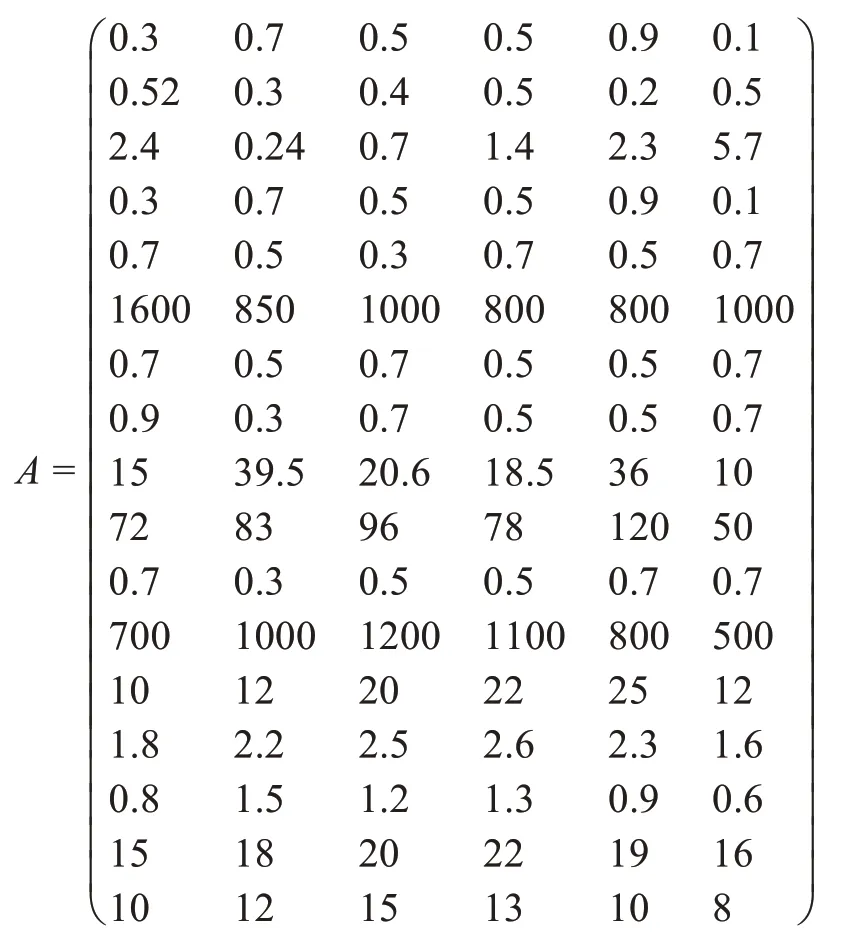
根据目标函数的优先因子和优化矩阵利用整数规划和线性规划的一般解法得到最优解x1= 1,x6= 1。即在1 号武汉会展中心和6 号武汉体育中心新建方舱医院。

3 结论及建议

本文在世界各国都建立方舱医院抗击突发公共卫生事件背景下，提出突发公共卫生事件方舱医院建设选址问题，首次提出两阶段决策方法，结合运用AHP 模型和目标规划模型来进行选址决策，为决策者提供了更多决策依据和决策空间，并且将建设工期和疫情防控两类主要因素引入到决策模型中，不仅有效地解决了方舱医院的选址问题，也为解决其他应急系统选址问题提供了新思路，如抗震救灾和野外战争的方舱医院选址等。研究发现：

两阶段决策方法能有效的解决突发公共卫生事件设施选址的问题。突发公共卫生事件由于其不可预测性和可能对公众健康造成严重损害的特点。政府部门应在事件发生后应立即采取补救措施以防止产生更大的危害，其中方舱医院的建立能有效的缓解医疗系统的压力，本文提出的两阶段选址决策方法在两阶段分别给出了建设模式的决策准则和选址约束条件，并且针对公共卫生事件的特点加入了建设工期和疫情防控约束，决策者可以根据决策准则和选址约束条件快速做出决策，可以避免事件进一步蔓延产生更大的危害。

两阶段决策方法能给决策者在突发事件中有更多的选择性。区别于传统的选址决策的一步到位的决策方法，两阶段决策能给予决策者更多的选择空间，首先可以根据突发事件的严重性选择改建还是新建，然后在对其进行选址决策。当面临重大公共卫生事件时，医疗系统急需方舱医院为其提供医疗支持时，可以选择改建模式节约建设时间，避免了传统决策方法从一开始就进行选址新建耗时久的缺点。

结合AHP 模型和目标规划模型的决策方法结合了定性和定量的分析，使模型的实用性增加了，并且优先因子的顺序可以人为的调整，加大了模型的适用性，进一步的对语言变量进行模糊数处理也有利于在实际决策中进行推广应用。

基于上述研究结论，本文提出以下建议：

1.对突发公共卫生事件方舱医院进行选址决策时，应重点考虑疫情防控因素。突发公共卫生事件方舱医院收治的都是具有高传染性的患者，选址时，备选地址需要符合对疫情防控的要求，如远离人群密集地区、远离水源等。

2.在突发公共卫生事件发生时，改建和新建方舱医院应同时进行。改建方舱医院收治的是症状较轻的患者而新建方舱医院收治的是重症患者，突发公共卫生事件发生时，不可避免的会同时出现轻症和重症患者，所以改建和新建方舱医院同时存在可以更有效的救治患者和减轻医疗系统的压力。

3.进行方舱医院建设模式决策时，应充分考虑建筑的可持续性。在公共卫生事件结束后，方舱医院将以什么形式继续存在是决策者在前期决策时要充分考虑的，改建方舱医院可以还原以前建筑的功能，而新建方舱医院在设计和建设时应该充分考虑公共卫生事件结束后发挥其他功能的作用，避免新建方舱医院出现闲置的现象。

本文通过实例结果可以得出，综合AHP和目标规划方法分两阶段进行决策是解决突发公共卫生事件方舱医院选址问题的一种有效方法。但为了简化模型，模型中引入的因素未能体现突发公共卫生事件方舱医院建设的全部特殊因素，未能综合考虑政治法律环境、建设施工人员供给程度、病毒传染途径、疫情防控等级和舱内功能设置等因素，后续研究可视实际情况需要进一步深入研究。