完美前向安全的基于身份认证密钥协商方案*

王 霏, 陈 明

宜春学院数学与计算机科学学院, 宜春336000

1 引言

认证密钥协商(authenticated key agreement, AKA) 协议广泛应用于两个用户或多个用户在开放网络环境下确认彼此身份、协商共享的会话密钥, 建立安全的通信信道.自Diffie 和Hellman[1]提出密钥交换概念以来, AKA 协议得到了广泛的研究和应用, 是保障互联网安全的基础协议之一.

基于身份密码 (identity-based cryptography, IBC) 由 Shamir[2]在 1984 年 CRYPTO 会议上首次提出, 核心思想是将用户身份 (ID) 嵌入其公钥中, 避免使用公钥证书.IBC 系统中, 可信的密钥生成中心 (private-key generator, PKG) 根据用户 ID 使用 PKG 主密钥为用户生成长期私钥, 用户公钥由PKG 公钥 + 用户 ID 组成, 不产生用户公钥证书, 去除了公钥证书的管理负担, 易于构建分布式的信任权威.IBC 体制可作为 PKI 体制的补充, 适合需要简单密钥管理结构的应用环境, 比如传感器网络等.自Boneh 等人[3]采用双线性对理论提出基于身份公钥加密方案以来, IBC 体制得到广泛研究.2007 年发布的 RFC5091[4]草案将 Boneh-Franklin(BF) 算法推荐为基于身份加密标准, 标志着 IBC 体制的标准化工作已经开始.

近年来, 基于身份的认证密钥交换 (ID-AKA) 方案也得到深入研究, 提出了许多有效和实用的方案[5–19].主要的研究成果采用类似 HMQV[20]协议的一轮 (one-round, 部分文献称为 two-message)隐式认证密钥交换结构, 而另一些研究者则提出通用的ID-AKA 构造方案.一轮ID-AKA 方案具有实现成本低、开销小等优点, 其安全性可直接规约到给定的困难数学问题和假设; 通用ID-AKA 方案的可扩展性和可移植性更好, 但其安全性往往取决于所使用的密码学原语.文献 [17]对最近提出的几种 ID-AKA方案进行了对比分析.不过, 截止目前, 大多数的 ID-AKA 方案在 CK[21]或 eCK 模型[22]下可证明安全, 仅实现了弱的完美前向安全性(weak perfect forward secrecy, wPFS).

一轮隐式认证密钥交换协议被认为无法实现完美前向安全性[20,22].最近, Cremers 等人[23,24]对一轮隐式认证密钥交换协议稍加扩展, 定义了两消息的AKA(记为DH-2) 协议类型, 提出一种适用于DH-2类型协议的通用变换(SIG 变换).SIG 变换采纳了通用构造的思想, 可实现密钥协商协议的模块化设计,将满足eCK 安全的DH-2 协议增强,实现完美前向安全性.文献[16]采用了Cremers 等人[23]的方法,提出了完美前向安全的ID-AKA 方案(下面记为Xie-ID-AKA).但是, 文献[24](见文献[24]定理1)特别指出SIG 变换需要使用强不可伪造(SUF-CMA[25])的签名算法.而Xie-ID-AKA 方案采用的Schnorr-like签名算法[26]不具有 SUF-CMA 安全性, 不满足 SIG 变换的要求, 并且文献[16]中没有采用 Cremers 等人[23,24]提出的安全模型对 Xie-ID-AKA 方案进行严格的安全性规约.因此, 本文认为 Xie-ID-AKA 方案不能实现完备的完美前向安全性.此外, Wang 等人[10]、Khatoon 等人[19]分别提出了完美前向安全的ID-AKA 方案 (分别记为Wang-ID-AKA、Khatoon-ID-AKA), 但是, 文献 [10,19]采用的安全模型与eCK 模型相近似, 仅模拟被动的 wPFS 敌手.事实上, Wang-ID-AKA 方案和 Khatoon-ID-AKA 方案仅实现了弱的完美前向安全性.就目前掌握的文献来看, 尚没有能够真正实现完美前向安全性的DH-2 类型ID-AKA 协议.

本文的主要工作:基于 Cremers 等人[24]的研究, 提出一种完美前向安全的 ID-AKA 方案 (下文中如未特别注明, 那么均指 DH-2 类型的 ID-AKA 协议), 主要内容分为以下三个方面.(1) 基于 Boneh 和Boyen[27]提出的强不可伪造的短签名方案(下文记为BBS), 提出强不可伪造的基于身份签名方案(记为ID-BBS), 并将ID-BBS 方案的安全性规约到BBS 方案的强不可伪造性.(2) 对Ni 等人[18]提出的eCK安全的 ID-AKA 方案进行简化以提高效率 (简化后的方案记为 sN-ID-AKA), 结合 ID-BBS 方案, 采用SIG 变换方法, 将sN-ID-AKA 方案转化为实现eCK-PFS[24]安全的ID-AKA 方案.(3) 结合eCK-PFS模型和ID-eCK 模型[17,28], 定义了ID-AKA 方案分析的强安全模型ID-eCK-PFS, 并将本文提出方案的安全性规约到ID-BBS 方案的强不可伪造性、以及sN-ID-AKA 方案的ID-eCK 安全性.此外, 本文对比分析了eCK-PFS 模型和eCK 模型的主要区别, 明确了eCK-PFS 模型更强安全性的优势所在.

2 背景知识

2.1 困难数学问题与假设

这里简要阐述双线性映射理论, 及存在的困难数学问题和假设, 详细内容请参考文献[18,27].

双线性映射:给定大素数p, 令G1, G2, GT是阶为 p 的乘法循环群, 令g1, g2分别是群G1, G2的生成元; 假设存在同构函数 ψ: G2→G1使得 ψ(g2)=g1成立.如果映射 e:G1×G2→GT是从 G1×G2到GT的一个有效的双线性映射, 则满足如下性质.

(1) 双线性: 给定 u ∈ G1, v ∈ G2和任意的 a, b ∈ Zp, 满足 e(ua,vb)=e(u,v)ab;

(2) 非退化性: e(g1,g2)1;

(3) 可计算性: 给定任意的u ∈G1, v ∈G2, 存在多项式时间算法能成功计算e(u,v).

CDH (computational Diffie–Hellman) 问题:对于任意未知的 a,b ∈ Zp, 给定求解其中, i ∈{1,2}.

CDH 假设:如果不存在多项式时间算法在时间 t 内以至少 ϵ 的概率求解 CDH 问题, 那么称 (ϵ,t)-CDH 假设成立.

q-SDH(q-Strong Diffie-Hellman) 问题:给定 q+2 个元素的元组且存在同构函数 ψ(g2)=g1, 计算输出其中, c ∈Zp.

q-SDH 假设:如果不存在多项式时间算法在时间 t 内以至少ϵ 的概率求解 q-SDH 问题, 那么称(q,ϵ, t)-SDH 假设成立.

说明: 为了叙述简洁, 本文省略了 “mod p” 运算.

2.2 ID-AKA协议及其安全模型

2.2.1 ID-AKA 协议定义

ID-AKA 协议包含系统设置、密钥生成和密钥协商三个算法.

系统设置: 输入安全参数, PKG 产生主密钥和公开的系统参数.

密钥生成: 输入用户身份, PKG 产生基于用户身份的长期认证密钥, 通过安全信道返回给用户.

密钥协商: 期望建立安全信道的两个用户之间通过公开信道完成交互式协议, 相互认证彼此身份, 交换会话密钥材料, 建立共享的会话密钥.

2.2.2 ID-AKA 协议安全模型定义

基于文献 [17,24,28]的工作, 本文将 eCK-PFS 模型扩展到 ID-AKA 协议分析领域, 记为 ID-eCKPFS 模型.

令 P = {ID1,ID2,··· ,IDN} 表示包含 N 个诚实用户的有限集合, IDi为用户身份标识, i ∈{1,··· ,N}.

会话(Session): 协议实例的一次运行被称为一个会话.每一个会话 s 由一个确定的六元组Ts唯一标识, Ts= (sactor,speer,srole,ssent,srecv,scomp).其中, sactor,speer表示会话拥有者及会话对端实体的ID;srole表示会话拥有者在当前会话中的角色, 要么是一个发起者 (用 I 表示), 或者是一个响应者 (用 R 表示); ssent,srecv表示会话发送和接收的消息, scomp表示会话 s 是否已完成, scomp= T 表示会话已完成,否则 scomp=⊥ 表示会话未完成(“⊥” 表示为空, 下同).

敌手(Adversary): 敌手被模拟为一个概率多项式时间图灵机, 允许执行多项式有界(次) 的询问.

Send(s, M) 询问: Send 询问模拟敌手发送消息 M 到会话 s.模拟器根据协议规范返回相应的应答,然后更新Ts中的相应内容.特定地, 敌手通过发起Send(s, IDj) 询问和 Send(s, IDj, M) 询问分别创建发起者会话和响应者会话, 并且假定speer=IDj.

Corrupt(ID) 询问: 如果ID ∈P, 模拟器输出用户 ID 的长期私钥, 否则返回 ⊥.

Ephemeral-key(s) 询问: 如果 s 存在, 那么返回该会话的临时秘密.

Session-key(s) 询问: 如果 s 存在, 且已完成(scomp=T), 则返回该会话的会话密钥.

Test(s∗) 询问: 模拟器随机选择 b ∈ (0,1), 如果 b = 0, 输出随机的 SK ←{0,1}κ, 否则输出 s∗的会话密钥.其中, κ 为安全参数.Test 询问仅执行一次, 且要求s∗是已完成的新鲜会话, 并且在整个模拟过程中不能破坏s∗的新鲜性, 否则模拟失败.

下面定义原始会话、匹配会话和会话新鲜性.

定义 1 (Origin-session)如果会话 s′(可能尚未完成) 与已完成的会话 s 满足:那么s′是 s 的原始会话, 用关系 s′→ s 表示.

定义 2 (Matching-session)如果两个已完成的会话 s 与 s′满足:那么 s 与 s′互为匹配会话, 用关系 s ↔s′表示.

注意, 匹配会话是相互的, 即关系 s ↔ s′和 s′↔ s 同时成立; 而原始会话是单向的, 即关系 s′→ s和 s → s′不一定同时成立.

定义 3 (ID-eCK-PFSfresh)如果已完成的会话s 满足如下条件, 那么 s 满足ID-eCK-PFSfresh.

(1) sactor,speer是诚实的参与者;

(2) 未执行过Session-key(s) 询问;

(3) 如果存在 s∗↔s, 则未执行过 Session-key (s∗) 询问;

(4) 不允许同时执行 Ephemeral-key(s) 询问和 Corrupt(sactor) 询问;

(5) 对于所有的 s′→ s, 不允许同时执行 Corrupt(speer) 询问和 Ephemeral-key(s′) 询问;

(6) 如果不存在 s′满足 s′→ s, 那么在 s 完成之前, 不允许执行 Corrupt(speer) 询问.

安全游戏 (Security Game): 安全游戏被模拟为挑战者 C 与敌手 A 之间的一系列测试游戏 Game.游戏分为初始化、询问和挑战三个阶段.初始化阶段, 输入安全参数κ, C 创建系统参数和用户密钥, 并将所有公开参数发送给A.询问阶段, A 自适应地执行多项式时间有界(次) 的询问, 但仅能提交1 次对挑战会话 s∗的 Test(s∗) 询问, C 模拟协议的相应算法做出应答, 在询问结束后, s∗仍然满足新鲜性定义.挑战阶段, A 输出对 Test(s∗) 询问中 b 的猜测 b′∈ {0,1}.如果 b′= b, A 赢得游戏.A 赢得游戏的优势定义为

定义 4如果 DH-2 类型的 ID-AKA 协议满足如下条件, 被认为满足 ID-eCK-PFS 安全: 1) 如果两个诚实的参与者完成了一次匹配的会话, 那么他们必然以极大的概率计算得到相同的会话密钥; 2) 对任意多项式时间敌手是可忽略的.

2.2.3 eCK-PFS 模型与eCK 模型前向安全性比较

下面首先回顾eCK 模型的新鲜性定义, 原定义请参考文献[22]的定义2 和定义3.

定义 5[eCKfresh]如果已完成的会话 s 满足如下条件, 那么s 满足eCKfresh.

(1) sactor,speer是诚实的参与者;

(2) 未执行过 Session-key(s) 询问和 Session-key(s′) 询问 (如果 s′↔ s 存在);

(3) 如果存在 s′↔ s , 则,

- 不允许同时执行Ephemeral-key(s) 询问和 Corrupt(sactor) 询问;

- 不允许同时执行Ephemeral-key(s′) 询问和 Corrupt(speer) 询问.

(4) 如果不存在 s′↔ s , 则,

- 不允许同时执行Ephemeral-key(s) 询问和 Corrupt(sactor) 询问;

- 在s 完成以前, 不允许执行Corrupt(speer) 询问; 特定地, 对于一轮密钥交换协议, 任何时候均不允许执行Corrupt(speer) 询问 (参考文献 [22]的定义 3).

在 eCK 模型中, 未定义原始会话.与匹配会话不同, 原始会话能区分重放消息, 强调会话消息的来源, 即一个会话的输出等于另一会话的输入.事实上, 匹配会话是原始会话的子集.表1 对 eCK 模型和eCK-PFS 模型中前向安全性进行了对比, 其它安全性, 如密钥泄露伪装(KCI) 攻击等, 两类模型等效.其中, S1–S4 和 S1′–S2′表示安全模型能模拟的攻击场景, TS, MS, OS 分别表示 Test 会话、匹配会话和原始会话, sk 和ek 分别表示会话拥有者的长期私钥和临时私钥, ek 值等于 n 表示对应的会话不存在, r 表示允许敌手询问相应私钥, r∗表示允许敌手在会话完成之后询问相应私钥, ok 表示不允许敌手询问相应私钥, /表示eCK 模型未定义OS, √表示安全模型能模拟对应的攻击场景, × 则表示不能模拟, Θ 表示该场景在eCK 模型中存在等效的情况.

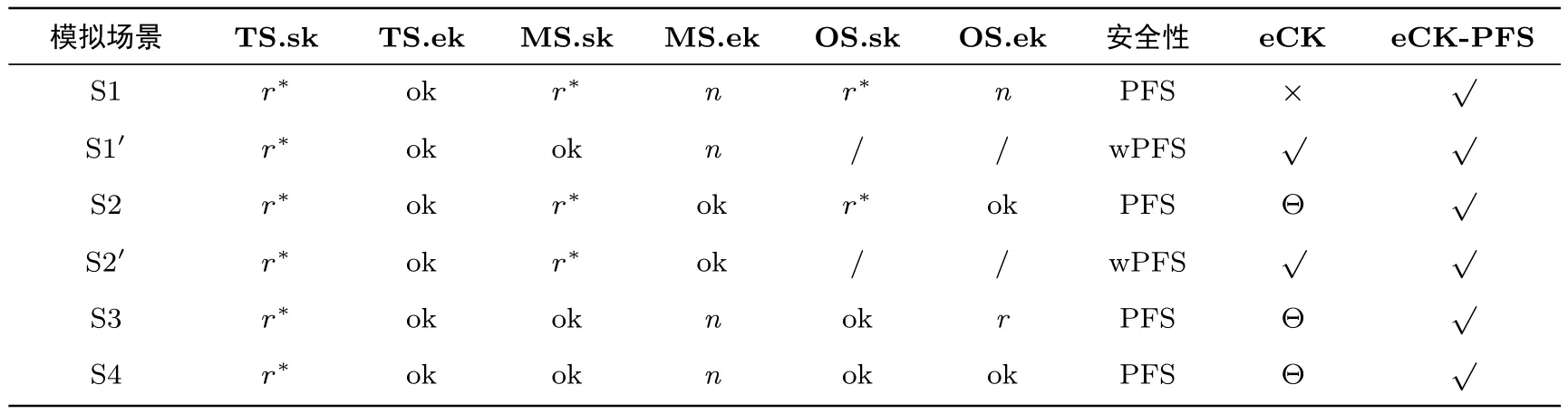
表1 eCK 模型与eCK-PFS 模型前向安全性对比Table 1 Comparison of forward secrecy between eCK model and eCK-PFS model

从表1 可以看出, eCK 模型不能模拟场景 S1.场景 S1′描述了在 eCK 模型下 Test 会话不存在匹配会话时的情形, 事实上 S1′包含了存在原始会话 (场景 S3 和 S4) 或不存在 (场景 S1) 两种情形, 但是, 由于eCK 模型未定义原始会话, 因此不区分这两种情形, 均不允许敌手询问Test 会话中对端实体的sk (见定义5 第 (4) 条对一轮密钥协议的补充定义)(注意: 根据定义, Test 会话的对端实体等于其匹配会话 (可能并不存在) 的拥有者).也就是说, 从敌手的视角来看, 场景 S1′与 S3 和 S4 等效, 而不包含 S1 (或者说, 在场景 S1 中, eCK 模型按照与 S3 和 S4 相同的方式处理).在场景 S1 中, eCK-PFS 模型允许敌手在 Test 会话完成以后询问参与双方实体的sk, 实现了模拟强的 PFS 安全性.此外, 从敌手的视角来看,场景 S2 与 S2′等效.

3 完美前向安全的ID-AKA方案

本文方案的提出分为两步: 首先, 将 Boneh 和 Boyen[27]提出的强不可伪造的短签名方案 (BBS 方案) 改造为强不可伪造的基于身份签名方案(ID-BBS 方案); 第二步, 在N-ID-AKA 方案的基础上提出更为简洁高效的 sN-ID-AKA 方案, 然后采用 SIG 变换, 将其转化为实现 eCK-PFS 安全的 ID-AKA 方案.

3.1 强不可伪造的基于身份签名

下面简要描述BBS 方案.

给定签名者的公私钥对: PK=(g1,g2,u,v,z),SK=(x,y).其中, g1和 g2分别是群 G1和 G2的生成元,

BBS 签名: 输入待签名消息 m ∈ Zp和用户私钥 SK = (x,y), 随机选择 r ∈ Zp, 计算输出签名 (σ,r).

BBS 签名验证: 收到消息 m 的签名 (σ,r), 输入用户公钥 PK = (g1,g2,u,v,z), 验证等式是否成立, 若等式成立则接受签名, 否则拒绝签名.

文献 [27]证明了, 在 SUF-CMA 模型下, 如果 q-SDH 假设成立, 则 BBS 方案满足强的不可伪造性.

SUF-CMA 是对 EUF-CMA 的增强, 是指在 EUF-CMA 安全性基础上, 即使敌手获得用户 Alice 对消息 m 的合法签名 σ, 也不能伪造 Alice 对消息 m 的新的签名 σ∗σ.而 EUF-CMA 模型则不能模拟该场景.

本文改造的ID-BBS 方案包括: 系统建立、密钥生成、签名和签名验证四个算法.

系统建立: 输入安全参数 κ, PKG 产生系统公开参数 param = (G1,G2,GT,g1,g2,e,z,P0,H1,H2,H3), 其中, e:G1×G2→GT为满足条件的双线性映射, z =e(g1,g2), P0=为 PKG 的公钥, s ∈Zp为 PKG 的主密钥, H1: {0,1}ID×G2→ Zp, H2: {0,1}ID×G2→ Zp和 H3: G2→ Zp为密码 Hash函数.

密钥生成: 提交用户身份ID,PKG 随机选择r1,r2∈Zp,计算q2=H2(ID,R2), x=r1+sq1,y =r2+sq2, 输出用户私钥则用户公钥PK=(u,v,z).

ID-BBS 签名 (SignID-BBS): 输入待签名消息 m ∈G2和用户私钥 SK=(x,y), 随机选择 r ∈Zp, 计算输出签名 (σ,r).由于本文密钥交换方案中需要对 G2中的成员进行签名, 而 BBS 签名算法仅能对Zp中成员进行签名, 因此, 我们引入 Hash 函数H3.

ID-BBS 签名验证 (VerifyID-BBS): 收到消息 m 的签名 (σ,r), 输入用户公钥 PK = (u,v,z), 计算m′=H3(m), 验证等式是否成立, 若等式成立则接受签名, 否则拒绝签名.

3.1.1 ID-BBS 方案安全性分析

本文将 ID-BBS 方案的不可伪造性规约到BBS 方案的不可伪造性, 即, 如果存在敌手在多项式时间内成功伪造一个有效的ID-BBS 的签名, 则模拟器能输出一个有效的伪造BBS 签名.规约过程简要描述如下.

定理 1如果群 G1,G2,GT上的 q-SDH 假设成立, 且如果 BBS 签名具有强不可伪造性, 那么, IDBBS 签名方案实现了强不可伪造性.

证明:安全性规约过程分为初始化、询问和伪造三个阶段, 包含两类模拟器B0和B1, 以及敌手A.规约形式采用嵌套的游戏模拟方式, 外层模拟 (ID-BBS 游戏, 采用了Paterson 等人[29]提出的选择身份安全模型) 以B0模拟器, A 为敌手, 内层模拟(BBS 游戏, 本文不详细描述, 参考文献[27]) 以 B1为模拟器, B0为敌手.

初始化: 输入安全参数 κ, 模拟器 B0作为 BBS 游戏的敌手从挑战者 B1处取得用于 BBS 挑战的公开参数 (G1,G2,GT,g1,g2,e,u,v,z), 然后产生 ID-BBS 系统公开参数 param = (G1,G2,GT,g1,g2,e,z,P0,H1,H2,H3).其中, H1,H2模拟为随机预言机 (ID-BBS 方案采用了与文献 [18]相同的基于身份密钥生成算法, 采用Schnorr 签名[30]生成用户私钥, 而Schnorr 签名是随机预言模型下的签名方案, 因此外层模拟使用了随机预言机), 其它参数如上所述.为了实现模拟过程的一致性, B0维护初始为空的列表L1= (ID,R1,h1),L2= (ID,R2,h2) 和LID分别记录H1,H2询问和用户密钥, 对同一询问做出相同的应答.

询问: A 自适应地提交多项式时间的下列询问.

H1询问: 提交 (ID,R1) 询问, 若 (ID,R1,h1) 在 L1中已存在, 则返回 h1, 否则随机选择 h1∈Zp,并返回给 A, 然后将 (ID,R1,h1) 插入 L1中.

H2询问: 提交 (ID,R2) 询问, 若 (ID,R2,h2) 在 L2中已存在, 则返回 h2, 否则随机选择 h2∈Zp,并返回给 A, 然后将 (ID,R2,h2) 插入 L2中.

密钥询问: 敌手 A 提交用户身份 IDi, 若 IDi= IDI, 则 B0终止模拟, 模拟失败; 否则按照 IDBBS 方案的密钥生成算法产生 IDi的私钥并发送给 A, 然后将用户密钥信息插入 LID.注意, 密钥生成算法中对哈希函数 H1,H2的计算用 H1,H2询问代替; IDI是 B0选定的挑战用户, 设置其公钥为(g1,g2,RI1,RI2,u,v,z), 对 B0来说, 其私钥未知, 其中,通过H1,H2询问取得, (u,v,z) 来自 B1.

签名询问: A 提交 (IDi,m) 的签名询问.若 IDi= IDI, B0计算 m′= H3(m), 提交 BBS 游戏的签名询问, 将得到的签名结果直接输出给 A; 否则, 通过密钥询问取得 IDi的私钥, 按照 ID-BBS 签名算法计算签名并返回给A.

伪造: 最后, A 提交对 ID-BBS 签名的伪造签名 (ID∗,m∗,σ∗,r∗).如果 ID∗IDI, 则模拟失败, 否则, B0计算 m∗∗=H3(m∗), 提交 (m∗∗,σ∗,r∗) 作为对 BBS 游戏的伪造结果.

模拟过程到此结束.显然, 如果 A 成功伪造 ID-BBS 签名, 则 B0也能成功伪造 BBS 签名.令 A 成功的概率为 ϵ, 那么 B0成功的概率为 f(ϵ), 其中, f(∗) 为多项式函数.

3.2 完美前向安全的ID-AKA方案

本节首先对 N-ID-AKA 方案进行简化, 提出 sN-ID-AKA 方案, 然后, 整合 ID-BBS 签名, 提出强安全的 eN-ID-AKA 方案.由于N-ID-AKA 方案采用了椭圆曲线上的加法群, 为了实现与 ID-BBS 方案整合, 本文采用与ID-BBS 方案一致的乘法群.尽管采用了不同的群, 但是两类群具有相似的性质, 即, CDH假设在两类群中都成立.sN-ID-AKA 方案描述如下.

系统设置: 输入安全参数 κ, PKG 产生并输出系统参数 param = (G,g,P0,H1,H).其中, G 为素数阶 p 的乘法循环群, g 为群 G 的生成元, P0= gs为 PKG 的公钥, s ∈ Zp为 PKG 的主密钥,H1:{0,1}ID×G →Zp将身份ID 映射到Zp中的一个随机成员, H :{0,1}∗→(0,1)κ为密钥导出函数.

密钥生成: 提交用户身份IDi,PKG 随机选择ri∈Zp,计算Ri=gri,qi=H1(IDi,Ri),xi=ri+sqi,输出用户私钥ski=(xi,Ri); 令ui=gxi, 则用户公钥pki=ui.

密钥协商: Alice 和Bob 期望建立安全通信信道, 按照以下步骤进行密钥协商.

(1) Alice 随机选择临时私钥 tA∈Zp, 计算临时公钥 TA=gtA, 发送 (IDA,RA,TA) 给 Bob; Bob 随机选择临时私钥 tB∈Zp, 计算临时公钥 TB=gtB, 发送 (IDB,RB,TB) 给 Alice.

(2) 收到 (IDA,RA,TA) 后, Bob 计算计算会话密钥skBA=H(IDA,IDB,TA,TB,KB).

(3) 收到 (IDB,RB,TB) 后, Alice 计算计算会话密钥skAB=H(IDA,IDB,TA,TB,KA).

容易验证skAB=skBA, Alice 和Bob 计算得到相同的会话密钥, 实现了相互的隐式认证和密钥协商.

eN-ID-AKA 方案描述如下.

系统设置: 输入安全参数 κ, PKG 产生并输出系统参数 param = (G1,G2,GT,g1,g2,e,z,P0,H1,H2,H3,H).其中, (G1,G2,GT,g1,g2,e,z,P0,H1,H2,H3) 与 ID-BBS 方案一致, H 为密钥导出函数.

密钥生成: 与 sN-ID-AKA 方案和 ID-BBS 方案基本相同, 用户 IDi的私钥为: ski= (xi1,xi2,yi,Ri1,Ri2,Ri3),pki=(ui1,ui2,vi).其中,xi1=ri1+sqi1, xi2=ri2+sqi2, yi=ri3+sqi3, qi1=H1(IDi,Ri1), qi2=H2(IDi,Ri2), qi3=H1(IDi,Ri3),说明: 本文采用独立的两组密钥分别用于认证和签名以增强安全性, (xi1,Ri1,ui1) 用于认证,(xi2,yi,Ri2,Ri3,ui2,vi) 用于签名.

密钥协商: Alice 和Bob 按照以下步骤进行密钥协商.

(1) 与 sN-ID-AKA 方案步骤 (1) 基本相同, 其中,此外, Alice 计算对 TA的签名 σA=SignID-BBS(param,xA2,yA,TA) 发送 (IDA,RA1,RA2,RA3,TA,σA) 给 Bob; Bob 计算对 TB的签名 σB= SignID-BBS(param,xB2,yB,TB) 发送 (IDB,RB1,RB2,RB3,TB,σB) 给Alice.

(2) 收到(IDA,RA1,RA2,RA3,TA,σA)后,Bob 首先验证签名σA,若签名有效则按照与sN-ID-AKA方案步骤(2) 相同的方法计算会话密钥skBA.

(3) 收到 (IDB,RB1,RB2,RB3,TB,σB) 后, Alice 首先验证签名 σB, 若签名有效则按照与 sN-IDAKA 方案步骤(3) 相同的方法计算会话密钥skAB.

eN-ID-AKA 方案密钥协商过程如图1.

4 分析与比较

4.1 eN-ID-AKA方案安全性分析

首先, 本节采用 ID-eCK 模型[17,28]对 sN-ID-AKA 方案进行安全性规约, 然后采用第 2 节描述的ID-eCK-PFS 模型对eN-ID-AKA 方案进行安全性规约.参照文献 [24]的定理1, 本文将eN-ID-AKA 方案的ID-eCK-PFS 安全性规约到sN-ID-AKA 方案的ID-eCK 安全性, 即, 如果存在敌手以不可忽略的概率攻破eN-ID-AKA 方案的ID-eCK-PFS 安全性, 那么必然存在敌手以不可忽略的优势攻破sN-ID-AKA方案的eCK 安全性.

定理 2如果乘法循环群 G 上的 CDH 假设成立, 那么 sN-ID-AKA 方案满足 ID-eCK 安全.

证明:给定 CDH 问题实例g,ga,gb∈G, 下面演示模拟器 C 利用敌手 A 求解 CDH 问题.令π 表示 sN-ID-AKA 方案, Si表示游戏 Game i 中敌手对 Test 会话猜测成功事件, 那么 Game i 中敌手成功的优势: ϵi=|2P(Si)−1|.令N,qs分别表示游戏中创建的用户数和会话数的上界.

图1 完美前向安全的ID-AKA 方案Figure 1 An ID-AKA scheme with PFS

Game 0.Game 0 模拟 A 与 C 之间的游戏, A 根据 ID-eCK 模型自适应地提交询问, C 按照协议 π对 A 的询问做出应答.则 Game 0 中 A 成功的优势定义为 ϵ0.

Game 1.在Game 0 的基础上, Game 1 考虑一些小概率的碰撞事件, 比如在不同的会话中发生临时私钥碰撞事件等, 当出现此类事件则终止模拟, 模拟失败.令Collπ表示上述小概率事件, 那么根据差分引理 (文献 [24]的 Lemma 1), 有: |P(S0)− P(S1)|≤ P(Collπ), 进而可推导 ϵ0≤ ϵ1+P(Collπ), 推导过程同文献 [24]定理 1.

Game 2.在Game 1 的基础上, Game 2 考虑一类较大概率的失败事件E1.模拟开始之前, C 随机选择 l ∈ {1,2,··· ,qs},ID∗∈ {ID1,ID2,··· ,IDN}, 令 s∗表示游戏中的第 l 个会话, 并且期望敌手 A 发起会话 s∗的 Test(s∗) 询问,且令 E1表示 A 发起了 Test(s′) 询问,并且如果事件 E1发生, 则终止模拟过程, 敌手 A 输出随机的 b ∈(0,1).如果事件 E1不发生, 则 A 成功的概率与 Game 1 相同, 即:如果事件 E1发生, 则 P(S2|E1) = 1/2.那么:由此可推导:

Game 3.在 Game 2 的基础上, Game 3 引入随机预言机 OH1, OH分别模拟密码哈希函数 H1,H.输入安全参数κ, C 产生公开参数param=(G,g,P0), 维护初始为空的列表LID, LSK.其中, P0=ga.

(1) A 提交 OH1询问．如果 ID 在 LID中存在, 则输出 qID, 否则 C 随机选择并输出 qID∈Zp; 如果 ID = ID∗, C 随机选择 rID∈ Zp, 计算 RID= grID, 将 (ID,RID,rID,⊥,qID) 插入 LID; 否则C 随机选择 xID∈Zp, 计算将 (ID,RID,⊥,xID,qID) 插入 LID．

(2) A 提交OH询问．如果 (IDi,IDj,Ti,Tj,K,SK) 在 LSK中存在, 则输出SK; 否则随机选择并输出 SK ∈(0,1)κ．然后将 (IDi,IDj,Ti,Tj,K,SK) 插入 LSK.

(3) A 提交 Corrupt(ID) 询问.如果 ID = ID∗, 则终止游戏, 模拟失败; 否则, 如果 ID 在 LID中存在, 则输出 xID, 如果 ID 在 LID中不存在, 则通过 OH1询问创建并返回私钥 xID.

(4) A 提交 Ephemeral-key(s) 询问.如果 s = s∗则终止游戏, 模拟失败; 如果会话 s 已建立临时密钥, 则返回 s 的临时密钥, 否则返回 ⊥.

(5) A 提交 Session-key(s) 询问, 如果 s = s∗∨s ↔ s∗则终止游戏, 模拟失败; 如果 scompT,则返回 ⊥; 如果 (IDi,IDj,Ti,Tj,K,SK) 在 LSK中存在, 则输出 SK; 否则, 随机选择并输出SK ∈{0,1}κ．其中, IDi,IDj为会话 s 中参与者身份, Ti,Tj是 s 中发送和接收的消息.

(6) A 提交 Send(s) 询问, C 按照下列方式作出应答.假设sactor=IDi.

- 如果 A 提交 Send(s,IDj) 询问以激活发起者会话 s.如果 s = s∗则令 Ti= gb, 否则 C 随机选择 ti∈Zp, 计算 Ti=gti, 输出 (IDi,Ri,Ti).

- 如果A 提交Send(s,IDj,M) 询问以激活响应者会话 s.如果s=s∗则令Ti=gb, 否则C 随机选择 ti∈ Zp, 计算 Ti=gti, 输出 (IDi,Ri,Ti), 设置 scomp=T.

- 如果 A 提交 Send(s, M) 询问.此时, s 是一个已激活的会话, 则接受该会话, 设置scomp=T.

(7) A 提交 Test(s∗) 询问, C 随机选择 SK ∈ {0,1}κ, 并返回给 A.

(8) 最后, A 输出其猜测 b′∈ (0,1).

如果 A 猜测成功, 则 LSK中必然存在 (IDi,IDj,Ti,Tj,K∗) 与 s∗匹配.如果 s∗为发起者会话, 那么 C 计算否则 s∗为响应者会话, 则计算 gab=作为对CDH 实例的回答.

从模拟过程可以看出, 如果 A 成功, 则 C 也成功.令 A 成功的优势定义为 ϵ3, 令 C 成功的概率为则那么:

Game 3 模拟了 ID-eCK 模型中的抗密钥泄露伪装 (KCI) 安全性, 而wPFS 安全性和抗临时密钥泄露(ESR) 安全性与此类似, 限于论文篇幅, 本文不再详细论述, 相关内容可参考文献[17,28].

定理 3如果群G1, G2, GT上的CDH 假设和 q-SDH 假设成立, 且如果ID-BBS 签名具有强不可伪造性、sN-ID-AKA 方案满足 ID-eCK 安全, 那么 eN-ID-AKA 方案实现了 ID-eCK-PFS 安全.

证明:令π 表示sN-ID-AKA 方案, SIG(π) 表示本文提出的eN-ID-AKA 方案, Si表示游戏Game i 中敌手对Test 会话猜测成功事件, 那么Game i 中敌手成功的优势: ϵi=|2P(Si)−1|.令N,qs分别表示游戏中创建的用户数和会话数的上界.

Game 0.Game 0 模拟多项式时间敌手 A 与模拟器 C 之间的游戏, 敌手 A 根据 2.2.2 节定义的ID-eCK-PFS 模型自适应地提交询问, C 按照协议 SIG(π) 对 A 的询问做出应答.则 Game 0 中 A 成功的优势定义为ϵ0.

Game 1.在Game 0 的基础上, Game 1 考虑一些小概率的碰撞事件, 比如在不同的会话中发生临时私钥碰撞事件等, 当出现此类事件则终止模拟, 模拟失败.令CollSIG(π)表示上述小概率事件, 那么根据差分引理[24], 有: |P(S0)− P(S1)|≤ P(CollSIG(π)), 同定理 2, 可推导 ϵ0≤ ϵ1+P(CollSIG(π)).

Game 2.在 Game 1 的基础上, Game 2 考虑一类较大概率的失败事件 E1.与定理 2 的 Game 2 相同, 可推导:

Game 3.在Game 2 的基础上, Game 3 考虑对ID-BBS 签名的伪造事件E2.除非事件E2发生, 否则 Game 3 与 Game 2 相同.如果事件 E2发生, 那么敌手 A 输出随机的 b ∈(0,1).根据差分引理[24],有: |P(S2)−P(S3)|≤P(E2).

引理 1如果 ID-BBS 签名具有强不可伪造性, 那么,是可忽略的.其中,表示算法 F 成功伪造 ID-BBS 签名的概率.

证明:考虑如下算法 F, 以敌手A 作为子模块.给定N 个用户, 并随机选择一个挑战用户身份ID∗,F 可以访问签名预言机 OID-BBS取得 ID∗的签名 (OID-BBS构造方式参考 3.1.1 节的 ID-BBS 游戏), 并从 OID-BBS获得对 ID-BBS 签名的挑战; F 构造系统公开参数 param 和 ID∗的长期认证密钥、以及除ID∗以外的其他用户密钥, 算法描述如下.注意, ID∗的签名验证公钥从OID-BBS取得, 对应的签名私钥未知.

(1) 输入安全参数κ, 运行子算法A, 将公开参数param 以及N 个用户的身份和公钥发送给A.

(2) A 提交Send(s,IDj) 询问以激活发起者会话 s.此时, speer=IDj, F 按以下方式进行应答.

- 如果sactor=IDiID∗, 那么按照协议步骤计算响应消息(IDi,Ri1,Ri2,Ri3,Ti,σi)发送给A.

- 如果 sactor= ID∗, 那么首先按照协议计算 T∗, 然后访问预言机 OID-BBS取得 ID∗对 T∗的签名 σ∗, 并将响应消息发送给A.F 将记录(ID∗,T∗,σ∗) 插入初始为空的列表 L.

(3) A 提交Send(s,IDj,M) 询问以激活响应者会话 s.F 首先验证消息 M 是否符合协议规范, 以及M 是否包含IDj的合法签名; 如果验证不成功, 则返回⊥, 否则按以下方式进行应答.

- 如果sactor=IDiID∗, 那么按照协议步骤计算响应消息(IDi,Ri1,Ri2,Ri3,Ti,σi)发送给A.

- 如果 sactor=ID∗, 那么首先按照协议计算 T∗, 然后访问预言机 OID-BBS取得 ID∗对 T∗的签名σ∗, 并将响应消息发送给A.F 将记录(ID∗,T∗,σ∗) 插入列表L.

(4) A 提交Send(s,M) 询问.此时, s 是一个已激活的会话.F 首先验证消息 M 是否符合协议规范,以及 M 是否包含 speer的合法签名.如果验证不成功, 则返回 ⊥; 如果 s = s∗是创建的第 l 个会话, 且尚未完成, 如果 M 包含 ID∗对 T∗∗的合法签名 σ∗∗满足 (ID∗,T∗∗,σ∗∗)L, 则 F 直接输出 (ID∗,T∗∗,σ∗∗) 作为 ID-BBS 伪造签名.

(5) A 提交 Corrupt(ID) 询问.如果 ID = ID∗, 算法终止, 模拟失败; 如果 IDID∗, 且 ID 属于给定的 N 个用户, F 输出用户 ID 的长期私钥 skID, 否则返回 ⊥.

(6) A 提交 Ephemeral-key(s) 询问.如果 s 的临时密钥存在, 则返回 s 的临时密钥, 否则返回 ⊥.

(7) A 提交Session-key(s) 询问, F 按以下方式进行应答.

- 如果会话 s=s∗, 则算法终止, 模拟失败.

(8) 如果A 提交了 Test(s∗) 询问, 则算法终止, 模拟失败.

从模拟过程可以看出, 如果事件 E2发生 (模拟过程第 (4) 步), 则算法 F 成功完成 ID-BBS 签名挑战, 而在第 (5)、(7) 和 (8) 步则可能失败, 那么 F 成功的优势为从而可推导出

引理 2令其中, 事件 O 表示 Game 3 中 Test 会话存在原始会话, 那么有

证明:Game 3 中, 如果事件 E2发生则敌手 A 输出随机的 b ∈(0,1), 那么: |P(S3|E2)−1/2| =|1/2 −1/2| = 0; 如果事件 E2不发生, 则 Test 会话必然存在原始会话, 此时 A 成功的优势为

引理 3如果存在会话 s′是 Test 会话 s∗的原始会话, 且如果 Game 3 中存在敌手 A 以不可忽略的优势攻破协议 SIG(π) 的 ID-eCK-PFS 安全性, 那么可以构造算法 A′利用敌手 A 以不可忽略的优势攻破协议 π 的 ID-eCK 安全性, 且 A′成功的优势为

证明:考虑如下算法A′(以敌手A 作为子模块), 作为敌手, 从游戏游戏的构造可参考本文定理2) 中获得N 个用户身份和认证公钥.A′生成Game 3 的公开参数param 和所有N 个用户的签名密钥, 执行如下.

(1) 输入安全参数κ, 运行子算法A, 将公开参数param 以及 N 个用户的身份和公钥发送给A.

(2) A 提交Corrupt(ID) 询问.A′在中提交Corrupt(ID) 询问, 取得ID 的认证私钥,并组合其签名私钥返回给A.

(3) A 提交Ephemeral-key(s) 询问和Session-key(s) 询问, 则A′在中提交相应询问,并将得到的输出返回给A.

(4) A 提交 Send(s) 询问, 令sactor=IDi.A′按照下列方式作出应答.

- 如果A 提交Send(s,IDj) 询问以激活发起者会话s.则A′在中提交相同的询问, 以激活会话 s.A′得到输出 (IDi,Ri1,Ti).

- 如果 A 提交 Send(s,IDj,M) 询问以激活响应者会话 s.A′首先验证消息 M = (IDj,Rj1,Rj2,Rj3,Tj,σj) 是否符合协议规范, 以及 σj是否是 IDj对 Tj的合法签名, 如果验证不成功,则返回 ⊥.否则A′在中提交Send(s,IDj,M′) 询问, 其中, M′=(IDj,Rj1Tj),得到输出(IDi,Ri1,Ti).

- 如果 A 提交 Send(s,M) 询问.此时, s 是一个已激活的会话.A′首先验证消息 M 是否符合协议规范, 以及 M 是否包含 speer的合法签名.如果验证不成功, 则返回 ⊥; 否则 A′在中提交Send(s,M′) 询问, 其中, M′=(IDj,Rj1Tj).

- A′计算 IDi对 Ti的签名 σi, 将 (IDi,Ri1,Ri2,Ri3,Ti,σi) 返回给 A.

(5) A 提交Test(s∗) 询问, 则A′向提交Test(s∗) 询问, 并将得到的输出返回给A.

(6) 最后, A 输出其猜测 b′∈(0,1).如果不存在会话 s 是 Test 会话 s∗的原始会话, 那么 A′终止模拟, 模拟失败; 否则A′直接输出b′作为其对的猜测.

模拟过程中, 如果 A 破坏了ID-eCK-PFS 新鲜性, 那么 A′终止模拟, 模拟失败.

如果模拟成功完成,则存在会话s′是Test 会话s∗的原始会话,根据本文2.2.3 节的分析,此时Game 3 模拟表1 中的场景 S2、S3 和 S4, 而场景 S2 和 S3/S4 分别与 eCK 模型中的场景 S2′和 S1′等效.因此, 如果Game 3 成功完成,也必然成功完成.由模拟过程可知, 如果A 猜测成功, 则A′也成功, 显然 A′成功的优势为:那么:

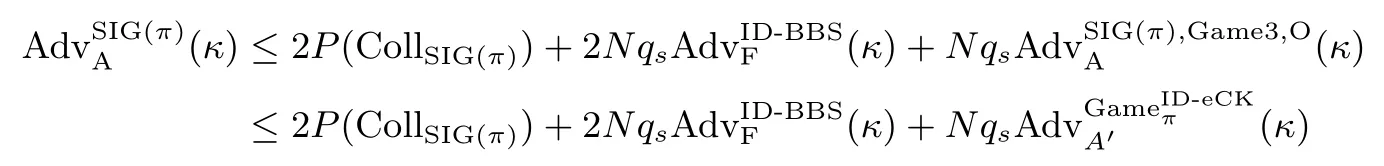
4.2 协议对比分析

表2 对几种前向安全的ID-AKA 协议进行了对比分析, 安全性方面列举了抗密钥泄露伪装(KCI)、临时密钥泄露抵抗(ESR) 和完美前向安全(PFS) 三个主要的安全属性, 计算开销方面主要列举了单个实体的双线性对运算 (用 P 表示)、模指数运算 (用E 表示) 和点乘运算 (用 M 表示) 次数.

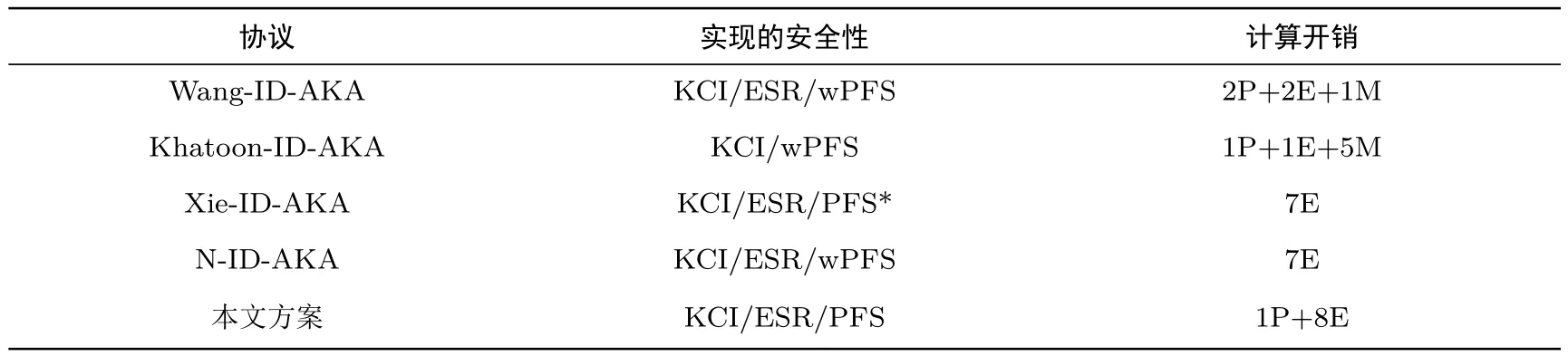
表2 相关ID-AKA 协议比较Table 2 Comparison of related ID-AKA protocols

安全性方面, N-ID-AKA 方案仅实现了弱的完美前向安全, 文献[10,19]虽然声称其提出的方案实现了完美前向安全, 但是其安全模型仅模拟被动的 wPFS 敌手, 安全性规约过程中, 在 Test 会话 s∗完成以前, 不允许敌手主动地向 s∗注入他所选定的临时秘密参数.事实上, Wang-ID-AKA 方案和Khatoon-ID-AKA 方案仅实现了弱的完美前向安全性.与本文方案相似, Xie-ID-AKA 方案采用了 Cremers 等人提出的 SIG 变换方法, 但是该方案没有给出完备的安全性证明.相比本文采用的 ID-BBS 签名机制,Xie-ID-AKA 方案采用的 Schnorr-like 签名存在两个弱点, 第一, Schnorr-like 签名仅实现了 EUF-CMA安全, 不满足SUF-CMA[25]安全性, 第二, 当签名采用的临时秘密泄露, 将导致长期认证私钥泄露.因此,Schnorr-like 算法并不满足 SIG 变换对签名算法的要求 (见文献 [24]定理 1).表2 中, 我们用 “PFS*” 表示Xie-ID-AKA 方案所实现的完美前向安全性.显然, PFS* 强于wPFS, 但弱于PFS.

从计算性能来看, Wang-ID-AKA 方案、N-ID-AKA 方案和Khatoon-ID-AKA 方案未使用签名算法,Xie-ID-AKA 方案采用Schnorr-like 签名算法, 具有较好的计算性能.本文方案的认证过程在N-ID-AKA方案的基础上进行了优化, 但是由于采用了强不可伪造签名, 总体计算开销仍稍高于其它4 种方案.进一步优化有赖于提出更高效、且具有SUF-CMA 安全性的基于身份签名机制.

5 结束语

本文提出一种强安全的 ID-AKA 协议, 在 eCK 安全的基础上进一步实现完美的前向安全性.本文首先对 Boneh 和 Boyen 提出的 BBS 签名方案进行改造, 提出基于身份的 ID-BBS 签名方案, 具有强不可伪造性; 然后, 以 N-ID-AKA 方案为基础进行简化, 降低计算开销, 采用 ID-BBS 算法对会话临时公钥进行签名, 提出具有更强安全性的 ID-AKA 方案.新方案能防止攻击者在密钥协商阶段注入由其选择的临时秘密信息, 实现了完美前向安全性.此外, 本文对比分析了 eCK-PFS 模型和 eCK 模型的主要区别, 结合 eCK-PFS 模型和 ID-eCK 模型, 定义了ID-AKA 方案分析的强安全模型 ID-eCK-PFS, 并基于ID-eCK-PFS 模型对本文提出方案的安全性进行了规约证明.对比分析表明, 本文提出的 ID-AKA 方案具有更强的安全性, 而计算开销也在可接受的范围之内.

在一轮隐式认证密钥交换协议基础上采用 SIG 变换能实现完美前向安全性, 且具有通用认证方案的优点, 使得协议设计更加灵活.但是, 签名算法的使用将隐式认证变为了显示认证, 且在一定程度上增加了原方案的计算开销.那么, 能实现完美前向安全性的一轮隐式认证密钥交换协议仍然是一个开放性的问题.