路基平衡湿度的分布规律及影响因素研究

覃宇丽 张亚芳

摘要：文章为分析不同因素对路基内部的平衡湿度分布和演化规律的影响，基于Darcy定律、Fick理论和Fourier扩散公式，采用VADOSE/W软件，模拟了15 a内长期气候条件下路基内部湿度平衡的动态变化过程，通过现场监测和规范计算评估了数值模拟结果的可靠性和准确性，并针对路堤高度、边坡坡度及地下水位三大影响因素，分析路基内部土体含水量随时间的演变规律，为路基的设计与施工提供理论依据和技术支持。

关键词：路基平衡湿度;路堤高度;边坡坡度;地下水位

0 引言

路基内部湿度的变化对路基的强度、水稳定性以及车辆荷载作用下的刚度都有显著的影响，具体表现为路基湿度过大会造成公路长期路用性能降低并损坏路基[1-2]。然而，路基湿度的变化是多因素共同作用的结果，例如：气候环境、路基断面形式、路基土质和地下水位等，路基湿度的预估方法与影响因素有割舍不开的联系[3-4]。因此，掌握长期气候作用下路基湿度平衡的分布规律及影响因素研究，能对在公路运营期间保证路基长期稳定性的设计和施工提供理论指导与技术支持。

路基湿度平衡测定常采用的方法有试验法和数值模拟法两种。在试验方面，Drumm[5]等通过现场含水率勘探试验，分析了路基的湿度状态及变化范围，总结出不同土质路基与水分迁移之间的变化关系;Perera[6]等通过长期的现场监测建立了不同土质的吸力与TMI之间的关系，并结合土水特征曲线预估路基土的含水率;杨果林[7]等通过不同地区路基土室内模型试验，在不同排水边界、不同压实条件下，分别模拟路基在晴天、积水、降雨等因素下路基土含水率变化规律。然而采用试验方法耗时长，难以检测长期气候作用下路基湿度平衡变化规律。近年来，基于湿度耦合理论的数值分析软件逐渐运用于气候条件下路基湿度平衡的研究，如Rajeev[8]等通过室内和现场试验确定路基内部土体的初始湿度及湿度平衡变化规律，并采用数值模拟的计算结果与现场试验数据结果进行对比，发现两者所得的数据结果吻合度较高;张锐[9]等模拟了广西10 a内气候变化条件下包盖膨胀土路堤湿度变化过程，并对其进行了数值模拟，分析了平衡湿度随吸力的变化规律，以及大气长期作用下物理处治膨胀土路堤的湿度平衡规律。

在公路建设和运营过程中，受长期自然气候条件影响，路基湿度场是一个不断变化的过程，路基湿度的影响因素复杂多变，不同因素对路基湿度平衡规律和湿度状态有何影响，是值得探讨的问题。为此，本文以广西百泮二级公路改扩建工程某黏土边坡为依托，采用数值模拟法对新建公路路基平衡湿度进行预估研究，分析路基长期湿度场演化规律，通过现场监测和规范计算对比评估路基内部湿度平衡分布规律的数值模拟结果，并探讨路堤高度、边坡坡度和地下水位对路基平衡湿度的影响。

1 湿热耦合计算理论

大气通过降雨和蒸发频繁地与路基内部和表面进行着水热交换，其产生的水热梯度驱使水、汽在路基内部迁移，从而改变路基的湿度状态。这一过程是湿热耦合的过程，可以采用非饱和土湿热耦合计算理论进行分析[10]。

非饱和土中液态水的流动遵循Darcy定律，水蒸气的扩散遵循Fick理论，热传导遵循Fourier扩散公式，因此，分别考虑液态水流动、平流过程中产生水蒸气扩散以及热传导的非饱和土的水热耦合的控制方程为：

基于上述湿热耦合理论就可以建立路基湿度数值计算方法，在长期气候条件下（降雨量、气温、相对湿度、风速等）对路基平衡湿度变化规律进行建模和计算。

2 路基平衡湿度的分布规律

2.1 数值模型的建立

根据广西百泮二级公路扩建工程某黏土边坡建设实际状况，通过现场调研选取数值计算的几何模型为：路堤高度为8 m，路堤顶面宽9 m，地基厚度为5 m。由于路基横断面为对称结构，因此为简化计算，选取路基中线右侧建立模型，并以A点作为分析特征点。路基计算模型和网格划分如图1所示。

为全面了解路基在建成通车多年后内部土体的平衡湿度，通过室内外试验获取路基土的基本物理力学指标、土水特性和渗透特性参数，对大气及地下水作用下的路基在路堤高度、边坡坡度和地下水位单因素变化情况下路基内部土体的路基平衡湿度分布规律进行探讨，设置如下三种数值模拟计算方案来对路基边坡内部土体平衡湿度的变化规律进行模拟。主要数值模拟方案如表1所示。

通过气象站获得该地区2016—2017年全年的降雨量、风速、气温、相對湿度等气象数据的变化曲线如图2所示。为研究长期气候作用下路基湿度平衡演化规律，假定计算周期为15 a，并假设每年的气象变化一致。

2.2 路基平衡湿度变化规律

路基内部湿度在气候条件的长期作用下变化比较明显，下页图3为15 a内路基内部饱和度的变化云图。初始状态时，路基内部的饱和度相对较低，且湿度分布比较均匀。经过1 a的气候以及地下水的影响，此时路基内部的整体饱和度较初始状态时有了一定程度的提高，路面结构层以下的路基土饱和度从上到下逐渐升高，且在边坡表层一定深度内的路基土饱和度比路基内部饱和度低。3 a后，路基内部的饱和度仍然在变化，并逐步趋于稳定。经观察5 a后和15 a后的湿度场变化情况不难发现，路基内部土体的饱和度基本上不再受到气候条件及地下水作用的影响，饱和度已经趋于稳定，这说明湿度的变化经历快速上升、缓慢增加和湿度平衡三个阶段，3～5 a内路基内部的湿度达到了平衡状态。当路基内部的湿度达到平衡状态时，路基土体的整体饱和度会比初始状态时的整体饱和度有所提高，降雨入渗和地下水位的升高使路基土的湿度增加。同时，越接近地下水位线，土体的饱和度越高，地下水位变化对路基内部湿度的影响要强于降雨入渗对路基湿度的影响。

2.3 路基湿度预估比对

[JP3]布设距地下水位不同高程的5个观测点，以现场监测测点的质量含水率，以及计算规范预估[11]的饱和度为研究对象，与数值模型结果进行路基平衡湿度的变化规律的预估比对，结果见表2。数值模拟计算所得的路基湿度值在规范预估值的范围内，与范围值相差不到5%，满足规范计算精度。模拟计算所得值与现场监测的数据相差不大，说明了采用数值模拟预估15 a内湿度平衡变化规律具有较高的准确性和可靠性。

3 路基平衡湿度影响因素分析

3.1 路堤高度对路基平衡湿度的影响

由图4可知，当路堤高度分别为5 m、8 m和10 m时，路基分别运营3.16 a、4.15 a和5.38 a后内部A点处湿度分别达到平衡状态。因此可以看出，路基高度不同，内部点达到湿度平衡状态的时间也不相同，即路基高度越高，路基内部点达到湿度平衡状态所用的时间越长;路基高度越低，内部测试点达到湿度平衡状态所需时间也就越短，且不同路基高度下的A点平衡湿度是一致的。当路基高度增加后，路基内部土体达到平衡湿度时地下水位上升高度也增加。[JP4]因为，在路基边坡坡度保持一定的情况下，提高路基高度，路基边坡坡长相应变长，在相同时间内，大气降雨和蒸发等自然因素对路基内部土体湿度的影响越大，降雨入渗的雨水不断补给上升的毛细水，且在降雨入渗条件下，坡脚处积水迅速地渗入到路基中，进而导致地下水上升。

3.2 边坡坡度对路基平衡湿度的影响

路基边坡坡度不同，路基内部土体达到湿度平衡状态所需时间不同。如图5所示，坡度为1∶1.75时，路基内部达到湿度平衡状态所需的时间最短，坡度1∶1.5次之，坡度1∶1最长。换言之，路基边坡坡度越缓，路基内部达到湿度平衡状态所需的时间越短;坡度越陡，路基内部达到湿度平衡状态所需时间越长，且对土样含水量的影响也就越大。坡度为1∶1.75时A点平衡湿度为37.7%，坡度为1∶1.5时A点平衡湿度为37.6%，坡度为1∶1时A点平衡湿度为37.5%，路基边坡坡度对平衡湿度影响不大，只对平衡时间有影响。这是因为路基边坡坡度越缓，坡面受大气降雨影响的入渗面越大，且大气降雨在坡面的停滞时间越长，从而使缓坡在大气降雨过程中所积累的水分较陡坡更多。其次，在气候因素的影响下，缓坡坡面受温度、风速等作用的面积较大，其路基土体温度上升也比陡坡明显。

3.3 地下水位对路基平衡湿度的影响

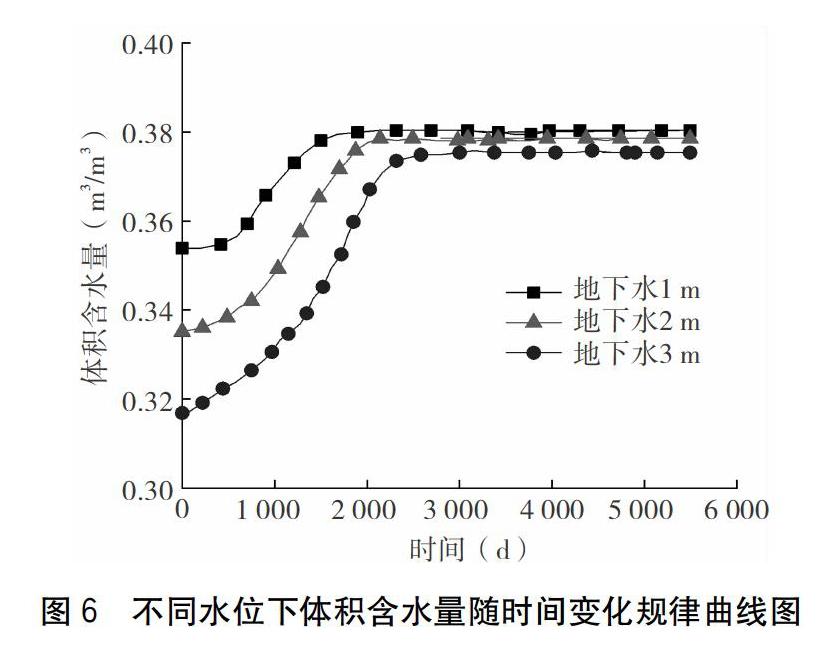
如图6所示，随着时间的推移，A点体积含水量逐渐增加，当增加到一定含水量时将趋于稳定状态，且A点越接近地下水位，增长趋势就越明显。初始地下水位不同，路基内部土体达到平衡状态所需的时间也不相同，初始地下水位越高，路基内部土体达到湿度平衡状态所需的时间越短，初始地下水位越低，路基内部土体达到湿度平衡状态所需的时间越长。地下水位越高，A点平衡湿度越大，地下水位越低，A点平衡湿度越小，即B2点平衡湿度：地下水1 m>地下水2 m>地下水3 m。这是由于地下水在毛细作用的影响下进入路基，使路基土含水量增大直至达到平衡状态。初始地下水位不同，路基土毛细作用上升到路基内部同一层位所需时间不同，越接近初始地下水位，各测点路基土毛细作用上升到同一层位所需时间越短，且达到该层位的路径也越短，否则相反。路基填土均为非饱和土，路基土毛细作用主要来自非饱和土的基质吸力的作用，在毛细作用的影响下，地下水向路基内部迁移，缩短了毛细作用的路径，路基内部土体湿度逐渐增加，可以看出，地下水位上升和下降对毛细作用有着显著的影响。

4 结语

（1）受长期气候因素的影响，路基整体湿度随降雨入渗和地下水位抬高而增加，湿度的变化经历快速上升、缓慢增加和湿度平衡三个阶段，3～5 a内路基内部的湿度达到了平衡状态。当路基内部的湿度达到平衡状态时，路基土体的整体饱和度会比初始状态时的整体饱和度有所提高。数值模拟计算所得的路基湿度与规范计算和现场监测的平衡湿度接近。

（2）[JP3]路基高度越高，路基内部点达到湿度平衡状态所用的时间越长，路基高度越低，达到湿度平衡状态所需时间越短。路基高度不同，中心点平衡湿度相同。[JP2]

（3）边坡坡度越小，达到湿度平衡状态所需的时间越短，坡度越大，达到湿度平衡状态所需的时间越长，且对土样含水量的影响越大。路基坡度对内部土体平衡湿度影响不大。

（4）初始地下水位不同，路基内部土体达到平衡状态所需的时间不相同，初始地下水位越高，其达到湿度平衡状态所需的时间越短，平衡湿度越大。

参考文献：

[1]王中文，龙志东，陈 杰，等. 花岗岩残积土路基边坡水毁模拟分析[J]. 交通科学与工程，2016，32（4）：10-15.

[2]姚永胜，张军辉，李 崛，等. 江西省昌樟高速公路改扩建工程老路基渗水处治方法研究[J]. 中外公路，2018，38（3）：14-18.

[3]蒋红光，曹 让，马晓燕，等. 考虑路基平衡湿度状态的黄泛区中高液限黏土抗剪强度研究[J]. 岩石力学与工程学报，2018，37（12）：2 819-2 828.

[4]张 玉，冉武平，李 爽.强蒸发地区受路面覆盖效应的路基温湿度场表达[J]. 科学技术与工程，2019，19（23）：239-245.

[5]Drumm E C，Meier R. LTPP data analysis：daily and seasonal variations in insitu material properties[M]. Washington：Transportation Research Board，National Research Council，2003.

[6]Perera Y Y，Zapata C E，Houston S L，et al. Moisture equilibria beneath highway pavements[C]. 83rd Annual Meeting of Transportation Research Board，2004. [LL]

[7]杨果林，刘义虎. 膨胀土路基含水量在不同氣候条件下的变化规律模型试验研究[J]. 岩石力学与工程学报，2005，24（24）：4 524-4 533.

[8]Rajeev P，Chan D，Kodikara J. Ground–atmosphere interaction modelling for long-term prediction of soil moisture and temperature[J]. Canadian Geotechnical Journal，2012，49（9）：1 059-1 073.

[9]张 锐，郑健龙. 公路膨胀土路堤湿度平衡规律研究[J]. 公路交通科技，2013，30（11）：24-32. [ZK）]

[10]熊 义，高 抗. 蒸发条件下非饱和土水分迁移的数值模拟[J]. 三峡大学学报（自然科学版），2014，36（1）：46-50.