高三复习专题——概率统计解答题

梁丽怡

(佛山市第三中学 广东佛山 528000)

关于概率统计的专题复习，高水平的学校更多的是放手让学生刷题，因为本身内容难度不大，但是随着阅读量的增大，动辄几百字的文章让人云里雾里，加之繁杂的计算，这些都是失分的原因。针对以上两大问题，笔者在今年备考中，对概率统计这一部分中常失分的两类题型作了以下分析：

一、决策问题

在此类型问题中，阅读量较大，涉及社会的各项措施，和实际生活联系紧密，具有重要的应用意义。决策问题实际是在不同的情况下进行分析计算，实际上就是分段函数，通过分段计算从而达到利益最大或者损耗最小的目的，实际应用性很强。这也是学生最陌生、最无从下手的类型。

例（2016 全国1 文18）：

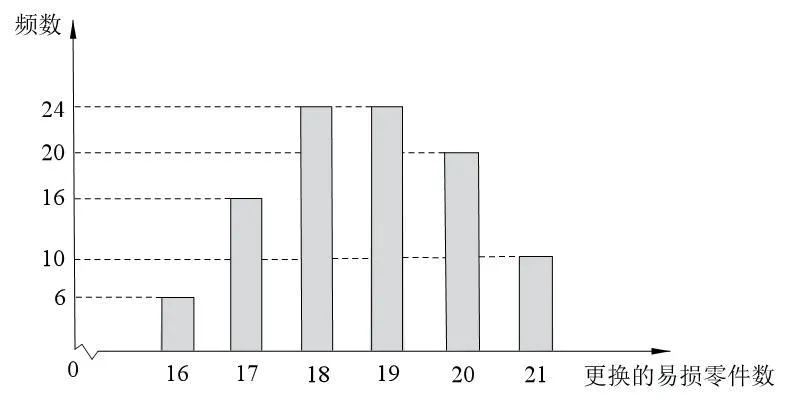
某公司计划购买1台机器，该种机器使用三年后即被淘汰。机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元。在机器使用期间，如果备件不足再购买，则每个500元。现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元，n表示购机的同时购买的易损零件数）

（I）若n=19，求y与x的函数解析式；

（II）若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；

（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？

解：（Ⅰ）当x ≤1 9 时，y=3 8 0 0；当x ＞1 9 时，y=3800+500(x-19)=500x-5700，所以y与x的函数解析式为

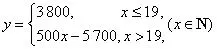
（Ⅱ）由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故n的最小值为19。

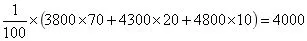
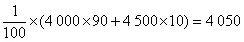
学生在阅读时受到x，y，n多个自变量的影响，搞不清楚x，y之间是分段函数的关系。此时先让学生在“现需决策在购买机器时应同时购买几个易损零件”这句话中体会到是决策问题，分段的原因是买多了备件可能会造成浪费，但买少了却需要更高的单价购买零件。那么应当是根据三年使用期内需更换的易损零件数的调查结果计算所需费用的平均数，比较大小后便可做出决策。第（1）问中n=19，则x≤19是费用就只是原件和备件的总和；如果x＞19，则需要增加另外购买的易损零件数的费用，而购买数目是x-19。其实这也是商家的常用促销手段，比如说商品的售后期随着费用增长而延长。教学时多举例，才能让学生体会到概率统计是和实际生活密不可分的。

二、线性回归问题（非线性回归问题）

回归问题往往要计算回归直线的斜率和截距，为了简化计算，条件会有参考数据，但可能有些是与题目无关的，这就需要学生在运算中注意等价代换，尤其是非线性回归问题有换元这步，更要注意这点。

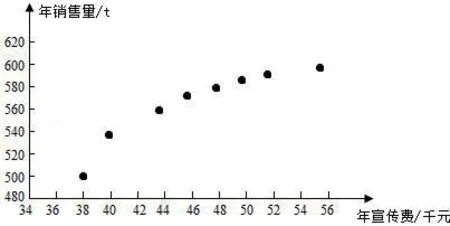
例：某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费xi（单位：千元）对年销售量yi（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值。

?

（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；附：对于一组数据（u1v1），（u2v2）…（unvn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：

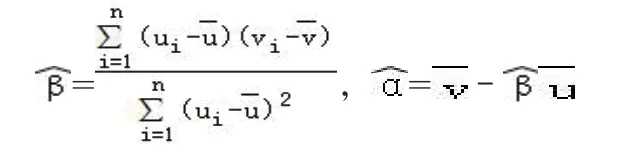
（Ⅱ）对于非线性拟合问题，先作出散点图，再根据散点图选择合适的函数类型，设出回归方程，利用换元法将非线性回归方程化为线性回归方程，求出样本数据换元后的值，然后根据线性回归方程的计算方法计算变换后的线性回归方程系数，即可求出非线性回归方程，关键在于换元的正确与否。

在第二问中，我们只需要找到对应变量进行换元，便可以轻松代入参考数据。因为题目和对应的公式间需要转化的字母有四对，所以学生公式代入时会比较混乱。可以用图示表达v=y，c=α，u=，β=d，这样每一步转化都会很清晰。