基于PSO-SVM的来水量预测模型

王龙强

（河北省水利水电第二勘测设计研究院，石家庄 050021）

降水、气温、径流等多种因子具有很大的不确定性，并影响着中长期的水文预报情况。来水量在年际间具有较大的随机性和不确定性，在影响来水量的众多因素之间也存在着复杂关系，众多因素之间的相互作用关系很难利用常规方法进行比较准确的表达。本文通过来水量模型的建立，利用某河45年的径流资料对来年来水量进行预测，并与实际值进行比较。

1 来水量SVM模型

来水量预测模型是反应影响来水量的因素与来水量之间的关系。本文采用用于非线性建模与预测的支持向量回归机模型。

以来水量预测模型为例，模型训练输入为影响因素。由影响因素对应的来水量得到一组输入信号：来水量数据集（X，Y），即：

式中 xi∈Rn为输入向量；yi∈Rn为与xi相对应的输出向量；N为数据点总数。

通过输入向量与输出向量的点集进行函数回归［1］，如式（2）：

式中 y为输出向量；x为输入向量；w，b为函数常数项。

假设在ε精度，所有训练样本可用线性拟合函数表示，如式（3）：

式中 ε 为精度；其他字母含义同上。

优化目标是最小化‖w‖2/2。由于允许误差，引入松弛变量ξ≥0和≥0，如式（4）：

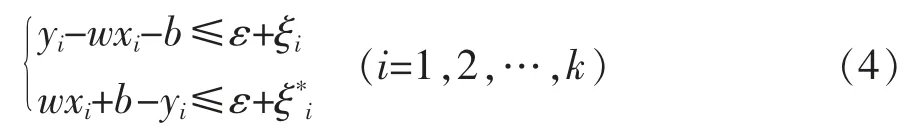
W（α，α*）最大时，由此得到支持向量机的拟合函数［2］f（x），如式（6）：

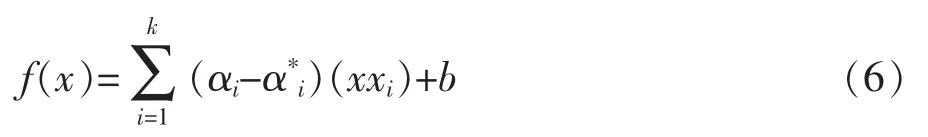
式中 W（α，α*）为目标函数；C为大于零的常数；αi，为Lagrange乘子，αi，将只有小部分不为0，对应的样本即为支持向量；其他字母含义同上。

考虑到非线性问题可通过变换将问题映射到某个高维的特征空间进行求解。用核函数可代替线性问题的内积运算，即K（xi，xj）=φ（xi）φ（xj）。由此，式（5）变换如式（7）：

式中 字母含义同上。

那么式（6）拟合函数可变换如式（8）：

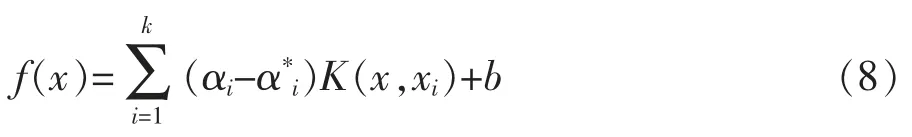
式中 K（x，xi）为核函数；其他字母含义同上。

本文所用为径向基型，如式（9）：

式中 σ 为核函数的宽度；其他字母含义同上。

以上为来水量预测的LS-SVM模型。

2 基于PSO的来水量模型SVM参数优化

粒子群优化算法PSO，是在人类对鸟类捕食时行为研究的基础上得到的一种进化计算方法。由于粒子群算法容易实现且不需要调整过多参数因而被广泛应用于多种领域。

采用某河流45年径流资料对模型进行实例验证，根据水库前期径流资料预测未来年份的来水量。

模型数据从资料的样本集中选取45个数据，其中25个数据作为训练样本，10个数据作为校验样本数据，剩余10个数据作为测试样本数据。设粒子群规模为45，SVM参数C的取值范围 ［0.1，104］，σ 的取值范围［10-3，10］，设最大迭代次数Gmax为500，加速因子c1为0.01，c2为0.01。目标函数为训练样本集和校验样本集的均方差之和为最小，经过PSO优化选择得到使得目标函数最小的最优解C为2816，σ 为1.27。适应度值的迭代优化过程如图1。

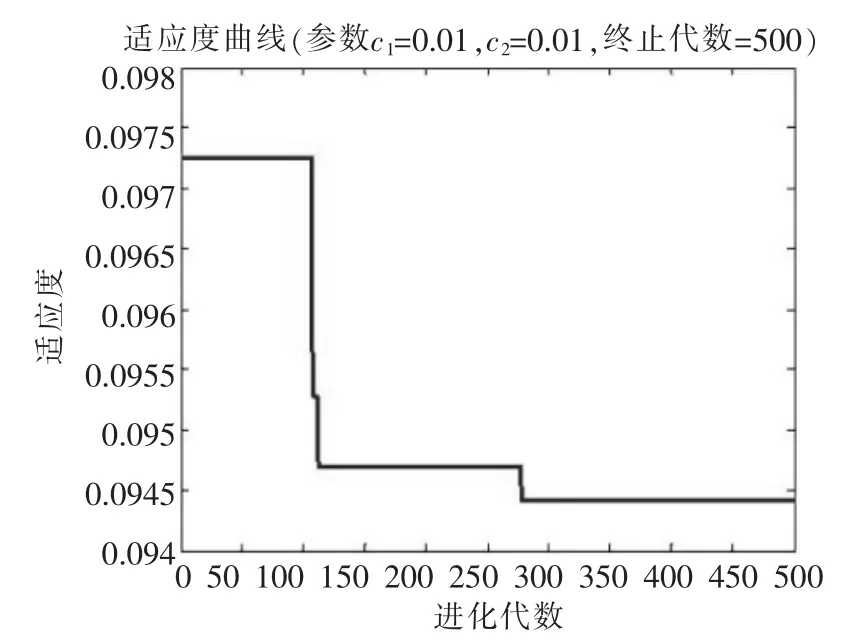
图1 适应度函数进化过程

由图1可见，在100代左右快速收敛，275代左右达到最优值。在最优参数的基础上，模型对10个测试样本数据进行测试，所得预测模型如图2。

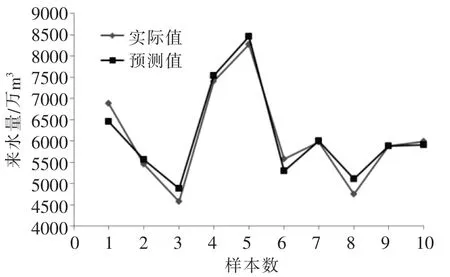
图2 PSO-SVM预测模型

将模型所得预测值与实际值进行比较，所得误差结果如表1。

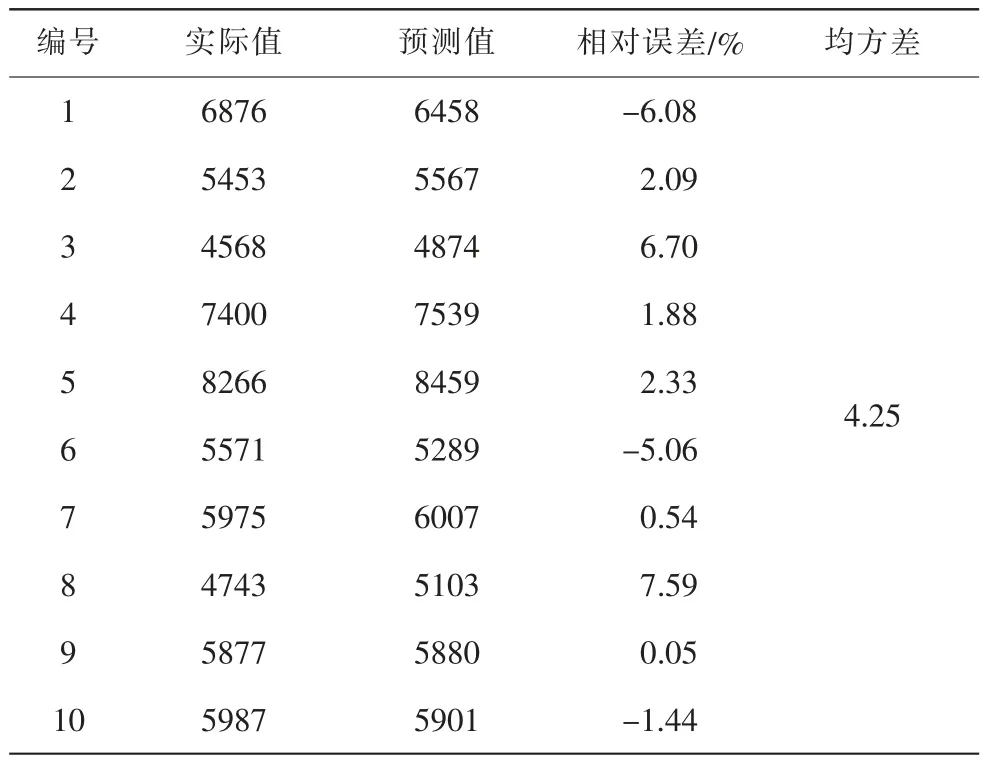
表1 PSO-SVM预测结果

实际值与预测值的相对误差绝对值最大值7.59，最小值0.05，均方差4.25。

3 模型比较

本文用相同数据建立BP神经网络模型与PSOSVM模型数据进行比较，BP神经网络预测模型［3］如图3，预测值与实际值的比较如表2。

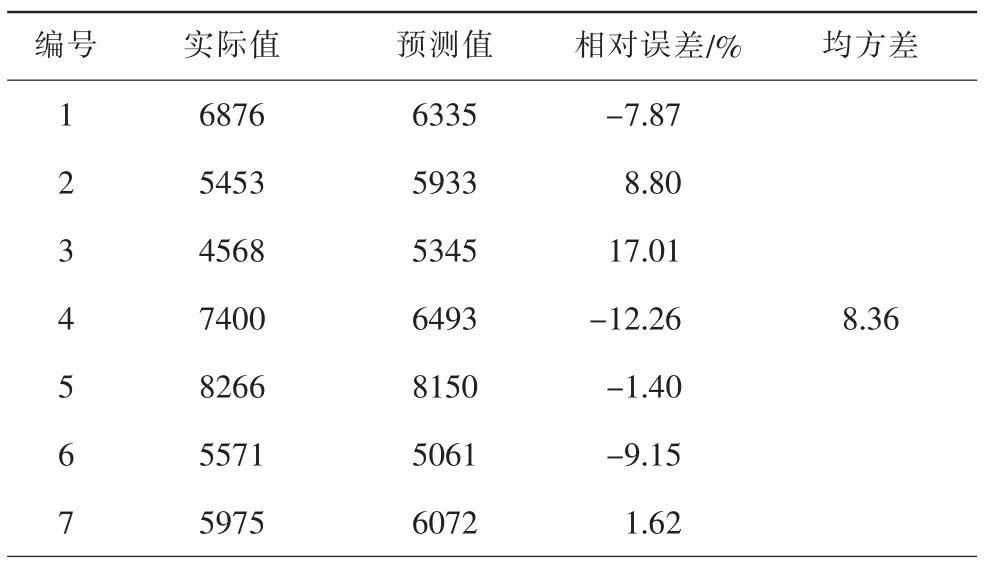
表2 BP神经网络预测结果

续表2

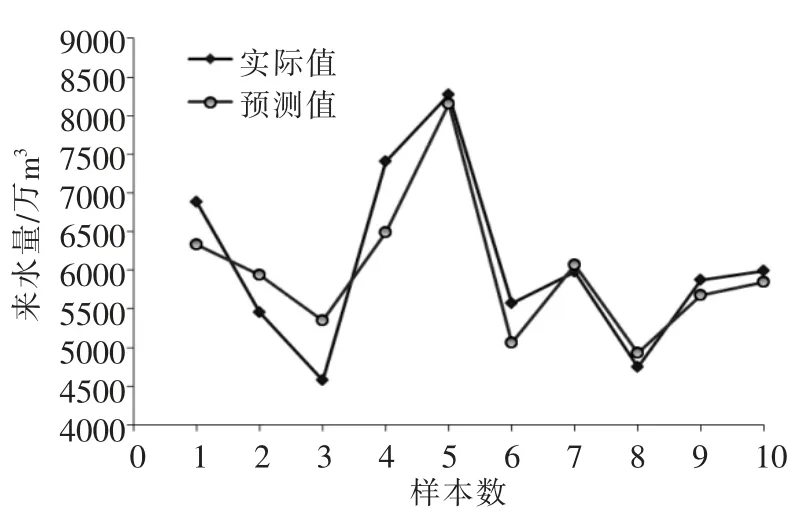
图3 BP神经网络预测模型

BP神经网络模型所得预测值与实际值相对误差的绝对值最大17.01%，最小1.40%，均方差8.36。

从两种模型的预测曲线拟合程度来看，PSOSVM模型拟合程度明显好于BP神经网络模型；从表中的数据分析结果来看，PSO-SVM模型的预测值与实际值的误差的均方差小于BP神经网络预测模型值；PSO-SVM模型对来水量的预测精度更高。

4 结语

建立了来水量PSO-SVM模型，并利用样本数据进行了训练与预测，并利用BP神经网络模型对同一组数据进行了预测，模型数据结果分析表明：PSOSVM模型预测值与实际值的均方差小于BP神经网络，PSO-SVM对预测曲线的拟合程度高于BP神经网络。PSO-SVM模型能够为来水量的预测提供更为精准的参考依据。